平面及其基本性质26张PPT
图片预览






文档简介
课件26张PPT。问题1:观察图片中的房屋,有你熟悉的空间几何体吗? 2.1.1平面及其基本性质问题2:(1)生活中有哪些例子给了我们直线形象? (2)直线有哪些基本特征?直线的特征:①直的;②向两边无
线延伸;③无粗细. (3)怎么表示直线?图形语言:
符号语言:直线AB,或者直线a.你认为,什么是平面?AB平面的基本特征:平的、很平的面平面 几何里的“平面”是由生活中的课桌面、
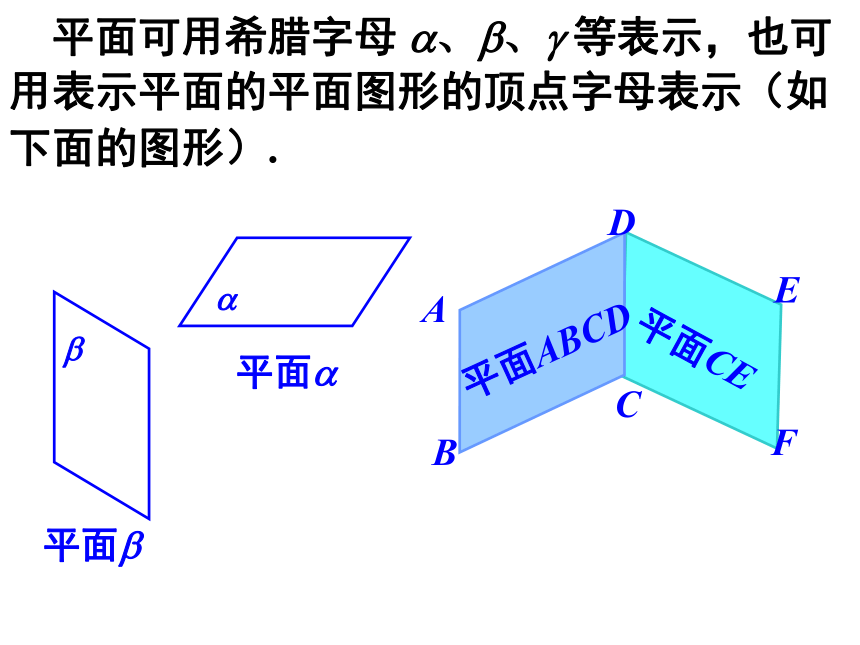
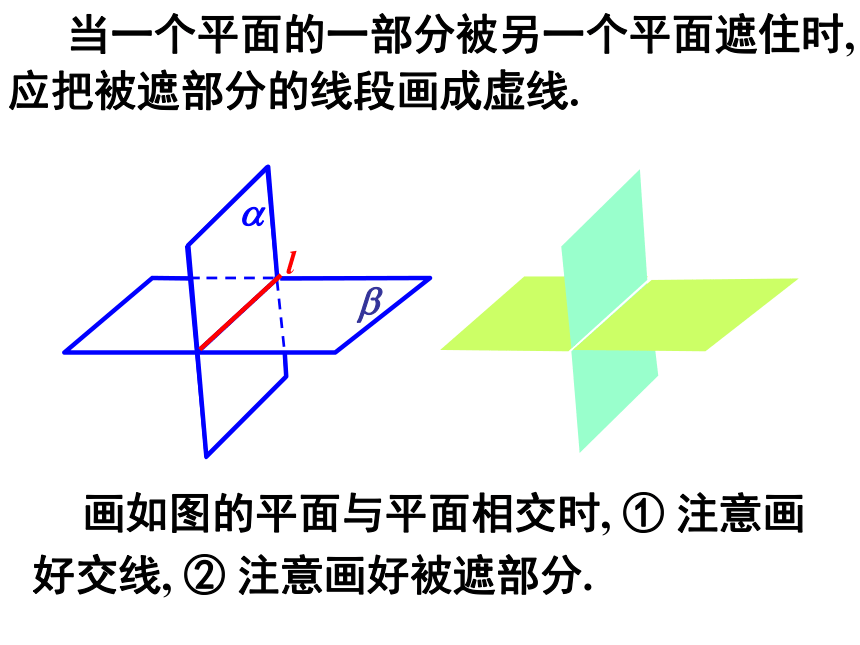
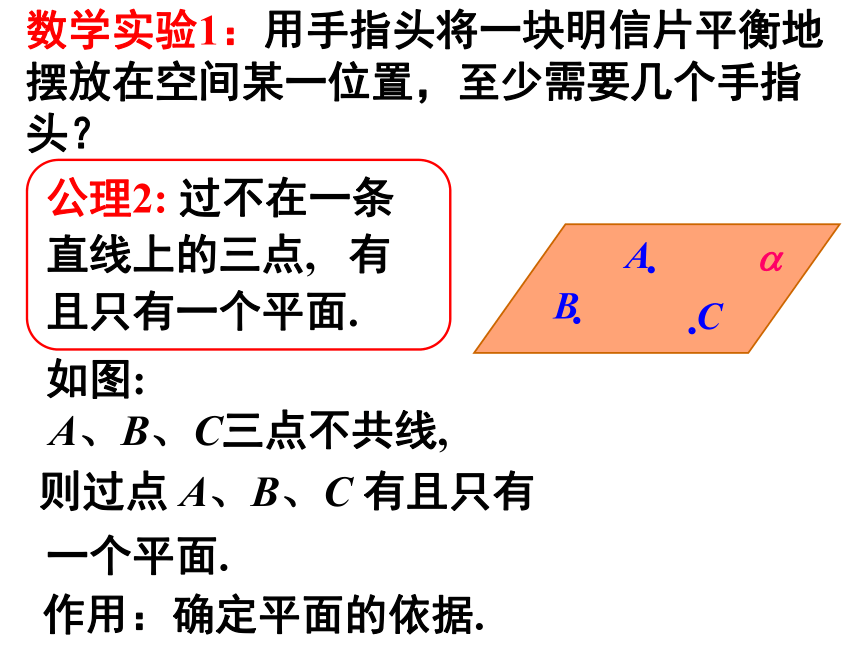
黑板面、海面等等抽象出来的数学概念.无限延展的、没有厚薄的.如何在纸上画图形表示平面呢?通常,用平行四边形来表示平面. 平面也可用其他平面图形,如用三角形、梯形等来表示平面.平面a平面bbaABCDEF 平面可用希腊字母 a、b、g 等表示,也可用表示平面的平面图形的顶点字母表示(如下面的图形).平面ABCD平面CE 当一个平面的一部分被另一个平面遮住时, 应把被遮部分的线段画成虚线. 画如图的平面与平面相交时, ① 注意画好交线, ② 注意画好被遮部分.abl数学实验1:用手指头将一块明信片平衡地摆放在空间某一位置,至少需要几个手指头?公理2: 过不在一条直线上的三点, 有且只有一个平面.如图:A、B、C三点不共线,则过点 A、B、C 有且只有一个平面.作用:确定平面的依据. 数学实验2:如果把明信片看作一个平面,把你的笔看作是一条直线的话:
(1)你能使笔上的一个点在平面内,而其他点不在平面内吗?
(2)你能使笔上的两个点在平面内,而其他点不在平面内吗?公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.a●●AB用数学符号如何表示?点动成___线线动成___面 思考.如图,在长方体 ABCD-A?B?C?D? 中,用符号表示下列点、直线、平面之间的位置关系.
(1)点A 平面ABCD ;
(2)点A? 平面ABCD ;
(3)直线AB 平面ABCD;
(4)直线A?A 平面ABCD;
公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.作用:判断直线是否在平面内.a●●AB如图:A∈l ,B∈l ,A∈a ,B∈a ,? l ? a .直线的“无限延展性”平面的“无限延展性”直线的“直”平面的“平”桌面平整吗?数学实验3:把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?
公理3 如果两个不重合的平面有一个公共
点,那么它们有且只有一条过该点的公共直线.●ablP公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.P?a∩b? a∩b = l, 且 P?l.作用:判断点在直线上.A.B例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.例2 空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,已知EH和FG相交于点P。
求证:P点在直线BD上。 P 练习: 判断下列命题是否正确, 正确的在括号内划“√”, 错误的划 “×”.
(1) 平面 a 与平面 b 相交, 它们只有有限
个公共点. ( )
(2)三点确定一个平面. ( )
(3) 经过两条相交直线有且只有一个平面.
( )
(4) 经过一条直线和这条直线外一点, 有且只有一个平面. ( )
课堂小结知识方法思想通过本节课的学习,你有哪些收获? 课后作业
必做:
(1) P43练习:1,2,4
(2) P51习题2.1A组:1,2
选做:如图是一个正方体表面的展开图, 如果将它还原为正方体, 那么 AB, CD, EF, GH 这四条直线相互是什么位置关系?
平面的数学史
线延伸;③无粗细. (3)怎么表示直线?图形语言:
符号语言:直线AB,或者直线a.你认为,什么是平面?AB平面的基本特征:平的、很平的面平面 几何里的“平面”是由生活中的课桌面、
黑板面、海面等等抽象出来的数学概念.无限延展的、没有厚薄的.如何在纸上画图形表示平面呢?通常,用平行四边形来表示平面. 平面也可用其他平面图形,如用三角形、梯形等来表示平面.平面a平面bbaABCDEF 平面可用希腊字母 a、b、g 等表示,也可用表示平面的平面图形的顶点字母表示(如下面的图形).平面ABCD平面CE 当一个平面的一部分被另一个平面遮住时, 应把被遮部分的线段画成虚线. 画如图的平面与平面相交时, ① 注意画好交线, ② 注意画好被遮部分.abl数学实验1:用手指头将一块明信片平衡地摆放在空间某一位置,至少需要几个手指头?公理2: 过不在一条直线上的三点, 有且只有一个平面.如图:A、B、C三点不共线,则过点 A、B、C 有且只有一个平面.作用:确定平面的依据. 数学实验2:如果把明信片看作一个平面,把你的笔看作是一条直线的话:
(1)你能使笔上的一个点在平面内,而其他点不在平面内吗?
(2)你能使笔上的两个点在平面内,而其他点不在平面内吗?公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.a●●AB用数学符号如何表示?点动成___线线动成___面 思考.如图,在长方体 ABCD-A?B?C?D? 中,用符号表示下列点、直线、平面之间的位置关系.
(1)点A 平面ABCD ;
(2)点A? 平面ABCD ;
(3)直线AB 平面ABCD;
(4)直线A?A 平面ABCD;
公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.作用:判断直线是否在平面内.a●●AB如图:A∈l ,B∈l ,A∈a ,B∈a ,? l ? a .直线的“无限延展性”平面的“无限延展性”直线的“直”平面的“平”桌面平整吗?数学实验3:把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?
公理3 如果两个不重合的平面有一个公共
点,那么它们有且只有一条过该点的公共直线.●ablP公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.P?a∩b? a∩b = l, 且 P?l.作用:判断点在直线上.A.B例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.例2 空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,已知EH和FG相交于点P。
求证:P点在直线BD上。 P 练习: 判断下列命题是否正确, 正确的在括号内划“√”, 错误的划 “×”.
(1) 平面 a 与平面 b 相交, 它们只有有限
个公共点. ( )
(2)三点确定一个平面. ( )
(3) 经过两条相交直线有且只有一个平面.
( )
(4) 经过一条直线和这条直线外一点, 有且只有一个平面. ( )
课堂小结知识方法思想通过本节课的学习,你有哪些收获? 课后作业
必做:
(1) P43练习:1,2,4
(2) P51习题2.1A组:1,2
选做:如图是一个正方体表面的展开图, 如果将它还原为正方体, 那么 AB, CD, EF, GH 这四条直线相互是什么位置关系?
平面的数学史
