1.1 菱形的性质与判定同步练习(含解析)
文档属性
| 名称 | 1.1 菱形的性质与判定同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 459.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-31 22:20:29 | ||
图片预览


文档简介
1.1 菱形的性质和判定练习题(含解析)
一、单选题
1.下列命题正确的是(?? )
A.对角线相等的四边形是平行四边形 B.对角线相等的四边形是矩形 C.对角线互相垂直的平行四边形是菱形 D.对角线互相垂直且相等的四边形是正方形
2.如图,已知菱形ABCD的边长等于2,若∠DAB=60°,则对角线BD的长为(?? )
A.?1??????????????????????????????????????B.???????????????????????????????????????C.?2?????????????????????????????????????D.?
3.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是(??? )。
A.20 B.24 C.40 D.48
4.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是(?? )。
A.????????? ? ???B.?2????????? ???? ??????C.??????????????? ????????????D.?4
5.若菱形 的周长是16, ∠A=60° ,则对角线 的长度为( )
A.?2?????????????? ?????????B.?????? ??????????????????C.?4?????????????? ????????D.?
6.如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱
形ABCD的周长为(?? )
A.?24???????????????????? ?????????B.?18???????? ?????????????????C.?12??????????? ???????????D.?9
7.菱形 的两条对角线长分别为 和 ,则它的周长和面积分别为(? ? )
A.?? ???????????? ?????B.?? ???? ????C.?? ????????? ???????D.??
8.如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF,则下列结论正确的是( ??)
A.?AB= EF?????? ?B.?AB=2EF???????? ????C.?AB= EF?? ?????D.?AB= EF
9.如图,在菱形ABCD中,AC=6 ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( ??)
A.?6????????? ???? ?B.?3 ??????????????????? ???????C.?2 ??? ???????????D.?4.5
二、填空题
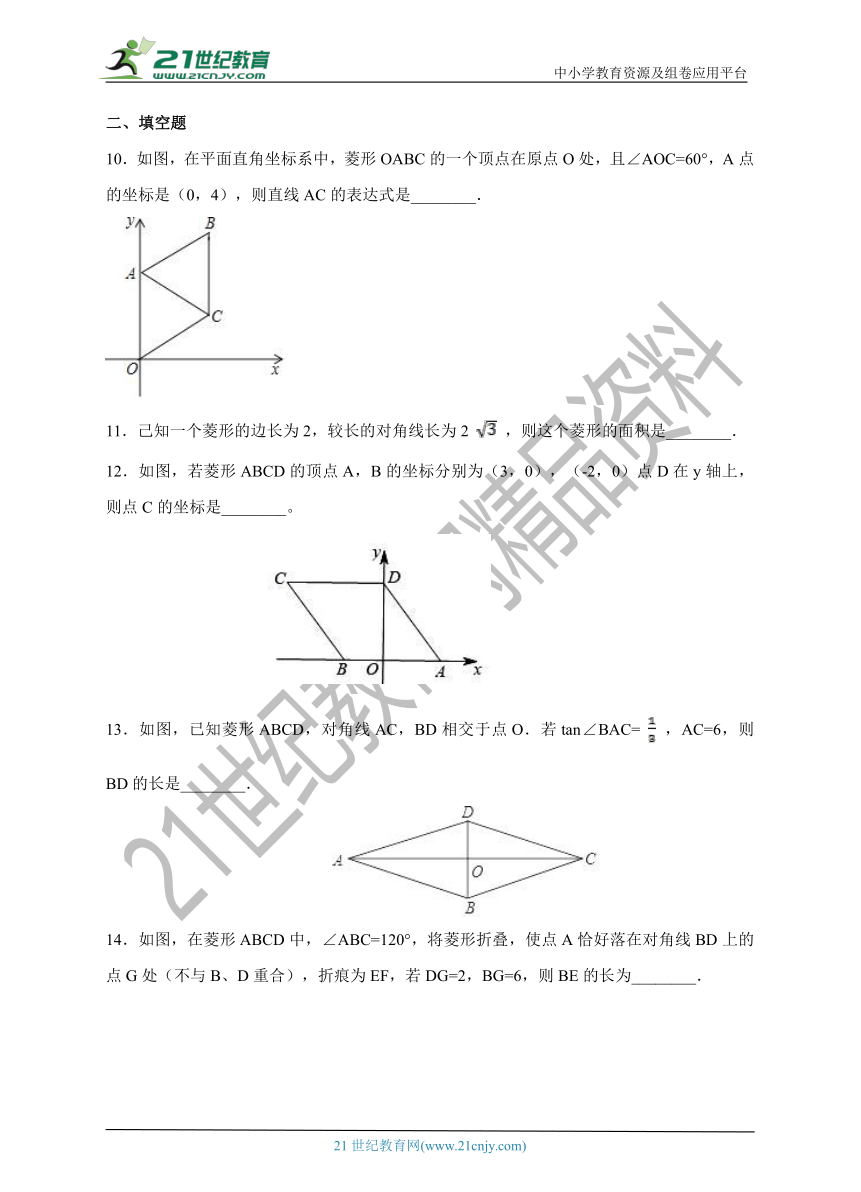
10.如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,A点的坐标是(0,4),则直线AC的表达式是________.
11.己知一个菱形的边长为2,较长的对角线长为2 ,则这个菱形的面积是________.
12.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0)点D在y轴上,则点C的坐标是________。
13.如图,已知菱形ABCD,对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是________.
14.如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为________.
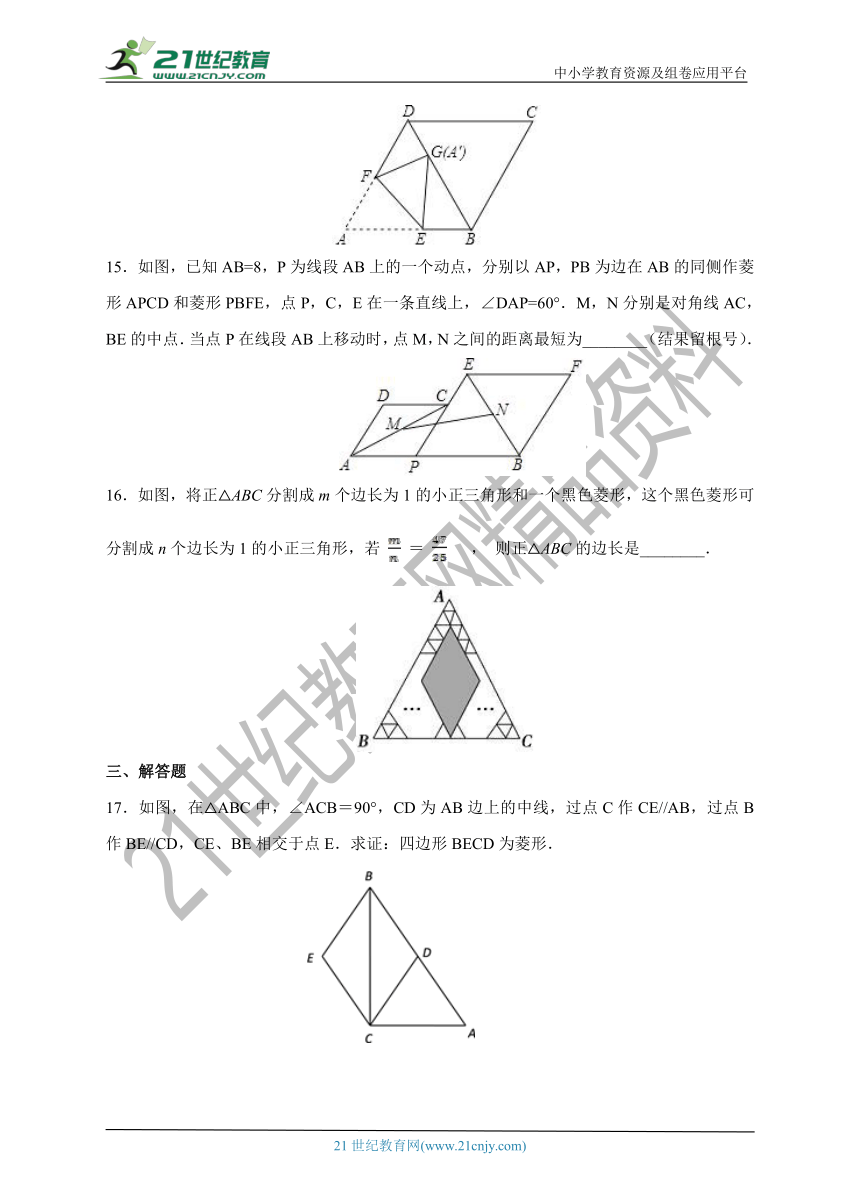
15.如图,已知AB=8,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE的中点.当点P在线段AB上移动时,点M,N之间的距离最短为________(结果留根号).
16.如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小正三角形,若 = , 则正△ABC的边长是________.
三、解答题
17.如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点C作CE//AB,过点B作BE//CD,CE、BE相交于点E.求证:四边形BECD为菱形.
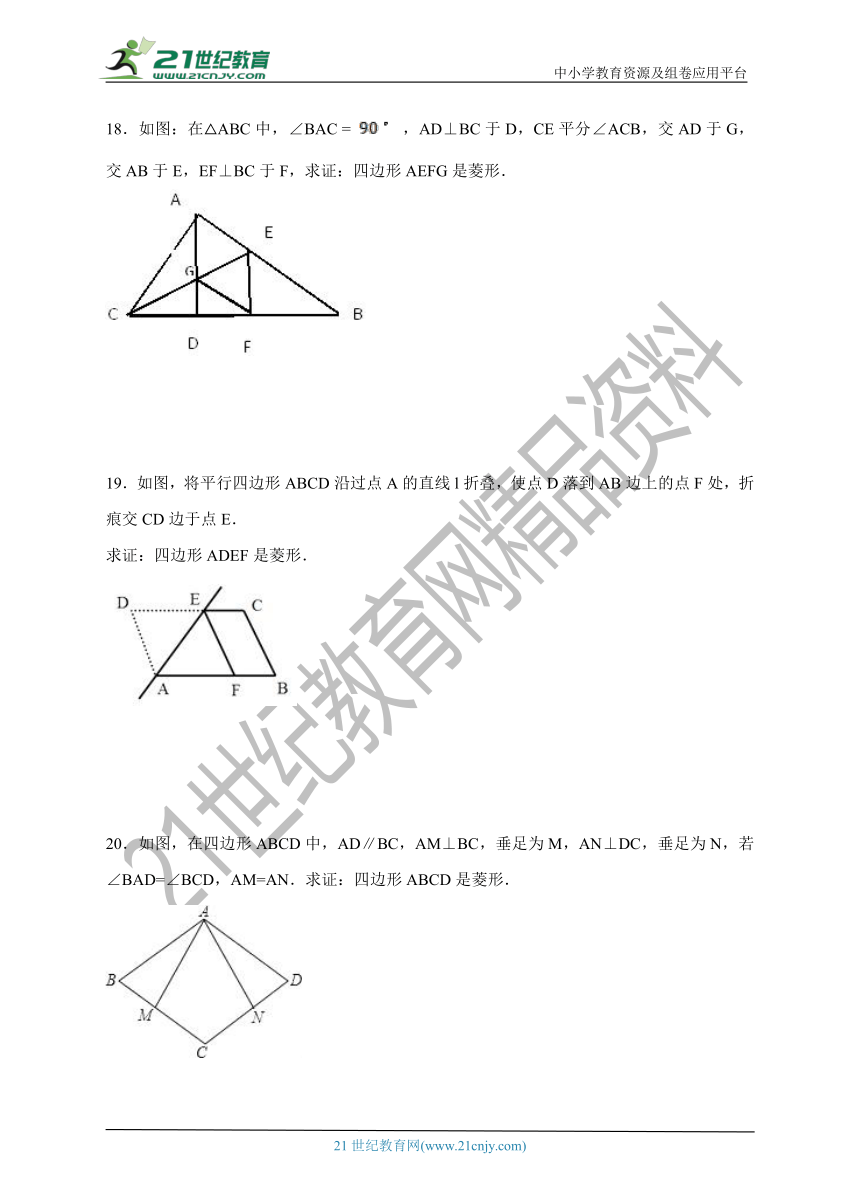
18.如图:在△ABC中,∠BAC = ,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
19.如图,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点F处,折痕交CD边于点E. 求证:四边形ADEF是菱形.
20.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN.求证:四边形ABCD是菱形.
21.如图,△ABC≌△ABD,点E在边AB上,并且CE∥BD,连接DE. 求证:四边形BCED是菱形.
22.如图,已知四边形ABCD是菱形,DE⊥AB,DF⊥BC,求证:△ADE≌△CDF. ?
23.如图,在?ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.
答案解析部分
一、单选题
1.【答案】C
【解析】A.改成为:对角线“互相平分”的四边形是平行四边形,故A不符合题意;B.改成为:对角线相等的“平行四边形”是矩形,故B不符合题意; C.正确,故C符合题意; D.改成为:对角线互相垂直且相等的“平行四边形”是正方形,故D不符合题意; 故答案为:C.
2.【答案】C
【解析】∵菱形ABCD的边长为2,∴AD=AB=2,又∵∠DAB=60°, ∴△DAB是等边三角形,∴AD=BD=AB=2,则对角线BD的长是2. 故答案为:C.
3.【答案】A
【解析】设对角线AC、BC交于点O,
∵四边形ABCD是菱形,AC=6,BD=8 ∴A0=3,BO=4,AC⊥BC,∴AB=5,∴C菱形ABCD=4×5=20. 故答案为:A.
4.【答案】A
【解析】∵菱形ABCD的周长为16,∴菱形ABCD的边长为4, ∵∠BAD=60°, ∴△ABD是等边三角形, 又∵O是菱形对角线AC、BD的交点, ∴AC⊥BD, 在Rt△AOD中, ∴AO= , ∴AC=2A0=4 , ∴S△ACD= ·OD·AC= ×2×4 =4 , 又∵O、E分别是中点, ∴OE∥AD, ∴△COE∽△CAD, ∴ , ∴ , ∴S△COE= S△CAD= ×4 = . 故答案为:A.
5.【答案】C
【解析】∵菱形ABCD的周长是16, ∴AB=AD=CD=BC=4, ∵∠A=60°, ∴△ABD是等边三角形, ∴AB=AD=BD=4. ∴对角线BD的长度为4. 故答案为:C.
6.【答案】A
【解析】∵E是AC中点, ∵EF∥BC,交AB于点F, ∴EF是△ABC的中位线, ∴BC=2EF=2×3=6, ∴菱形ABCD的周长是4×6=24, 故答案为:A.
7.【答案】B
【解析】∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,AB=BC=CD=AD, ∵AC=8cm,BD=6cm,∴AD=5cm,周长=4×5=20 cm, S菱形ABCD= AC?BD=24cm2 . 故答案为:B.
8.【答案】D
【解析】连接AC、BD交于点O, ∵四边形ABCD是菱形,∴OA= AC,OB= BD,AC⊥BD, ∵E、F、G、H分别是边AB、BC、CD和DA的中点, ∴EH= BD,EF= AC, ∵EH=2EF, ∴OA=EF,OB=2OA=2EF, 在Rt△AOB中,AB= = EF, 故答案为:D.
9.【答案】C
【解析】如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P, 则点P、M即为使PE+PM取得最小值的点, 则有PE+PM=PE′+PM=E′M, ∵四边形ABCD是菱形, ∴点E′在CD上, ∵AC=6 ,BD=6, ∴AB= , 由S菱形ABCD= AC?BD=AB?E′M得 ×6 ×6=3 ?E′M, 解得:E′M=2 , 即PE+PM的最小值是2 , 故答案为:C.
二、填空题
10.【答案】
【解析】如图, 由菱形OABC的一个顶点在原点O处,A点的坐标是(0,4),得OC=OA=4, 又∵∠1=60°, ∴∠2=30°, sin∠2= , ∴CD=2, cos∠2=cos30°= , OD=2 , ∴C(2 ,2), 设AC的解析式为y=kx+b, 将A,C点坐标代入函数解析式,得 , 解得 , 直线AC的表达式是y=﹣ x+4, 故答案为:y=﹣ x+4. 11.【答案】
【解析】依照题意画出图形,如图所示. 在Rt△AOB中,AB=2,OB= , ∴OA= =1, ∴AC=2OA=2, ∴S菱形ABCD= AC?BD= ×2×2 =2 . 故答案为:2 .
12.【答案】(-5,4)
【解析】∵A(3,0),B(-2,0), ∴AB=5,AO=3,BO=2, 又∵四边形ABCD为菱形, ∴AD=CD=BC=AB=5, 在Rt△AOD中, ∴OD=4, 作CE⊥x轴, ∴四边形OECD为矩形, ∴CE=OD=4,OE=CD=5, ∴C(-5,4). 故答案为:(-5,4).
13.【答案】2
【解析】∵四边形ABCD是菱形,AC=6,∴AC⊥BD,OA= AC=3,BD=2OB. 在Rt△OAB中,∵∠AOD=90°, ∴tan∠BAC= , ∴OB=1, ∴BD=2. 故答案为2.
14.【答案】2.8
【解析】作EH⊥BD于H, 由折叠的性质可知,EG=EA, 由题意得,BD=DG+BG=8, ∵四边形ABCD是菱形, ∴AD=AB,∠ABD=∠CBD= ∠ABC=60°, ∴△ABD为等边三角形, ∴AB=BD=8, 设BE=x,则EG=AE=8﹣x, 在Rt△EHB中,BH= x,EH= x, 在Rt△EHG中,EG2=EH2+GH2 , 即(8﹣x)2=( x)2+(6﹣x)2 , 解得,x=2.8,即BE=2.8, 故答案为:2.8.
15.【答案】2
【解析】连接PM、PN. ∵四边形APCD,四边形PBFE是菱形,∠DAP=60°, ∴∠APC=120°,∠EPB=60°, ∵M,N分别是对角线AC,BE的中点, ∴∠CPM= ∠APC=60°,∠EPN= ∠EPB=30°, ∴∠MPN=60°+30°=90°, 设PA=2a,则PB=8﹣2a,PM=a,PN= (4﹣a), ∴MN= = = , ∴a=3时,MN有最小值,最小值为2 , 故答案为2 .
16.【答案】12
【解析】设正△ABC的边长为x , 则高为 x , S△ABC= x· x= x2.∵所分成的都是正三角形,∴结合图形可得黑色菱形的较长的对角线为 x- , 较短的对角线为( x- ) = x-1, ∴黑色菱形的面积= (x-2)2 , ∴ = = , 整理得,11x2-144x+144=0,解得x1= (不符合题意,舍去),x2=12.∴△ABC的边长是12. 答案:12
三、解答题
17.【答案】证明:∵CE//AB,BE//CD, ∴四边形BECD是平行四边形. 又∵∠ACB=90°,CD为AB边上的中线, ∴CD= AB. 又∵CD为AB边上的中线 ∴BD= AB. ∴BD=CD. ∴平行四边形BECD是菱形
【解析】由平行四边形的定义可得四边形BECD是平行四边形,再证得一组邻边相等即可得解;由直角三角形斜边上的中线等于斜边的一半可得BD=CD,则根据有一组邻边相等的平行四边形是菱形可得平行四边形BECD是菱形。
18.【答案】证明:∵AD⊥BC, ∴∠ADB=90°, ∵∠BAC=90°, ∴∠B+∠BAD=90°,∠BAD+∠CAD=90°, ∴∠B=∠CAD, ∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA), ∴AE=EF(角平分线上的点到角两边的距离相等), ∵CE=CE,∴由勾股定理得:AC=CF, ∵△ACG和△FCG中 ? ∴△ACG≌△FCG, ∴∠CAD=∠CFG, ∵∠B=∠CAD ∴∠B=∠CFG, ∴GF∥AB, ∵AD⊥BC,EF⊥BC, ∴AD∥EF, 即AG∥EF,AE∥GF, ∴四边形AEFG是平行四边形, ∵AE=EF, ∴平行四边形AEFG是菱形.
【解析】由已知用边角边易证△ACG≌△FCG,可得∠CAD=∠CFG,结合已知条件易得∠B=∠CFG,由平行线的判定可得GF∥AB,根据同垂直于一条直线的两条直线互相平行可得AD∥EF,由两组对边分别平行的四边形是平行四边形可得四边形AEFG是平行四边形,再根据有一组邻边相等的平行四边形是菱形可得平行四边形AEFG是菱形.
19.【答案】证明:由折叠可知,DE=EF,AD=AF,∠DEA=∠FEA ∵四边形ABCD是平行四边形 ∴DE∥AF ∴∠DEA=∠EAF ∴∠EAF=∠FEA ∴AF=EF???? ∴AF=AD=DE=EF ∴四边形ADEF是菱形.
【解析】由折叠的性质和平行四边形的性质易证AF=AD=DE=EF,根据有四条边相等的四边形是菱形可得四边形ADEF是菱形。
20.【答案】证明:∵AD∥BC, ∴ , ? ∵∠BAD=∠BCD, ∴∠B=∠D, ∴四边形ABCD是平行四边形, ∵AM⊥BC,AN⊥DC, ∴ ? 在△ABM和△ADN中, ? ∴△ABM≌△ADN(AAS), ∴AB=AD, ∴四边形ABCD是菱形.
【解析】由题意易证两组对角相等的四边形是平行四边形可得四边形ABCD是平行四边形,结合已知用角角边易证△ABM≌△ADN,则可得AB=AD,由一组邻边相等的平行四边形是菱形可得四边形ABCD是菱形。
21.【答案】证明:∵ ≌ , ∴ ?, 在 和 中 , ∴ ≌ ?, ∴ , 又∵ , ∴ ?, ∴ , ∴ , ∴ , ∴四边形BCED是菱形.
【解析】由ΔABC≌ΔABD可得BC=BD,∠1=∠2 ,用边角边可证ΔBEC≌ΔBED,则CE=DE,根据平行线的性质易证CE=CB,于是有CE=CB=DB=DE,由四边都相等的四边形是菱形可得四边形BCED是菱形.
22.【答案】证明:∵四边形ABCD是菱形,∴∠A=∠C,AD=CD, 又∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°, 在△ADE和△CDF中, ,∴△ADE≌△CDF(AAS).
【解析】先利用菱形的性质可求出∠A=∠C,AD=CD,再结合已知条件DE⊥AB,DF⊥BC,可得∠AED=∠CFD,从而由AAS可证△ADE≌△CDF。
23.【答案】解:∵在?ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO, 在△EOD和△FOB中, , ∴△DOE≌△BOF(ASA),∴OE=OF,
又∵OB=OD,∴四边形EBFD是平行四边形, ∵EF⊥BD,∴四边形BFDE为菱形
【解析】根据平行四边形的性质,得出BO=DO,∠EDB=∠FBO,再利用ASA证明△DOE≌△BOF,得出OE=OF,就可证得四边形EBFD是平行四边形,然后根据对角线互相垂直的平行四边形是菱形,即可得证。
1.1 菱形的性质和判定练习题(含解析)
一、单选题
1.下列命题正确的是(?? )
A.对角线相等的四边形是平行四边形 B.对角线相等的四边形是矩形 C.对角线互相垂直的平行四边形是菱形 D.对角线互相垂直且相等的四边形是正方形
2.如图,已知菱形ABCD的边长等于2,若∠DAB=60°,则对角线BD的长为(?? )
A.?1??????????????????????????????????????B.???????????????????????????????????????C.?2?????????????????????????????????????D.?
3.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是(??? )。
A.20 B.24 C.40 D.48
4.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是(?? )。
A.????????? ? ???B.?2????????? ???? ??????C.??????????????? ????????????D.?4
5.若菱形 的周长是16, ∠A=60° ,则对角线 的长度为( )
A.?2?????????????? ?????????B.?????? ??????????????????C.?4?????????????? ????????D.?
6.如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱
形ABCD的周长为(?? )
A.?24???????????????????? ?????????B.?18???????? ?????????????????C.?12??????????? ???????????D.?9
7.菱形 的两条对角线长分别为 和 ,则它的周长和面积分别为(? ? )
A.?? ???????????? ?????B.?? ???? ????C.?? ????????? ???????D.??
8.如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF,则下列结论正确的是( ??)
A.?AB= EF?????? ?B.?AB=2EF???????? ????C.?AB= EF?? ?????D.?AB= EF
9.如图,在菱形ABCD中,AC=6 ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( ??)
A.?6????????? ???? ?B.?3 ??????????????????? ???????C.?2 ??? ???????????D.?4.5
二、填空题
10.如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,A点的坐标是(0,4),则直线AC的表达式是________.
11.己知一个菱形的边长为2,较长的对角线长为2 ,则这个菱形的面积是________.
12.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0)点D在y轴上,则点C的坐标是________。
13.如图,已知菱形ABCD,对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是________.
14.如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为________.
15.如图,已知AB=8,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE的中点.当点P在线段AB上移动时,点M,N之间的距离最短为________(结果留根号).
16.如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小正三角形,若 = , 则正△ABC的边长是________.
三、解答题
17.如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点C作CE//AB,过点B作BE//CD,CE、BE相交于点E.求证:四边形BECD为菱形.
18.如图:在△ABC中,∠BAC = ,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
19.如图,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点F处,折痕交CD边于点E. 求证:四边形ADEF是菱形.
20.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN.求证:四边形ABCD是菱形.
21.如图,△ABC≌△ABD,点E在边AB上,并且CE∥BD,连接DE. 求证:四边形BCED是菱形.
22.如图,已知四边形ABCD是菱形,DE⊥AB,DF⊥BC,求证:△ADE≌△CDF. ?
23.如图,在?ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.
答案解析部分
一、单选题
1.【答案】C
【解析】A.改成为:对角线“互相平分”的四边形是平行四边形,故A不符合题意;B.改成为:对角线相等的“平行四边形”是矩形,故B不符合题意; C.正确,故C符合题意; D.改成为:对角线互相垂直且相等的“平行四边形”是正方形,故D不符合题意; 故答案为:C.
2.【答案】C
【解析】∵菱形ABCD的边长为2,∴AD=AB=2,又∵∠DAB=60°, ∴△DAB是等边三角形,∴AD=BD=AB=2,则对角线BD的长是2. 故答案为:C.
3.【答案】A
【解析】设对角线AC、BC交于点O,
∵四边形ABCD是菱形,AC=6,BD=8 ∴A0=3,BO=4,AC⊥BC,∴AB=5,∴C菱形ABCD=4×5=20. 故答案为:A.
4.【答案】A
【解析】∵菱形ABCD的周长为16,∴菱形ABCD的边长为4, ∵∠BAD=60°, ∴△ABD是等边三角形, 又∵O是菱形对角线AC、BD的交点, ∴AC⊥BD, 在Rt△AOD中, ∴AO= , ∴AC=2A0=4 , ∴S△ACD= ·OD·AC= ×2×4 =4 , 又∵O、E分别是中点, ∴OE∥AD, ∴△COE∽△CAD, ∴ , ∴ , ∴S△COE= S△CAD= ×4 = . 故答案为:A.
5.【答案】C
【解析】∵菱形ABCD的周长是16, ∴AB=AD=CD=BC=4, ∵∠A=60°, ∴△ABD是等边三角形, ∴AB=AD=BD=4. ∴对角线BD的长度为4. 故答案为:C.
6.【答案】A
【解析】∵E是AC中点, ∵EF∥BC,交AB于点F, ∴EF是△ABC的中位线, ∴BC=2EF=2×3=6, ∴菱形ABCD的周长是4×6=24, 故答案为:A.
7.【答案】B
【解析】∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,AB=BC=CD=AD, ∵AC=8cm,BD=6cm,∴AD=5cm,周长=4×5=20 cm, S菱形ABCD= AC?BD=24cm2 . 故答案为:B.
8.【答案】D
【解析】连接AC、BD交于点O, ∵四边形ABCD是菱形,∴OA= AC,OB= BD,AC⊥BD, ∵E、F、G、H分别是边AB、BC、CD和DA的中点, ∴EH= BD,EF= AC, ∵EH=2EF, ∴OA=EF,OB=2OA=2EF, 在Rt△AOB中,AB= = EF, 故答案为:D.
9.【答案】C
【解析】如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P, 则点P、M即为使PE+PM取得最小值的点, 则有PE+PM=PE′+PM=E′M, ∵四边形ABCD是菱形, ∴点E′在CD上, ∵AC=6 ,BD=6, ∴AB= , 由S菱形ABCD= AC?BD=AB?E′M得 ×6 ×6=3 ?E′M, 解得:E′M=2 , 即PE+PM的最小值是2 , 故答案为:C.
二、填空题
10.【答案】
【解析】如图, 由菱形OABC的一个顶点在原点O处,A点的坐标是(0,4),得OC=OA=4, 又∵∠1=60°, ∴∠2=30°, sin∠2= , ∴CD=2, cos∠2=cos30°= , OD=2 , ∴C(2 ,2), 设AC的解析式为y=kx+b, 将A,C点坐标代入函数解析式,得 , 解得 , 直线AC的表达式是y=﹣ x+4, 故答案为:y=﹣ x+4. 11.【答案】
【解析】依照题意画出图形,如图所示. 在Rt△AOB中,AB=2,OB= , ∴OA= =1, ∴AC=2OA=2, ∴S菱形ABCD= AC?BD= ×2×2 =2 . 故答案为:2 .
12.【答案】(-5,4)
【解析】∵A(3,0),B(-2,0), ∴AB=5,AO=3,BO=2, 又∵四边形ABCD为菱形, ∴AD=CD=BC=AB=5, 在Rt△AOD中, ∴OD=4, 作CE⊥x轴, ∴四边形OECD为矩形, ∴CE=OD=4,OE=CD=5, ∴C(-5,4). 故答案为:(-5,4).
13.【答案】2
【解析】∵四边形ABCD是菱形,AC=6,∴AC⊥BD,OA= AC=3,BD=2OB. 在Rt△OAB中,∵∠AOD=90°, ∴tan∠BAC= , ∴OB=1, ∴BD=2. 故答案为2.
14.【答案】2.8
【解析】作EH⊥BD于H, 由折叠的性质可知,EG=EA, 由题意得,BD=DG+BG=8, ∵四边形ABCD是菱形, ∴AD=AB,∠ABD=∠CBD= ∠ABC=60°, ∴△ABD为等边三角形, ∴AB=BD=8, 设BE=x,则EG=AE=8﹣x, 在Rt△EHB中,BH= x,EH= x, 在Rt△EHG中,EG2=EH2+GH2 , 即(8﹣x)2=( x)2+(6﹣x)2 , 解得,x=2.8,即BE=2.8, 故答案为:2.8.
15.【答案】2
【解析】连接PM、PN. ∵四边形APCD,四边形PBFE是菱形,∠DAP=60°, ∴∠APC=120°,∠EPB=60°, ∵M,N分别是对角线AC,BE的中点, ∴∠CPM= ∠APC=60°,∠EPN= ∠EPB=30°, ∴∠MPN=60°+30°=90°, 设PA=2a,则PB=8﹣2a,PM=a,PN= (4﹣a), ∴MN= = = , ∴a=3时,MN有最小值,最小值为2 , 故答案为2 .
16.【答案】12
【解析】设正△ABC的边长为x , 则高为 x , S△ABC= x· x= x2.∵所分成的都是正三角形,∴结合图形可得黑色菱形的较长的对角线为 x- , 较短的对角线为( x- ) = x-1, ∴黑色菱形的面积= (x-2)2 , ∴ = = , 整理得,11x2-144x+144=0,解得x1= (不符合题意,舍去),x2=12.∴△ABC的边长是12. 答案:12
三、解答题
17.【答案】证明:∵CE//AB,BE//CD, ∴四边形BECD是平行四边形. 又∵∠ACB=90°,CD为AB边上的中线, ∴CD= AB. 又∵CD为AB边上的中线 ∴BD= AB. ∴BD=CD. ∴平行四边形BECD是菱形
【解析】由平行四边形的定义可得四边形BECD是平行四边形,再证得一组邻边相等即可得解;由直角三角形斜边上的中线等于斜边的一半可得BD=CD,则根据有一组邻边相等的平行四边形是菱形可得平行四边形BECD是菱形。
18.【答案】证明:∵AD⊥BC, ∴∠ADB=90°, ∵∠BAC=90°, ∴∠B+∠BAD=90°,∠BAD+∠CAD=90°, ∴∠B=∠CAD, ∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA), ∴AE=EF(角平分线上的点到角两边的距离相等), ∵CE=CE,∴由勾股定理得:AC=CF, ∵△ACG和△FCG中 ? ∴△ACG≌△FCG, ∴∠CAD=∠CFG, ∵∠B=∠CAD ∴∠B=∠CFG, ∴GF∥AB, ∵AD⊥BC,EF⊥BC, ∴AD∥EF, 即AG∥EF,AE∥GF, ∴四边形AEFG是平行四边形, ∵AE=EF, ∴平行四边形AEFG是菱形.
【解析】由已知用边角边易证△ACG≌△FCG,可得∠CAD=∠CFG,结合已知条件易得∠B=∠CFG,由平行线的判定可得GF∥AB,根据同垂直于一条直线的两条直线互相平行可得AD∥EF,由两组对边分别平行的四边形是平行四边形可得四边形AEFG是平行四边形,再根据有一组邻边相等的平行四边形是菱形可得平行四边形AEFG是菱形.
19.【答案】证明:由折叠可知,DE=EF,AD=AF,∠DEA=∠FEA ∵四边形ABCD是平行四边形 ∴DE∥AF ∴∠DEA=∠EAF ∴∠EAF=∠FEA ∴AF=EF???? ∴AF=AD=DE=EF ∴四边形ADEF是菱形.
【解析】由折叠的性质和平行四边形的性质易证AF=AD=DE=EF,根据有四条边相等的四边形是菱形可得四边形ADEF是菱形。
20.【答案】证明:∵AD∥BC, ∴ , ? ∵∠BAD=∠BCD, ∴∠B=∠D, ∴四边形ABCD是平行四边形, ∵AM⊥BC,AN⊥DC, ∴ ? 在△ABM和△ADN中, ? ∴△ABM≌△ADN(AAS), ∴AB=AD, ∴四边形ABCD是菱形.
【解析】由题意易证两组对角相等的四边形是平行四边形可得四边形ABCD是平行四边形,结合已知用角角边易证△ABM≌△ADN,则可得AB=AD,由一组邻边相等的平行四边形是菱形可得四边形ABCD是菱形。
21.【答案】证明:∵ ≌ , ∴ ?, 在 和 中 , ∴ ≌ ?, ∴ , 又∵ , ∴ ?, ∴ , ∴ , ∴ , ∴四边形BCED是菱形.
【解析】由ΔABC≌ΔABD可得BC=BD,∠1=∠2 ,用边角边可证ΔBEC≌ΔBED,则CE=DE,根据平行线的性质易证CE=CB,于是有CE=CB=DB=DE,由四边都相等的四边形是菱形可得四边形BCED是菱形.
22.【答案】证明:∵四边形ABCD是菱形,∴∠A=∠C,AD=CD, 又∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°, 在△ADE和△CDF中, ,∴△ADE≌△CDF(AAS).
【解析】先利用菱形的性质可求出∠A=∠C,AD=CD,再结合已知条件DE⊥AB,DF⊥BC,可得∠AED=∠CFD,从而由AAS可证△ADE≌△CDF。
23.【答案】解:∵在?ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO, 在△EOD和△FOB中, , ∴△DOE≌△BOF(ASA),∴OE=OF,
又∵OB=OD,∴四边形EBFD是平行四边形, ∵EF⊥BD,∴四边形BFDE为菱形
【解析】根据平行四边形的性质,得出BO=DO,∠EDB=∠FBO,再利用ASA证明△DOE≌△BOF,得出OE=OF,就可证得四边形EBFD是平行四边形,然后根据对角线互相垂直的平行四边形是菱形,即可得证。
一、单选题
1.下列命题正确的是(?? )
A.对角线相等的四边形是平行四边形 B.对角线相等的四边形是矩形 C.对角线互相垂直的平行四边形是菱形 D.对角线互相垂直且相等的四边形是正方形
2.如图,已知菱形ABCD的边长等于2,若∠DAB=60°,则对角线BD的长为(?? )
A.?1??????????????????????????????????????B.???????????????????????????????????????C.?2?????????????????????????????????????D.?
3.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是(??? )。
A.20 B.24 C.40 D.48
4.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是(?? )。
A.????????? ? ???B.?2????????? ???? ??????C.??????????????? ????????????D.?4
5.若菱形 的周长是16, ∠A=60° ,则对角线 的长度为( )
A.?2?????????????? ?????????B.?????? ??????????????????C.?4?????????????? ????????D.?
6.如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱
形ABCD的周长为(?? )
A.?24???????????????????? ?????????B.?18???????? ?????????????????C.?12??????????? ???????????D.?9
7.菱形 的两条对角线长分别为 和 ,则它的周长和面积分别为(? ? )
A.?? ???????????? ?????B.?? ???? ????C.?? ????????? ???????D.??
8.如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF,则下列结论正确的是( ??)
A.?AB= EF?????? ?B.?AB=2EF???????? ????C.?AB= EF?? ?????D.?AB= EF
9.如图,在菱形ABCD中,AC=6 ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( ??)
A.?6????????? ???? ?B.?3 ??????????????????? ???????C.?2 ??? ???????????D.?4.5
二、填空题
10.如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,A点的坐标是(0,4),则直线AC的表达式是________.
11.己知一个菱形的边长为2,较长的对角线长为2 ,则这个菱形的面积是________.
12.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0)点D在y轴上,则点C的坐标是________。
13.如图,已知菱形ABCD,对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是________.
14.如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为________.
15.如图,已知AB=8,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE的中点.当点P在线段AB上移动时,点M,N之间的距离最短为________(结果留根号).
16.如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小正三角形,若 = , 则正△ABC的边长是________.
三、解答题
17.如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点C作CE//AB,过点B作BE//CD,CE、BE相交于点E.求证:四边形BECD为菱形.
18.如图:在△ABC中,∠BAC = ,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
19.如图,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点F处,折痕交CD边于点E. 求证:四边形ADEF是菱形.
20.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN.求证:四边形ABCD是菱形.
21.如图,△ABC≌△ABD,点E在边AB上,并且CE∥BD,连接DE. 求证:四边形BCED是菱形.
22.如图,已知四边形ABCD是菱形,DE⊥AB,DF⊥BC,求证:△ADE≌△CDF. ?
23.如图,在?ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.
答案解析部分
一、单选题
1.【答案】C
【解析】A.改成为:对角线“互相平分”的四边形是平行四边形,故A不符合题意;B.改成为:对角线相等的“平行四边形”是矩形,故B不符合题意; C.正确,故C符合题意; D.改成为:对角线互相垂直且相等的“平行四边形”是正方形,故D不符合题意; 故答案为:C.
2.【答案】C
【解析】∵菱形ABCD的边长为2,∴AD=AB=2,又∵∠DAB=60°, ∴△DAB是等边三角形,∴AD=BD=AB=2,则对角线BD的长是2. 故答案为:C.
3.【答案】A
【解析】设对角线AC、BC交于点O,
∵四边形ABCD是菱形,AC=6,BD=8 ∴A0=3,BO=4,AC⊥BC,∴AB=5,∴C菱形ABCD=4×5=20. 故答案为:A.
4.【答案】A
【解析】∵菱形ABCD的周长为16,∴菱形ABCD的边长为4, ∵∠BAD=60°, ∴△ABD是等边三角形, 又∵O是菱形对角线AC、BD的交点, ∴AC⊥BD, 在Rt△AOD中, ∴AO= , ∴AC=2A0=4 , ∴S△ACD= ·OD·AC= ×2×4 =4 , 又∵O、E分别是中点, ∴OE∥AD, ∴△COE∽△CAD, ∴ , ∴ , ∴S△COE= S△CAD= ×4 = . 故答案为:A.
5.【答案】C
【解析】∵菱形ABCD的周长是16, ∴AB=AD=CD=BC=4, ∵∠A=60°, ∴△ABD是等边三角形, ∴AB=AD=BD=4. ∴对角线BD的长度为4. 故答案为:C.
6.【答案】A
【解析】∵E是AC中点, ∵EF∥BC,交AB于点F, ∴EF是△ABC的中位线, ∴BC=2EF=2×3=6, ∴菱形ABCD的周长是4×6=24, 故答案为:A.
7.【答案】B
【解析】∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,AB=BC=CD=AD, ∵AC=8cm,BD=6cm,∴AD=5cm,周长=4×5=20 cm, S菱形ABCD= AC?BD=24cm2 . 故答案为:B.
8.【答案】D
【解析】连接AC、BD交于点O, ∵四边形ABCD是菱形,∴OA= AC,OB= BD,AC⊥BD, ∵E、F、G、H分别是边AB、BC、CD和DA的中点, ∴EH= BD,EF= AC, ∵EH=2EF, ∴OA=EF,OB=2OA=2EF, 在Rt△AOB中,AB= = EF, 故答案为:D.
9.【答案】C
【解析】如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P, 则点P、M即为使PE+PM取得最小值的点, 则有PE+PM=PE′+PM=E′M, ∵四边形ABCD是菱形, ∴点E′在CD上, ∵AC=6 ,BD=6, ∴AB= , 由S菱形ABCD= AC?BD=AB?E′M得 ×6 ×6=3 ?E′M, 解得:E′M=2 , 即PE+PM的最小值是2 , 故答案为:C.
二、填空题
10.【答案】
【解析】如图, 由菱形OABC的一个顶点在原点O处,A点的坐标是(0,4),得OC=OA=4, 又∵∠1=60°, ∴∠2=30°, sin∠2= , ∴CD=2, cos∠2=cos30°= , OD=2 , ∴C(2 ,2), 设AC的解析式为y=kx+b, 将A,C点坐标代入函数解析式,得 , 解得 , 直线AC的表达式是y=﹣ x+4, 故答案为:y=﹣ x+4. 11.【答案】
【解析】依照题意画出图形,如图所示. 在Rt△AOB中,AB=2,OB= , ∴OA= =1, ∴AC=2OA=2, ∴S菱形ABCD= AC?BD= ×2×2 =2 . 故答案为:2 .
12.【答案】(-5,4)
【解析】∵A(3,0),B(-2,0), ∴AB=5,AO=3,BO=2, 又∵四边形ABCD为菱形, ∴AD=CD=BC=AB=5, 在Rt△AOD中, ∴OD=4, 作CE⊥x轴, ∴四边形OECD为矩形, ∴CE=OD=4,OE=CD=5, ∴C(-5,4). 故答案为:(-5,4).
13.【答案】2
【解析】∵四边形ABCD是菱形,AC=6,∴AC⊥BD,OA= AC=3,BD=2OB. 在Rt△OAB中,∵∠AOD=90°, ∴tan∠BAC= , ∴OB=1, ∴BD=2. 故答案为2.
14.【答案】2.8
【解析】作EH⊥BD于H, 由折叠的性质可知,EG=EA, 由题意得,BD=DG+BG=8, ∵四边形ABCD是菱形, ∴AD=AB,∠ABD=∠CBD= ∠ABC=60°, ∴△ABD为等边三角形, ∴AB=BD=8, 设BE=x,则EG=AE=8﹣x, 在Rt△EHB中,BH= x,EH= x, 在Rt△EHG中,EG2=EH2+GH2 , 即(8﹣x)2=( x)2+(6﹣x)2 , 解得,x=2.8,即BE=2.8, 故答案为:2.8.
15.【答案】2
【解析】连接PM、PN. ∵四边形APCD,四边形PBFE是菱形,∠DAP=60°, ∴∠APC=120°,∠EPB=60°, ∵M,N分别是对角线AC,BE的中点, ∴∠CPM= ∠APC=60°,∠EPN= ∠EPB=30°, ∴∠MPN=60°+30°=90°, 设PA=2a,则PB=8﹣2a,PM=a,PN= (4﹣a), ∴MN= = = , ∴a=3时,MN有最小值,最小值为2 , 故答案为2 .
16.【答案】12
【解析】设正△ABC的边长为x , 则高为 x , S△ABC= x· x= x2.∵所分成的都是正三角形,∴结合图形可得黑色菱形的较长的对角线为 x- , 较短的对角线为( x- ) = x-1, ∴黑色菱形的面积= (x-2)2 , ∴ = = , 整理得,11x2-144x+144=0,解得x1= (不符合题意,舍去),x2=12.∴△ABC的边长是12. 答案:12
三、解答题
17.【答案】证明:∵CE//AB,BE//CD, ∴四边形BECD是平行四边形. 又∵∠ACB=90°,CD为AB边上的中线, ∴CD= AB. 又∵CD为AB边上的中线 ∴BD= AB. ∴BD=CD. ∴平行四边形BECD是菱形
【解析】由平行四边形的定义可得四边形BECD是平行四边形,再证得一组邻边相等即可得解;由直角三角形斜边上的中线等于斜边的一半可得BD=CD,则根据有一组邻边相等的平行四边形是菱形可得平行四边形BECD是菱形。
18.【答案】证明:∵AD⊥BC, ∴∠ADB=90°, ∵∠BAC=90°, ∴∠B+∠BAD=90°,∠BAD+∠CAD=90°, ∴∠B=∠CAD, ∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA), ∴AE=EF(角平分线上的点到角两边的距离相等), ∵CE=CE,∴由勾股定理得:AC=CF, ∵△ACG和△FCG中 ? ∴△ACG≌△FCG, ∴∠CAD=∠CFG, ∵∠B=∠CAD ∴∠B=∠CFG, ∴GF∥AB, ∵AD⊥BC,EF⊥BC, ∴AD∥EF, 即AG∥EF,AE∥GF, ∴四边形AEFG是平行四边形, ∵AE=EF, ∴平行四边形AEFG是菱形.
【解析】由已知用边角边易证△ACG≌△FCG,可得∠CAD=∠CFG,结合已知条件易得∠B=∠CFG,由平行线的判定可得GF∥AB,根据同垂直于一条直线的两条直线互相平行可得AD∥EF,由两组对边分别平行的四边形是平行四边形可得四边形AEFG是平行四边形,再根据有一组邻边相等的平行四边形是菱形可得平行四边形AEFG是菱形.
19.【答案】证明:由折叠可知,DE=EF,AD=AF,∠DEA=∠FEA ∵四边形ABCD是平行四边形 ∴DE∥AF ∴∠DEA=∠EAF ∴∠EAF=∠FEA ∴AF=EF???? ∴AF=AD=DE=EF ∴四边形ADEF是菱形.
【解析】由折叠的性质和平行四边形的性质易证AF=AD=DE=EF,根据有四条边相等的四边形是菱形可得四边形ADEF是菱形。
20.【答案】证明:∵AD∥BC, ∴ , ? ∵∠BAD=∠BCD, ∴∠B=∠D, ∴四边形ABCD是平行四边形, ∵AM⊥BC,AN⊥DC, ∴ ? 在△ABM和△ADN中, ? ∴△ABM≌△ADN(AAS), ∴AB=AD, ∴四边形ABCD是菱形.
【解析】由题意易证两组对角相等的四边形是平行四边形可得四边形ABCD是平行四边形,结合已知用角角边易证△ABM≌△ADN,则可得AB=AD,由一组邻边相等的平行四边形是菱形可得四边形ABCD是菱形。
21.【答案】证明:∵ ≌ , ∴ ?, 在 和 中 , ∴ ≌ ?, ∴ , 又∵ , ∴ ?, ∴ , ∴ , ∴ , ∴四边形BCED是菱形.
【解析】由ΔABC≌ΔABD可得BC=BD,∠1=∠2 ,用边角边可证ΔBEC≌ΔBED,则CE=DE,根据平行线的性质易证CE=CB,于是有CE=CB=DB=DE,由四边都相等的四边形是菱形可得四边形BCED是菱形.
22.【答案】证明:∵四边形ABCD是菱形,∴∠A=∠C,AD=CD, 又∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°, 在△ADE和△CDF中, ,∴△ADE≌△CDF(AAS).
【解析】先利用菱形的性质可求出∠A=∠C,AD=CD,再结合已知条件DE⊥AB,DF⊥BC,可得∠AED=∠CFD,从而由AAS可证△ADE≌△CDF。
23.【答案】解:∵在?ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO, 在△EOD和△FOB中, , ∴△DOE≌△BOF(ASA),∴OE=OF,
又∵OB=OD,∴四边形EBFD是平行四边形, ∵EF⊥BD,∴四边形BFDE为菱形
【解析】根据平行四边形的性质,得出BO=DO,∠EDB=∠FBO,再利用ASA证明△DOE≌△BOF,得出OE=OF,就可证得四边形EBFD是平行四边形,然后根据对角线互相垂直的平行四边形是菱形,即可得证。
1.1 菱形的性质和判定练习题(含解析)
一、单选题
1.下列命题正确的是(?? )
A.对角线相等的四边形是平行四边形 B.对角线相等的四边形是矩形 C.对角线互相垂直的平行四边形是菱形 D.对角线互相垂直且相等的四边形是正方形
2.如图,已知菱形ABCD的边长等于2,若∠DAB=60°,则对角线BD的长为(?? )
A.?1??????????????????????????????????????B.???????????????????????????????????????C.?2?????????????????????????????????????D.?
3.如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是(??? )。
A.20 B.24 C.40 D.48
4.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是(?? )。
A.????????? ? ???B.?2????????? ???? ??????C.??????????????? ????????????D.?4
5.若菱形 的周长是16, ∠A=60° ,则对角线 的长度为( )
A.?2?????????????? ?????????B.?????? ??????????????????C.?4?????????????? ????????D.?
6.如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱
形ABCD的周长为(?? )
A.?24???????????????????? ?????????B.?18???????? ?????????????????C.?12??????????? ???????????D.?9
7.菱形 的两条对角线长分别为 和 ,则它的周长和面积分别为(? ? )
A.?? ???????????? ?????B.?? ???? ????C.?? ????????? ???????D.??
8.如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF,则下列结论正确的是( ??)
A.?AB= EF?????? ?B.?AB=2EF???????? ????C.?AB= EF?? ?????D.?AB= EF
9.如图,在菱形ABCD中,AC=6 ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( ??)
A.?6????????? ???? ?B.?3 ??????????????????? ???????C.?2 ??? ???????????D.?4.5
二、填空题
10.如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,A点的坐标是(0,4),则直线AC的表达式是________.
11.己知一个菱形的边长为2,较长的对角线长为2 ,则这个菱形的面积是________.
12.如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0)点D在y轴上,则点C的坐标是________。
13.如图,已知菱形ABCD,对角线AC,BD相交于点O.若tan∠BAC= ,AC=6,则BD的长是________.
14.如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为________.
15.如图,已知AB=8,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE的中点.当点P在线段AB上移动时,点M,N之间的距离最短为________(结果留根号).
16.如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小正三角形,若 = , 则正△ABC的边长是________.
三、解答题
17.如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点C作CE//AB,过点B作BE//CD,CE、BE相交于点E.求证:四边形BECD为菱形.
18.如图:在△ABC中,∠BAC = ,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
19.如图,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点F处,折痕交CD边于点E. 求证:四边形ADEF是菱形.
20.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN.求证:四边形ABCD是菱形.
21.如图,△ABC≌△ABD,点E在边AB上,并且CE∥BD,连接DE. 求证:四边形BCED是菱形.
22.如图,已知四边形ABCD是菱形,DE⊥AB,DF⊥BC,求证:△ADE≌△CDF. ?
23.如图,在?ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.
答案解析部分
一、单选题
1.【答案】C
【解析】A.改成为:对角线“互相平分”的四边形是平行四边形,故A不符合题意;B.改成为:对角线相等的“平行四边形”是矩形,故B不符合题意; C.正确,故C符合题意; D.改成为:对角线互相垂直且相等的“平行四边形”是正方形,故D不符合题意; 故答案为:C.
2.【答案】C
【解析】∵菱形ABCD的边长为2,∴AD=AB=2,又∵∠DAB=60°, ∴△DAB是等边三角形,∴AD=BD=AB=2,则对角线BD的长是2. 故答案为:C.
3.【答案】A
【解析】设对角线AC、BC交于点O,
∵四边形ABCD是菱形,AC=6,BD=8 ∴A0=3,BO=4,AC⊥BC,∴AB=5,∴C菱形ABCD=4×5=20. 故答案为:A.
4.【答案】A
【解析】∵菱形ABCD的周长为16,∴菱形ABCD的边长为4, ∵∠BAD=60°, ∴△ABD是等边三角形, 又∵O是菱形对角线AC、BD的交点, ∴AC⊥BD, 在Rt△AOD中, ∴AO= , ∴AC=2A0=4 , ∴S△ACD= ·OD·AC= ×2×4 =4 , 又∵O、E分别是中点, ∴OE∥AD, ∴△COE∽△CAD, ∴ , ∴ , ∴S△COE= S△CAD= ×4 = . 故答案为:A.
5.【答案】C
【解析】∵菱形ABCD的周长是16, ∴AB=AD=CD=BC=4, ∵∠A=60°, ∴△ABD是等边三角形, ∴AB=AD=BD=4. ∴对角线BD的长度为4. 故答案为:C.
6.【答案】A
【解析】∵E是AC中点, ∵EF∥BC,交AB于点F, ∴EF是△ABC的中位线, ∴BC=2EF=2×3=6, ∴菱形ABCD的周长是4×6=24, 故答案为:A.
7.【答案】B
【解析】∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,AB=BC=CD=AD, ∵AC=8cm,BD=6cm,∴AD=5cm,周长=4×5=20 cm, S菱形ABCD= AC?BD=24cm2 . 故答案为:B.
8.【答案】D
【解析】连接AC、BD交于点O, ∵四边形ABCD是菱形,∴OA= AC,OB= BD,AC⊥BD, ∵E、F、G、H分别是边AB、BC、CD和DA的中点, ∴EH= BD,EF= AC, ∵EH=2EF, ∴OA=EF,OB=2OA=2EF, 在Rt△AOB中,AB= = EF, 故答案为:D.
9.【答案】C
【解析】如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P, 则点P、M即为使PE+PM取得最小值的点, 则有PE+PM=PE′+PM=E′M, ∵四边形ABCD是菱形, ∴点E′在CD上, ∵AC=6 ,BD=6, ∴AB= , 由S菱形ABCD= AC?BD=AB?E′M得 ×6 ×6=3 ?E′M, 解得:E′M=2 , 即PE+PM的最小值是2 , 故答案为:C.
二、填空题
10.【答案】
【解析】如图, 由菱形OABC的一个顶点在原点O处,A点的坐标是(0,4),得OC=OA=4, 又∵∠1=60°, ∴∠2=30°, sin∠2= , ∴CD=2, cos∠2=cos30°= , OD=2 , ∴C(2 ,2), 设AC的解析式为y=kx+b, 将A,C点坐标代入函数解析式,得 , 解得 , 直线AC的表达式是y=﹣ x+4, 故答案为:y=﹣ x+4. 11.【答案】
【解析】依照题意画出图形,如图所示. 在Rt△AOB中,AB=2,OB= , ∴OA= =1, ∴AC=2OA=2, ∴S菱形ABCD= AC?BD= ×2×2 =2 . 故答案为:2 .
12.【答案】(-5,4)
【解析】∵A(3,0),B(-2,0), ∴AB=5,AO=3,BO=2, 又∵四边形ABCD为菱形, ∴AD=CD=BC=AB=5, 在Rt△AOD中, ∴OD=4, 作CE⊥x轴, ∴四边形OECD为矩形, ∴CE=OD=4,OE=CD=5, ∴C(-5,4). 故答案为:(-5,4).
13.【答案】2
【解析】∵四边形ABCD是菱形,AC=6,∴AC⊥BD,OA= AC=3,BD=2OB. 在Rt△OAB中,∵∠AOD=90°, ∴tan∠BAC= , ∴OB=1, ∴BD=2. 故答案为2.
14.【答案】2.8
【解析】作EH⊥BD于H, 由折叠的性质可知,EG=EA, 由题意得,BD=DG+BG=8, ∵四边形ABCD是菱形, ∴AD=AB,∠ABD=∠CBD= ∠ABC=60°, ∴△ABD为等边三角形, ∴AB=BD=8, 设BE=x,则EG=AE=8﹣x, 在Rt△EHB中,BH= x,EH= x, 在Rt△EHG中,EG2=EH2+GH2 , 即(8﹣x)2=( x)2+(6﹣x)2 , 解得,x=2.8,即BE=2.8, 故答案为:2.8.
15.【答案】2
【解析】连接PM、PN. ∵四边形APCD,四边形PBFE是菱形,∠DAP=60°, ∴∠APC=120°,∠EPB=60°, ∵M,N分别是对角线AC,BE的中点, ∴∠CPM= ∠APC=60°,∠EPN= ∠EPB=30°, ∴∠MPN=60°+30°=90°, 设PA=2a,则PB=8﹣2a,PM=a,PN= (4﹣a), ∴MN= = = , ∴a=3时,MN有最小值,最小值为2 , 故答案为2 .
16.【答案】12
【解析】设正△ABC的边长为x , 则高为 x , S△ABC= x· x= x2.∵所分成的都是正三角形,∴结合图形可得黑色菱形的较长的对角线为 x- , 较短的对角线为( x- ) = x-1, ∴黑色菱形的面积= (x-2)2 , ∴ = = , 整理得,11x2-144x+144=0,解得x1= (不符合题意,舍去),x2=12.∴△ABC的边长是12. 答案:12
三、解答题
17.【答案】证明:∵CE//AB,BE//CD, ∴四边形BECD是平行四边形. 又∵∠ACB=90°,CD为AB边上的中线, ∴CD= AB. 又∵CD为AB边上的中线 ∴BD= AB. ∴BD=CD. ∴平行四边形BECD是菱形
【解析】由平行四边形的定义可得四边形BECD是平行四边形,再证得一组邻边相等即可得解;由直角三角形斜边上的中线等于斜边的一半可得BD=CD,则根据有一组邻边相等的平行四边形是菱形可得平行四边形BECD是菱形。
18.【答案】证明:∵AD⊥BC, ∴∠ADB=90°, ∵∠BAC=90°, ∴∠B+∠BAD=90°,∠BAD+∠CAD=90°, ∴∠B=∠CAD, ∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA), ∴AE=EF(角平分线上的点到角两边的距离相等), ∵CE=CE,∴由勾股定理得:AC=CF, ∵△ACG和△FCG中 ? ∴△ACG≌△FCG, ∴∠CAD=∠CFG, ∵∠B=∠CAD ∴∠B=∠CFG, ∴GF∥AB, ∵AD⊥BC,EF⊥BC, ∴AD∥EF, 即AG∥EF,AE∥GF, ∴四边形AEFG是平行四边形, ∵AE=EF, ∴平行四边形AEFG是菱形.
【解析】由已知用边角边易证△ACG≌△FCG,可得∠CAD=∠CFG,结合已知条件易得∠B=∠CFG,由平行线的判定可得GF∥AB,根据同垂直于一条直线的两条直线互相平行可得AD∥EF,由两组对边分别平行的四边形是平行四边形可得四边形AEFG是平行四边形,再根据有一组邻边相等的平行四边形是菱形可得平行四边形AEFG是菱形.
19.【答案】证明:由折叠可知,DE=EF,AD=AF,∠DEA=∠FEA ∵四边形ABCD是平行四边形 ∴DE∥AF ∴∠DEA=∠EAF ∴∠EAF=∠FEA ∴AF=EF???? ∴AF=AD=DE=EF ∴四边形ADEF是菱形.
【解析】由折叠的性质和平行四边形的性质易证AF=AD=DE=EF,根据有四条边相等的四边形是菱形可得四边形ADEF是菱形。
20.【答案】证明:∵AD∥BC, ∴ , ? ∵∠BAD=∠BCD, ∴∠B=∠D, ∴四边形ABCD是平行四边形, ∵AM⊥BC,AN⊥DC, ∴ ? 在△ABM和△ADN中, ? ∴△ABM≌△ADN(AAS), ∴AB=AD, ∴四边形ABCD是菱形.
【解析】由题意易证两组对角相等的四边形是平行四边形可得四边形ABCD是平行四边形,结合已知用角角边易证△ABM≌△ADN,则可得AB=AD,由一组邻边相等的平行四边形是菱形可得四边形ABCD是菱形。
21.【答案】证明:∵ ≌ , ∴ ?, 在 和 中 , ∴ ≌ ?, ∴ , 又∵ , ∴ ?, ∴ , ∴ , ∴ , ∴四边形BCED是菱形.
【解析】由ΔABC≌ΔABD可得BC=BD,∠1=∠2 ,用边角边可证ΔBEC≌ΔBED,则CE=DE,根据平行线的性质易证CE=CB,于是有CE=CB=DB=DE,由四边都相等的四边形是菱形可得四边形BCED是菱形.
22.【答案】证明:∵四边形ABCD是菱形,∴∠A=∠C,AD=CD, 又∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°, 在△ADE和△CDF中, ,∴△ADE≌△CDF(AAS).
【解析】先利用菱形的性质可求出∠A=∠C,AD=CD,再结合已知条件DE⊥AB,DF⊥BC,可得∠AED=∠CFD,从而由AAS可证△ADE≌△CDF。
23.【答案】解:∵在?ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO, 在△EOD和△FOB中, , ∴△DOE≌△BOF(ASA),∴OE=OF,
又∵OB=OD,∴四边形EBFD是平行四边形, ∵EF⊥BD,∴四边形BFDE为菱形
【解析】根据平行四边形的性质,得出BO=DO,∠EDB=∠FBO,再利用ASA证明△DOE≌△BOF,得出OE=OF,就可证得四边形EBFD是平行四边形,然后根据对角线互相垂直的平行四边形是菱形,即可得证。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
