1.1.1 任意角29张PPT
图片预览






文档简介
课件29张PPT。1.1.1 任意角
温故而知新角的概念
初中是如何定义角的?
从一个点出发引出的
两条射线构成的几何图形.
初中学过的角的范围是:0o~ 360o.
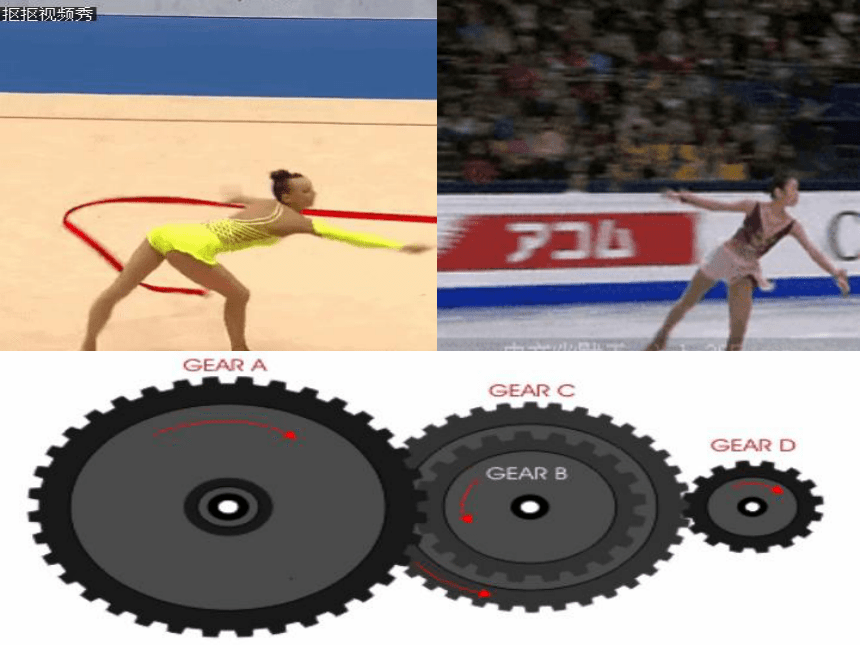
回归生活 你的手表慢了五分钟,
你是怎样将它校准的? 假如你的手表快了1.5小时,你应当如何将它校准?当时间校准后,分针旋转了多少度?1.既要知道旋转量; 2.又要知道旋转方向.因此,需要对角的概念进行推广.始边 终边顶点B新定义1. 角的概念的推广O 叫做角α的顶点,
OA叫做角α的始边,
OB叫做角α的终边.
.
“旋转”形成角
如图:一条射线的端点O,
它从起始位置OA按逆时针方向旋转到终止位置OB,形成了一个角α.用旋转来描述角,需要注意三个要素:
旋转中心、旋转方向和旋转量 (2)旋转方向:旋转变换的方向分为逆时针和顺时针两种,这是一对意义相反的量,根据以往的经验,我们可以把一对意义相反的量用正负数来表示.
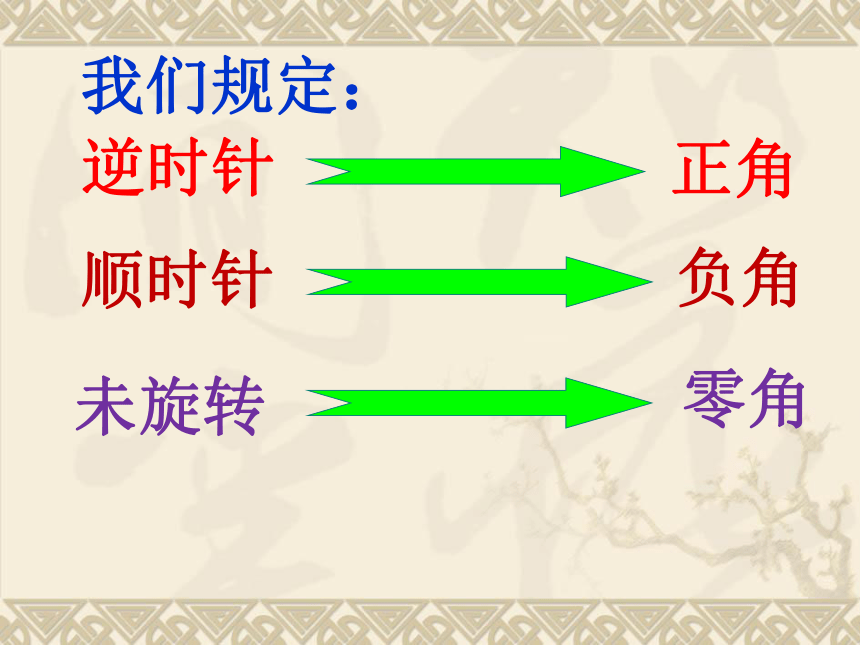
(1)旋转中心:作为角的顶点.逆时针正角顺时针负角未旋转零角我们规定:(3)旋转量:当旋转超过一周时,旋转量即超过360o,角度的绝对值可大于360o .于是就会出现720o , - 540o15′等角度.用“旋转”定义角之后,角的概念推广到了任意角如图:角的记法:在不引起混淆的前提下,“角α”或“∠α”可以简记成“α”.α=210°,β=-150°,γ =660°. 手表快了1.5小时,为了将它校准:方案一:将分针旋转 360?+180 ? = 540°方案二:将分针旋转
10*(-360?)+(-180 ?) = -3780°解决实际问题请大家画出60°的角动手画一画2.象限角
xoBy为了研究方便,我们往往在平面直角坐标系中来讨论角。角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合.那么,角的终边在第几象限,
我们就说这个角是第几象限的角。如果角的终边落在坐标轴上,
则该角不属于任何一个象限.在直角坐标系内讨论角有什么好处?2.角的终边绕原点旋转360?后回到原来的位置,很好地表现角的“周而复始”的变化规律.1.选取同一参照系,可以使角的讨论得到简化.想一想
? 60?
135 ?
300?
?330?
390?
xoy请回答以下的角是第几象限的角:是第四象限角,是第二象限角,是第一象限角,是第四象限角,是第一象限角. 将角按照上述方法放在直角坐标系中后,任意给定一个角,就有唯一的一条终边与之对应.反之,对于任意一条射线OB,以它为终边的角是否唯一确定?一起来探究那么终边相同的角有什么关系?不唯一xyoB30?一起来做游戏小球上记录了以下角度:30? 、210? 、390?、570? 、-150? 、-330?、-510? 、-690?,判断它们的终边是否与30?角的终边相同.3.终边相同的角 (1)观察:390?, -330?,-690?,它们的终边都与30?角的终边相同.(2)探究:
390?=30?+ , -330?=30 ?- ,
-690?=30?- , 30?=30 ?+ .
(3)结论:与30?终边相同的角可以表示为:
{β| β= 30? +k·360o, k∈Z} ,
即30?与整数个周角的和.S3={β| β= 30? +k·360o, k∈Z} S2={β| β= -330? +k·360o, k∈Z} S1={β| β= 390? +k·360o, k∈Z} 比较一下S1= S2= S3所有与?终边相同的角,连同?在内,可以构成一个集合:推广至一般性结论:即任何一个与角?终边相同的角,都可以表示成角?与整数个周角的和.S={β| β=α+k·360o, k∈Z}对于S={β| β=α+k·360o, k∈Z}
注意以下几点:
① k∈Z,
k > 0,表示在α的基础上逆时针旋转,
k < 0 ,表示在α的基础上顺时针旋转,
k = 0 ,即为α.
② ?不唯一;
③ 终边相同的角不一定相等,终边相同的角有无限多个,它们相差360o的整数倍.注意! -1050o是否与
30? 的终边相同.
思考一下已知:与30?终边相同的角可以表示为{β| β= 30? +k·360o, k∈Z} 例1. 在0o~360o范围内,找出与-950o12′终边相同的角,并判断它是哪个象限的角.
解:-950o12′=129o48′-3×360?
所以在0o~360o范围内,与-950o12′终边相同的角是129o48′,它是第二象限的角.
xoB30?-150? yC再想想终边在坐标轴上的角的表示 {β| β=90o+k·360o, k∈Z}{β| β=90o+k·180o, k∈Z}{β| β=k·90o, k∈Z}例2. 写出终边在直线y=x上的角的集合S,并把S中在-360o~720o间的角写出来.满足要求的元素是
45?-2×180?= -315?,45?-1×180?= -135?,
45?+0×180?= 45?, 45?+1×180?= 225?,
45?+2×180?= 405?, 45?+3×180?= 585?.
解:集合S={β| β=45o+k·180o, k∈Z}正角
负角
零角象限角
终边相同的角的表示任意角P5 练习
3.4.5作业: 谢谢大家!
温故而知新角的概念
初中是如何定义角的?
从一个点出发引出的
两条射线构成的几何图形.
初中学过的角的范围是:0o~ 360o.
回归生活 你的手表慢了五分钟,
你是怎样将它校准的? 假如你的手表快了1.5小时,你应当如何将它校准?当时间校准后,分针旋转了多少度?1.既要知道旋转量; 2.又要知道旋转方向.因此,需要对角的概念进行推广.始边 终边顶点B新定义1. 角的概念的推广O 叫做角α的顶点,
OA叫做角α的始边,
OB叫做角α的终边.
.
“旋转”形成角
如图:一条射线的端点O,
它从起始位置OA按逆时针方向旋转到终止位置OB,形成了一个角α.用旋转来描述角,需要注意三个要素:
旋转中心、旋转方向和旋转量 (2)旋转方向:旋转变换的方向分为逆时针和顺时针两种,这是一对意义相反的量,根据以往的经验,我们可以把一对意义相反的量用正负数来表示.
(1)旋转中心:作为角的顶点.逆时针正角顺时针负角未旋转零角我们规定:(3)旋转量:当旋转超过一周时,旋转量即超过360o,角度的绝对值可大于360o .于是就会出现720o , - 540o15′等角度.用“旋转”定义角之后,角的概念推广到了任意角如图:角的记法:在不引起混淆的前提下,“角α”或“∠α”可以简记成“α”.α=210°,β=-150°,γ =660°. 手表快了1.5小时,为了将它校准:方案一:将分针旋转 360?+180 ? = 540°方案二:将分针旋转
10*(-360?)+(-180 ?) = -3780°解决实际问题请大家画出60°的角动手画一画2.象限角
xoBy为了研究方便,我们往往在平面直角坐标系中来讨论角。角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合.那么,角的终边在第几象限,
我们就说这个角是第几象限的角。如果角的终边落在坐标轴上,
则该角不属于任何一个象限.在直角坐标系内讨论角有什么好处?2.角的终边绕原点旋转360?后回到原来的位置,很好地表现角的“周而复始”的变化规律.1.选取同一参照系,可以使角的讨论得到简化.想一想
? 60?
135 ?
300?
?330?
390?
xoy请回答以下的角是第几象限的角:是第四象限角,是第二象限角,是第一象限角,是第四象限角,是第一象限角. 将角按照上述方法放在直角坐标系中后,任意给定一个角,就有唯一的一条终边与之对应.反之,对于任意一条射线OB,以它为终边的角是否唯一确定?一起来探究那么终边相同的角有什么关系?不唯一xyoB30?一起来做游戏小球上记录了以下角度:30? 、210? 、390?、570? 、-150? 、-330?、-510? 、-690?,判断它们的终边是否与30?角的终边相同.3.终边相同的角 (1)观察:390?, -330?,-690?,它们的终边都与30?角的终边相同.(2)探究:
390?=30?+ , -330?=30 ?- ,
-690?=30?- , 30?=30 ?+ .
(3)结论:与30?终边相同的角可以表示为:
{β| β= 30? +k·360o, k∈Z} ,
即30?与整数个周角的和.S3={β| β= 30? +k·360o, k∈Z} S2={β| β= -330? +k·360o, k∈Z} S1={β| β= 390? +k·360o, k∈Z} 比较一下S1= S2= S3所有与?终边相同的角,连同?在内,可以构成一个集合:推广至一般性结论:即任何一个与角?终边相同的角,都可以表示成角?与整数个周角的和.S={β| β=α+k·360o, k∈Z}对于S={β| β=α+k·360o, k∈Z}
注意以下几点:
① k∈Z,
k > 0,表示在α的基础上逆时针旋转,
k < 0 ,表示在α的基础上顺时针旋转,
k = 0 ,即为α.
② ?不唯一;
③ 终边相同的角不一定相等,终边相同的角有无限多个,它们相差360o的整数倍.注意! -1050o是否与
30? 的终边相同.
思考一下已知:与30?终边相同的角可以表示为{β| β= 30? +k·360o, k∈Z} 例1. 在0o~360o范围内,找出与-950o12′终边相同的角,并判断它是哪个象限的角.
解:-950o12′=129o48′-3×360?
所以在0o~360o范围内,与-950o12′终边相同的角是129o48′,它是第二象限的角.
xoB30?-150? yC再想想终边在坐标轴上的角的表示 {β| β=90o+k·360o, k∈Z}{β| β=90o+k·180o, k∈Z}{β| β=k·90o, k∈Z}例2. 写出终边在直线y=x上的角的集合S,并把S中在-360o~720o间的角写出来.满足要求的元素是
45?-2×180?= -315?,45?-1×180?= -135?,
45?+0×180?= 45?, 45?+1×180?= 225?,
45?+2×180?= 405?, 45?+3×180?= 585?.
解:集合S={β| β=45o+k·180o, k∈Z}正角
负角
零角象限角
终边相同的角的表示任意角P5 练习
3.4.5作业: 谢谢大家!
