3.3.2 简单的线性规划问题34张PPT
文档属性
| 名称 | 3.3.2 简单的线性规划问题34张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 684.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-31 00:00:00 | ||
图片预览







文档简介
课件34张PPT。简单线性规划(二) 问题情景: 同学们闭上眼睛憧憬一下未来,假如十年后你是公司的生产设计工程师,坐在宽敞的办公室里,思考着如何安排公司的生产,你会考虑什么问题呢?问题探究: 若你负责下的某车间能生产甲、乙两种产品,每天生产甲产品x吨,乙产品y吨,由于生产设备和人员的限制 ,每天生产两种产品的总量不小于1吨,不大于3 吨,两种产品的相差值不超过1吨. 问:根据题意写出x、y满足的不等式组? 探究一:若生产1吨甲产品可获利2万元,生产1吨乙产品可获利1万元,则该车间每天最高可获利多少万元? 即令z=2x+y,则z的最大值是多少?探究一:
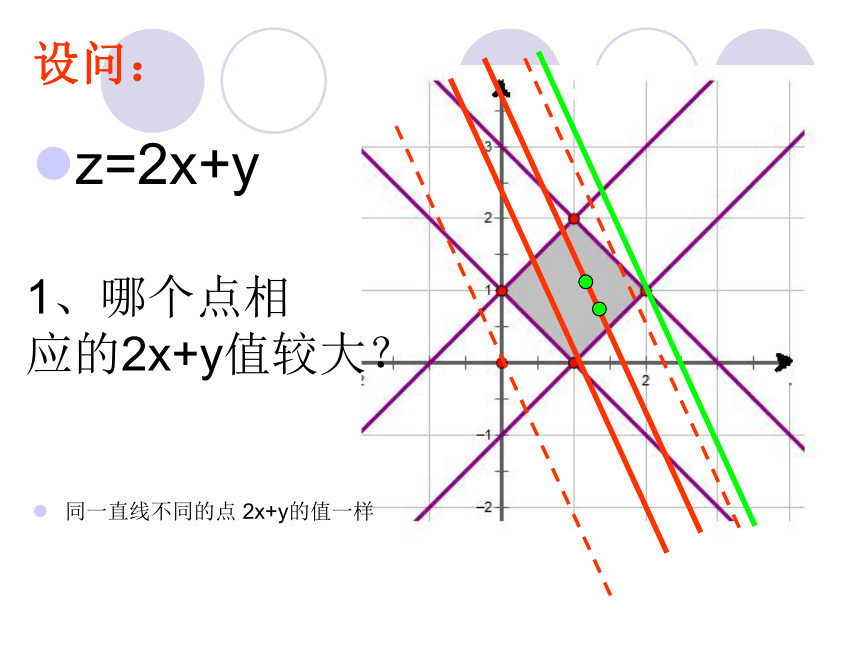
z=2x+y,则z的最大值是多少?
z=2x+y1、哪个点相 应的2x+y值较大?设问:
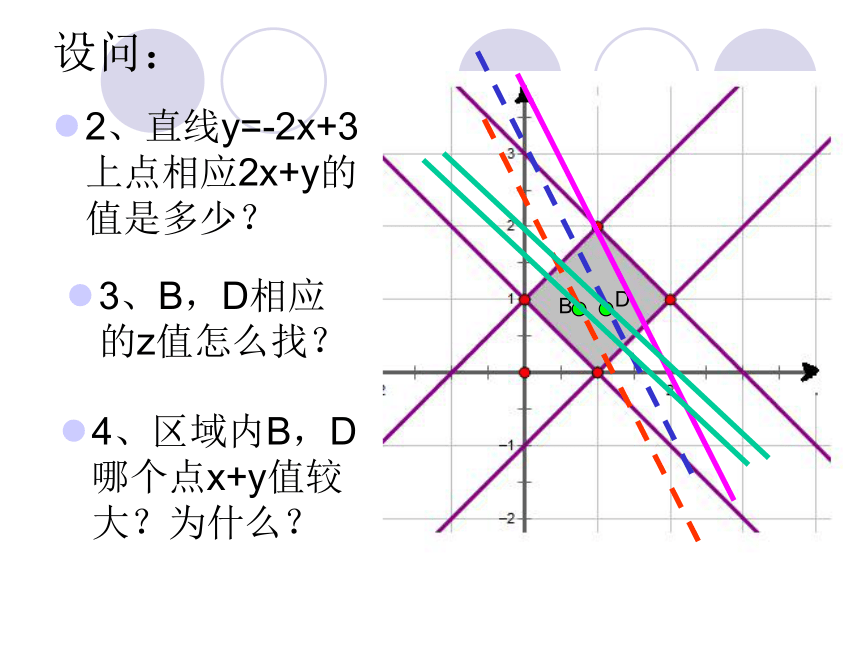
同一直线不同的点 2x+y的值一样设问: 3、B,D相应的z值怎么找?4、区域内B,D 哪个点x+y值较大?为什么?BD2、直线y=-2x+3上点相应2x+y的值是多少? 解题反思
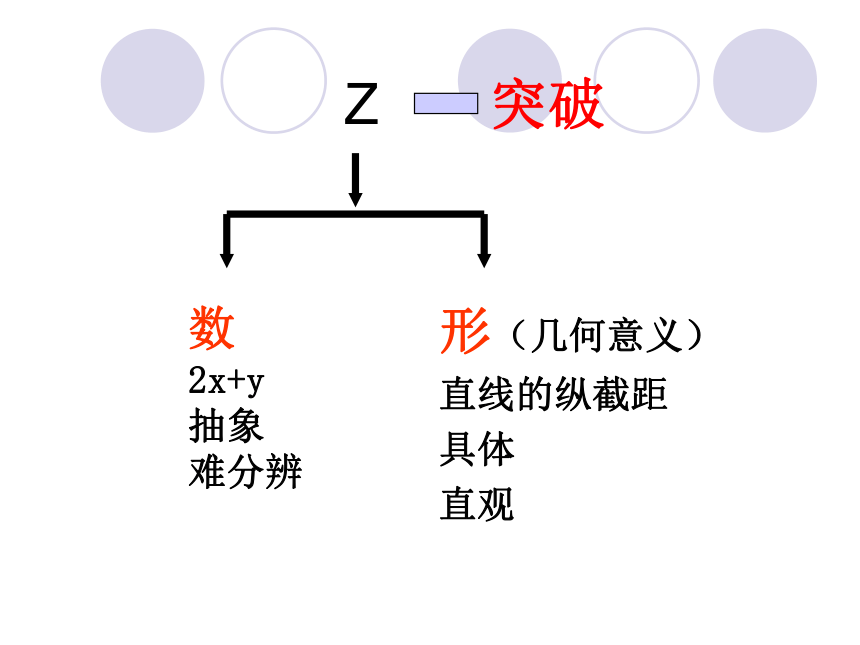
形(几何意义)
直线的纵截距
具体
直观 数
2x+y
抽象
难分辨Z 突破
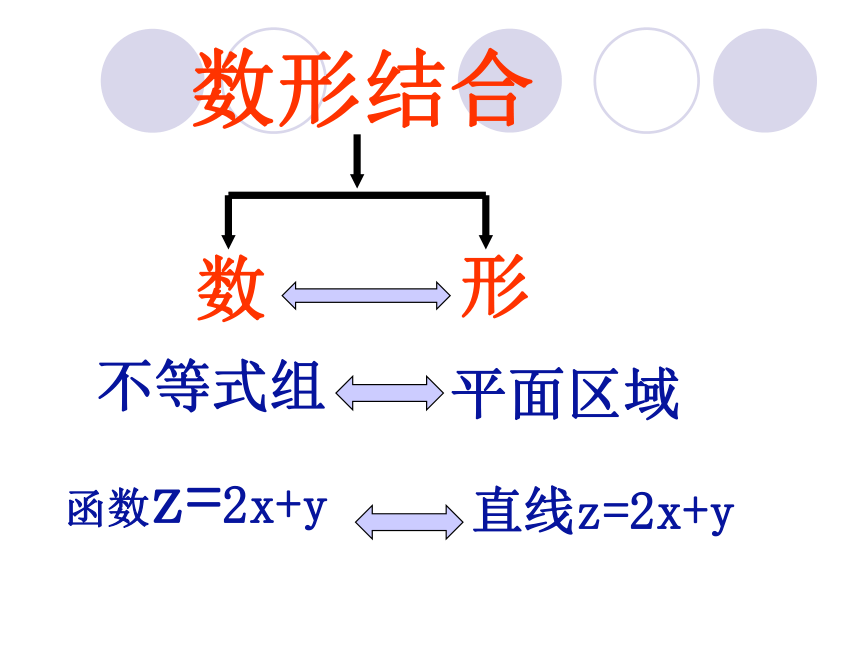
形 数数形结合
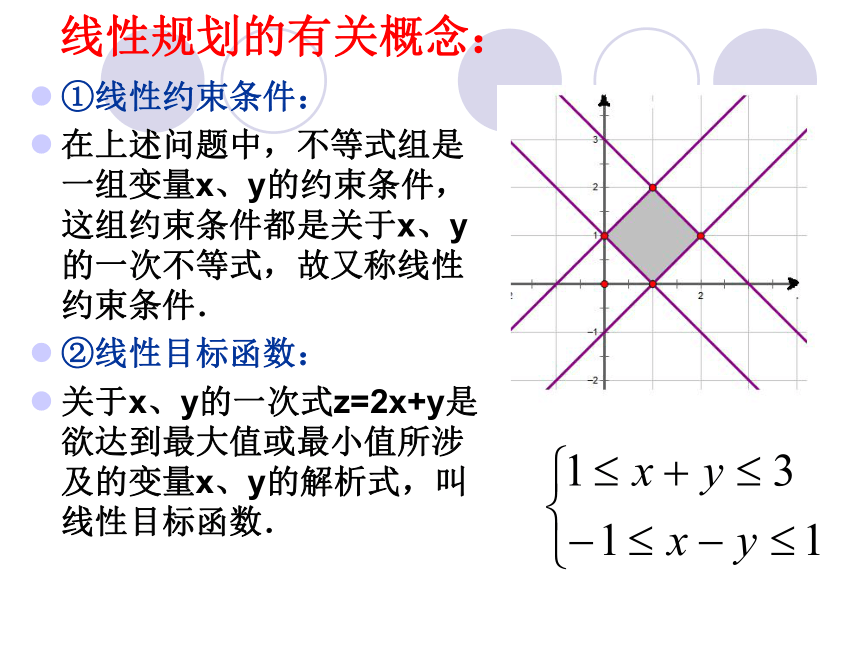
不等式组 平面区域 函数z=2x+y 直线z=2x+y线性规划的有关概念: ①线性约束条件:
在上述问题中,不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.
②线性目标函数:
关于x、y的一次式z=2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式,叫线性目标函数.线性规划的有关概念:
③可行解、可行域和最优解:
满足线性约束条件的解(x,y)叫可行解.
由所有可行解组成的集合叫做可行域.
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.
④线性规划问题:
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.探究猜想: (特殊---一般)(一般---特殊)探究二:变1:求z=x-2y,z的最大值和最优解?探究二:变1:求z=x-2y,z的最大值和最优解?设问:
1、该点相应的x-2y等于多少?2、怎么求z的值? 解题反思数形形数反思2:还有什么启发?z是一个与截距有关系的量,但未必就是截距,解题中先找z的几何意义。
解题反思探究三:自由探究探究三:探究三:设问:
2、对本题来说斜率在什么范围分别在A、B、C处取最优解?1、为什么最优点在A处,而不在C处?是什么量决定的?设问:3、斜率为多少最优解有无数个?斜率为多少最优解有无数个?设问:变1:p(x,y)在如图区域内,若z=x-ay且 z在C处取最小值求a的取值范围.探究三:问题延伸……线性规划,联想也可以用来解决x、y的一些非线性问题,比如xy、y/x呢?等我们学习更多的知识就可解决。
线性规划被誉为20世纪对科学发展和工程实践影响最大的十大算法之一,在很多实际问题中都有非常重要的应用,下节课我们研究它的实际应用。 课堂小结我学习了……
我感受到了……
我将继续学习的……
hua画化华画画图化实际问题 数学问题不等式组 平面区域抽象 具体函数Z=2x+y 方程Z=2x+y
方程Z=2x+y 直线Z=2x+y
变:直线Z=2x+y点 不变:相应2x+y值特殊 一般
华升华谢谢!
z=2x+y,则z的最大值是多少?
z=2x+y1、哪个点相 应的2x+y值较大?设问:
同一直线不同的点 2x+y的值一样设问: 3、B,D相应的z值怎么找?4、区域内B,D 哪个点x+y值较大?为什么?BD2、直线y=-2x+3上点相应2x+y的值是多少? 解题反思
形(几何意义)
直线的纵截距
具体
直观 数
2x+y
抽象
难分辨Z 突破
形 数数形结合
不等式组 平面区域 函数z=2x+y 直线z=2x+y线性规划的有关概念: ①线性约束条件:
在上述问题中,不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.
②线性目标函数:
关于x、y的一次式z=2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式,叫线性目标函数.线性规划的有关概念:
③可行解、可行域和最优解:
满足线性约束条件的解(x,y)叫可行解.
由所有可行解组成的集合叫做可行域.
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.
④线性规划问题:
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.探究猜想: (特殊---一般)(一般---特殊)探究二:变1:求z=x-2y,z的最大值和最优解?探究二:变1:求z=x-2y,z的最大值和最优解?设问:
1、该点相应的x-2y等于多少?2、怎么求z的值? 解题反思数形形数反思2:还有什么启发?z是一个与截距有关系的量,但未必就是截距,解题中先找z的几何意义。
解题反思探究三:自由探究探究三:探究三:设问:
2、对本题来说斜率在什么范围分别在A、B、C处取最优解?1、为什么最优点在A处,而不在C处?是什么量决定的?设问:3、斜率为多少最优解有无数个?斜率为多少最优解有无数个?设问:变1:p(x,y)在如图区域内,若z=x-ay且 z在C处取最小值求a的取值范围.探究三:问题延伸……线性规划,联想也可以用来解决x、y的一些非线性问题,比如xy、y/x呢?等我们学习更多的知识就可解决。
线性规划被誉为20世纪对科学发展和工程实践影响最大的十大算法之一,在很多实际问题中都有非常重要的应用,下节课我们研究它的实际应用。 课堂小结我学习了……
我感受到了……
我将继续学习的……
hua画化华画画图化实际问题 数学问题不等式组 平面区域抽象 具体函数Z=2x+y 方程Z=2x+y
方程Z=2x+y 直线Z=2x+y
变:直线Z=2x+y点 不变:相应2x+y值特殊 一般
华升华谢谢!
