探究与发现 解三角形的进一步讨论25张PPT
文档属性
| 名称 | 探究与发现 解三角形的进一步讨论25张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 471.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-08-31 00:00:00 | ||
图片预览








文档简介
课件25张PPT。正弦定理与余弦定理1解三角的进一步讨论正弦定理与余弦定理11、三角形中的边角关系(1)角与角之间的关系: (2)边与角之间的关系:? 正弦定理:余弦定理:射影定理:正弦定理与余弦定理12、正弦定理的另三种表示形式:正弦定理与余弦定理13、余弦定理的另一种表示形式 zxxk
正弦定理与余弦定理14、正弦定理解三角形可解决的类型:
(1)已知两角和任一边解三角形;
(2)已知两边和一边的对角解三角形.5、余弦定理解三角形可解决的类型:
(1)已知三边解三角形;
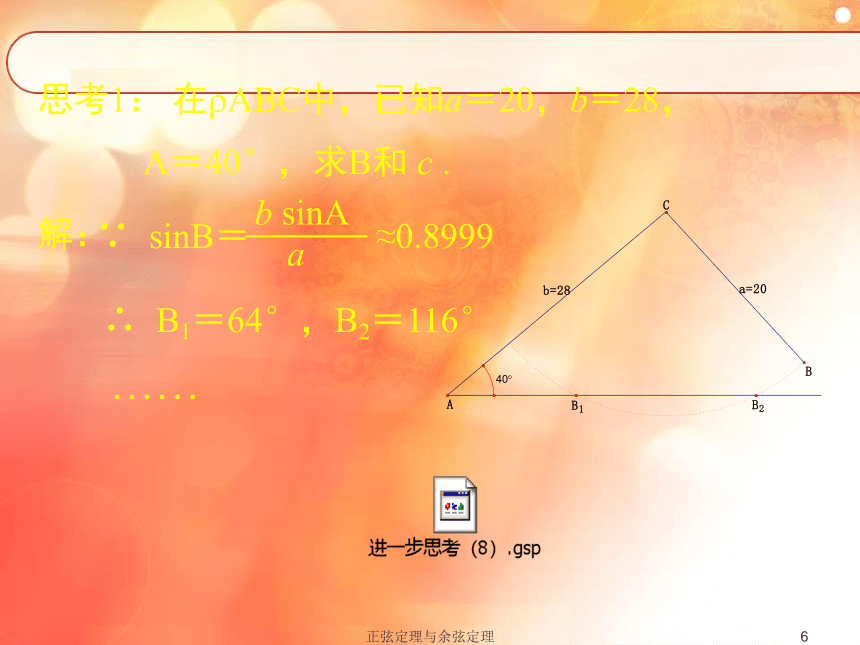
(2)已知两边和夹角解三角形.正弦定理与余弦定理1思考1: 在?ABC中,已知a=20,b=28,
A=40°,求B和 c .解:∴ B1=64°,B2=116°······正弦定理与余弦定理1 在上例 中,将已知条件改为以下几种情况,结果如何?(2) b=20,A=60°,a=10 ;(3) b=20,A=60°,a=15.(1) b=20,A=60°,a=20 ;正弦定理与余弦定理1(1) b=20,A=60°,a=20∵ 150°+60°> 180°,∴ B=150°应舍去.正弦定理与余弦定理1(2) b=20,A=60°,a=10B=90°.正弦定理与余弦定理1(3) ∴ 无解. 思考:已知两边和其中一边所对的角,
讨论 解三角形的解的情况?正弦定理与余弦定理1二、难点剖析 1、已知两边和其中一边的对角,解三角形时,将出现无解、一解和两解的情况,应分情况予以讨论.
下图即是表示在△ABC中,已知a、b和A时解三角形的各种情况.Z.xxk
正弦定理与余弦定理1(1)当A为锐角时(如下图)正弦定理与余弦定理1(2)当A为直角或钝角时(如下图),正弦定理与余弦定理1随堂练习1:不解三角形,判断三角形的个数.(1)a=5,b=4,A=120°
(2)a=30,b=30,A=50°
(3)a=7,b=14,A=30°
(4)a=9,b=10,A=60°
(5)a=6,b=9,A=45°
(6)c=50,b=72,C=135°正弦定理与余弦定理1解析正弦定理与余弦定理1思考2:能否用余弦定理求解两边及夹角?利用方程的思想和余弦定理:等式便成为方程.式中有四个量,知道任意三个,便正弦定理与余弦定理1 已知两边和其中一边的对角的解三角形问题,可运用正弦定理来求解,但应注意解的情况,或借助余弦定理,先求出c后,再求出角A与角C.分析正弦定理与余弦定理1正弦定理与余弦定理1正弦定理与余弦定理1分析 由已知设AB=7x,AC=8x,故要求AD的长只要求出x,△ABC中已知三边只需再有一个角,根据余弦定理便可求x,而用正弦定理正好可求角C.正弦定理与余弦定理1 解:在△ABC中,设AB=7x,AC=8x.
由正弦定理得 再由余弦定理得
(7x)2=(8x)2+152-2·8x·15cos60°,
∴x2-8x+15=0,∴x=3或x=5,
∴AB=21或AB=35.正弦定理与余弦定理1思考3:利用余弦定理可以判断三角形形状:练习、在△ABC中,已知a=7,b=10, c=5,判断△ABC 的形状。 正弦定理与余弦定理1随堂练习:一钝角三角形的边长为连续自然数,则这三边长为( )
A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,6分析: 要看哪一组符合要求,只需检验哪一个选项
中的最大角是钝角,即该角的余弦值小于0。B中: ,所以C是钝角D中: ,所以C是锐角,
因此以4,5,6为三边长的三角形是锐角三角形A、C显然不满足B正弦定理与余弦定理1小结:(1)已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形 (2)利用方程的思想和余弦定理,余弦公式中有四个量,知道任意三个,便可以解出另一个,运用此式可以求a或b或c或cosA(3)由余弦定理判断三角形的形状,求三角形的面积正弦定理与余弦定理1谢谢!
正弦定理与余弦定理14、正弦定理解三角形可解决的类型:
(1)已知两角和任一边解三角形;
(2)已知两边和一边的对角解三角形.5、余弦定理解三角形可解决的类型:
(1)已知三边解三角形;
(2)已知两边和夹角解三角形.正弦定理与余弦定理1思考1: 在?ABC中,已知a=20,b=28,
A=40°,求B和 c .解:∴ B1=64°,B2=116°······正弦定理与余弦定理1 在上例 中,将已知条件改为以下几种情况,结果如何?(2) b=20,A=60°,a=10 ;(3) b=20,A=60°,a=15.(1) b=20,A=60°,a=20 ;正弦定理与余弦定理1(1) b=20,A=60°,a=20∵ 150°+60°> 180°,∴ B=150°应舍去.正弦定理与余弦定理1(2) b=20,A=60°,a=10B=90°.正弦定理与余弦定理1(3) ∴ 无解. 思考:已知两边和其中一边所对的角,
讨论 解三角形的解的情况?正弦定理与余弦定理1二、难点剖析 1、已知两边和其中一边的对角,解三角形时,将出现无解、一解和两解的情况,应分情况予以讨论.
下图即是表示在△ABC中,已知a、b和A时解三角形的各种情况.Z.xxk
正弦定理与余弦定理1(1)当A为锐角时(如下图)正弦定理与余弦定理1(2)当A为直角或钝角时(如下图),正弦定理与余弦定理1随堂练习1:不解三角形,判断三角形的个数.(1)a=5,b=4,A=120°
(2)a=30,b=30,A=50°
(3)a=7,b=14,A=30°
(4)a=9,b=10,A=60°
(5)a=6,b=9,A=45°
(6)c=50,b=72,C=135°正弦定理与余弦定理1解析正弦定理与余弦定理1思考2:能否用余弦定理求解两边及夹角?利用方程的思想和余弦定理:等式便成为方程.式中有四个量,知道任意三个,便正弦定理与余弦定理1 已知两边和其中一边的对角的解三角形问题,可运用正弦定理来求解,但应注意解的情况,或借助余弦定理,先求出c后,再求出角A与角C.分析正弦定理与余弦定理1正弦定理与余弦定理1正弦定理与余弦定理1分析 由已知设AB=7x,AC=8x,故要求AD的长只要求出x,△ABC中已知三边只需再有一个角,根据余弦定理便可求x,而用正弦定理正好可求角C.正弦定理与余弦定理1 解:在△ABC中,设AB=7x,AC=8x.
由正弦定理得 再由余弦定理得
(7x)2=(8x)2+152-2·8x·15cos60°,
∴x2-8x+15=0,∴x=3或x=5,
∴AB=21或AB=35.正弦定理与余弦定理1思考3:利用余弦定理可以判断三角形形状:练习、在△ABC中,已知a=7,b=10, c=5,判断△ABC 的形状。 正弦定理与余弦定理1随堂练习:一钝角三角形的边长为连续自然数,则这三边长为( )
A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,6分析: 要看哪一组符合要求,只需检验哪一个选项
中的最大角是钝角,即该角的余弦值小于0。B中: ,所以C是钝角D中: ,所以C是锐角,
因此以4,5,6为三边长的三角形是锐角三角形A、C显然不满足B正弦定理与余弦定理1小结:(1)已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形 (2)利用方程的思想和余弦定理,余弦公式中有四个量,知道任意三个,便可以解出另一个,运用此式可以求a或b或c或cosA(3)由余弦定理判断三角形的形状,求三角形的面积正弦定理与余弦定理1谢谢!
