2.3.1 变量间的相关关系 课件1
文档属性
| 名称 | 2.3.1 变量间的相关关系 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-01 00:00:00 | ||
图片预览







文档简介
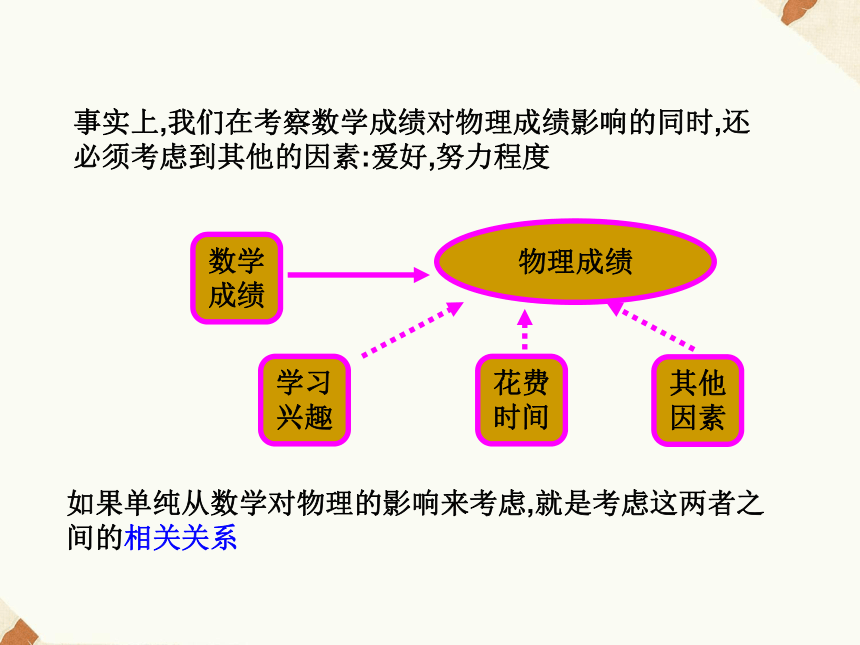
课件27张PPT。2.3.1 变量间的相关关系第二章 统 计小明,你数学成绩不太好,物理怎么样?也不太好啊.学不好数学,物理也是学不好的?????...事实上,我们在考察数学成绩对物理成绩影响的同时,还必须考虑到其他的因素:爱好,努力程度如果单纯从数学对物理的影响来考虑,就是考虑这两者之间的相关关系物理成绩数学成绩学习兴趣花费时间其他因素变量间的相关关系在我们的生活中广泛存在:
如: (1)商品销售收入与广告支出经费之间的关系
(2)粮食产量与施肥量之间的关系
(3)人体内脂肪含量与年龄之间的关系1.问题导航
(1)相关关系分为哪两种?
(2)什么叫散点图?
(3)什么叫回归直线?求回归直线的方法及步骤是什么?
2.例题导读
通过对例题的学习,(1)学会如何作散点图;(2)学会如何用散点图判断两个变量是否相关;(3)掌握求回归直线方程的方法;(4)熟悉回归直线方程的实际应用. ②.两个变量之间产生相关关系的原因是受许多不确定的随机因素的影响.注①.变量之间除了函数关系外,还有相关关系.1.相关关系:
⑴.两个变量之间的关系:
①.确定的关系:当自变量取值一定时,因变量也确定(如:函数关系)
②.非确定性关系:当自变量取值一定时,因变量带有随机性.相关关系是一种非确定性关系.
②.正相关与负相关
ⅰ.正相关:散点图中的点从左下到右上分布.
ⅱ.负相关:散点图中的点从左上到右下分布.①.散点图:将样本中n个数据点(xi,yi)(i=1,2,
…,n)描在平面直角坐标系中得到的图形.③线性相关关系:所有的样本点在某一直线附近
非线性相关关系:样本点都落在某一曲线附近⑵.相关关系分类
一条直线回归直线距离的平方和线性相关斜 率截 距2√√√×解析:A、B为函数关系,D无相关关系.C解析:①正方形的边长与面积之间的关系是函数关系.②水稻产量与施肥量之间的关系不是严格的函数关系,但是具有相关性,因而是相关关系.③人的身高与年龄之间的关系既不是函数关系,也不是相关关系,因为人的年龄达到一定时期身高就不发生明显变化了,因而它们不具备相关关系.②相关关系的判断③(2)下表是某地的年降雨量与年平均气温,判断两者是相关关系吗?求回归直线方程有意义吗?解:以x轴为年平均气温,y轴为年降雨量,可得相应的散点图,如图所示:因为图中各点并不在一条直线附近,
所以两者不具有相关关系,求回归
直线方程也是没有意义的.CA.变量x与y正相关,u与v正相关 B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关 D.变量x与y负相关,u与v负相关(2)下面是随机抽取的9名15岁男生的身高、体重表:判断所给的两个变量是否存在相关关系.解:以x轴表示身高,以y轴表示体重,得散点图:随着身高的增高,体重基本上
呈增加趋势.所以体重与身高
之间存在相关关系,并且是正
相关.线性回归方程的建立[解] (1)散点图如图:(3)当x=100时,y=0.7×100+0.35=70.35(吨标准煤),
90-70.35=19.65(吨标准煤).由此可预测生产100吨甲产品的生产能耗比技改前大约降低了19.65吨标准煤.2练习:
如: (1)商品销售收入与广告支出经费之间的关系
(2)粮食产量与施肥量之间的关系
(3)人体内脂肪含量与年龄之间的关系1.问题导航
(1)相关关系分为哪两种?
(2)什么叫散点图?
(3)什么叫回归直线?求回归直线的方法及步骤是什么?
2.例题导读
通过对例题的学习,(1)学会如何作散点图;(2)学会如何用散点图判断两个变量是否相关;(3)掌握求回归直线方程的方法;(4)熟悉回归直线方程的实际应用. ②.两个变量之间产生相关关系的原因是受许多不确定的随机因素的影响.注①.变量之间除了函数关系外,还有相关关系.1.相关关系:
⑴.两个变量之间的关系:
①.确定的关系:当自变量取值一定时,因变量也确定(如:函数关系)
②.非确定性关系:当自变量取值一定时,因变量带有随机性.相关关系是一种非确定性关系.
②.正相关与负相关
ⅰ.正相关:散点图中的点从左下到右上分布.
ⅱ.负相关:散点图中的点从左上到右下分布.①.散点图:将样本中n个数据点(xi,yi)(i=1,2,
…,n)描在平面直角坐标系中得到的图形.③线性相关关系:所有的样本点在某一直线附近
非线性相关关系:样本点都落在某一曲线附近⑵.相关关系分类
一条直线回归直线距离的平方和线性相关斜 率截 距2√√√×解析:A、B为函数关系,D无相关关系.C解析:①正方形的边长与面积之间的关系是函数关系.②水稻产量与施肥量之间的关系不是严格的函数关系,但是具有相关性,因而是相关关系.③人的身高与年龄之间的关系既不是函数关系,也不是相关关系,因为人的年龄达到一定时期身高就不发生明显变化了,因而它们不具备相关关系.②相关关系的判断③(2)下表是某地的年降雨量与年平均气温,判断两者是相关关系吗?求回归直线方程有意义吗?解:以x轴为年平均气温,y轴为年降雨量,可得相应的散点图,如图所示:因为图中各点并不在一条直线附近,
所以两者不具有相关关系,求回归
直线方程也是没有意义的.CA.变量x与y正相关,u与v正相关 B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关 D.变量x与y负相关,u与v负相关(2)下面是随机抽取的9名15岁男生的身高、体重表:判断所给的两个变量是否存在相关关系.解:以x轴表示身高,以y轴表示体重,得散点图:随着身高的增高,体重基本上
呈增加趋势.所以体重与身高
之间存在相关关系,并且是正
相关.线性回归方程的建立[解] (1)散点图如图:(3)当x=100时,y=0.7×100+0.35=70.35(吨标准煤),
90-70.35=19.65(吨标准煤).由此可预测生产100吨甲产品的生产能耗比技改前大约降低了19.65吨标准煤.2练习:
