2018_2019高中物理第3章力与相互作用3.2弹力学案沪科版必修1
文档属性
| 名称 | 2018_2019高中物理第3章力与相互作用3.2弹力学案沪科版必修1 |

|
|
| 格式 | zip | ||
| 文件大小 | 973.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-09-01 00:00:00 | ||
图片预览




文档简介
3.2 弹力
[目标定位] 1.知道形变的概念,并会区分某种形变是弹性形变还是非弹性形变.2.知道弹力的定义及产生的条件,会判断两个物体间是否存在弹力,并会判断弹力的方向.3.掌握胡克定律并能用此定律解决有关问题.
一、形变和弹力
[问题设计]
(1)如图1所示,取一个圆玻璃瓶,里面盛满水,用穿有透明细管的橡皮塞封口,使水面位于细管中,用手捏玻璃瓶,会看到什么现象?说明什么?
图1
(2)用手压橡皮泥,橡皮泥发生形变;脚踩在松软的土地上,留下了深深的脚印(形变),这两种形变与玻璃瓶的形变有什么不同?
(3)用手拉弹簧,弹簧会对手产生一个拉力(如图2所示),这个拉力是如何产生的?
图2
答案 (1)手捏玻璃瓶,管中水面上升.说明受压时玻璃瓶发生形变,体积变小了.
(2)橡皮泥、泥土受力后发生的形变,在撤去外力后不能恢复原状(非弹性形变),玻璃瓶的形变在撤去外力后能恢复原状(弹性形变).
(3)弹簧受到拉力后发生形变(伸长),发生形变的弹簧要恢复原状,对手就产生了拉力.
[要点提炼]
1.弹性形变和弹力
(1)弹力:发生弹性形变的物体,由于要恢复原状,就会对跟它接触使它发生形变的物体产生力的作用,这种力叫做弹力.
(2)弹性形变:作用在物体上的外力撤去后,物体能恢复原状的形变.
(3)范性形变:外力撤去后,物体不能恢复原状的形变.
2.弹力产生的条件:(1)两物体相互接触;(2)发生弹性形变.
二、胡克定律
[问题设计] 如图3所示,为一弹簧测力计.弹簧测力计的刻度是否均匀?这说明什么?
图3
答案 均匀.说明弹簧测力计的弹力与弹簧的形变量成正比.
[要点提炼]
1.内容:在弹性限度内,弹簧弹力的大小F跟弹簧伸长(或缩短)的长度x成正比.
2.公式:F=kx.
3.说明
(1)应用条件:弹簧发生形变时必须在弹性限度内.
(2)x是弹簧的形变量,而不是弹簧形变后的长度.
(3)k为弹簧的劲度系数,反映弹簧本身的属性,由弹簧自身的长度、粗细、材料等因素决定,与弹力F的大小和伸长量x无关.
(4)F-x图像是一条过原点的倾斜直线(如图4所示),直线的斜率表示弹簧的劲度系数k.
图4
(5)弹簧弹力的变化量ΔF与形变量的变化量Δx也成正比,即ΔF=kΔx.
三、弹力的方向
[问题设计]
1.一铁块放在海绵上,铁块和海绵都发生了形变,从而在它们之间产生了弹力,如图5所示.海绵对铁块的支持力是如何产生的?方向怎样?铁块对海绵的压力是怎样产生的?方向怎样?
图5
答案 (1)海绵对铁块的支持力:海绵发生弹性形变,对与它接触的铁块产生力的作用,方向垂直于接触面向上(如图甲).
甲 乙
(2)铁块对海绵的压力:铁块发生弹性形变,对与它接触的海绵产生力的作用,方向垂直接触面向下(如图乙).
2.如图6所示,用橡皮绳斜向右上拉放在水平面上的物块.橡皮绳对物块的拉力是怎样产生的?方向怎样?
图6
答案 由于橡皮绳发生形变,对与它接触的物块产生力的作用,方向沿绳指向绳收缩的方向(沿绳斜向右上).
[要点提炼]
1.压力、支持力的方向:总是垂直于接触面,若接触面是曲面,则垂直于接触面的切线;若接触面是球面,弹力方向延长线或反向延长线过球心.
2.绳的拉力方向:总是沿着绳并指向绳收缩的方向.
[延伸思考]
如图7所示,把一个球形物体A放在半球形容器B内,在图中画出A受到的弹力.
图7
答案 A受到的弹力垂直于两接触面的切线(弹力方向的延长线过球心),如图所示.
一、弹力的产生
例1 关于弹力的产生,下列说法正确的是( )
A.木块放在桌面上受到一个向上的弹力,这是由于木块发生微小形变而产生的
B.木块放在桌面上,木块没有形变,所以对桌面没有施加弹力
C.拿一根细竹竿拨动水中的木头,木头受到竹竿的弹力,这是由于木头发生形变而产生的
D.挂在电线下面的电灯受到向上的拉力,是因为电线发生微小的形变而产生的
解析 木块和桌面相互作用,都会发生微小的形变.桌面发生微小形变对木块有向上的弹力即支持力;木块由于发生微小形变对桌面有向下的弹力即压力,A、B都错.木头受到的弹力是由细竹竿发生形变而产生的,C错.电灯受到的拉力是电线发生微小形变而产生的,D对.
答案 D
二、弹力的方向
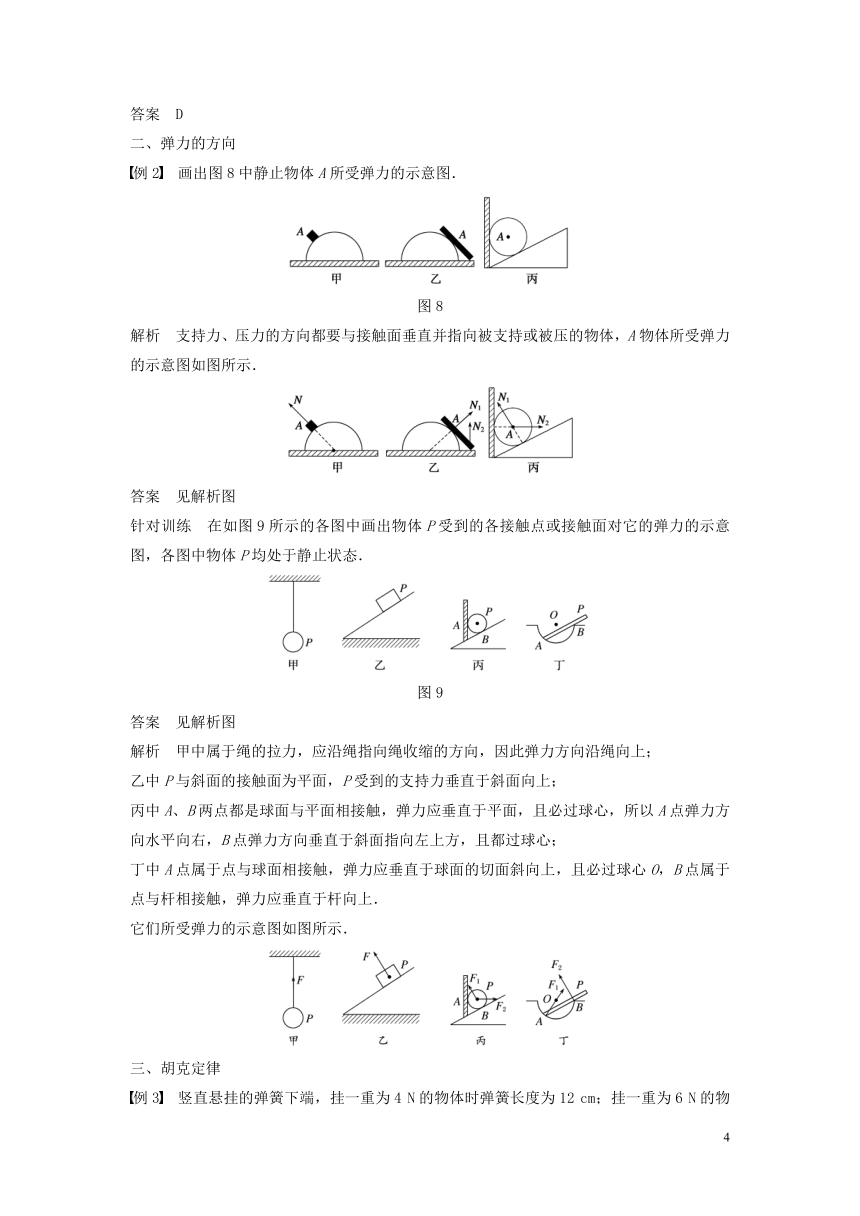
例2 画出图8中静止物体A所受弹力的示意图.
图8
解析 支持力、压力的方向都要与接触面垂直并指向被支持或被压的物体,A物体所受弹力的示意图如图所示.
答案 见解析图
针对训练 在如图9所示的各图中画出物体P受到的各接触点或接触面对它的弹力的示意图,各图中物体P均处于静止状态.
图9
答案 见解析图
解析 甲中属于绳的拉力,应沿绳指向绳收缩的方向,因此弹力方向沿绳向上;
乙中P与斜面的接触面为平面,P受到的支持力垂直于斜面向上;
丙中A、B两点都是球面与平面相接触,弹力应垂直于平面,且必过球心,所以A点弹力方向水平向右,B点弹力方向垂直于斜面指向左上方,且都过球心;
丁中A点属于点与球面相接触,弹力应垂直于球面的切面斜向上,且必过球心O,B点属于点与杆相接触,弹力应垂直于杆向上.
它们所受弹力的示意图如图所示.
三、胡克定律
例3 竖直悬挂的弹簧下端,挂一重为4 N的物体时弹簧长度为12 cm;挂一重为6 N的物体时弹簧长度为13 cm,则弹簧原长为多少?劲度系数为多少?
解析 弹簧下端悬挂物体时弹簧要伸长,由胡克定律知:弹簧的拉力与弹簧伸长量成正比,即F=kx,其中k为劲度系数,x为弹簧伸长量,x在数值上等于弹簧伸长后总长度L减去弹簧原长L0,即x=L-L0.改变悬挂重物的重力,伸长量变化,这样可以列出两个方程,通过方程组可求出弹簧原长和劲度系数.
设弹簧的原长为L0,劲度系数为k,
设挂G1=4 N的重物时弹簧的长度为L1,
挂G2=6 N的重物时弹簧的长度为L2,
则L1=12 cm,L2=13 cm,由胡克定律得:
G1=k(L1-L0)
G2=k(L2-L0)
代入数据解得:L0=10 cm,k=200 N/m
即弹簧原长为10 cm,劲度系数为200 N/m.
答案 10 cm 200 N/m
弹力
1.(弹力的产生)下列有关物体所受的弹力及形变的说法正确的是( )
A.有弹力作用在物体上,物体一定发生形变,撤去此力后,形变完全消失
B.有弹力作用在物体上,物体不一定发生形变
C.弹力作用在硬物体上,物体不发生形变;弹力作用在软物体上,物体才发生形变
D.一切物体受到弹力都要发生形变,撤去弹力后,形变不一定完全消失
答案 D
解析 力是物体间的相互作用,弹力的施力物体和受力物体都会发生形变,故B项错误;发生形变后的物体,当撤去外力后,有些能完全恢复原状,有些不能完全恢复原状,A项错误,D项正确;不管是硬物体还是软物体,只要有弹力作用,都会发生形变,C项错误.
2.(弹力的产生)杂技演员具有高超的技术,如图10所示,他能轻松地顶住从高处落下的缸,关于他顶缸时头顶受到的压力产生的直接原因是( )
图10
A.缸的形变 B.头的形变
C.缸受到重力 D.人受到重力
答案 A
解析 头顶受到的压力的施力物体是缸,受力物体是头顶,头顶受到的压力产生的直接原因是缸的形变,间接原因是缸受到重力,A项正确.
3.(弹力的方向)三个相同的支座上分别放着三个质量和直径均相同的光滑圆球a、b、c,支点P、Q在同一水平面上.a的重心位于球心,b、c的重心分别位于球心的正上方和正下方,如图11所示,三球皆静止,试分析三种情况下支点P、Q对球的弹力方向是怎样的?
图11
答案 见解析
解析 三种情况都是点与点接触,圆球所受弹力的方向都是垂直于接触面指向球心,即沿半径指向球心,如图所示,弹力的方向与重心的位置无关.
4.(胡克定律)由实验测得某弹簧所受弹力F和弹簧的长度L的关系图像如图12所示,求:
图12
(1)该弹簧的原长为多少?
(2)该弹簧的劲度系数为多少?
答案 (1)15 cm (2)500 N/m
解析 解法一:(1)弹簧不产生弹力时的长度等于原长,由题图可知该弹簧的原长为L0=15 cm.
(2)据F=kx得劲度系数:k==,由图线可知,
该弹簧伸长ΔL=(25 cm-15 cm)=10 cm时,
弹力ΔF=50 N.
所以k== N/m=500 N/m.
解法二:根据胡克定律得F=k(L-L0),
代入图像中的两点(0.25,50)和(0.05,-50).
可得50=k(0.25-L0)-50=k(0.05-L0)
解得L0=0.15 m=15 cm,k=500 N/m.
题组一 形变及弹力的产生
1.(多选)下列各种情况中,属于弹性形变的有( )
A.撑竿跳高运动员起跳中,撑竿的形变
B.当你坐在椅子上时,椅面发生的微小形变
C.细钢丝被绕制成弹簧
D.铝桶被砸扁
答案 AB
解析 “撑竿的形变”、“椅面发生的微小形变”均能恢复原状,是弹性形变;“细钢丝被绕制成弹簧”不能恢复原状,“铝桶被砸扁”不能恢复原状,是范性形变.故选项A、B正确,C、D错误.
2.关于弹性形变,下列说法正确的是( )
A.物体形状的改变叫弹性形变
B.一根钢筋用力弯折后的形变就是弹性形变
C.物体在外力停止作用后,能够恢复原来形状的形变,叫弹性形变
D.物体在外力停止作用后的形变,叫弹性形变
答案 C
解析 弹性形变指物体在外力停止作用后,能够恢复原状的形变,C正确,A、D错误;钢筋用力弯折后,无法恢复到原来的形状,不属于弹性形变,B错误.
3.足球运动是目前全球体育界最具影响力的项目之一,深受青少年喜爱.如图1所示为三种与足球有关的情景.下列说法正确的是( )
图1
A.甲图中,静止在草地上的足球受到的弹力就是它的重力
B.乙图中,静止在光滑水平地面上的两个足球由于接触而受到相互作用的弹力
C.丙图中,落在球网中的足球受到弹力是由于足球发生了形变
D.丙图中,落在球网中的足球受到弹力是由于球网发生了形变
答案 D
解析 静止在草地上的足球受到的弹力,与重力相平衡,但不是它的重力,故A错误;静止在光滑水平地面上的两个足球虽然接触,但由于没有弹性形变,所以没有受到相互作用的弹力,B错误;足球撞到网上,球网被撑开,由于球网的形变,而使足球受到了弹力,故C错误,D正确.
题组二 弹力方向的判断
4.体育课上一学生将足球踢向斜台,如图2所示,下列关于足球和斜台作用时斜台给足球的弹力方向的说法正确的是( )
图2
A.沿v1的方向 B.沿v2的方向
C.先沿v1的方向后沿v2的方向 D.沿垂直于斜台斜向左上方的方向
答案 D
解析 足球与斜台的作用是球面与平面的相互作用,足球所受弹力的方向垂直于斜台指向足球,即斜向左上方,故D正确.
5.有四位同学把斜面对物体的支持力,分别画成如图所示的四种情况,其中正确的是( )
答案 A
解析 斜面对物体的支持力作用在物体上,垂直斜面向上,故A正确,B、C、D错误.
6.一杆搁在矮墙上,关于杆受到的弹力的方向,图中画得正确的是( )
答案 D
解析 弹力的方向总是垂直于接触面指向受力物体,D对.
7.在图3中画出物体A所受弹力的示意图.
图3
答案 如图所示
题组三 胡克定律
8.关于弹簧的劲度系数k,下列说法中正确的是( )
A.与弹簧所受的拉力大小有关,拉力越大,k值也越大
B.由弹簧本身决定,与弹簧所受的拉力大小及形变程度无关
C.与弹簧发生的形变的大小有关,形变越大,k值越小
D.与弹簧本身特性、所受拉力的大小、形变程度都无关
答案 B
9.如图4甲、乙所示,弹簧测力计和细线的重力及一切摩擦不计,物重G=1 N,则弹簧测力计A和B的示数分别为( )
图4
A.1 N,0 B.0,1 N C.2 N,1 N D.1 N,1 N
答案 D
解析 题图中弹簧测力计A、B的受力情况是一样的,都是左右两端各受1 N的拉力,此时弹簧测力计的读数都是1 N.D正确.
10.一根轻质弹簧一端固定,用大小为F1的力压弹簧的另一端,平衡时长度为l1;改用大小为F2的力拉弹簧,平衡时长度为l2.弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为( )
A. B. C. D.
答案 C
解析 根据胡克定律有:F1=k(l0-l1),F2=k(l2-l0),由两式可解得:k=,故C正确.
11.一根轻弹簧的伸长量x跟所受的外力F之间的关系图像如图5所示.
图5
(1)求弹簧的劲度系数k;
(2)若弹簧原长l0=60 cm,当把弹簧压缩到40 cm长时,需要多大的压力?
(3)如果用600 N的拉力拉弹簧(仍在弹性限度内,弹簧原长同上),弹簧长度l是多少?
答案 (1)1 500 N/m (2)300 N (3)100 cm
解析 (1)由题图可知当弹簧受外力F1=9×102 N时
弹簧的伸长量x1=0.6 m
故k===1 500 N/m
(2)当把弹簧压缩到40 cm长时,
弹簧的形变量x2=(0.6-0.4) m=0.2 m
弹力为F2=kx2=1 500 N/m×0.2 m=300 N
故需用300 N的压力
(3)由F3=kx3,
得x3===0.4 m=40 cm
故弹簧的长度l=l0+x3=60 cm+40 cm=100 cm
12.有两根相同的轻弹簧a和b,劲度系数均为k,现将它们按如图6甲所示连接,下面挂质量均为m的两个小物体,此时两根轻弹簧总长为l.若将两个物体按图乙所示方法挂在两轻弹簧上,则两根轻弹簧的总长为多少?(重力加速度为g)
图6
答案 l-
解析 设弹簧的原长为l0,则根据胡克定律可得,按题图甲所示连接时,两轻弹簧的伸长量为Δla1=Δlb1=,所以有l=2l0+
按题图乙所示连接时,两轻弹簧的伸长量分别为
Δla2=,Δlb2=
两根轻弹簧总长为:l2=2l0+=l-
[目标定位] 1.知道形变的概念,并会区分某种形变是弹性形变还是非弹性形变.2.知道弹力的定义及产生的条件,会判断两个物体间是否存在弹力,并会判断弹力的方向.3.掌握胡克定律并能用此定律解决有关问题.
一、形变和弹力
[问题设计]
(1)如图1所示,取一个圆玻璃瓶,里面盛满水,用穿有透明细管的橡皮塞封口,使水面位于细管中,用手捏玻璃瓶,会看到什么现象?说明什么?
图1
(2)用手压橡皮泥,橡皮泥发生形变;脚踩在松软的土地上,留下了深深的脚印(形变),这两种形变与玻璃瓶的形变有什么不同?
(3)用手拉弹簧,弹簧会对手产生一个拉力(如图2所示),这个拉力是如何产生的?
图2
答案 (1)手捏玻璃瓶,管中水面上升.说明受压时玻璃瓶发生形变,体积变小了.
(2)橡皮泥、泥土受力后发生的形变,在撤去外力后不能恢复原状(非弹性形变),玻璃瓶的形变在撤去外力后能恢复原状(弹性形变).
(3)弹簧受到拉力后发生形变(伸长),发生形变的弹簧要恢复原状,对手就产生了拉力.
[要点提炼]
1.弹性形变和弹力
(1)弹力:发生弹性形变的物体,由于要恢复原状,就会对跟它接触使它发生形变的物体产生力的作用,这种力叫做弹力.
(2)弹性形变:作用在物体上的外力撤去后,物体能恢复原状的形变.
(3)范性形变:外力撤去后,物体不能恢复原状的形变.
2.弹力产生的条件:(1)两物体相互接触;(2)发生弹性形变.
二、胡克定律
[问题设计] 如图3所示,为一弹簧测力计.弹簧测力计的刻度是否均匀?这说明什么?
图3
答案 均匀.说明弹簧测力计的弹力与弹簧的形变量成正比.
[要点提炼]
1.内容:在弹性限度内,弹簧弹力的大小F跟弹簧伸长(或缩短)的长度x成正比.
2.公式:F=kx.
3.说明
(1)应用条件:弹簧发生形变时必须在弹性限度内.
(2)x是弹簧的形变量,而不是弹簧形变后的长度.
(3)k为弹簧的劲度系数,反映弹簧本身的属性,由弹簧自身的长度、粗细、材料等因素决定,与弹力F的大小和伸长量x无关.
(4)F-x图像是一条过原点的倾斜直线(如图4所示),直线的斜率表示弹簧的劲度系数k.
图4
(5)弹簧弹力的变化量ΔF与形变量的变化量Δx也成正比,即ΔF=kΔx.
三、弹力的方向
[问题设计]
1.一铁块放在海绵上,铁块和海绵都发生了形变,从而在它们之间产生了弹力,如图5所示.海绵对铁块的支持力是如何产生的?方向怎样?铁块对海绵的压力是怎样产生的?方向怎样?
图5
答案 (1)海绵对铁块的支持力:海绵发生弹性形变,对与它接触的铁块产生力的作用,方向垂直于接触面向上(如图甲).
甲 乙
(2)铁块对海绵的压力:铁块发生弹性形变,对与它接触的海绵产生力的作用,方向垂直接触面向下(如图乙).
2.如图6所示,用橡皮绳斜向右上拉放在水平面上的物块.橡皮绳对物块的拉力是怎样产生的?方向怎样?
图6
答案 由于橡皮绳发生形变,对与它接触的物块产生力的作用,方向沿绳指向绳收缩的方向(沿绳斜向右上).
[要点提炼]
1.压力、支持力的方向:总是垂直于接触面,若接触面是曲面,则垂直于接触面的切线;若接触面是球面,弹力方向延长线或反向延长线过球心.
2.绳的拉力方向:总是沿着绳并指向绳收缩的方向.
[延伸思考]
如图7所示,把一个球形物体A放在半球形容器B内,在图中画出A受到的弹力.
图7
答案 A受到的弹力垂直于两接触面的切线(弹力方向的延长线过球心),如图所示.
一、弹力的产生
例1 关于弹力的产生,下列说法正确的是( )
A.木块放在桌面上受到一个向上的弹力,这是由于木块发生微小形变而产生的
B.木块放在桌面上,木块没有形变,所以对桌面没有施加弹力
C.拿一根细竹竿拨动水中的木头,木头受到竹竿的弹力,这是由于木头发生形变而产生的
D.挂在电线下面的电灯受到向上的拉力,是因为电线发生微小的形变而产生的
解析 木块和桌面相互作用,都会发生微小的形变.桌面发生微小形变对木块有向上的弹力即支持力;木块由于发生微小形变对桌面有向下的弹力即压力,A、B都错.木头受到的弹力是由细竹竿发生形变而产生的,C错.电灯受到的拉力是电线发生微小形变而产生的,D对.
答案 D
二、弹力的方向
例2 画出图8中静止物体A所受弹力的示意图.
图8
解析 支持力、压力的方向都要与接触面垂直并指向被支持或被压的物体,A物体所受弹力的示意图如图所示.
答案 见解析图
针对训练 在如图9所示的各图中画出物体P受到的各接触点或接触面对它的弹力的示意图,各图中物体P均处于静止状态.
图9
答案 见解析图
解析 甲中属于绳的拉力,应沿绳指向绳收缩的方向,因此弹力方向沿绳向上;
乙中P与斜面的接触面为平面,P受到的支持力垂直于斜面向上;
丙中A、B两点都是球面与平面相接触,弹力应垂直于平面,且必过球心,所以A点弹力方向水平向右,B点弹力方向垂直于斜面指向左上方,且都过球心;
丁中A点属于点与球面相接触,弹力应垂直于球面的切面斜向上,且必过球心O,B点属于点与杆相接触,弹力应垂直于杆向上.
它们所受弹力的示意图如图所示.
三、胡克定律
例3 竖直悬挂的弹簧下端,挂一重为4 N的物体时弹簧长度为12 cm;挂一重为6 N的物体时弹簧长度为13 cm,则弹簧原长为多少?劲度系数为多少?
解析 弹簧下端悬挂物体时弹簧要伸长,由胡克定律知:弹簧的拉力与弹簧伸长量成正比,即F=kx,其中k为劲度系数,x为弹簧伸长量,x在数值上等于弹簧伸长后总长度L减去弹簧原长L0,即x=L-L0.改变悬挂重物的重力,伸长量变化,这样可以列出两个方程,通过方程组可求出弹簧原长和劲度系数.
设弹簧的原长为L0,劲度系数为k,
设挂G1=4 N的重物时弹簧的长度为L1,
挂G2=6 N的重物时弹簧的长度为L2,
则L1=12 cm,L2=13 cm,由胡克定律得:
G1=k(L1-L0)
G2=k(L2-L0)
代入数据解得:L0=10 cm,k=200 N/m
即弹簧原长为10 cm,劲度系数为200 N/m.
答案 10 cm 200 N/m
弹力
1.(弹力的产生)下列有关物体所受的弹力及形变的说法正确的是( )
A.有弹力作用在物体上,物体一定发生形变,撤去此力后,形变完全消失
B.有弹力作用在物体上,物体不一定发生形变
C.弹力作用在硬物体上,物体不发生形变;弹力作用在软物体上,物体才发生形变
D.一切物体受到弹力都要发生形变,撤去弹力后,形变不一定完全消失
答案 D
解析 力是物体间的相互作用,弹力的施力物体和受力物体都会发生形变,故B项错误;发生形变后的物体,当撤去外力后,有些能完全恢复原状,有些不能完全恢复原状,A项错误,D项正确;不管是硬物体还是软物体,只要有弹力作用,都会发生形变,C项错误.
2.(弹力的产生)杂技演员具有高超的技术,如图10所示,他能轻松地顶住从高处落下的缸,关于他顶缸时头顶受到的压力产生的直接原因是( )
图10
A.缸的形变 B.头的形变
C.缸受到重力 D.人受到重力
答案 A
解析 头顶受到的压力的施力物体是缸,受力物体是头顶,头顶受到的压力产生的直接原因是缸的形变,间接原因是缸受到重力,A项正确.
3.(弹力的方向)三个相同的支座上分别放着三个质量和直径均相同的光滑圆球a、b、c,支点P、Q在同一水平面上.a的重心位于球心,b、c的重心分别位于球心的正上方和正下方,如图11所示,三球皆静止,试分析三种情况下支点P、Q对球的弹力方向是怎样的?
图11
答案 见解析
解析 三种情况都是点与点接触,圆球所受弹力的方向都是垂直于接触面指向球心,即沿半径指向球心,如图所示,弹力的方向与重心的位置无关.
4.(胡克定律)由实验测得某弹簧所受弹力F和弹簧的长度L的关系图像如图12所示,求:
图12
(1)该弹簧的原长为多少?
(2)该弹簧的劲度系数为多少?
答案 (1)15 cm (2)500 N/m
解析 解法一:(1)弹簧不产生弹力时的长度等于原长,由题图可知该弹簧的原长为L0=15 cm.
(2)据F=kx得劲度系数:k==,由图线可知,
该弹簧伸长ΔL=(25 cm-15 cm)=10 cm时,
弹力ΔF=50 N.
所以k== N/m=500 N/m.
解法二:根据胡克定律得F=k(L-L0),
代入图像中的两点(0.25,50)和(0.05,-50).
可得50=k(0.25-L0)-50=k(0.05-L0)
解得L0=0.15 m=15 cm,k=500 N/m.
题组一 形变及弹力的产生
1.(多选)下列各种情况中,属于弹性形变的有( )
A.撑竿跳高运动员起跳中,撑竿的形变
B.当你坐在椅子上时,椅面发生的微小形变
C.细钢丝被绕制成弹簧
D.铝桶被砸扁
答案 AB
解析 “撑竿的形变”、“椅面发生的微小形变”均能恢复原状,是弹性形变;“细钢丝被绕制成弹簧”不能恢复原状,“铝桶被砸扁”不能恢复原状,是范性形变.故选项A、B正确,C、D错误.
2.关于弹性形变,下列说法正确的是( )
A.物体形状的改变叫弹性形变
B.一根钢筋用力弯折后的形变就是弹性形变
C.物体在外力停止作用后,能够恢复原来形状的形变,叫弹性形变
D.物体在外力停止作用后的形变,叫弹性形变
答案 C
解析 弹性形变指物体在外力停止作用后,能够恢复原状的形变,C正确,A、D错误;钢筋用力弯折后,无法恢复到原来的形状,不属于弹性形变,B错误.
3.足球运动是目前全球体育界最具影响力的项目之一,深受青少年喜爱.如图1所示为三种与足球有关的情景.下列说法正确的是( )
图1
A.甲图中,静止在草地上的足球受到的弹力就是它的重力
B.乙图中,静止在光滑水平地面上的两个足球由于接触而受到相互作用的弹力
C.丙图中,落在球网中的足球受到弹力是由于足球发生了形变
D.丙图中,落在球网中的足球受到弹力是由于球网发生了形变
答案 D
解析 静止在草地上的足球受到的弹力,与重力相平衡,但不是它的重力,故A错误;静止在光滑水平地面上的两个足球虽然接触,但由于没有弹性形变,所以没有受到相互作用的弹力,B错误;足球撞到网上,球网被撑开,由于球网的形变,而使足球受到了弹力,故C错误,D正确.
题组二 弹力方向的判断
4.体育课上一学生将足球踢向斜台,如图2所示,下列关于足球和斜台作用时斜台给足球的弹力方向的说法正确的是( )
图2
A.沿v1的方向 B.沿v2的方向
C.先沿v1的方向后沿v2的方向 D.沿垂直于斜台斜向左上方的方向
答案 D
解析 足球与斜台的作用是球面与平面的相互作用,足球所受弹力的方向垂直于斜台指向足球,即斜向左上方,故D正确.
5.有四位同学把斜面对物体的支持力,分别画成如图所示的四种情况,其中正确的是( )
答案 A
解析 斜面对物体的支持力作用在物体上,垂直斜面向上,故A正确,B、C、D错误.
6.一杆搁在矮墙上,关于杆受到的弹力的方向,图中画得正确的是( )
答案 D
解析 弹力的方向总是垂直于接触面指向受力物体,D对.
7.在图3中画出物体A所受弹力的示意图.
图3
答案 如图所示
题组三 胡克定律
8.关于弹簧的劲度系数k,下列说法中正确的是( )
A.与弹簧所受的拉力大小有关,拉力越大,k值也越大
B.由弹簧本身决定,与弹簧所受的拉力大小及形变程度无关
C.与弹簧发生的形变的大小有关,形变越大,k值越小
D.与弹簧本身特性、所受拉力的大小、形变程度都无关
答案 B
9.如图4甲、乙所示,弹簧测力计和细线的重力及一切摩擦不计,物重G=1 N,则弹簧测力计A和B的示数分别为( )
图4
A.1 N,0 B.0,1 N C.2 N,1 N D.1 N,1 N
答案 D
解析 题图中弹簧测力计A、B的受力情况是一样的,都是左右两端各受1 N的拉力,此时弹簧测力计的读数都是1 N.D正确.
10.一根轻质弹簧一端固定,用大小为F1的力压弹簧的另一端,平衡时长度为l1;改用大小为F2的力拉弹簧,平衡时长度为l2.弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为( )
A. B. C. D.
答案 C
解析 根据胡克定律有:F1=k(l0-l1),F2=k(l2-l0),由两式可解得:k=,故C正确.
11.一根轻弹簧的伸长量x跟所受的外力F之间的关系图像如图5所示.
图5
(1)求弹簧的劲度系数k;
(2)若弹簧原长l0=60 cm,当把弹簧压缩到40 cm长时,需要多大的压力?
(3)如果用600 N的拉力拉弹簧(仍在弹性限度内,弹簧原长同上),弹簧长度l是多少?
答案 (1)1 500 N/m (2)300 N (3)100 cm
解析 (1)由题图可知当弹簧受外力F1=9×102 N时
弹簧的伸长量x1=0.6 m
故k===1 500 N/m
(2)当把弹簧压缩到40 cm长时,
弹簧的形变量x2=(0.6-0.4) m=0.2 m
弹力为F2=kx2=1 500 N/m×0.2 m=300 N
故需用300 N的压力
(3)由F3=kx3,
得x3===0.4 m=40 cm
故弹簧的长度l=l0+x3=60 cm+40 cm=100 cm
12.有两根相同的轻弹簧a和b,劲度系数均为k,现将它们按如图6甲所示连接,下面挂质量均为m的两个小物体,此时两根轻弹簧总长为l.若将两个物体按图乙所示方法挂在两轻弹簧上,则两根轻弹簧的总长为多少?(重力加速度为g)
图6
答案 l-
解析 设弹簧的原长为l0,则根据胡克定律可得,按题图甲所示连接时,两轻弹簧的伸长量为Δla1=Δlb1=,所以有l=2l0+
按题图乙所示连接时,两轻弹簧的伸长量分别为
Δla2=,Δlb2=
两根轻弹簧总长为:l2=2l0+=l-
同课章节目录
- 开篇 激动人心的万千体验
- 01物理学——理性的追求
- 02物理学——人类文明的奇葩
- 03学物理——探究求真
- 第一章 怎样描述物体的运动
- 1 走近运动
- 2 怎样描述运动的快慢
- 3 怎样描述运动的快慢(续)
- 4 怎样描述速度变化的快慢
- 第二章 研究匀变速直线运动的规律
- 1 伽利略对落体运动的研究
- 2 自由落体运动的规律
- 3 匀变速直线运动的规律
- 4 匀变速直线运动规律的应用
- 第三章 力与相互作用
- 1 牛顿第三定律
- 2 弹力
- 3 摩擦力
- 4 分析物体的受力
- 第四章 怎样求合力与分力
- 1 怎样求合力
- 2 怎样分解力
- 3 共点力的平衡及其应用
- 第五章 研究力和运动的关系
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿运动定律的案例分析
- 5 超重与失重
