数学一年级上北师大版7古人计数教学设计1
文档属性
| 名称 | 数学一年级上北师大版7古人计数教学设计1 |
|
|
| 格式 | zip | ||
| 文件大小 | 873.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-02 00:00:00 | ||
图片预览



文档简介
《古人计数》教学设计1
教学内容
本册教科书第74-76页“古人计数”。
教学内容分析
学习20以内数的加减法是从这一节“古人计数”开始的。首先要把数的范围从10以内拓展到20以内,数扩充了,却不需要增加表示数的符号。用有限的符号表示无穷的数,是古人奇妙的发明和了不起的智慧。
“古人计数”(第1课时)的情境问题串有三个数学活动。
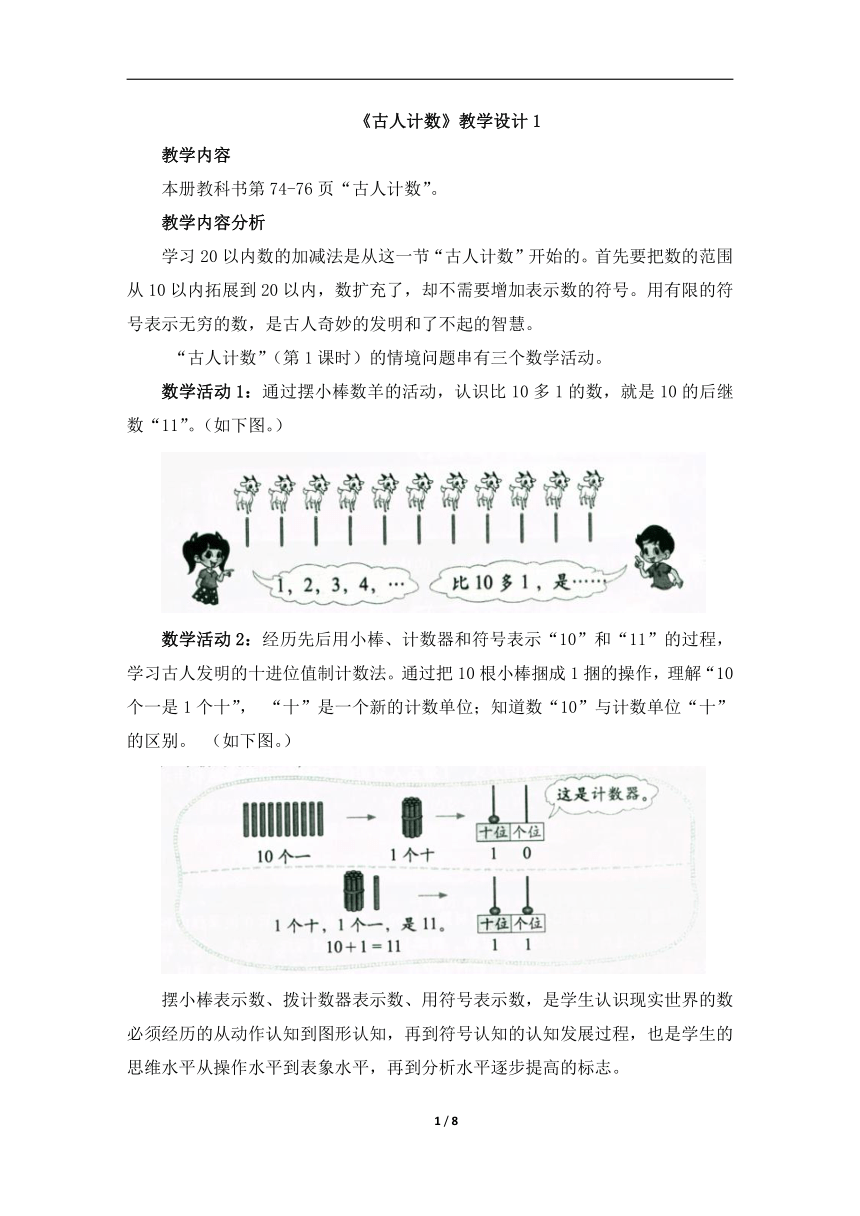
数学活动1:通过摆小棒数羊的活动,认识比10多1的数,就是10的后继数“11”。(如下图。)
数学活动2:经历先后用小棒、计数器和符号表示“10”和“11”的过程,学习古人发明的十进位值制计数法。通过把10根小棒捆成1捆的操作,理解“10个一是1个十”, “十”是一个新的计数单位;知道数“10”与计数单位“十”的区别。 (如下图。)
摆小棒表示数、拨计数器表示数、用符号表示数,是学生认识现实世界的数必须经历的从动作认知到图形认知,再到符号认知的认知发展过程,也是学生的思维水平从操作水平到表象水平,再到分析水平逐步提高的标志。
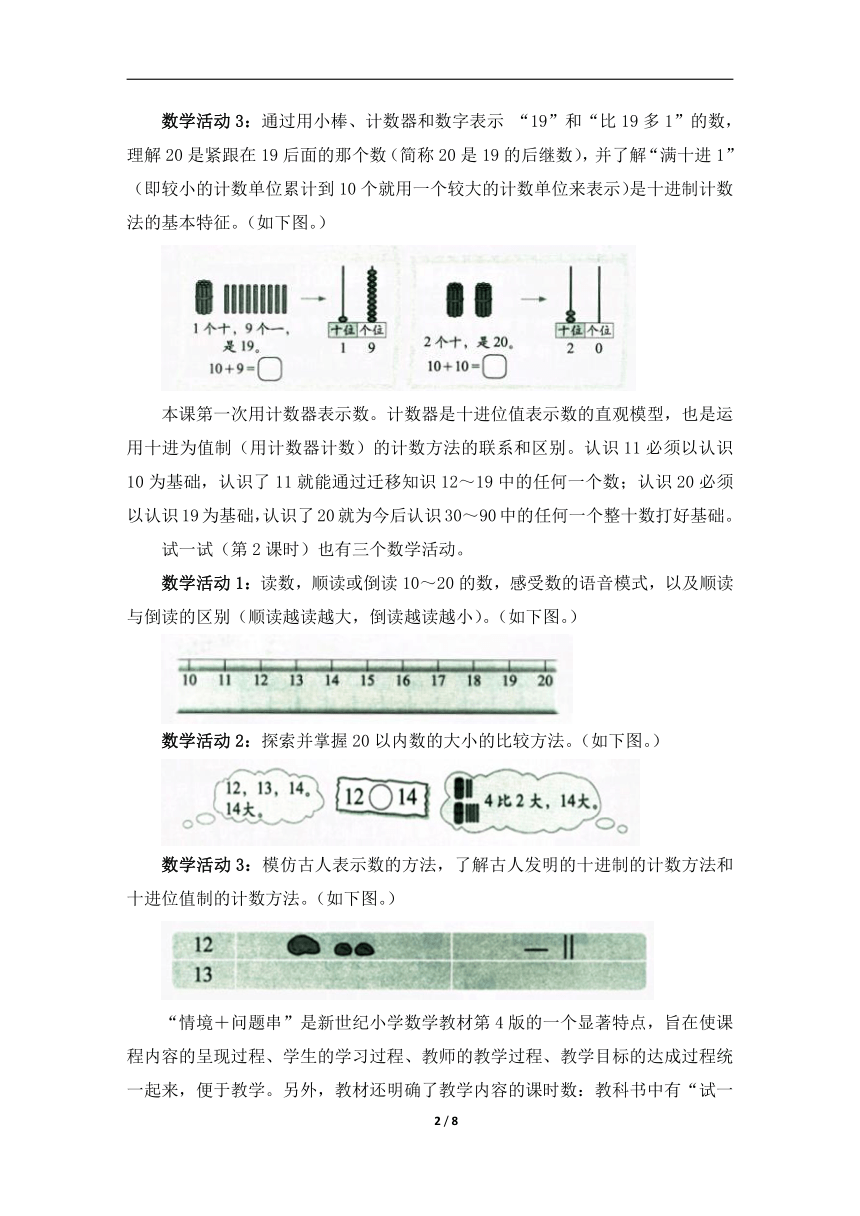
数学活动3:通过用小棒、计数器和数字表示 “19”和“比19多1”的数,理解20是紧跟在19后面的那个数(简称20是19的后继数),并了解“满十进1”(即较小的计数单位累计到10个就用一个较大的计数单位来表示)是十进制计数法的基本特征。(如下图。)
本课第一次用计数器表示数。计数器是十进位值表示数的直观模型,也是运用十进为值制(用计数器计数)的计数方法的联系和区别。认识11必须以认识10为基础,认识了11就能通过迁移知识12~19中的任何一个数;认识20必须以认识19为基础,认识了20就为今后认识30~90中的任何一个整十数打好基础。
试一试(第2课时)也有三个数学活动。
数学活动1:读数,顺读或倒读10~20的数,感受数的语音模式,以及顺读与倒读的区别(顺读越读越大,倒读越读越小)。(如下图。)
数学活动2:探索并掌握20以内数的大小的比较方法。(如下图。)
数学活动3:模仿古人表示数的方法,了解古人发明的十进制的计数方法和十进位值制的计数方法。(如下图。)
“情境+问题串”是新世纪小学数学教材第4版的一个显著特点,旨在使课程内容的呈现过程、学生的学习过程、教师的教学过程、教学目标的达成过程统一起来,便于教学。另外,教材还明确了教学内容的课时数:教科书中有“试一试”栏目的,都是2课时;“试一试”是第2课时的学习内容。
第1课时教学设计
一、学习目标
1.结合具体情境,体会20以内的数的意义,能认、读、写20以内的数。
2.会用小棒和计数器直观表示10~20的数,初步了解十进制的计数方法与十进位值制的计数方法的主要特征,能说出个位、十位上的数字表示的意义。
3.积极参与数学活动,对数学有好奇心和求知欲。
二、教具准备
教师和每个学生都准备20根小棒,2根橡皮筋,1个计数器。
三、过程预设
观察教科书第74页的情境图。坐在羊圈旁的牧羊人在做什么?让学生解读情境图。(如下图。)
牧羊人用石子表示羊,他摆出3个石子,恰好表示跑出羊圈的3只羊。原来牧羊人在摆石子数羊。
活动1:每个学生都用小棒代表羊,摆一摆、数一数,牧羊人一共有多少只羊?要做到不多数也不少数,既不重复也不遗漏。
请学生说一说:
(1)一共有多少只?(教师板书:十一。)
(2)羊的只数与学过的数10有什么关系?(教师板书:比10多1。)
(3)用什么数字表示羊的只数?(教师板书:11。)
讲解:数词“十一”是羊的只数的语音形式,数字“11”是羊的只数的书写形式,11是比10多1的数,像10是紧跟在9后面的数一样,11是紧跟在10后面的数。
古人是怎么发明书写比10大的数的方法的?
活动2:经历从直观到抽象表示羊的只数的数学化过程。
(1)请学生跟着老师一起做:数出10小棒,用橡皮筋把它们捆成1捆。并讨论:1捆小棒与1根小棒有什么区别。
讲解:1捆小棒与1根小棒的粗细不同,形态不同。用1捆小棒表示1个“十”,1根小棒表示1个“一”,一眼就能看明白。而“1捆小棒”就是我们要学习和掌握的一个新的计数单位——“十”。
接着,教师介绍并演示:怎样在计数器上表示计数单位“十”?并要求学生跟着操作。
在计数器的个位上先拨出9颗珠子,表示9,再添1颗珠子。个位上的10颗珠子表示 “10个一”,是10;在十位上的1颗珠子,表示“1个十”;十位上的1颗珠子可以取代个位上的10颗珠子。所以,10可以简单地用十位上的1颗珠子表示。
数10与计数单位“十”在意义上的区别:数10是9的后继数(即紧跟在9后面的数,简称9的后继数),而计数单位“十”表示“10个一”。
(2)请学生分别用小棒和计数器表示数“11”。
想一想,说一说:用小棒表示11(1捆加1根)和用计数器表示11(个位与十位上分别拨1个珠子)有什么相同与不同的地方?
相同点:都用到两种计数单位:“十”与“一”;都有1个十,1个一,是11。
不同点:用小棒表示11时,是用形态不同的1捆和1根小棒来区别“十”与“一”;不论它们放置的位置如何,都表示11。用计数器表示11时,只用形态相同的2颗珠子,是通过珠子的不同位置来区别“十”与“一”的。
讲解:用小棒表示数的方法是十进制的计数方法,用计数器表示数的方法是十进位值制的计数方法。“10个一是1个十”是十进制计数方法的主要特征;珠子或数字处在不同的位置表示不同的数值是位值制计数方法的主要特征。
活动3:初步了解十进制的“满十进1”的计数法则与位值制的计数方法。
(1)请学生分别用小棒、计数器和数字三种方法表示19。通过交流,明确:
① 摆1捆小棒加9根小棒,即“1个十,9个1,是19”。
②在计数器的十位上拨1颗珠子,个位上拨9颗珠子,是19。
③把计数器上表示的数抽象化,就是数的书写形式——数字19。
(2)请学生继续用上述三种方法表示比“19多1”的数。
通过展示交流,理解20是19的后继数。
①以小棒表示的19为基础,再添人1根小棒;把分散的10根小棒捆成1捆;说明“比19多l”的数是“2个十,是20”。
②以计数器表示的19为基础,在个位上再加1颗珠子,个位上的10颗珠子表示10个 “一”,相当于十位上的1颗珠子表示的1个十。所以,可以在十位上添上1颗珠子,取代个位上的10颗珠子。这时,十位上有2颗珠子,个位上没有珠子,即“2个十,是20”。
告诉学生,当较小的计数单位(“个”)累计到10个时,就用1个较大的计数单位(“十”)取而代之,是十进制计数法的计数法则,这个法则可以简称为“满十进1”。
四、课堂练习
教科书第75页第1,2题;第76页第5,6,8题。(可以直接写在书上。)
第2题的要求是在计数器的档上画出珠子,直观表示给出的数。
第8题要在看懂淘气和笑笑怎么分析18这个数的基础上,换一个数(如15)再分析它。
如果时间允许,可以让小组讨论第1题看图写数:哪些图是十进制计数方法?哪些是十进位值制计数方法?(除计数器表示数是十进位值制的计数方法外,其余都只是十进制的计数方法)
五、课堂小结
先让学生说一说,这节课给自己留下最深的印象是什么?
教师可小结:今天我们对数的认识,从10以内拓展到20以内,认识的数多了10个,但表示数的符号还是10个,没有增加。这是为什么呢?因为同一个数字在不同的数位上表示不同的数值,所以,用较少的数字符号可以表示很多的数,位值制的智慧与优越性就在这里。
第2课时教学设计
一、学习目标
在实现第1课时三个学习目标的基础上,再达成如下一个学习目标:
认识20以内数的有序性,探索并掌握20以内数比较大小的方法。
二、过程预设
活动1:读标有O~20的刻度尺。
每个人自由地读尺子上的数。先从O读到10,稍停,继续读到20,再从20倒着读到10。
思考以下问题。
(1)从O读到10与从10继续读到20,你有什么感受或发现?
从0~10与从10~20都包含11个数。不仅从数的书写形式上有规律(后者比前者在十位上多个1),而且从听觉上也有一种周而复始的重复感。
(2)从10读到20,与从20读到10,两者有什么区别?
读数的顺序不同。从10读到20是顺着读,越读越大;从20读到10是倒着读,越读越小。
活动2:比一比12与14,谁大?谁小?
独立思考,解决上述比较大小的问题,再展示交流。
方法1:从12开始,要顺着数才能数到14,所以14比12大。
方法2:12的直观形式——1捆小棒加2根小棒;14的直观形式——1捆小棒加4根小棒。4根小棒比2根多,所以14比12大。
方法3:12=10+2,14=10+4,因为4>2,所以14>12。
讲解:方法1和方法3的共同特征是能够摆脱数的直观形式,直接用抽象的数字进行思考,所以思维水平都比较高。方法2是方法3的直观背景,方法3是方法2的符号表达;方法3是在分析数的结构的基础上,由已知推出未知。
本题还有如下的一种由已知推出未知的方法:
方法4:14>13,13>12,所以,14>12。其直观背景是:14根小棒比13根多,13根比12根多,所以14根小棒比12根多。
对于一年级小学生,方法3或方法4只要求能够结合直观背景加以理解即可。但教师应该知道方法3与方法4的数学背景:方法3是根据不等式的基本性质(不等式的加法单调性),方法4则是根据大于关系的传递性。
活动3:模仿古人用石子或算筹(小棒)表示12的方式表示13。
独立思考并解答,教师反馈正确答案。
反思:用摆石子的方式表示数与用算筹表示数,有什么区别?
讲解:用石子表示数是十进制的计数方法,它所表示的数与大石子或小石子的位置无关;用算筹表示数是十进位值制的计数方法,用算筹表示数还有个规定:个位上的数摆成纵式,十位上的数摆成横式,纵横交错。十进制的计数方法与十进位值制的计数方法,两者明显的区别是,十进制的计数方法需要用不同特征(如捆或根、大或小)的事物表示“十”或“一”等计数单位;而十进位值制的计数方法,只要用相同的事物(如珠子或算筹)摆在不同的位置来表示不同的计数单位。
三、课堂练习
教科书第76页第3,4,7,9题。
第4题,比较11与7的大小,也可以由已知推出未知:11>10,10>7,所以11>7。
四、课堂小结
本课的重点是通过探索20以内数比较大小的方法,认识20以内数的有序性,并能比较20以内数的大小。通过学习“古人计数”,掌握用小棒或计数器等计数工具表示数的方法。用直观形式表示数,目的是把抽象的数变成可以触摸、可操作的思维对象,为进一步学习数的加减法的直观运算打基础。
实施要求
1.每一个数学活动的教学设计,都包括两个基本要素:①要学生做什么?②要学生想什么?对做的事情的思考,即反思。教学设计不是为了灌输,而是为了导出;教师要在组织、引导学生的探索中去倾听学生自己的解释。课堂教学是否精彩,要看学生有没有产生自己的思想和体验。
2.要明确每一个数学活动的思维对象,即通过数学活动要揭示(发现、掌握)的新的、未知的东西是什么。有些新的、未知的东西,学生自己能够发现,如通过数数可以知道牧羊人一共有多少只羊,也可能知道表示“十一”的数字是11,但学生不可能发现新的计数单位“十”,也不可能发明十进位值制计数法。所以,对于学生不可能独立探究的学习内容,必须依靠有意义的接受式学习。教师必须通过讲解帮助学生理解和掌握新的知识,防止为探究而探究,杜绝没有意义、浪费时间的假探究。
3.遵循学生学习数学的心理规律进行教学。夸美纽斯认为,教一个活动最好的方法是演示。维果茨基认为,在最近发展区的框架内,模仿也具有建构的意义。第1课时活动2的第一个环节(学习计数单位“十”)就包括教师的演示和学生的模仿。弗赖登塔尔认为,学一个活动最好的方法是做。第1课时活动2的第二个环节就是让学生相对独立地做数学,引导学生做的过程,是以布鲁纳的儿童认知发展的理论为根据的:从动作认知,到图形认知,再到符号认知。
4.课堂练习是每堂课学生相对独立的学习阶段,教师要放手让学生独立思考,独立作业。只有经过相对独立学习的发展过程,才可能达到完全独立掌握知识的目的,这是一条规律。在练习前,教师有责任帮助学生理解问题,明确练习的要求(如说明第2题“做一做”是做什么,第8题“说一说”要说什么)。在学生练习的过程中,教师不要随意打断学生的思维,要积极巡视,进行个别指导和帮助,并了解练习中比较普遍存在的问题、错误、困难和差异,以便课后反思,并在下一节课进行更有针对性的教学。
教学内容
本册教科书第74-76页“古人计数”。
教学内容分析
学习20以内数的加减法是从这一节“古人计数”开始的。首先要把数的范围从10以内拓展到20以内,数扩充了,却不需要增加表示数的符号。用有限的符号表示无穷的数,是古人奇妙的发明和了不起的智慧。
“古人计数”(第1课时)的情境问题串有三个数学活动。
数学活动1:通过摆小棒数羊的活动,认识比10多1的数,就是10的后继数“11”。(如下图。)
数学活动2:经历先后用小棒、计数器和符号表示“10”和“11”的过程,学习古人发明的十进位值制计数法。通过把10根小棒捆成1捆的操作,理解“10个一是1个十”, “十”是一个新的计数单位;知道数“10”与计数单位“十”的区别。 (如下图。)
摆小棒表示数、拨计数器表示数、用符号表示数,是学生认识现实世界的数必须经历的从动作认知到图形认知,再到符号认知的认知发展过程,也是学生的思维水平从操作水平到表象水平,再到分析水平逐步提高的标志。
数学活动3:通过用小棒、计数器和数字表示 “19”和“比19多1”的数,理解20是紧跟在19后面的那个数(简称20是19的后继数),并了解“满十进1”(即较小的计数单位累计到10个就用一个较大的计数单位来表示)是十进制计数法的基本特征。(如下图。)
本课第一次用计数器表示数。计数器是十进位值表示数的直观模型,也是运用十进为值制(用计数器计数)的计数方法的联系和区别。认识11必须以认识10为基础,认识了11就能通过迁移知识12~19中的任何一个数;认识20必须以认识19为基础,认识了20就为今后认识30~90中的任何一个整十数打好基础。
试一试(第2课时)也有三个数学活动。
数学活动1:读数,顺读或倒读10~20的数,感受数的语音模式,以及顺读与倒读的区别(顺读越读越大,倒读越读越小)。(如下图。)
数学活动2:探索并掌握20以内数的大小的比较方法。(如下图。)
数学活动3:模仿古人表示数的方法,了解古人发明的十进制的计数方法和十进位值制的计数方法。(如下图。)
“情境+问题串”是新世纪小学数学教材第4版的一个显著特点,旨在使课程内容的呈现过程、学生的学习过程、教师的教学过程、教学目标的达成过程统一起来,便于教学。另外,教材还明确了教学内容的课时数:教科书中有“试一试”栏目的,都是2课时;“试一试”是第2课时的学习内容。
第1课时教学设计
一、学习目标
1.结合具体情境,体会20以内的数的意义,能认、读、写20以内的数。
2.会用小棒和计数器直观表示10~20的数,初步了解十进制的计数方法与十进位值制的计数方法的主要特征,能说出个位、十位上的数字表示的意义。
3.积极参与数学活动,对数学有好奇心和求知欲。
二、教具准备
教师和每个学生都准备20根小棒,2根橡皮筋,1个计数器。
三、过程预设
观察教科书第74页的情境图。坐在羊圈旁的牧羊人在做什么?让学生解读情境图。(如下图。)
牧羊人用石子表示羊,他摆出3个石子,恰好表示跑出羊圈的3只羊。原来牧羊人在摆石子数羊。
活动1:每个学生都用小棒代表羊,摆一摆、数一数,牧羊人一共有多少只羊?要做到不多数也不少数,既不重复也不遗漏。
请学生说一说:
(1)一共有多少只?(教师板书:十一。)
(2)羊的只数与学过的数10有什么关系?(教师板书:比10多1。)
(3)用什么数字表示羊的只数?(教师板书:11。)
讲解:数词“十一”是羊的只数的语音形式,数字“11”是羊的只数的书写形式,11是比10多1的数,像10是紧跟在9后面的数一样,11是紧跟在10后面的数。
古人是怎么发明书写比10大的数的方法的?
活动2:经历从直观到抽象表示羊的只数的数学化过程。
(1)请学生跟着老师一起做:数出10小棒,用橡皮筋把它们捆成1捆。并讨论:1捆小棒与1根小棒有什么区别。
讲解:1捆小棒与1根小棒的粗细不同,形态不同。用1捆小棒表示1个“十”,1根小棒表示1个“一”,一眼就能看明白。而“1捆小棒”就是我们要学习和掌握的一个新的计数单位——“十”。
接着,教师介绍并演示:怎样在计数器上表示计数单位“十”?并要求学生跟着操作。
在计数器的个位上先拨出9颗珠子,表示9,再添1颗珠子。个位上的10颗珠子表示 “10个一”,是10;在十位上的1颗珠子,表示“1个十”;十位上的1颗珠子可以取代个位上的10颗珠子。所以,10可以简单地用十位上的1颗珠子表示。
数10与计数单位“十”在意义上的区别:数10是9的后继数(即紧跟在9后面的数,简称9的后继数),而计数单位“十”表示“10个一”。
(2)请学生分别用小棒和计数器表示数“11”。
想一想,说一说:用小棒表示11(1捆加1根)和用计数器表示11(个位与十位上分别拨1个珠子)有什么相同与不同的地方?
相同点:都用到两种计数单位:“十”与“一”;都有1个十,1个一,是11。
不同点:用小棒表示11时,是用形态不同的1捆和1根小棒来区别“十”与“一”;不论它们放置的位置如何,都表示11。用计数器表示11时,只用形态相同的2颗珠子,是通过珠子的不同位置来区别“十”与“一”的。
讲解:用小棒表示数的方法是十进制的计数方法,用计数器表示数的方法是十进位值制的计数方法。“10个一是1个十”是十进制计数方法的主要特征;珠子或数字处在不同的位置表示不同的数值是位值制计数方法的主要特征。
活动3:初步了解十进制的“满十进1”的计数法则与位值制的计数方法。
(1)请学生分别用小棒、计数器和数字三种方法表示19。通过交流,明确:
① 摆1捆小棒加9根小棒,即“1个十,9个1,是19”。
②在计数器的十位上拨1颗珠子,个位上拨9颗珠子,是19。
③把计数器上表示的数抽象化,就是数的书写形式——数字19。
(2)请学生继续用上述三种方法表示比“19多1”的数。
通过展示交流,理解20是19的后继数。
①以小棒表示的19为基础,再添人1根小棒;把分散的10根小棒捆成1捆;说明“比19多l”的数是“2个十,是20”。
②以计数器表示的19为基础,在个位上再加1颗珠子,个位上的10颗珠子表示10个 “一”,相当于十位上的1颗珠子表示的1个十。所以,可以在十位上添上1颗珠子,取代个位上的10颗珠子。这时,十位上有2颗珠子,个位上没有珠子,即“2个十,是20”。
告诉学生,当较小的计数单位(“个”)累计到10个时,就用1个较大的计数单位(“十”)取而代之,是十进制计数法的计数法则,这个法则可以简称为“满十进1”。
四、课堂练习
教科书第75页第1,2题;第76页第5,6,8题。(可以直接写在书上。)
第2题的要求是在计数器的档上画出珠子,直观表示给出的数。
第8题要在看懂淘气和笑笑怎么分析18这个数的基础上,换一个数(如15)再分析它。
如果时间允许,可以让小组讨论第1题看图写数:哪些图是十进制计数方法?哪些是十进位值制计数方法?(除计数器表示数是十进位值制的计数方法外,其余都只是十进制的计数方法)
五、课堂小结
先让学生说一说,这节课给自己留下最深的印象是什么?
教师可小结:今天我们对数的认识,从10以内拓展到20以内,认识的数多了10个,但表示数的符号还是10个,没有增加。这是为什么呢?因为同一个数字在不同的数位上表示不同的数值,所以,用较少的数字符号可以表示很多的数,位值制的智慧与优越性就在这里。
第2课时教学设计
一、学习目标
在实现第1课时三个学习目标的基础上,再达成如下一个学习目标:
认识20以内数的有序性,探索并掌握20以内数比较大小的方法。
二、过程预设
活动1:读标有O~20的刻度尺。
每个人自由地读尺子上的数。先从O读到10,稍停,继续读到20,再从20倒着读到10。
思考以下问题。
(1)从O读到10与从10继续读到20,你有什么感受或发现?
从0~10与从10~20都包含11个数。不仅从数的书写形式上有规律(后者比前者在十位上多个1),而且从听觉上也有一种周而复始的重复感。
(2)从10读到20,与从20读到10,两者有什么区别?
读数的顺序不同。从10读到20是顺着读,越读越大;从20读到10是倒着读,越读越小。
活动2:比一比12与14,谁大?谁小?
独立思考,解决上述比较大小的问题,再展示交流。
方法1:从12开始,要顺着数才能数到14,所以14比12大。
方法2:12的直观形式——1捆小棒加2根小棒;14的直观形式——1捆小棒加4根小棒。4根小棒比2根多,所以14比12大。
方法3:12=10+2,14=10+4,因为4>2,所以14>12。
讲解:方法1和方法3的共同特征是能够摆脱数的直观形式,直接用抽象的数字进行思考,所以思维水平都比较高。方法2是方法3的直观背景,方法3是方法2的符号表达;方法3是在分析数的结构的基础上,由已知推出未知。
本题还有如下的一种由已知推出未知的方法:
方法4:14>13,13>12,所以,14>12。其直观背景是:14根小棒比13根多,13根比12根多,所以14根小棒比12根多。
对于一年级小学生,方法3或方法4只要求能够结合直观背景加以理解即可。但教师应该知道方法3与方法4的数学背景:方法3是根据不等式的基本性质(不等式的加法单调性),方法4则是根据大于关系的传递性。
活动3:模仿古人用石子或算筹(小棒)表示12的方式表示13。
独立思考并解答,教师反馈正确答案。
反思:用摆石子的方式表示数与用算筹表示数,有什么区别?
讲解:用石子表示数是十进制的计数方法,它所表示的数与大石子或小石子的位置无关;用算筹表示数是十进位值制的计数方法,用算筹表示数还有个规定:个位上的数摆成纵式,十位上的数摆成横式,纵横交错。十进制的计数方法与十进位值制的计数方法,两者明显的区别是,十进制的计数方法需要用不同特征(如捆或根、大或小)的事物表示“十”或“一”等计数单位;而十进位值制的计数方法,只要用相同的事物(如珠子或算筹)摆在不同的位置来表示不同的计数单位。
三、课堂练习
教科书第76页第3,4,7,9题。
第4题,比较11与7的大小,也可以由已知推出未知:11>10,10>7,所以11>7。
四、课堂小结
本课的重点是通过探索20以内数比较大小的方法,认识20以内数的有序性,并能比较20以内数的大小。通过学习“古人计数”,掌握用小棒或计数器等计数工具表示数的方法。用直观形式表示数,目的是把抽象的数变成可以触摸、可操作的思维对象,为进一步学习数的加减法的直观运算打基础。
实施要求
1.每一个数学活动的教学设计,都包括两个基本要素:①要学生做什么?②要学生想什么?对做的事情的思考,即反思。教学设计不是为了灌输,而是为了导出;教师要在组织、引导学生的探索中去倾听学生自己的解释。课堂教学是否精彩,要看学生有没有产生自己的思想和体验。
2.要明确每一个数学活动的思维对象,即通过数学活动要揭示(发现、掌握)的新的、未知的东西是什么。有些新的、未知的东西,学生自己能够发现,如通过数数可以知道牧羊人一共有多少只羊,也可能知道表示“十一”的数字是11,但学生不可能发现新的计数单位“十”,也不可能发明十进位值制计数法。所以,对于学生不可能独立探究的学习内容,必须依靠有意义的接受式学习。教师必须通过讲解帮助学生理解和掌握新的知识,防止为探究而探究,杜绝没有意义、浪费时间的假探究。
3.遵循学生学习数学的心理规律进行教学。夸美纽斯认为,教一个活动最好的方法是演示。维果茨基认为,在最近发展区的框架内,模仿也具有建构的意义。第1课时活动2的第一个环节(学习计数单位“十”)就包括教师的演示和学生的模仿。弗赖登塔尔认为,学一个活动最好的方法是做。第1课时活动2的第二个环节就是让学生相对独立地做数学,引导学生做的过程,是以布鲁纳的儿童认知发展的理论为根据的:从动作认知,到图形认知,再到符号认知。
4.课堂练习是每堂课学生相对独立的学习阶段,教师要放手让学生独立思考,独立作业。只有经过相对独立学习的发展过程,才可能达到完全独立掌握知识的目的,这是一条规律。在练习前,教师有责任帮助学生理解问题,明确练习的要求(如说明第2题“做一做”是做什么,第8题“说一说”要说什么)。在学生练习的过程中,教师不要随意打断学生的思维,要积极巡视,进行个别指导和帮助,并了解练习中比较普遍存在的问题、错误、困难和差异,以便课后反思,并在下一节课进行更有针对性的教学。
