20.4 课题学习 最短路径问题同步课时作业
文档属性
| 名称 | 20.4 课题学习 最短路径问题同步课时作业 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-03 00:00:00 | ||
图片预览



文档简介
20.4 课题学习 最短路径问题同步课时作业
姓名:___________班级:___________考号:___________
一、选择题
1.如图,MN是等边三角形ABC的一条对称轴,D为AC的中点,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD的度数是( )
A. 30° B. 15° C. 20° D. 35°
2.如图,∠AOB=30°,点P为∠AOB内一点,OP=10,点M、N分别在OA、OB上,求△PMN周长的最小值( )
A. 5 B. 10 C. 15 D. 20
3.如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,是AD上的动点,是AC边上的动点,则的最小值是( ).
A. 6 B. 4 C. D. 不存在最小值
4.如图所示,Rt△ABC中,∠ ACB =90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E、F分别是AD、AC上的动点,使CE+EF的和最小,则这个最小值为( )
A. B. C. 3 D. 6
6.如图,在中, ,面积是, 的垂直平分线分别交、边于、点,若点为边的中点,点为线段上一动点,则周长的最小值为( ).
A. B. C. D.
7.如图,在等腰△ABC中,AB=AC=6,∠ACB=75°,AD⊥BC于D,点M、N分别是线段AB、AD上的动点,则MN+BN的最小值是( )
A. 3 B. C. 4.5 D. 6
二、填空题
8.如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,△PMN的周长最小值为________.
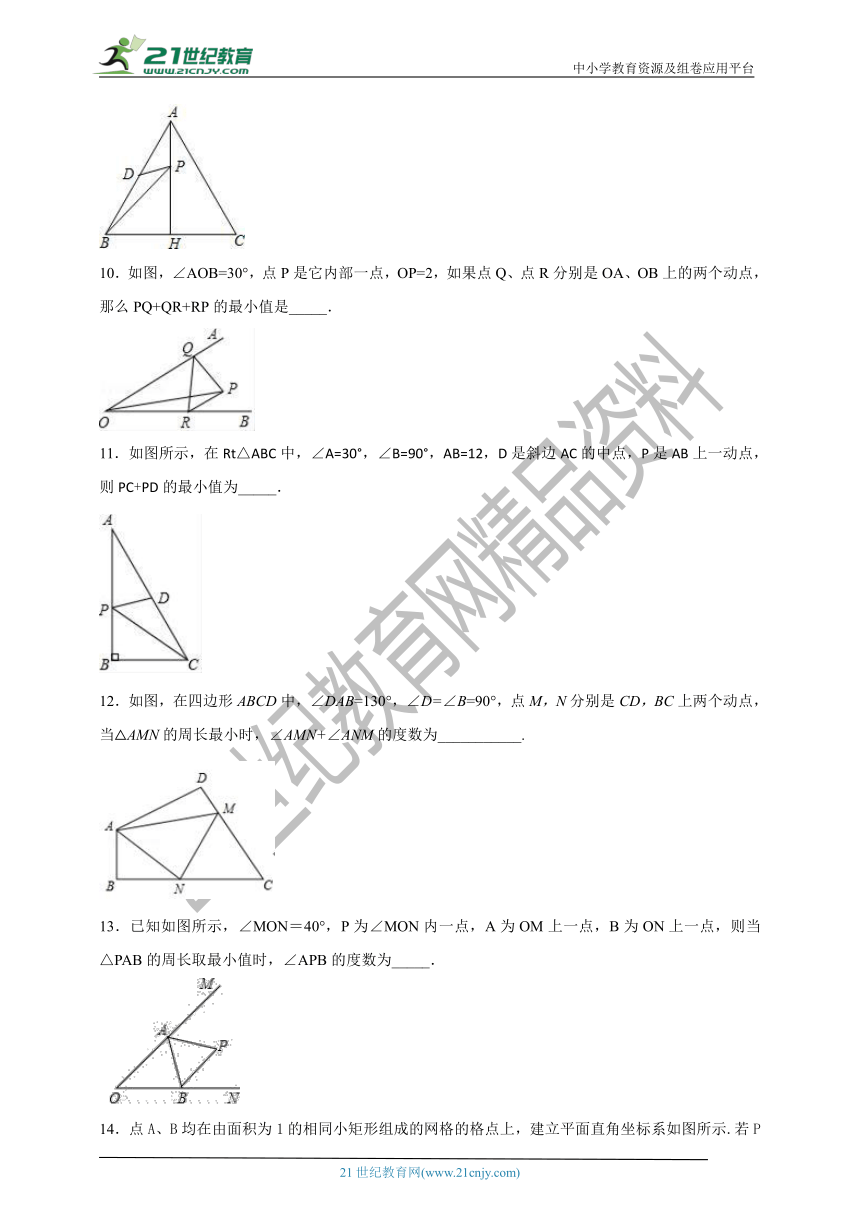
9.如图,在等边△ABC中,AH⊥BC,垂足为H,且AH=6cm,点D是AB的中点,点P是AH上一动点,则DP与BP和的最小值是______cm.
10.如图,∠AOB=30°,点P是它内部一点,OP=2,如果点Q、点R分别是OA、OB上的两个动点,那么PQ+QR+RP的最小值是_____.
11.如图所示,在Rt△ABC中,∠A=30°,∠B=90°,AB=12,D是斜边AC的中点,P是AB上一动点,则PC+PD的最小值为_____.
12.如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为___________.
13.已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为_____.
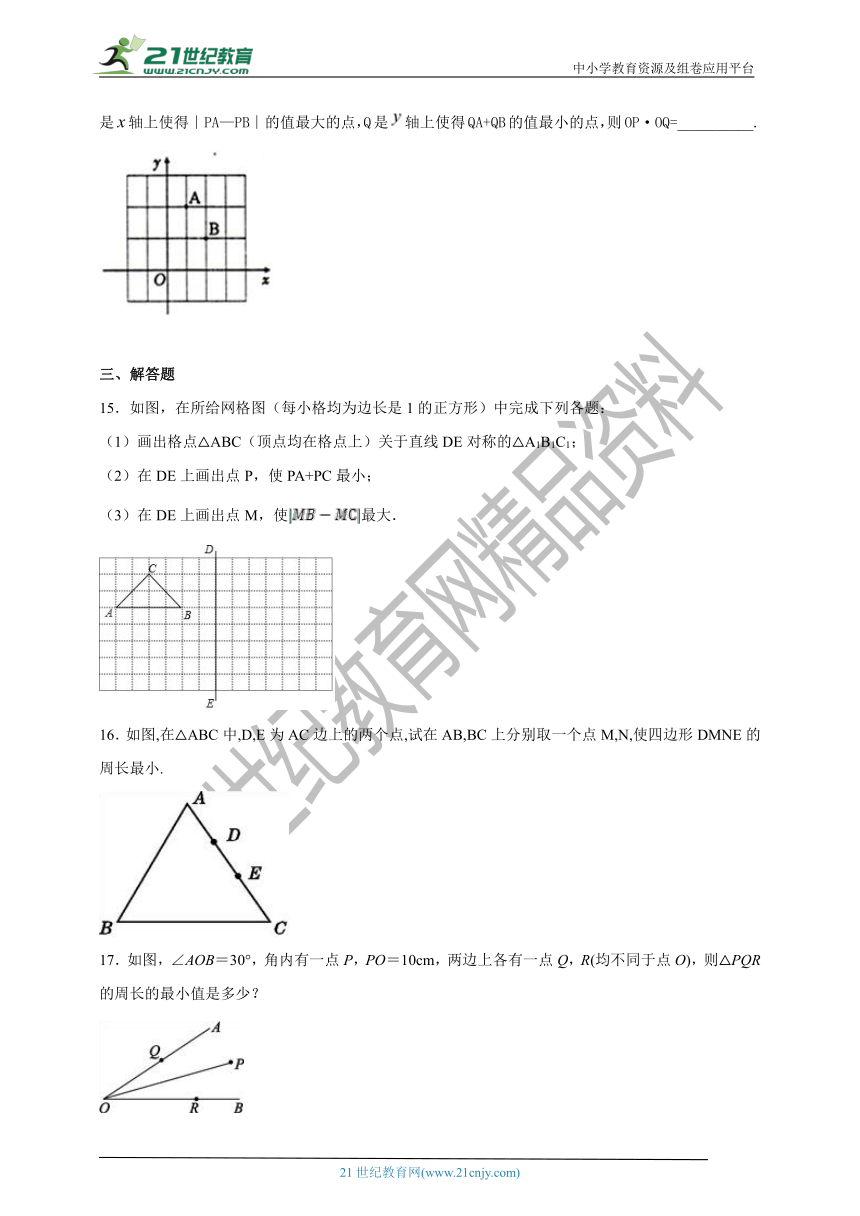
14.点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是轴上使得∣PA—PB∣的值最大的点,Q是轴上使得QA+QB的值最小的点,则OP·OQ=__________.
三、解答题
15.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PA+PC最小;
(3)在DE上画出点M,使最大.
16.如图,在△ABC中,D,E为AC边上的两个点,试在AB,BC上分别取一个点M,N,使四边形DMNE的周长最小.
17.如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长的最小值是多少?
18.最短路径问题:
例:如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.
解:只有A、C、B在一直线上时,才能使AC+BC最小.作点A关于直线“街道”的对称点A′,然后连接A′B,交“街道”于点C,则点C就是所求的点.
应用:已知:如图A是锐角∠MON内部任意一点,
在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.
(1)借助直角三角板在下图中找出符合条件的点B和C.
(2)若∠MON=30°,OA=10,求三角形的最小周长。
19.(1)如图,点A、B、C在直线l的同侧,在直线l上,求作一点P,使得四边形APBC的周长最小;
(2)如图,已知线段a,点A、B在直线l的同侧,在直线l上,求作两点P、Q (点P在点Q的左侧)且PQ=a,四边形APQB的周长最小.
20.已知:A、B两点在直线l的同侧,试分别画出符合条件的点M.
(1)如图,在l上求作一点M,使得| AM-BM |最小;
作法:
(2)如图,在l上求作一点M,使得|AM-BM|最大;
作法:
(3)如图,在l上求作一点M,使得AM+BM最小.
参考答案
1.A
【解析】分析:由于点C关于直线MN的对称点是B,所以当三点在同一直线上时,的值最小.
详解:由题意知,当B.?P、D三点位于同一直线时,PC+PD取最小值,
连接BD交MN于P,
∵△ABC是等边三角形,D为AC的中点,
∴BD⊥AC,
∴PA=PC,
∴
点睛:考查轴对称-最短路线问题,找出点C关于直线MN的对称点是B,根据两点之间,线段最短求解即可.
2.B
【解析】试题解析:分别作点P关于OA、OB的对称点,连,交于,交于,
则
则的周长的最小值为.
∴△OP1P2是等边三角形.
的周长
故选B
3.C
【解析】分析:
由已知条件可知,点B和点C关于AD对称,由此可知,CF+EF=BF+EF,因此当点B、E、F三点在同一直线上,且BE⊥AC时,CF+EF的值最小,计算出此时BE的长度即可.
详解:
如下图,过点B作BE⊥AC于点E,交AD于点F,
∵AB=AC=5,AD是BC边上的中线,
∴AD⊥BC于点D,
∴点B和点C关于AD对称,
∴CF+EF=BF+EF,
∴当点B、E、F三点在同一直线上,且BE⊥AC时,CF+EF的值最小,
∵BE⊥AC于点E,AD⊥BC于点D,
∴S△ABC=AC·BE=AD·BC,即,
解得:BE=,
∴CF+EF的最小值为:.
故选C.
点睛:“能由已知条件分析得到当BE⊥AC于点E时,CF+EF的值最小”是解答本题的关键.
4.B
【解析】分析:过点C作CM⊥AB,从而得出CM的长度就是CE+EF的最小值,根据直角三角形斜边上的高线得出答案.
详解:过点C作CM⊥AB,则CE+EF的最小值就是线段CM的长度,
∵AC=6,BC=8, ∴AB=10,则CM=,故选B.
点睛:本题主要考查的就是三角形中求最值的问题,属于中等难度题型.解决这种问题的关键就是做对称,从而得出答案.
6.D
【解析】连接交于点,此时周长最小,
∵, 为中点,
∴,
∵, ,
∴,
则周长,
∵垂直平分,
∴,
又, 为中点,
∴,
∴周长,
故选D.
【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.
7.A
【解析】解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.∵AB=AC,AD⊥BC于D,∴∠ABC=∠C,AD是∠BAC的平分线,∴M′H=M′N′,∴BH是点B到直线AC的最短距离(垂线段最短),∵∠ABC=∠C,∠ACB=75°,∴∠BAC=30°,∵BH⊥AC,∴BH=AB=3.故选A.
点睛:本题考查的是轴对称﹣最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过三线合一的性质,垂线段最短,确定线段和的最小值.
8.6
【解析】
作P点关于射线OA的对称点C点,作P点关于射线OB的对称点D点,连接CD,CD与射线OA、OB的交点即为M点、N点,连接PM、PN,此时△PMN的周长最小,
∵C点、P点关于射线OA对称,
∴射线OA垂直平分PC,
∴CO=OP=6,CM=PM,
∴∠COA=∠AOP,
同理可证:∠POB=∠DOB,PN=ND,PO=OD=6,
∴CO=OD,
∵∠AOB=∠AOP+∠BOP=30°,
∴∠COD=2∠AOP+2∠BOP=2(∠AOP+∠BOP)=60°,
∴△COD是等边三角形,
∴CD=6,
∴C△PMN=PM+PN+MN=MC+ND+MN=CD=6.
故答案为6.
点睛:本题首先根据△PMN周长最小确定M点、N点的位置,再根据轴对称的性质、等边三角形的判定及性质将△PMN的周长转化为线段的长度.
9.6
【解析】
【分析】
作点B关于AH的对称点B′,由等边三角形的性质可知B′与点C重合,连接CD,则CD的长度即为DP与BP和的最小值,由等边三角形的性质可求出△CAD≌△ACH,则CD=AH=6cm.
【详解】
作点B关于AH的对称点B′, ∵△ABC是等边三角形, ∴B′与点C重合,连接CD,则CD的长度即为DP与BP和的最小值, ∵△ABC是等边三角形,D为AB的中点, ∴CD⊥AB,∠ACD=30°, ∵AH⊥BC, ∴∠CAH=30°,AC=AC, ∴△CAD≌△ACH, ∴CD=AH=6cm.
故答案为:6
【点睛】
本题考查的是最短线路问题及等边三角形的性质,熟知两点之间线段最短的知识是解答此题的关键.
10.2.
【解析】
【分析】
先作点P关于OA,OB的对称点P′,P″,连接P′P″,由轴对称确定最短路线问题,P′P″分别与OA,OB的交点即为Q,R,△PQR周长的最小值=P′P″,由轴对称的性质,可证∠POA=∠P′OA,∠POB=∠P″OB,OP′=OP″=OP=2, ∠P′OP″=2∠AOB=2×30°=60°,继而可得△OP′P″是等边三角形,即PP′=OP′=2.
【详解】
作点P关于OA,OB的对称点P′,P″,连接P′P″,
由轴对称确定最短路线问题,P′P″分别与OA,OB的交点即为Q,R,
△PQR周长的最小值=P′P″,由轴对称的性质,
∠POA=∠P′OA,∠POB=∠P″OB,OP′=OP″=OP=2,
所以,∠P′OP″=2∠AOB=2×30°=60°,
所以,△OP′P″是等边三角形,
所以,PP′=OP′=2.
故答案为:2.
【点睛】
本题主要考查轴对称和等边三角形的判定,解决本题的关键是要熟练掌握轴对称性质和等边三角形的判定.
11.12
【解析】
【分析】
作C关于AB的对称点E,连接ED,易求∠ACE=60°,则AC=AE,且△ACE为等边三角形,CP+PD=DP+PE为E与直线AC之间的连接线段,其最小值为E到AC的距离=AB=12,所以最小值为12.
【详解】
作C关于AB的对称点E,连接ED,
∵∠B=90°,∠A=30°,
∴∠ACB=60°,
∵AC=AE,
∴△ACE为等边三角形,
∴CP+PD=DP+PE为E与直线AC之间的连接线段,
∴最小值为C'到AC的距离=AB=12,
故答案为:12
【点睛】
本题考查的是最短线路问题及等边三角形的性质,熟知两点之间线段最短的知识是解答此题的关键.
12.100°
【解析】解:如图,作点A关于BC的对称点A′,关于CD的对称点A″,
连接A′A″与BC、CD的交点即为所求的点M、N,
∵∠BAD=130°,∠B=∠D=90°,
∴∠A′+∠A″=180°-∠130°=50°,
由轴对称的性质得:∠A′=∠A′AM,∠A″=∠A″AN,
∴∠AMN+∠ANM=2(∠A′+∠A″)=2×50°=100°.
故答案为:100°.
点睛:本题考查了轴对称确定最短路线问题,轴对称的性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,确定出点M、N的位置是解题的关键,要注意整体思想的利用.
13.100°
【解析】如图,作出P点关于OM,ON的对称点P1,P2交OM,ON于A,B两点,此时△PAB的周长最小,根据题意可知: ∠P1PP2=180°-∠MON=180°-40°=140,
所以∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,
所以∠APB=140°-40°=100°,因此,本题正确答案为:100°.
14.5
【解析】
连接AB并延长交x轴于点P,由三角形的三边关系可知,点P即为x轴上使得|PA?PB|的值最大的点,
∵点B是2x2的正方形的对角线的交点,
∴点P即为AB延长线上的点,此时P(3,0)即OP=3;
作A点关于y轴的对称点A′连接A′B交y轴于点Q,则A′B即为QA+QB的最小值,
∵A′(?1,2),B(2,1),
设过A′B的直线为:y=kx+b,则,
解得,
∴Q(0, ),即OQ=,
∴OPOQ=3×=5.
故答案为:5.
点睛:本题考查的是轴对称-最短路径问题,根据题意得出P、Q两点的坐标是解答此题的关键。凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
15.作图见解析.
【解析】分析:(1)根据网格结构找出点A、B、C关于直线DE对称点A1、B1、C1的位置,然后顺次连接即可;
(2)连接AC1,与DE的交点就是点P;
(3)延长CB交DE于点M,则M即为所求的点.
详解:作图如下:
点睛:本题主要考查有关轴对称﹣最短路线的问题中的作图步骤,用到的知识点为:两点之间,线段最短.注意作图形变换这类题的关键是找到图形的对应点.
16.见解析
【解析】试题分析:作点D关于直线AB的对称点D',作点E关于直线BC的对称点E'.连接D'E'交AB于点M,交BC于点N.连接DM,EN.四边形DMNE就是符合要求的四边形.
试题解析:
如图,(1)作点D关于直线AB的对称点D',作点E关于直线BC的对称点E'.(2)连接D'E'交AB于点M,交BC于点N.(3)连接DM,EN.
四边形DMNE就是符合要求的四边形,此时周长最小.
点睛:本题主要考查了轴对称最短路线应用以及轴对称的性质,得出M、N点位置是解题关键.
17.10cm
【解析】试题分析:设点P关于OA的对称点是E,关于OB的对称点是F,当点R、Q在EF上时,△PQR的周长=PQ+QR+PR=EF,此时周长最小.
试题解析:作出点P关于OA的对称点E,作出点P关于OB的对称点F,连接EF,交OA于Q,交OB于R.连接PQ,PR,PE,PF,OE,OF,
则PQ=EQ,PR=RF,
则△PQR的周长=PQ+QR+PR=EQ+QR+RF=EF,
∵∠AOP=∠AOE,∠POB=∠FOB,∠AOB=∠AOP+∠POB=30°,
∴∠EOF=90°,
又∵OE=OP,OF=OP,
∴OE=OF=10,
即△EOF是等边三角形,
∴EF=OP=10,
所以△PQR的周长的最小值为10.
18.(1)见解析;(2)10
【解析】试题分析: 作点关于的对称点,关于的对称点,连接,与相交于两点,连接, 即为所求.
试题解析: 作点关于的对称点,关于的对称点,连接,与相交于两点,连接, 即为所求.
此时线段的长度即为周长的最小值
连接
由对称性知:
为等边三角形
所以三角形的最小周长为10.
点睛:属于将军饮马问题,依据是:两点之间,线段最短.
19.答案见解析
【解析】试题分析: 根据两点之间线段最短,作点A关于直线l的对称点A',A'B交l于P点,则四边形的周长最短.
点A'与A关于直线l对称,点B向左平移个单位至B',连接A'B'交l于P点.
试题解析:
点A'与A关于直线l对称,连接A'B交l于P点.如图所示:
(2)点A'与A关于直线l对称,点B向左平移个单位至B',连接A'B'交l于P点.
如图所示:
20.答案见解析
【解析】试题分析:(1)连接,作的垂直平分线交l于M点
(2)作射线交l于M点
(3)点A'与A关于直线l对称,连接A'B交l于M点
试题解析:
(1)连接,作的垂直平分线交l于M点
∵直线是的垂直平分线,
(2)作射线交l于M点,
假设存在点
构成三角形,
满足使得 最大.
(3)点A'与A关于直线l对称,连接A'B交l于M点
姓名:___________班级:___________考号:___________
一、选择题
1.如图,MN是等边三角形ABC的一条对称轴,D为AC的中点,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD的度数是( )
A. 30° B. 15° C. 20° D. 35°
2.如图,∠AOB=30°,点P为∠AOB内一点,OP=10,点M、N分别在OA、OB上,求△PMN周长的最小值( )
A. 5 B. 10 C. 15 D. 20
3.如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,是AD上的动点,是AC边上的动点,则的最小值是( ).
A. 6 B. 4 C. D. 不存在最小值
4.如图所示,Rt△ABC中,∠ ACB =90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E、F分别是AD、AC上的动点,使CE+EF的和最小,则这个最小值为( )
A. B. C. 3 D. 6
6.如图,在中, ,面积是, 的垂直平分线分别交、边于、点,若点为边的中点,点为线段上一动点,则周长的最小值为( ).
A. B. C. D.
7.如图,在等腰△ABC中,AB=AC=6,∠ACB=75°,AD⊥BC于D,点M、N分别是线段AB、AD上的动点,则MN+BN的最小值是( )
A. 3 B. C. 4.5 D. 6
二、填空题
8.如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,△PMN的周长最小值为________.
9.如图,在等边△ABC中,AH⊥BC,垂足为H,且AH=6cm,点D是AB的中点,点P是AH上一动点,则DP与BP和的最小值是______cm.
10.如图,∠AOB=30°,点P是它内部一点,OP=2,如果点Q、点R分别是OA、OB上的两个动点,那么PQ+QR+RP的最小值是_____.
11.如图所示,在Rt△ABC中,∠A=30°,∠B=90°,AB=12,D是斜边AC的中点,P是AB上一动点,则PC+PD的最小值为_____.
12.如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为___________.
13.已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为_____.
14.点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是轴上使得∣PA—PB∣的值最大的点,Q是轴上使得QA+QB的值最小的点,则OP·OQ=__________.
三、解答题
15.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PA+PC最小;
(3)在DE上画出点M,使最大.
16.如图,在△ABC中,D,E为AC边上的两个点,试在AB,BC上分别取一个点M,N,使四边形DMNE的周长最小.
17.如图,∠AOB=30°,角内有一点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长的最小值是多少?
18.最短路径问题:
例:如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.
解:只有A、C、B在一直线上时,才能使AC+BC最小.作点A关于直线“街道”的对称点A′,然后连接A′B,交“街道”于点C,则点C就是所求的点.
应用:已知:如图A是锐角∠MON内部任意一点,
在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.
(1)借助直角三角板在下图中找出符合条件的点B和C.
(2)若∠MON=30°,OA=10,求三角形的最小周长。
19.(1)如图,点A、B、C在直线l的同侧,在直线l上,求作一点P,使得四边形APBC的周长最小;
(2)如图,已知线段a,点A、B在直线l的同侧,在直线l上,求作两点P、Q (点P在点Q的左侧)且PQ=a,四边形APQB的周长最小.
20.已知:A、B两点在直线l的同侧,试分别画出符合条件的点M.
(1)如图,在l上求作一点M,使得| AM-BM |最小;
作法:
(2)如图,在l上求作一点M,使得|AM-BM|最大;
作法:
(3)如图,在l上求作一点M,使得AM+BM最小.
参考答案
1.A
【解析】分析:由于点C关于直线MN的对称点是B,所以当三点在同一直线上时,的值最小.
详解:由题意知,当B.?P、D三点位于同一直线时,PC+PD取最小值,
连接BD交MN于P,
∵△ABC是等边三角形,D为AC的中点,
∴BD⊥AC,
∴PA=PC,
∴
点睛:考查轴对称-最短路线问题,找出点C关于直线MN的对称点是B,根据两点之间,线段最短求解即可.
2.B
【解析】试题解析:分别作点P关于OA、OB的对称点,连,交于,交于,
则
则的周长的最小值为.
∴△OP1P2是等边三角形.
的周长
故选B
3.C
【解析】分析:
由已知条件可知,点B和点C关于AD对称,由此可知,CF+EF=BF+EF,因此当点B、E、F三点在同一直线上,且BE⊥AC时,CF+EF的值最小,计算出此时BE的长度即可.
详解:
如下图,过点B作BE⊥AC于点E,交AD于点F,
∵AB=AC=5,AD是BC边上的中线,
∴AD⊥BC于点D,
∴点B和点C关于AD对称,
∴CF+EF=BF+EF,
∴当点B、E、F三点在同一直线上,且BE⊥AC时,CF+EF的值最小,
∵BE⊥AC于点E,AD⊥BC于点D,
∴S△ABC=AC·BE=AD·BC,即,
解得:BE=,
∴CF+EF的最小值为:.
故选C.
点睛:“能由已知条件分析得到当BE⊥AC于点E时,CF+EF的值最小”是解答本题的关键.
4.B
【解析】分析:过点C作CM⊥AB,从而得出CM的长度就是CE+EF的最小值,根据直角三角形斜边上的高线得出答案.
详解:过点C作CM⊥AB,则CE+EF的最小值就是线段CM的长度,
∵AC=6,BC=8, ∴AB=10,则CM=,故选B.
点睛:本题主要考查的就是三角形中求最值的问题,属于中等难度题型.解决这种问题的关键就是做对称,从而得出答案.
6.D
【解析】连接交于点,此时周长最小,
∵, 为中点,
∴,
∵, ,
∴,
则周长,
∵垂直平分,
∴,
又, 为中点,
∴,
∴周长,
故选D.
【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.
7.A
【解析】解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.∵AB=AC,AD⊥BC于D,∴∠ABC=∠C,AD是∠BAC的平分线,∴M′H=M′N′,∴BH是点B到直线AC的最短距离(垂线段最短),∵∠ABC=∠C,∠ACB=75°,∴∠BAC=30°,∵BH⊥AC,∴BH=AB=3.故选A.
点睛:本题考查的是轴对称﹣最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过三线合一的性质,垂线段最短,确定线段和的最小值.
8.6
【解析】
作P点关于射线OA的对称点C点,作P点关于射线OB的对称点D点,连接CD,CD与射线OA、OB的交点即为M点、N点,连接PM、PN,此时△PMN的周长最小,
∵C点、P点关于射线OA对称,
∴射线OA垂直平分PC,
∴CO=OP=6,CM=PM,
∴∠COA=∠AOP,
同理可证:∠POB=∠DOB,PN=ND,PO=OD=6,
∴CO=OD,
∵∠AOB=∠AOP+∠BOP=30°,
∴∠COD=2∠AOP+2∠BOP=2(∠AOP+∠BOP)=60°,
∴△COD是等边三角形,
∴CD=6,
∴C△PMN=PM+PN+MN=MC+ND+MN=CD=6.
故答案为6.
点睛:本题首先根据△PMN周长最小确定M点、N点的位置,再根据轴对称的性质、等边三角形的判定及性质将△PMN的周长转化为线段的长度.
9.6
【解析】
【分析】
作点B关于AH的对称点B′,由等边三角形的性质可知B′与点C重合,连接CD,则CD的长度即为DP与BP和的最小值,由等边三角形的性质可求出△CAD≌△ACH,则CD=AH=6cm.
【详解】
作点B关于AH的对称点B′, ∵△ABC是等边三角形, ∴B′与点C重合,连接CD,则CD的长度即为DP与BP和的最小值, ∵△ABC是等边三角形,D为AB的中点, ∴CD⊥AB,∠ACD=30°, ∵AH⊥BC, ∴∠CAH=30°,AC=AC, ∴△CAD≌△ACH, ∴CD=AH=6cm.
故答案为:6
【点睛】
本题考查的是最短线路问题及等边三角形的性质,熟知两点之间线段最短的知识是解答此题的关键.
10.2.
【解析】
【分析】
先作点P关于OA,OB的对称点P′,P″,连接P′P″,由轴对称确定最短路线问题,P′P″分别与OA,OB的交点即为Q,R,△PQR周长的最小值=P′P″,由轴对称的性质,可证∠POA=∠P′OA,∠POB=∠P″OB,OP′=OP″=OP=2, ∠P′OP″=2∠AOB=2×30°=60°,继而可得△OP′P″是等边三角形,即PP′=OP′=2.
【详解】
作点P关于OA,OB的对称点P′,P″,连接P′P″,
由轴对称确定最短路线问题,P′P″分别与OA,OB的交点即为Q,R,
△PQR周长的最小值=P′P″,由轴对称的性质,
∠POA=∠P′OA,∠POB=∠P″OB,OP′=OP″=OP=2,
所以,∠P′OP″=2∠AOB=2×30°=60°,
所以,△OP′P″是等边三角形,
所以,PP′=OP′=2.
故答案为:2.
【点睛】
本题主要考查轴对称和等边三角形的判定,解决本题的关键是要熟练掌握轴对称性质和等边三角形的判定.
11.12
【解析】
【分析】
作C关于AB的对称点E,连接ED,易求∠ACE=60°,则AC=AE,且△ACE为等边三角形,CP+PD=DP+PE为E与直线AC之间的连接线段,其最小值为E到AC的距离=AB=12,所以最小值为12.
【详解】
作C关于AB的对称点E,连接ED,
∵∠B=90°,∠A=30°,
∴∠ACB=60°,
∵AC=AE,
∴△ACE为等边三角形,
∴CP+PD=DP+PE为E与直线AC之间的连接线段,
∴最小值为C'到AC的距离=AB=12,
故答案为:12
【点睛】
本题考查的是最短线路问题及等边三角形的性质,熟知两点之间线段最短的知识是解答此题的关键.
12.100°
【解析】解:如图,作点A关于BC的对称点A′,关于CD的对称点A″,
连接A′A″与BC、CD的交点即为所求的点M、N,
∵∠BAD=130°,∠B=∠D=90°,
∴∠A′+∠A″=180°-∠130°=50°,
由轴对称的性质得:∠A′=∠A′AM,∠A″=∠A″AN,
∴∠AMN+∠ANM=2(∠A′+∠A″)=2×50°=100°.
故答案为:100°.
点睛:本题考查了轴对称确定最短路线问题,轴对称的性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,确定出点M、N的位置是解题的关键,要注意整体思想的利用.
13.100°
【解析】如图,作出P点关于OM,ON的对称点P1,P2交OM,ON于A,B两点,此时△PAB的周长最小,根据题意可知: ∠P1PP2=180°-∠MON=180°-40°=140,
所以∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,
所以∠APB=140°-40°=100°,因此,本题正确答案为:100°.
14.5
【解析】
连接AB并延长交x轴于点P,由三角形的三边关系可知,点P即为x轴上使得|PA?PB|的值最大的点,
∵点B是2x2的正方形的对角线的交点,
∴点P即为AB延长线上的点,此时P(3,0)即OP=3;
作A点关于y轴的对称点A′连接A′B交y轴于点Q,则A′B即为QA+QB的最小值,
∵A′(?1,2),B(2,1),
设过A′B的直线为:y=kx+b,则,
解得,
∴Q(0, ),即OQ=,
∴OPOQ=3×=5.
故答案为:5.
点睛:本题考查的是轴对称-最短路径问题,根据题意得出P、Q两点的坐标是解答此题的关键。凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
15.作图见解析.
【解析】分析:(1)根据网格结构找出点A、B、C关于直线DE对称点A1、B1、C1的位置,然后顺次连接即可;
(2)连接AC1,与DE的交点就是点P;
(3)延长CB交DE于点M,则M即为所求的点.
详解:作图如下:
点睛:本题主要考查有关轴对称﹣最短路线的问题中的作图步骤,用到的知识点为:两点之间,线段最短.注意作图形变换这类题的关键是找到图形的对应点.
16.见解析
【解析】试题分析:作点D关于直线AB的对称点D',作点E关于直线BC的对称点E'.连接D'E'交AB于点M,交BC于点N.连接DM,EN.四边形DMNE就是符合要求的四边形.
试题解析:
如图,(1)作点D关于直线AB的对称点D',作点E关于直线BC的对称点E'.(2)连接D'E'交AB于点M,交BC于点N.(3)连接DM,EN.
四边形DMNE就是符合要求的四边形,此时周长最小.
点睛:本题主要考查了轴对称最短路线应用以及轴对称的性质,得出M、N点位置是解题关键.
17.10cm
【解析】试题分析:设点P关于OA的对称点是E,关于OB的对称点是F,当点R、Q在EF上时,△PQR的周长=PQ+QR+PR=EF,此时周长最小.
试题解析:作出点P关于OA的对称点E,作出点P关于OB的对称点F,连接EF,交OA于Q,交OB于R.连接PQ,PR,PE,PF,OE,OF,
则PQ=EQ,PR=RF,
则△PQR的周长=PQ+QR+PR=EQ+QR+RF=EF,
∵∠AOP=∠AOE,∠POB=∠FOB,∠AOB=∠AOP+∠POB=30°,
∴∠EOF=90°,
又∵OE=OP,OF=OP,
∴OE=OF=10,
即△EOF是等边三角形,
∴EF=OP=10,
所以△PQR的周长的最小值为10.
18.(1)见解析;(2)10
【解析】试题分析: 作点关于的对称点,关于的对称点,连接,与相交于两点,连接, 即为所求.
试题解析: 作点关于的对称点,关于的对称点,连接,与相交于两点,连接, 即为所求.
此时线段的长度即为周长的最小值
连接
由对称性知:
为等边三角形
所以三角形的最小周长为10.
点睛:属于将军饮马问题,依据是:两点之间,线段最短.
19.答案见解析
【解析】试题分析: 根据两点之间线段最短,作点A关于直线l的对称点A',A'B交l于P点,则四边形的周长最短.
点A'与A关于直线l对称,点B向左平移个单位至B',连接A'B'交l于P点.
试题解析:
点A'与A关于直线l对称,连接A'B交l于P点.如图所示:
(2)点A'与A关于直线l对称,点B向左平移个单位至B',连接A'B'交l于P点.
如图所示:
20.答案见解析
【解析】试题分析:(1)连接,作的垂直平分线交l于M点
(2)作射线交l于M点
(3)点A'与A关于直线l对称,连接A'B交l于M点
试题解析:
(1)连接,作的垂直平分线交l于M点
∵直线是的垂直平分线,
(2)作射线交l于M点,
假设存在点
构成三角形,
满足使得 最大.
(3)点A'与A关于直线l对称,连接A'B交l于M点
