28.2 二次函数与实际问题同步课时作业(1)
文档属性
| 名称 | 28.2 二次函数与实际问题同步课时作业(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
28.2 二次函数与实际问题同步课时作业(1)
姓名:__________班级:__________考号:__________
一、选择题
长方形的周长为24cm,其中一边为x(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=(12﹣x2) C.y=(12﹣x) x D.y=2(12﹣x)
已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
在一幅长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是ycm2,设金色纸边的宽度为xcm2,那么y关于x的函数是()
A. y=(60+2x)(40+2x) B. y=(60+x)(40+x)
C. y=(60+2x)(40+x) D. y=(60+x)(40+2x)
把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )
A.y= -x2+50x B.y=x2-50x C.y= -x2+25x D.y= -2x2+25
向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0)、若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
周长8m的铝合金制成如图所示形状的矩形窗柜,使窗户的透光面积最大,那么这个窗户的最大透光面积是( )m
A. B. C.4 D.
如图,已知△ABC的顶点坐标分别为A(0,2)、B(1,0)、C(2,1),若二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点,则实数b的取值范围是( )
A.b≤﹣2 B.b<﹣2 C.b≥﹣2 D.b>﹣2
如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
A.y= B.y= C.y= D.y=
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A. cm2 B. cm2 C. cm2 D. cm2
二、填空题
正方形边长3,若边长增加x,则面积增加y,y与x的函数关系式为 .
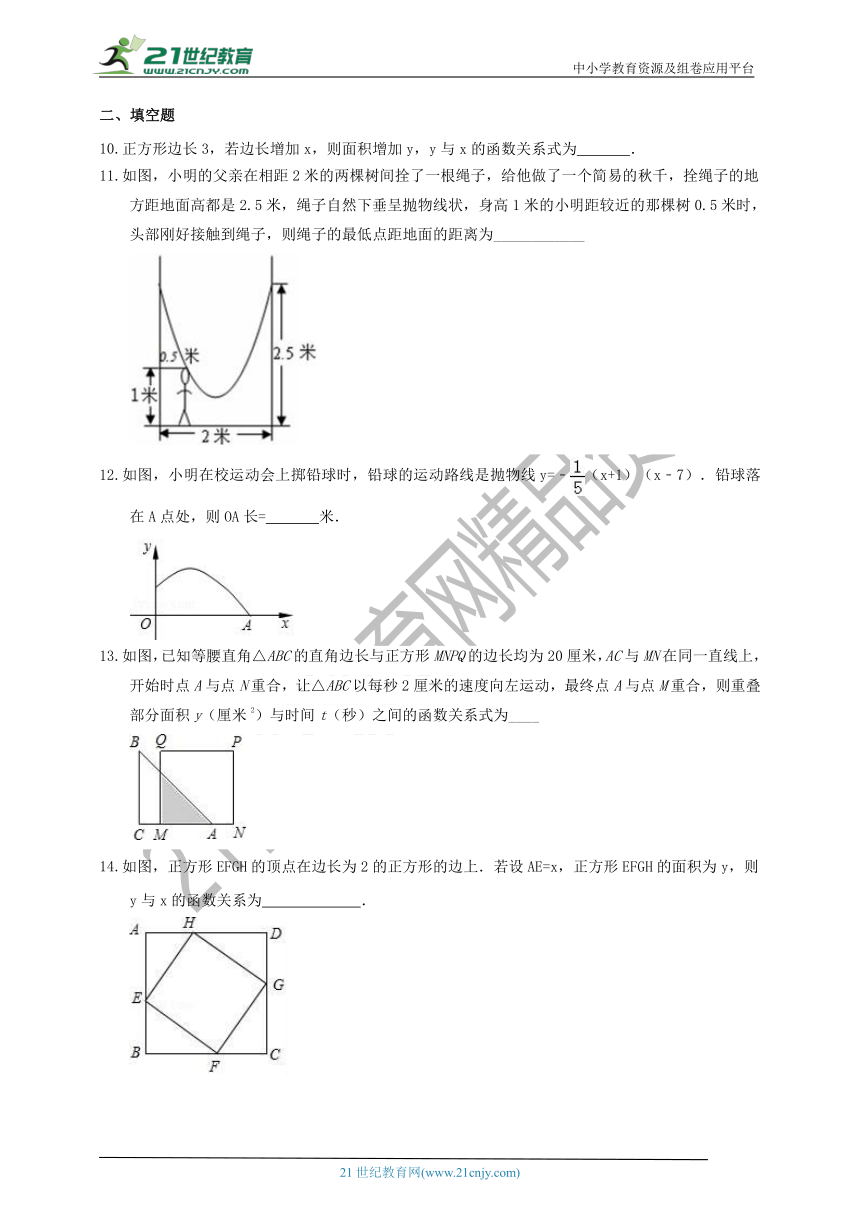
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为____________
如图,小明在校运动会上掷铅球时,铅球的运动路线是抛物线y=﹣(x+1)(x﹣7).铅球落在A点处,则OA长= 米.
如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2厘米的速度向左运动,最终点A与点M重合,则重叠部分面积y(厘米2)与时间t(秒)之间的函数关系式为____
如图,正方形EFGH的顶点在边长为2的正方形的边上.若设AE=x,正方形EFGH的面积为y,则y与x的函数关系为 .
竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过____秒,四边形APQC的面积最小.
三、解答题
已知在△ABC中,∠B=30°,AB+BC=12,设AB=x,△ABC的面积是S,求面积S关于x的函数解析式,并写出自变量x的取值范围.
扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示.
(1)根据图2填表:
x(min) 0 3 6 8 12 …
y(m) …
(2)变量y是x的函数吗?为什么?
(3)根据图中的信息,请写出摩天轮的直径.
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
t(秒) 0 0.16 0.2 0.4 0.6 0.64 0.8 6
X(米) 0 0.4 0.5 1 1.5 1.6 2 …
y(米) 0.25 0.378 0.4 0.45 0.4 0.378 0.25 …
(1)当t为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,y与x满足y=a(x﹣3)2+k.
①用含a的代数式表示k;
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求a的值.
如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
在一块长方形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子.镜子的长与宽的比是2:1.已知镜面玻璃的价格是每平方米120元,边框的价格是每米30元,另外制作这面镜子还需加工费45元.设制作这面镜子的总费用是y元,镜子的宽度是x米.
(1)求y与x之间的关系式.
(2)如果制作这面镜子共花了195元,求这面镜子的长和宽.
已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.
(1)求过A、B、C三点的抛物线的解析式;
(2)若P点是抛物线上的动点,且在第一象限,那么△PAB是否有最大面积?若有,求出此时P点的坐标和△PAB的最大面积;若没有,请说明理由.
答案解析
一 、选择题
【考点】根据实际问题列二次函数关系式.
【分析】先得到长方形的另一边长,那么面积=一边长×另一边长.
解:∵长方形的周长为24cm,其中一边为x(其中x>0),
∴长方形的另一边长为12﹣x,
∴y=(12﹣x) x.
故选C.
点评:考查列二次函数关系式;得到长方形的另一边长是解决本题的易错点.
【考点】二次函数的应用
【分析】分别求出t=9、13、24、10时h的值可判断A、B、C三个选项,将解析式配方成顶点式可判断D选项.
解:A、当t=9时,h=136;当t=13时,h=144;所以点火后9s和点火后13s的升空高度不相同,此选项错误;
B、当t=24时h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、当t=10时h=141m,此选项错误;
D、由h=﹣t2+24t+1=﹣(t﹣12)2+145知火箭升空的最大高度为145m,此选项正确;
故选:D.
【点评】本题主要考查二次函数的应用,解题的关键是熟练掌握二次函数的性质.
考点: 根据实际问题列二次函数关系式.
分析: 挂图的面积=长×宽=(60+2x)(40+2x).
解答: 解:长是:60+2x,宽是:40+2x,
由矩形的面积公式得
则y=(60+2x)(40+2x).
故选A.
点评: 根据题意,找到所求量的等量关系是解决问题的关键.本题需注意长和宽的求法.
【考点】根据实际问题列二次函数关系式
【分析】由长方形的面积=长×宽可求解.
解:设这个长方形的一边长为xcm,则另一边长为(25-x)cm,
所以面积y=x(25-x)= -x2+25x.
故选C.
【考点】二次函数的应用
【分析】此题可归纳为:若抛物线y=ax2+bx+c,当x=a与x=b时y值相等,那么该抛物线的对称轴是直线x=(a+b)/2.
解:由炮弹在第7秒与第14秒时的高度相等,根据抛物线的对称性可知,x=(7+14)/2时,炮弹所在高度最高,所以x=10.5.题中给的四个选项中 B第10秒最接近10.5秒
故选B.
【考点】二次函数的应用
【分析】根据窗户框的形状可设宽为x,其高就是,所以窗户面积S=,再求出二次函数解析式—顶点式即可求出最大面积。
解:设窗户的宽是x,根据题意得
S=
=
∴当窗户宽是m时,面积最大是 m2
【考点】二次函数图象与系数的关系.
【分析】抛物线经过C点时b的值即可.
解:把C(2,1)代入y=x2+bx+1,得
22+2b+1=1,
解得b=﹣2.
故b的取值范围是b≥﹣2.
故选:C.
【考点】根据实际问题列二次函数关系式.
【分析】四边形ABCD图形不规则,根据已知条件,将△ABC绕A点逆时针旋转90°到△ADE的位置,求四边形ABCD的面积问题转化为求梯形ACDE的面积问题;根据全等三角形线段之间的关系,结合勾股定理,把梯形上底DE,下底AC,高DF分别用含x的式子表示,可表示四边形ABCD的面积.
解:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,
∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE
∴∠BAC=∠DAE
又∵AB=AD,∠ACB=∠E=90°
∴△ABC≌△ADE(AAS)
∴BC=DE,AC=AE,
设BC=a,则DE=a,DF=AE=AC=4BC=4a,
CF=AC﹣AF=AC﹣DE=3a,
在Rt△CDF中,由勾股定理得,
CF2+DF2=CD2,即(3a)2+(4a)2=x2,
解得:a=,
∴y=S四边形ABCD=S梯形ACDE=×(DE+AC)×DF
=×(a+4a)×4a
=10a2
=x2.
故选:C.
【点评】本题运用了旋转法,将求不规则四边形面积问题转化为求梯形的面积,充分运用了全等三角形,勾股定理在解题中的作用.
【考点】 二次函数的应用;展开图折叠成几何体;等边三角形的性质..
【分析】 如图,由等边三角形的性质可以得出∠A=∠B=∠C=60°,由三个筝形全等就可以得出AD=BE=BF=CG=CH=AK,根据折叠后是一个三棱柱就可以得出DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO为矩形,且全等.连结AO证明△AOD≌△AOK就可以得出∠OAD=∠OAK=30°,设OD=x,则AO=2x,由勾股定理就可以求出AD=x,由矩形的面积公式就可以表示纸盒的侧面积,由二次函数的性质就可以求出结论.
解:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵筝形ADOK≌筝形BEPF≌筝形AGQH,
∴AD=BE=BF=CG=CH=AK.
∵折叠后是一个三棱柱,
∴DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO都为矩形.
∴∠ADO=∠AKO=90°.
连结AO,
在Rt△AOD和Rt△AOK中,
,
∴Rt△AOD≌Rt△AOK(HL).
∴∠OAD=∠OAK=30°.
设OD=x,则AO=2x,由勾股定理就可以求出AD=x,
∴DE=6﹣2x,
∴纸盒侧面积=3x(6﹣2x)=﹣6x2+18x,
=﹣6(x﹣)2+,
∴当x=时,纸盒侧面积最大为.
故选C.
点评: 本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,矩形的面积公式的运用,二次函数的性质的运用,解答时表示出纸盒的侧面积是关键.
二 、填空题
【考点】根据实际问题列二次函数关系式.
【分析】增加的面积=边长为3+x的新正方形的面积﹣边长为3的正方形的面积,把相关数值代入即可求解.
解:由正方形边长3,边长增加x,增加后的边长为(x+3),
则面积增加y=(x+3)2﹣32=x2+6x+9﹣9=x2+6x.
故应填:y=x2+6x.
【考点】二次函数的应用
【分析】根据题意,运用待定系数法,建立适当的函数解析式,代入求值即可解答.
解:以左边树与地面交点为原点,地面水平线为x轴,左边树为y轴建立平面直角坐标系,由题意可得A(0,2.5),B(2,2.5),C(0.5,1)
设函数解析式为y=ax2+bx+c
把C点代入得出 c=2.5
再把A、B两点分别代入得
解之得a=2,b= -4,
∴y=2x2-4x+2.5=2(x-1)2+0.5.
∵2>0
∴当x=1时,y=0.5米.
∴故答案为:0.5米.
【考点】二次函数的应用.
【分析】当y=0时代入解析式y=﹣(x+1)(x﹣7).求出x的值即可.
解:由题意,得
当y=0时,0=﹣(x+1)(x﹣7),
解得:x1=﹣1(舍去),x2=7.
故答案为:7.
【考点】根据实际问题列二次函数关系
【分析】根据△ABC是等腰直角三角形,则重叠部分也是等腰直角三角形,根据三角形的面积公式即可求解.
解:AM=20-2t,则重叠部分面积y=×AM2= (20-2t)2
【考点】 根据实际问题列二次函数关系式; 正方形的性质.
【分析】由AAS证明△AHE≌△BEF,得出AE=BF=x,AH=BE=2﹣x,再根据勾股定理,求出EH2,即可得到y与x之间的函数关系式.
解:如图所示:
∵四边形ABCD是边长为1的正方形,
∴∠A=∠B=90°,AB=2.
∴∠1+∠2=90°,
∵四边形EFGH为正方形,
∴∠HEF=90°,EH=EF.
∴∠1+∠3=90°,
∴∠2=∠3,
在△AHE与△BEF中,
∵,
∴△AHE≌△BEF(AAS),
∴AE=BF=x,AH=BE=2﹣x,
在Rt△AHE中,由勾股定理得:
EH2=AE2+AH2=x2+(2﹣x)2=2x2﹣4x+4;
即y=2x2﹣4x+4(0<x<2),
故答案为:y=2x2﹣4x+4.
【考点】二次函数的应用.
【分析】设各自抛出后1.1秒时到达相同的最大离地高度为h,这个最大高度为h,则小球的高度y=a(t﹣1.1)2+h,根据题意列出方程即可解决问题.
解:设各自抛出后1.1秒时到达相同的最大离地高度为h,这个最大高度为h,则小球的高度y=a(t﹣1.1)2+h,
由题意a(t﹣1.1)2+h=a(t﹣1﹣1.1)2+h,
解得t=1.6.
故第一个小球抛出后1.6秒时在空中与第二个小球的离地高度相同.
故答案为1.6.
【考点】二次函数的应用
【分析】根据等量关系“四边形APQC的面积=三角形ABC的面积-三角形PBQ的面积”列出函数关系求最小值
解:设P、Q同时出发后经过的时间为t秒,四边形APQC的面积为S平方毫米,
则有:S=S△ABC-S△PBQ
=
=4t2-24t+144
=4(t-3)2+108.
∵4>0
∴当t=3s时,S取得最小值.
三 、解答题
【考点】根据实际问题列二次函数关系式.
【分析】作△ABC的高AD,根据30°角所对的直角边等于斜边的一半得出AD=AB,再根据三角形的面积公式得出△ABC的面积=BC AD,将相关数值代入即可.
解:如图,作△ABC的高AD.
在△ABD中,∵∠ADB=90°,∠B=30°,
∴AD=AB=x,
∴S=△ABC的面积=BC AD=(12﹣x) x=﹣x2+3x,
∴面积S关于x的函数解析式为S=﹣x2+3x(x>0).
点评:本题考查了根据实际问题列二次函数关系式,含30°角的直角三角形的性质,三角形的面积,求出△ABC的高AD是解题的关键.
【考点】二次函数的应用
【分析】设菜园宽为x,则长为30-2x,由面积公式写出y与x的函数关系式,然后利用二次函数的最值的知识可得出菜园的最大面积,及取得最大面积时矩形的长和宽.
解:设矩形的宽为xm,面积为Sm2,根据题意得:
S=x(30-2x)
= -2x2+30x
= -2(x-7.5)2+112.5,
所以当x=7.5时,S最大,最大值为112.5.
30-2x=30-15=15.
【考点】二次函数的应用.
【分析】(1)直接结合图象写出有关点的纵坐标即可;
(2)利用函数的定义直接判断即可.
(3)最高点的纵坐标减去最低点的纵坐标即可求得摩天轮的半径.
解:(1)填表如下:
x(min) 0 3 6 8 12 …
y(m) 5 70 5 54 5 …
(2)因为每给一个x的值有唯一的一个函数值与之对应,符合函数的定义,
所以y是x的函数;
(3)∵最高点为70米,最低点为5米,
∴摩天轮的直径为65米.
【点评】本题考查了二次函数的应用,解题的关键是从实际问题中抽象出函数模型,难度不大.
【考点】二次函数的应用.
【分析】(1)利用网格中数据直接得出乒乓球达到最大高度时的时间;
(2)首先求出函数解析式,进而求出乒乓球落在桌面时,与端点A的水平距离;
(3)①由(2)得乒乓球落在桌面上时,得出对应点坐标,只要利用待定系数法求出函数解析式即可;
②由题意可得,扣杀路线在直线y=x上,由①得,y=a(x﹣3)2﹣a,进而利用根的判别式求出a的值,进而求出x的值.
解:(1)由表格中数据可得,t=0.4(秒),乒乓球达到最大高度;
(2)由表格中数据,可得y是x的二次函数,可设y=a(x﹣1)2+0.45,
将(0,0.25)代入,可得:a=﹣,
则y=﹣(x﹣1)2+0.45,
当y=0时,0=﹣(x﹣1)2+0.45,
解得:x1=,x2=﹣(舍去),
即乒乓球与端点A的水平距离是m;
(3)①由(2)得乒乓球落在桌面上时,对应点为:(,0),
代入y=a(x﹣3)2+k,得(﹣3)2a+k=0,
化简得:k=﹣a;
②由题意可得,扣杀路线在直线y=x上,由①得,y=a(x﹣3)2﹣a,
令a(x﹣3)2﹣a=x,
整理得:20ax2﹣(120a+2)x+175a=0,
当△=(120a+2)2﹣4×20a×175a=0时符合题意,
解方程得:a1=,a2=,
当a1=时,求得x=﹣,不符合题意,舍去;
当a2=时,求得x=,符合题意.
【点评】此题主要考查了二次函数对应用以及根的判别式和一元二次方程的解法等知识,利用图表中数据得出函数解析式是解题关键.
【考点】二次函数的应用.
【分析】(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),于是得到,求得抛物线的解析式为:y=﹣t2+5t+,当t=时,y最大=4.5;
(2)把x=28代入x=10t得t=2.8,当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,于是得到他能将球直接射入球门.
解:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),
∴,
解得:,
∴抛物线的解析式为:y=﹣t2+5t+,
∴当t=时,y最大=4.5;
(2)把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,
∴他能将球直接射入球门.
【点评】本题考查了待定系数法求二次函数的解析式,以及二次函数的应用,正确求得解析式是解题的关键.
【考点】根据实际问题列二次函数关系式;解一元二次方程-因式分解法.
【分析】(1)依题意可得总费用=镜面玻璃费用+边框的费用+加工费用,可得y=6x×30+45+2x2×120化简即可.
(2)根据共花了195元,即玻璃的费用+边框的费用+加工费=195元,即可列出方程求解.
解:(1)y=(2x+2x+x+x)×30+45+2x2×120
=240x2+180x+45;
(2)由题意可列方程为
240x2+180x+45=195,
整理得8x2+6x﹣5=0,即(2x﹣1)(4x+5)=0,
解得x1=0.5,x2=﹣1.25(舍去)
∴x=0.5,
∴2x=1,
答:镜子的长和宽分别是1m和0.5m.
点评:本题是一道一元二次方程的应用题,解这类题关键是理解题意,建立恰当的关系式予以求解.
【考点】二次函数的应用
【分析】(1)求得直线y=3x+3与坐标轴的两交点坐标,然后根据OB=OA即可求得点B的坐标,然后利用待定系数法求得经过A、B、C三点的抛物线的解析式即可;
(2)本问关键是求出△ABP的面积表达式.这个表达式是一个关于P点横坐标的二次函数,利用二次函数求极值的方法可以确定P点的坐标.
解:(1)令y=0得:3x+3=0,x= -1,
故点C的坐标为(-1,0);
令x=0得:y=3x+3=3×0+3=3
故点A的坐标为(0,3);
∵△OAB是等腰直角三角形.
∴ OB=OA=3,
∴点B的坐标为(3,0),
设过A、B、C三点的抛物线的解析式y=ax2+bx+c,
解得:
∴解析式为:y= -x2+2x+3;
(2)存在.如图1所示,设P(x,y)是第一象限的抛物线上一点,
过点P作PN⊥x轴于点N,则ON=x,PN=y,BN=OB-ON=3-x.
S△ABP=S梯形PNOA+S△PNB-S△AOB
=(OA+PN)ON+PNBN - OA×OB
=
=
∵P(x,y)在抛物线上,∴y= -x2+2x+3,代入上式得:
S△ABP== (x2-3x)=
∴当x= 时,S△ABP取得最大值.
当x=时,y= -x2+2x+3= ,
∴P( ).
所以,在第一象限的抛物线上,存在一点P,使得△ABP的面积最大;
P点的坐标为()
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
28.2 二次函数与实际问题同步课时作业(1)
姓名:__________班级:__________考号:__________
一、选择题
长方形的周长为24cm,其中一边为x(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=(12﹣x2) C.y=(12﹣x) x D.y=2(12﹣x)
已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
在一幅长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是ycm2,设金色纸边的宽度为xcm2,那么y关于x的函数是()
A. y=(60+2x)(40+2x) B. y=(60+x)(40+x)
C. y=(60+2x)(40+x) D. y=(60+x)(40+2x)
把一根长为50cm的铁丝弯成一个长方形,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )
A.y= -x2+50x B.y=x2-50x C.y= -x2+25x D.y= -2x2+25
向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0)、若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
周长8m的铝合金制成如图所示形状的矩形窗柜,使窗户的透光面积最大,那么这个窗户的最大透光面积是( )m
A. B. C.4 D.
如图,已知△ABC的顶点坐标分别为A(0,2)、B(1,0)、C(2,1),若二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点,则实数b的取值范围是( )
A.b≤﹣2 B.b<﹣2 C.b≥﹣2 D.b>﹣2
如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
A.y= B.y= C.y= D.y=
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A. cm2 B. cm2 C. cm2 D. cm2
二、填空题
正方形边长3,若边长增加x,则面积增加y,y与x的函数关系式为 .
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为____________
如图,小明在校运动会上掷铅球时,铅球的运动路线是抛物线y=﹣(x+1)(x﹣7).铅球落在A点处,则OA长= 米.
如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20厘米,AC与MN在同一直线上,开始时点A与点N重合,让△ABC以每秒2厘米的速度向左运动,最终点A与点M重合,则重叠部分面积y(厘米2)与时间t(秒)之间的函数关系式为____
如图,正方形EFGH的顶点在边长为2的正方形的边上.若设AE=x,正方形EFGH的面积为y,则y与x的函数关系为 .
竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过____秒,四边形APQC的面积最小.
三、解答题
已知在△ABC中,∠B=30°,AB+BC=12,设AB=x,△ABC的面积是S,求面积S关于x的函数解析式,并写出自变量x的取值范围.
扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示.
(1)根据图2填表:
x(min) 0 3 6 8 12 …
y(m) …
(2)变量y是x的函数吗?为什么?
(3)根据图中的信息,请写出摩天轮的直径.
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
t(秒) 0 0.16 0.2 0.4 0.6 0.64 0.8 6
X(米) 0 0.4 0.5 1 1.5 1.6 2 …
y(米) 0.25 0.378 0.4 0.45 0.4 0.378 0.25 …
(1)当t为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,y与x满足y=a(x﹣3)2+k.
①用含a的代数式表示k;
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求a的值.
如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
在一块长方形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子.镜子的长与宽的比是2:1.已知镜面玻璃的价格是每平方米120元,边框的价格是每米30元,另外制作这面镜子还需加工费45元.设制作这面镜子的总费用是y元,镜子的宽度是x米.
(1)求y与x之间的关系式.
(2)如果制作这面镜子共花了195元,求这面镜子的长和宽.
已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.
(1)求过A、B、C三点的抛物线的解析式;
(2)若P点是抛物线上的动点,且在第一象限,那么△PAB是否有最大面积?若有,求出此时P点的坐标和△PAB的最大面积;若没有,请说明理由.
答案解析
一 、选择题
【考点】根据实际问题列二次函数关系式.
【分析】先得到长方形的另一边长,那么面积=一边长×另一边长.
解:∵长方形的周长为24cm,其中一边为x(其中x>0),
∴长方形的另一边长为12﹣x,
∴y=(12﹣x) x.
故选C.
点评:考查列二次函数关系式;得到长方形的另一边长是解决本题的易错点.
【考点】二次函数的应用
【分析】分别求出t=9、13、24、10时h的值可判断A、B、C三个选项,将解析式配方成顶点式可判断D选项.
解:A、当t=9时,h=136;当t=13时,h=144;所以点火后9s和点火后13s的升空高度不相同,此选项错误;
B、当t=24时h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、当t=10时h=141m,此选项错误;
D、由h=﹣t2+24t+1=﹣(t﹣12)2+145知火箭升空的最大高度为145m,此选项正确;
故选:D.
【点评】本题主要考查二次函数的应用,解题的关键是熟练掌握二次函数的性质.
考点: 根据实际问题列二次函数关系式.
分析: 挂图的面积=长×宽=(60+2x)(40+2x).
解答: 解:长是:60+2x,宽是:40+2x,
由矩形的面积公式得
则y=(60+2x)(40+2x).
故选A.
点评: 根据题意,找到所求量的等量关系是解决问题的关键.本题需注意长和宽的求法.
【考点】根据实际问题列二次函数关系式
【分析】由长方形的面积=长×宽可求解.
解:设这个长方形的一边长为xcm,则另一边长为(25-x)cm,
所以面积y=x(25-x)= -x2+25x.
故选C.
【考点】二次函数的应用
【分析】此题可归纳为:若抛物线y=ax2+bx+c,当x=a与x=b时y值相等,那么该抛物线的对称轴是直线x=(a+b)/2.
解:由炮弹在第7秒与第14秒时的高度相等,根据抛物线的对称性可知,x=(7+14)/2时,炮弹所在高度最高,所以x=10.5.题中给的四个选项中 B第10秒最接近10.5秒
故选B.
【考点】二次函数的应用
【分析】根据窗户框的形状可设宽为x,其高就是,所以窗户面积S=,再求出二次函数解析式—顶点式即可求出最大面积。
解:设窗户的宽是x,根据题意得
S=
=
∴当窗户宽是m时,面积最大是 m2
【考点】二次函数图象与系数的关系.
【分析】抛物线经过C点时b的值即可.
解:把C(2,1)代入y=x2+bx+1,得
22+2b+1=1,
解得b=﹣2.
故b的取值范围是b≥﹣2.
故选:C.
【考点】根据实际问题列二次函数关系式.
【分析】四边形ABCD图形不规则,根据已知条件,将△ABC绕A点逆时针旋转90°到△ADE的位置,求四边形ABCD的面积问题转化为求梯形ACDE的面积问题;根据全等三角形线段之间的关系,结合勾股定理,把梯形上底DE,下底AC,高DF分别用含x的式子表示,可表示四边形ABCD的面积.
解:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,
∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE
∴∠BAC=∠DAE
又∵AB=AD,∠ACB=∠E=90°
∴△ABC≌△ADE(AAS)
∴BC=DE,AC=AE,
设BC=a,则DE=a,DF=AE=AC=4BC=4a,
CF=AC﹣AF=AC﹣DE=3a,
在Rt△CDF中,由勾股定理得,
CF2+DF2=CD2,即(3a)2+(4a)2=x2,
解得:a=,
∴y=S四边形ABCD=S梯形ACDE=×(DE+AC)×DF
=×(a+4a)×4a
=10a2
=x2.
故选:C.
【点评】本题运用了旋转法,将求不规则四边形面积问题转化为求梯形的面积,充分运用了全等三角形,勾股定理在解题中的作用.
【考点】 二次函数的应用;展开图折叠成几何体;等边三角形的性质..
【分析】 如图,由等边三角形的性质可以得出∠A=∠B=∠C=60°,由三个筝形全等就可以得出AD=BE=BF=CG=CH=AK,根据折叠后是一个三棱柱就可以得出DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO为矩形,且全等.连结AO证明△AOD≌△AOK就可以得出∠OAD=∠OAK=30°,设OD=x,则AO=2x,由勾股定理就可以求出AD=x,由矩形的面积公式就可以表示纸盒的侧面积,由二次函数的性质就可以求出结论.
解:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵筝形ADOK≌筝形BEPF≌筝形AGQH,
∴AD=BE=BF=CG=CH=AK.
∵折叠后是一个三棱柱,
∴DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO都为矩形.
∴∠ADO=∠AKO=90°.
连结AO,
在Rt△AOD和Rt△AOK中,
,
∴Rt△AOD≌Rt△AOK(HL).
∴∠OAD=∠OAK=30°.
设OD=x,则AO=2x,由勾股定理就可以求出AD=x,
∴DE=6﹣2x,
∴纸盒侧面积=3x(6﹣2x)=﹣6x2+18x,
=﹣6(x﹣)2+,
∴当x=时,纸盒侧面积最大为.
故选C.
点评: 本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,矩形的面积公式的运用,二次函数的性质的运用,解答时表示出纸盒的侧面积是关键.
二 、填空题
【考点】根据实际问题列二次函数关系式.
【分析】增加的面积=边长为3+x的新正方形的面积﹣边长为3的正方形的面积,把相关数值代入即可求解.
解:由正方形边长3,边长增加x,增加后的边长为(x+3),
则面积增加y=(x+3)2﹣32=x2+6x+9﹣9=x2+6x.
故应填:y=x2+6x.
【考点】二次函数的应用
【分析】根据题意,运用待定系数法,建立适当的函数解析式,代入求值即可解答.
解:以左边树与地面交点为原点,地面水平线为x轴,左边树为y轴建立平面直角坐标系,由题意可得A(0,2.5),B(2,2.5),C(0.5,1)
设函数解析式为y=ax2+bx+c
把C点代入得出 c=2.5
再把A、B两点分别代入得
解之得a=2,b= -4,
∴y=2x2-4x+2.5=2(x-1)2+0.5.
∵2>0
∴当x=1时,y=0.5米.
∴故答案为:0.5米.
【考点】二次函数的应用.
【分析】当y=0时代入解析式y=﹣(x+1)(x﹣7).求出x的值即可.
解:由题意,得
当y=0时,0=﹣(x+1)(x﹣7),
解得:x1=﹣1(舍去),x2=7.
故答案为:7.
【考点】根据实际问题列二次函数关系
【分析】根据△ABC是等腰直角三角形,则重叠部分也是等腰直角三角形,根据三角形的面积公式即可求解.
解:AM=20-2t,则重叠部分面积y=×AM2= (20-2t)2
【考点】 根据实际问题列二次函数关系式; 正方形的性质.
【分析】由AAS证明△AHE≌△BEF,得出AE=BF=x,AH=BE=2﹣x,再根据勾股定理,求出EH2,即可得到y与x之间的函数关系式.
解:如图所示:
∵四边形ABCD是边长为1的正方形,
∴∠A=∠B=90°,AB=2.
∴∠1+∠2=90°,
∵四边形EFGH为正方形,
∴∠HEF=90°,EH=EF.
∴∠1+∠3=90°,
∴∠2=∠3,
在△AHE与△BEF中,
∵,
∴△AHE≌△BEF(AAS),
∴AE=BF=x,AH=BE=2﹣x,
在Rt△AHE中,由勾股定理得:
EH2=AE2+AH2=x2+(2﹣x)2=2x2﹣4x+4;
即y=2x2﹣4x+4(0<x<2),
故答案为:y=2x2﹣4x+4.
【考点】二次函数的应用.
【分析】设各自抛出后1.1秒时到达相同的最大离地高度为h,这个最大高度为h,则小球的高度y=a(t﹣1.1)2+h,根据题意列出方程即可解决问题.
解:设各自抛出后1.1秒时到达相同的最大离地高度为h,这个最大高度为h,则小球的高度y=a(t﹣1.1)2+h,
由题意a(t﹣1.1)2+h=a(t﹣1﹣1.1)2+h,
解得t=1.6.
故第一个小球抛出后1.6秒时在空中与第二个小球的离地高度相同.
故答案为1.6.
【考点】二次函数的应用
【分析】根据等量关系“四边形APQC的面积=三角形ABC的面积-三角形PBQ的面积”列出函数关系求最小值
解:设P、Q同时出发后经过的时间为t秒,四边形APQC的面积为S平方毫米,
则有:S=S△ABC-S△PBQ
=
=4t2-24t+144
=4(t-3)2+108.
∵4>0
∴当t=3s时,S取得最小值.
三 、解答题
【考点】根据实际问题列二次函数关系式.
【分析】作△ABC的高AD,根据30°角所对的直角边等于斜边的一半得出AD=AB,再根据三角形的面积公式得出△ABC的面积=BC AD,将相关数值代入即可.
解:如图,作△ABC的高AD.
在△ABD中,∵∠ADB=90°,∠B=30°,
∴AD=AB=x,
∴S=△ABC的面积=BC AD=(12﹣x) x=﹣x2+3x,
∴面积S关于x的函数解析式为S=﹣x2+3x(x>0).
点评:本题考查了根据实际问题列二次函数关系式,含30°角的直角三角形的性质,三角形的面积,求出△ABC的高AD是解题的关键.
【考点】二次函数的应用
【分析】设菜园宽为x,则长为30-2x,由面积公式写出y与x的函数关系式,然后利用二次函数的最值的知识可得出菜园的最大面积,及取得最大面积时矩形的长和宽.
解:设矩形的宽为xm,面积为Sm2,根据题意得:
S=x(30-2x)
= -2x2+30x
= -2(x-7.5)2+112.5,
所以当x=7.5时,S最大,最大值为112.5.
30-2x=30-15=15.
【考点】二次函数的应用.
【分析】(1)直接结合图象写出有关点的纵坐标即可;
(2)利用函数的定义直接判断即可.
(3)最高点的纵坐标减去最低点的纵坐标即可求得摩天轮的半径.
解:(1)填表如下:
x(min) 0 3 6 8 12 …
y(m) 5 70 5 54 5 …
(2)因为每给一个x的值有唯一的一个函数值与之对应,符合函数的定义,
所以y是x的函数;
(3)∵最高点为70米,最低点为5米,
∴摩天轮的直径为65米.
【点评】本题考查了二次函数的应用,解题的关键是从实际问题中抽象出函数模型,难度不大.
【考点】二次函数的应用.
【分析】(1)利用网格中数据直接得出乒乓球达到最大高度时的时间;
(2)首先求出函数解析式,进而求出乒乓球落在桌面时,与端点A的水平距离;
(3)①由(2)得乒乓球落在桌面上时,得出对应点坐标,只要利用待定系数法求出函数解析式即可;
②由题意可得,扣杀路线在直线y=x上,由①得,y=a(x﹣3)2﹣a,进而利用根的判别式求出a的值,进而求出x的值.
解:(1)由表格中数据可得,t=0.4(秒),乒乓球达到最大高度;
(2)由表格中数据,可得y是x的二次函数,可设y=a(x﹣1)2+0.45,
将(0,0.25)代入,可得:a=﹣,
则y=﹣(x﹣1)2+0.45,
当y=0时,0=﹣(x﹣1)2+0.45,
解得:x1=,x2=﹣(舍去),
即乒乓球与端点A的水平距离是m;
(3)①由(2)得乒乓球落在桌面上时,对应点为:(,0),
代入y=a(x﹣3)2+k,得(﹣3)2a+k=0,
化简得:k=﹣a;
②由题意可得,扣杀路线在直线y=x上,由①得,y=a(x﹣3)2﹣a,
令a(x﹣3)2﹣a=x,
整理得:20ax2﹣(120a+2)x+175a=0,
当△=(120a+2)2﹣4×20a×175a=0时符合题意,
解方程得:a1=,a2=,
当a1=时,求得x=﹣,不符合题意,舍去;
当a2=时,求得x=,符合题意.
【点评】此题主要考查了二次函数对应用以及根的判别式和一元二次方程的解法等知识,利用图表中数据得出函数解析式是解题关键.
【考点】二次函数的应用.
【分析】(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),于是得到,求得抛物线的解析式为:y=﹣t2+5t+,当t=时,y最大=4.5;
(2)把x=28代入x=10t得t=2.8,当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,于是得到他能将球直接射入球门.
解:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),
∴,
解得:,
∴抛物线的解析式为:y=﹣t2+5t+,
∴当t=时,y最大=4.5;
(2)把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,
∴他能将球直接射入球门.
【点评】本题考查了待定系数法求二次函数的解析式,以及二次函数的应用,正确求得解析式是解题的关键.
【考点】根据实际问题列二次函数关系式;解一元二次方程-因式分解法.
【分析】(1)依题意可得总费用=镜面玻璃费用+边框的费用+加工费用,可得y=6x×30+45+2x2×120化简即可.
(2)根据共花了195元,即玻璃的费用+边框的费用+加工费=195元,即可列出方程求解.
解:(1)y=(2x+2x+x+x)×30+45+2x2×120
=240x2+180x+45;
(2)由题意可列方程为
240x2+180x+45=195,
整理得8x2+6x﹣5=0,即(2x﹣1)(4x+5)=0,
解得x1=0.5,x2=﹣1.25(舍去)
∴x=0.5,
∴2x=1,
答:镜子的长和宽分别是1m和0.5m.
点评:本题是一道一元二次方程的应用题,解这类题关键是理解题意,建立恰当的关系式予以求解.
【考点】二次函数的应用
【分析】(1)求得直线y=3x+3与坐标轴的两交点坐标,然后根据OB=OA即可求得点B的坐标,然后利用待定系数法求得经过A、B、C三点的抛物线的解析式即可;
(2)本问关键是求出△ABP的面积表达式.这个表达式是一个关于P点横坐标的二次函数,利用二次函数求极值的方法可以确定P点的坐标.
解:(1)令y=0得:3x+3=0,x= -1,
故点C的坐标为(-1,0);
令x=0得:y=3x+3=3×0+3=3
故点A的坐标为(0,3);
∵△OAB是等腰直角三角形.
∴ OB=OA=3,
∴点B的坐标为(3,0),
设过A、B、C三点的抛物线的解析式y=ax2+bx+c,
解得:
∴解析式为:y= -x2+2x+3;
(2)存在.如图1所示,设P(x,y)是第一象限的抛物线上一点,
过点P作PN⊥x轴于点N,则ON=x,PN=y,BN=OB-ON=3-x.
S△ABP=S梯形PNOA+S△PNB-S△AOB
=(OA+PN)ON+PNBN - OA×OB
=
=
∵P(x,y)在抛物线上,∴y= -x2+2x+3,代入上式得:
S△ABP== (x2-3x)=
∴当x= 时,S△ABP取得最大值.
当x=时,y= -x2+2x+3= ,
∴P( ).
所以,在第一象限的抛物线上,存在一点P,使得△ABP的面积最大;
P点的坐标为()
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
