2018-2019学年高二物理粤教版选修3-1学案:第1章 章末总结
文档属性
| 名称 | 2018-2019学年高二物理粤教版选修3-1学案:第1章 章末总结 |  | |
| 格式 | zip | ||
| 文件大小 | 413.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-09-03 20:10:11 | ||
图片预览

文档简介
章末总结
一、电场的力的性质
1.库仑力实质上就是电场力,与重力、弹力一样,它也是一种基本力.带电粒子在电场中的平衡问题实际上属于力学平衡问题,只是多了一个电场力而已.
2.电场力作用下带电体的平衡和加速问题的分析步骤是:先进行正确的受力分析,然后利用平衡条件或牛顿第二定律求解,主要方法有合成法、正交分解法等.
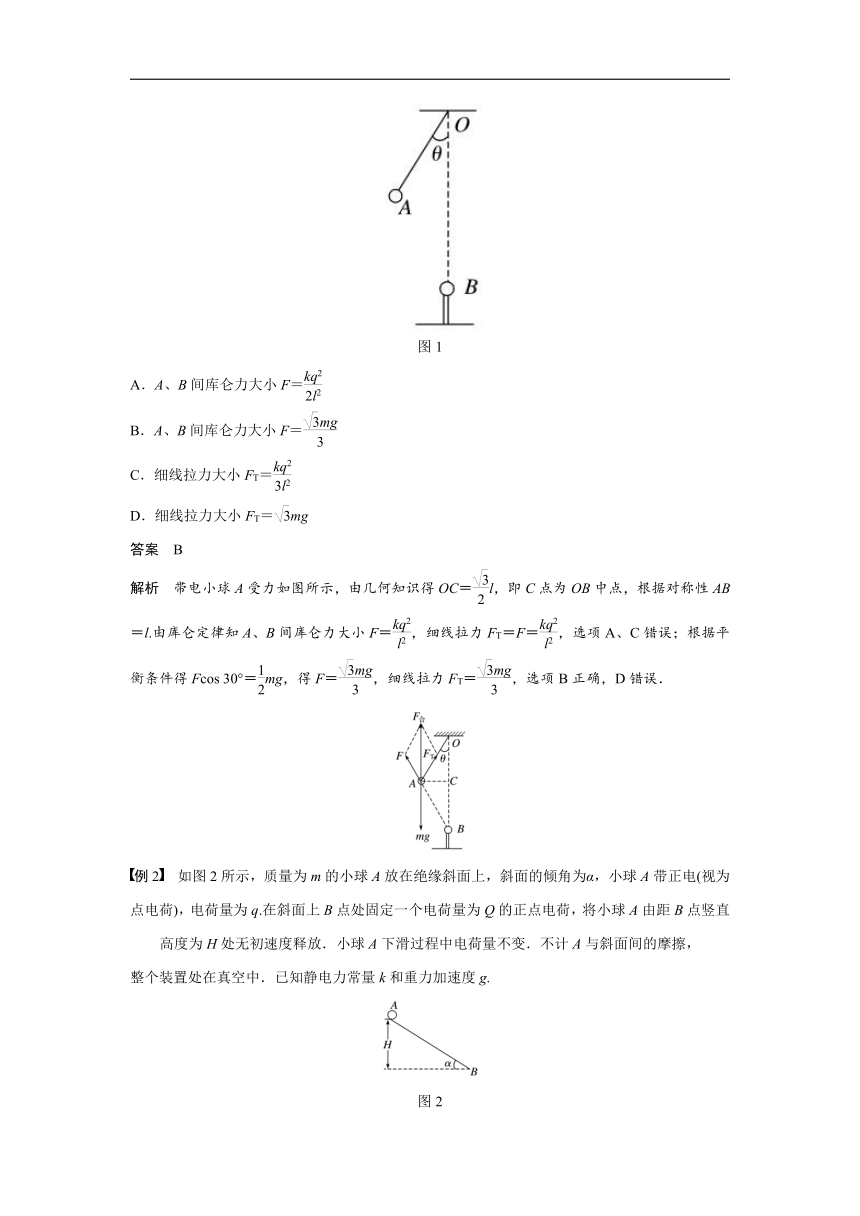
例1 如图1所示,质量为m、电荷量为q的带电小球A用绝缘细线悬挂于O点,带有电荷量也为q的小球B固定在O点正下方绝缘柱上.其中O点与小球A的间距为l,O点与小球B的间距为l.当小球A平衡时,悬线与竖直方向夹角θ=30°.带电小球A、B均可视为点电荷.静电力常量为k,则( )
图1
A.A、B间库仑力大小F=
B.A、B间库仑力大小F=
C.细线拉力大小FT=
D.细线拉力大小FT=mg
答案 B
解析 带电小球A受力如图所示,由几何知识得OC=l,即C点为OB中点,根据对称性AB=l.由库仑定律知A、B间库仑力大小F=,细线拉力FT=F=,选项A、C错误;根据平衡条件得Fcos 30°=mg,得F=,细线拉力FT=,选项B正确,D错误.
例2 如图2所示,质量为m的小球A放在绝缘斜面上,斜面的倾角为α,小球A带正电(视为点电荷),电荷量为q.在斜面上B点处固定一个电荷量为Q的正点电荷,将小球A由距B点竖直高度为H处无初速度释放.小球A下滑过程中电荷量不变.不计A与斜面间的摩擦,
整个装置处在真空中.已知静电力常量k和重力加速度g.
图2
(1)A球刚释放时的加速度是多大?
(2)当A球的动能最大时,求此时A球与B点的距离.
答案 (1)gsin α- (2)
解析 (1)根据牛顿第二定律mgsin α-F=ma
根据库仑定律:F=k,r=
联立以上各式解得a=gsin α-.
(2)当A球受到的合力为零、加速度为零时,速度最大,动能最大.设此时A球与B点间的距离为d,则mgsin α=,解得d= .
二、电场的能的性质
电荷在电场中具有电势能,正电荷在电势高的地方电势能大,负电荷在电势低的地方电势能大.电场力做功引起电势能的变化,电场力做正功,电荷的电势能减小,电场力做负功,电荷的电势能增大.
例3 如图3所示,在粗糙程度相同的绝缘水平面上固定一个点电荷Q,在M点无初速度释放一个带有恒定电荷量的小物块,小物块在Q的电场中沿水平面运动到N点停止,则从M到N的过程中,下列说法错误的是( )
图3
A.小物块所受的静电力逐渐减小
B.小物块具有的电势能逐渐减小
C.M点的电势一定高于N点的电势
D.小物块电势能的减少量一定等于克服摩擦力做的功
答案 C
解析 小物块在从M运动到N的过程中,一定受到向右的摩擦力,所以静电力一定向左.由M运动到N,离电荷Q距离越来越大,所以小物块受到的静电力一定减小,A正确;由动能定理可得μmgx-WE=0,即WE=μmgx,静电力做正功,小物块具有的电势能减小,其减少量等于克服滑动摩擦力做的功,B、D正确;因点电荷Q的电性未知,不能判断M、N两点电势的高低,C错误.
例4 (多选)空间某一静电场的电势φ在x轴上的分布如图4所示,x轴上两点B、C的电场强度在x轴方向上的分量分别是EBx、ECx,下列说法中正确的有( )
图4
A.EBx的大小大于ECx的大小
B.EBx的方向沿x轴正方向
C.电荷在O点受到的电场力在x轴方向上的分量最大
D.负电荷沿x轴从B移到C的过程中,电场力先做正功后做负功
答案 AD
解析 在B点和C点附近分别取很小的一段距离d,由题图可知,B点段对应的电势差大于C点段对应的电势差,若将这两段的电场看做匀强电场,则有E=,可见EBx>ECx,选项A正确;同理可知O点场强在x轴方向上的分量最小,电荷在该点受到的电场力在x轴方向上的分量最小,选项C错误;沿电场方向电势降低,在O点左侧,Ex的方向沿x轴负方向,在O点右侧,Ex的方向沿x轴正方向,所以选项B错误;负电荷沿x轴从B到C过程中,电势能先减小后增大,故电场力先做正功后做负功,D正确.
三、带电体在复合场中的运动
1.带电体在复合场中的运动是指带电体在运动过程中同时受到电场力及其他力的作用.较常见的是在运动过程中,带电体同时受到重力和电场力的作用.
2.由于带电体在复合场中的运动是一个综合电场力、电势能的力学问题,研究的方法与质点动力学的研究方法相同,它同样遵循运动的合成与分解、力的独立作用原理、牛顿运动定律、动能定理、功能关系等力学规律.
例5 如图5所示,ABCDF为竖直放在场强为E=104 V/m的水平匀强电场中的绝缘光滑轨道.其中轨道的BCDF部分是半径为R=0.2 m的圆形轨道,轨道的水平部分与圆相切于B点,A为水平轨道上的一点,而且AB之间的距离s=0.6 m,把一质量m=0.1 kg、带电荷量q=+1×10-4 C的小球放在水平轨道的A点由静止开始释放,小球在轨道的内侧运动.求:(g取10 m/s2)
图5
(1)小球到达B点时速度的大小;
(2)小球到达D点时对轨道的压力;
(3)若让小球安全通过轨道,求开始释放点离B点的最小距离.(结果保留两位有效数字)
答案 (1)2 m/s (2)1 N,方向竖直向上 (3)0.62 m
解析 (1)小球从A到B,由动能定理有qEs=mvB2-0,
解得vB=2 m/s.
(2)小球从A到D,由动能定理有qEs-2mgR=mvD2-0,解得vD=2 m/s.
小球在D点,由牛顿第二定律有mg+FN=m,
解得FN=1 N,方向竖直向下,由牛顿第三定律得小球对轨道的压力大小为1 N,方向竖直向上.
(3)小球受到的竖直向下的重力和水平向右的电场力大小相等,这两个力的合力为F=mg= N,与水平方向的夹角θ=45°,如图所示.
设小球在竖直平面内做圆周运动的等效最高点为G点,小球在G点的最小速度为vG,由牛顿第二定律有F=m,
小球从A到G,由动能定理有qE(s′-Rcos θ)-mg(R+Rsin θ)=mvG2-0,
联立解得s′≈0.62 m.
一、电场的力的性质
1.库仑力实质上就是电场力,与重力、弹力一样,它也是一种基本力.带电粒子在电场中的平衡问题实际上属于力学平衡问题,只是多了一个电场力而已.
2.电场力作用下带电体的平衡和加速问题的分析步骤是:先进行正确的受力分析,然后利用平衡条件或牛顿第二定律求解,主要方法有合成法、正交分解法等.
例1 如图1所示,质量为m、电荷量为q的带电小球A用绝缘细线悬挂于O点,带有电荷量也为q的小球B固定在O点正下方绝缘柱上.其中O点与小球A的间距为l,O点与小球B的间距为l.当小球A平衡时,悬线与竖直方向夹角θ=30°.带电小球A、B均可视为点电荷.静电力常量为k,则( )
图1
A.A、B间库仑力大小F=
B.A、B间库仑力大小F=
C.细线拉力大小FT=
D.细线拉力大小FT=mg
答案 B
解析 带电小球A受力如图所示,由几何知识得OC=l,即C点为OB中点,根据对称性AB=l.由库仑定律知A、B间库仑力大小F=,细线拉力FT=F=,选项A、C错误;根据平衡条件得Fcos 30°=mg,得F=,细线拉力FT=,选项B正确,D错误.
例2 如图2所示,质量为m的小球A放在绝缘斜面上,斜面的倾角为α,小球A带正电(视为点电荷),电荷量为q.在斜面上B点处固定一个电荷量为Q的正点电荷,将小球A由距B点竖直高度为H处无初速度释放.小球A下滑过程中电荷量不变.不计A与斜面间的摩擦,
整个装置处在真空中.已知静电力常量k和重力加速度g.
图2
(1)A球刚释放时的加速度是多大?
(2)当A球的动能最大时,求此时A球与B点的距离.
答案 (1)gsin α- (2)
解析 (1)根据牛顿第二定律mgsin α-F=ma
根据库仑定律:F=k,r=
联立以上各式解得a=gsin α-.
(2)当A球受到的合力为零、加速度为零时,速度最大,动能最大.设此时A球与B点间的距离为d,则mgsin α=,解得d= .
二、电场的能的性质
电荷在电场中具有电势能,正电荷在电势高的地方电势能大,负电荷在电势低的地方电势能大.电场力做功引起电势能的变化,电场力做正功,电荷的电势能减小,电场力做负功,电荷的电势能增大.
例3 如图3所示,在粗糙程度相同的绝缘水平面上固定一个点电荷Q,在M点无初速度释放一个带有恒定电荷量的小物块,小物块在Q的电场中沿水平面运动到N点停止,则从M到N的过程中,下列说法错误的是( )
图3
A.小物块所受的静电力逐渐减小
B.小物块具有的电势能逐渐减小
C.M点的电势一定高于N点的电势
D.小物块电势能的减少量一定等于克服摩擦力做的功
答案 C
解析 小物块在从M运动到N的过程中,一定受到向右的摩擦力,所以静电力一定向左.由M运动到N,离电荷Q距离越来越大,所以小物块受到的静电力一定减小,A正确;由动能定理可得μmgx-WE=0,即WE=μmgx,静电力做正功,小物块具有的电势能减小,其减少量等于克服滑动摩擦力做的功,B、D正确;因点电荷Q的电性未知,不能判断M、N两点电势的高低,C错误.
例4 (多选)空间某一静电场的电势φ在x轴上的分布如图4所示,x轴上两点B、C的电场强度在x轴方向上的分量分别是EBx、ECx,下列说法中正确的有( )
图4
A.EBx的大小大于ECx的大小
B.EBx的方向沿x轴正方向
C.电荷在O点受到的电场力在x轴方向上的分量最大
D.负电荷沿x轴从B移到C的过程中,电场力先做正功后做负功
答案 AD
解析 在B点和C点附近分别取很小的一段距离d,由题图可知,B点段对应的电势差大于C点段对应的电势差,若将这两段的电场看做匀强电场,则有E=,可见EBx>ECx,选项A正确;同理可知O点场强在x轴方向上的分量最小,电荷在该点受到的电场力在x轴方向上的分量最小,选项C错误;沿电场方向电势降低,在O点左侧,Ex的方向沿x轴负方向,在O点右侧,Ex的方向沿x轴正方向,所以选项B错误;负电荷沿x轴从B到C过程中,电势能先减小后增大,故电场力先做正功后做负功,D正确.
三、带电体在复合场中的运动
1.带电体在复合场中的运动是指带电体在运动过程中同时受到电场力及其他力的作用.较常见的是在运动过程中,带电体同时受到重力和电场力的作用.
2.由于带电体在复合场中的运动是一个综合电场力、电势能的力学问题,研究的方法与质点动力学的研究方法相同,它同样遵循运动的合成与分解、力的独立作用原理、牛顿运动定律、动能定理、功能关系等力学规律.
例5 如图5所示,ABCDF为竖直放在场强为E=104 V/m的水平匀强电场中的绝缘光滑轨道.其中轨道的BCDF部分是半径为R=0.2 m的圆形轨道,轨道的水平部分与圆相切于B点,A为水平轨道上的一点,而且AB之间的距离s=0.6 m,把一质量m=0.1 kg、带电荷量q=+1×10-4 C的小球放在水平轨道的A点由静止开始释放,小球在轨道的内侧运动.求:(g取10 m/s2)
图5
(1)小球到达B点时速度的大小;
(2)小球到达D点时对轨道的压力;
(3)若让小球安全通过轨道,求开始释放点离B点的最小距离.(结果保留两位有效数字)
答案 (1)2 m/s (2)1 N,方向竖直向上 (3)0.62 m
解析 (1)小球从A到B,由动能定理有qEs=mvB2-0,
解得vB=2 m/s.
(2)小球从A到D,由动能定理有qEs-2mgR=mvD2-0,解得vD=2 m/s.
小球在D点,由牛顿第二定律有mg+FN=m,
解得FN=1 N,方向竖直向下,由牛顿第三定律得小球对轨道的压力大小为1 N,方向竖直向上.
(3)小球受到的竖直向下的重力和水平向右的电场力大小相等,这两个力的合力为F=mg= N,与水平方向的夹角θ=45°,如图所示.
设小球在竖直平面内做圆周运动的等效最高点为G点,小球在G点的最小速度为vG,由牛顿第二定律有F=m,
小球从A到G,由动能定理有qE(s′-Rcos θ)-mg(R+Rsin θ)=mvG2-0,
联立解得s′≈0.62 m.
同课章节目录
- 第一章 电场
- 第01节 认识电场
- 第02节 探究静电力
- 第03节 电场强度
- 第04节 电势和电势差
- 第05节 电场强度与电势差的关系
- 第06节 示波器的奥秘
- 第07节 了解电容器
- 第08节 静电与新技术
- 第二章 电路
- 第01节 探究决定导线电阻的因素
- 第02节 对电阻的进一步研究
- 第03节 研究闭合电路
- 第04节 认识多用电表
- 第05节 电功率
- 第06节 走进门电路
- 第07节 了解集成电路
- 8.多用电表
- 9.实验:测定电池的电动势和内阻
- 10.简单的逻辑电路
- 第三章 磁场
- 第01节 我们周围的磁象
- 第02节 认识磁场
- 第03节 探究安培力
- 第04节 安培力的应用
- 第05节 研究洛仑兹力
- 第06节 洛仑兹力与现代技术
