八年级数学上册第三章3.3勾股定理的应用知识点与同步训练(含解析)
文档属性
| 名称 | 八年级数学上册第三章3.3勾股定理的应用知识点与同步训练(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 246.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-03 20:55:19 | ||
图片预览




文档简介
勾股定理的应用
一.求线段长
常用的方法有:
1.直接利用勾股定理:已知直角三角形的两条边,求另外一条;
2.通过设未知数,根据勾股定理列方程,解方程;
3.通过特殊三角形的比例关系来计算(仅限于选择、填空题中的快速计算);
如图1,;如图2,
4.面积法:当所求的线段为三角形的高时,利用面积相等可求得对应高的长度;
如上图,,.
5.挖掘题目中的隐含条件,通过全等三角形、等腰三角形等来求线段长;
6.做辅助线:根据题目中的条件,添加适当的辅助线,如垂直等进而解三角形.
二.勾股定理与最短距离
在立体图形中,往往会涉及到求某两点之间的最短路程问题,这就需要我们画出立体图形的展开图,然后利用“两点之间线段最短”和“勾股定理”求出最短距离.
三.两点间距离公式
在平面直角坐标系中,任意给定两点,.过点A、B分别向坐标轴作垂线,则,,由勾股定理可得,.(初中阶段解答题中不能直接应用,如果需要,应提前说明“由勾股定理得”)
一.考点:1.求线段长;2.最短路径问题;3.两点之间距离公式.
二.重难点:根据已知条件,分析相应图形,并选取合适的方法,求线段长.
三.易错点:
1.在应用勾股定理的过程中,注意分清楚直角边和斜边,选择正确的公式来进行计算;
2.所对的直角边是斜边的一半,注意分清楚“所对的直角边”和“斜边”.
题模一:求线段长
例2.1.1 在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A.
B.
C.
D.
【答案】A
【解析】
根据题意画出相应的图形,如图所示:
在Rt△ABC中,AC=9,BC=12,
根据勾股定理得:AB==15,
过C作CD⊥AB,交AB于点D,
又S△ ABC=AC?BC=AB?CD,
∴CD===,
则点C到AB的距离是.
故选A
例2.1.2 如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是( )
A. 2
B. 2
C. 4
D. 4
【答案】A
【解析】 ∵∠A=30°,∠B=90°,
∴∠ACB=180°﹣30°﹣90°=60°,
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠A=∠ACD=30°,
∴∠DCB=60°﹣30°=30°,
∵BD=1,
∴CD=2=AD,
∴AB=1+2=3,
在△BCD中,由勾股定理得:CB=,
在△ABC中,由勾股定理得:AC==2,
故选:A.
例2.1.3 如图,直线l过等腰直角三角形ABC顶点B,A、C两点到直线l的距离分别是2和3,则AB的长是( )
A. 5
B.
C.
D.
【答案】D
【解析】 此题考查了全等三角形的判定与性质,等腰直角三角形的性质,以及勾股定理,利用了转化的数学思想,灵活运用全等三角形的判定与性质是解本题的关键.
如图所示:
∵△ABC为等腰直角三角形,
∴AB=BC,∠ABC=90°,
∴∠ABD+∠CBE=90°,
又AD⊥BD,∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∴∠CBE=∠DAB,
在△ABD和△BCE中,
,
∴△ABD≌△BCE,
∴BD=CE,又CE=3,
∴BD=3,
在Rt△ABD中,AD=2,BD=3,
根据勾股定理得:AB==.
故选D
例2.1.4 如图,有一块直角三角形纸片,两直角边cm,cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A. 2cm
B. 3cm
C. 4cm
D. 5cm
【答案】B
【解析】 该题考查的是勾股定理的计算.
∵,,,
∴,
∵,∴,
设,则在Rt△DEB中,
,故,
故选B.
题模二:最短路径问题
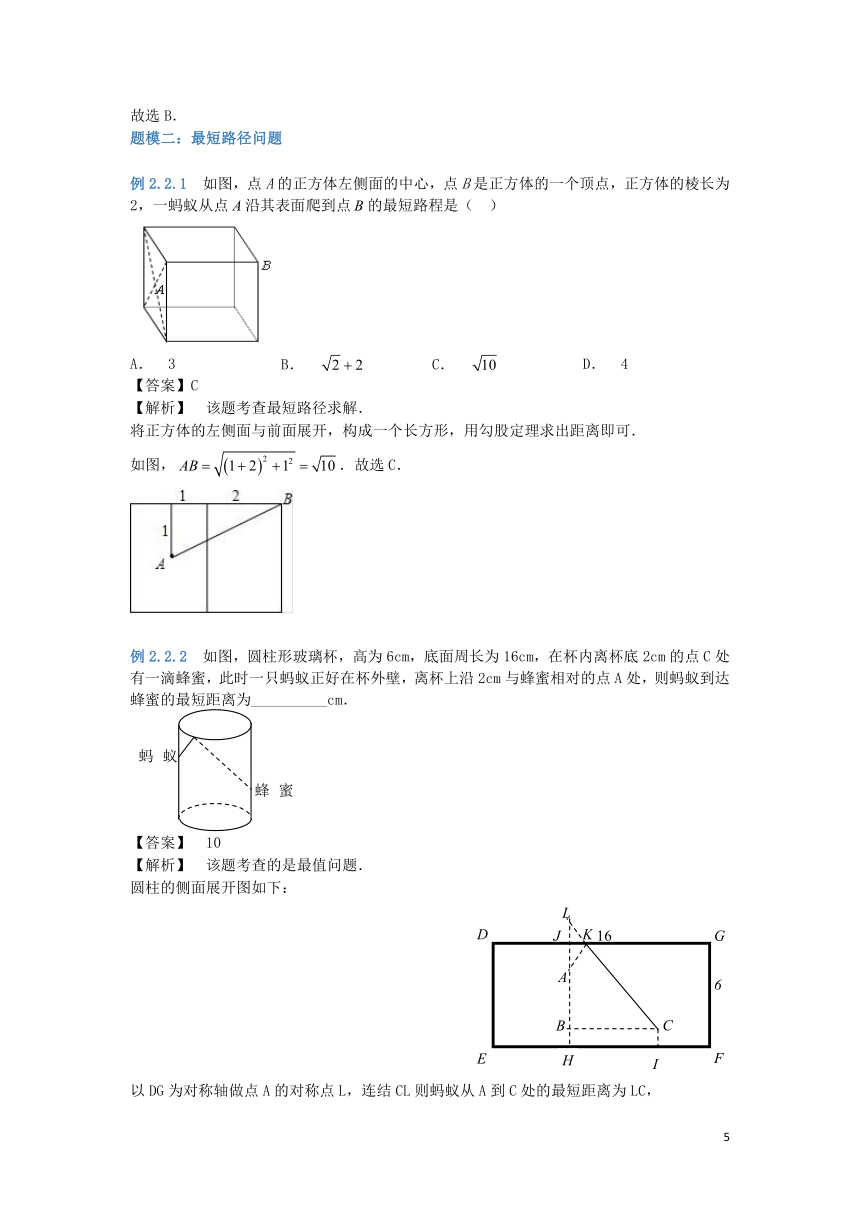
例2.2.1 如图,点A的正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点沿其表面爬到点的最短路程是( )
A. 3
B.
C.
D. 4
【答案】C
【解析】 该题考查最短路径求解.
将正方体的左侧面与前面展开,构成一个长方形,用勾股定理求出距离即可.
如图,.故选C.
例2.2.2 如图,圆柱形玻璃杯,高为6cm,底面周长为16cm,在杯内离杯底2cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为__________cm.
【答案】 10
【解析】 该题考查的是最值问题.
圆柱的侧面展开图如下:
以DG为对称轴做点A的对称点L,连结CL则蚂蚁从A到C处的最短距离为LC,
根据轴对称性质可得△LJK≌△AJK,又由题意得,
∵,
∴,
∴Rt△LBC中,,
∴,即蚂蚁到达蜂蜜处的最短距离为.
例2.2.3 如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20cm,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为 m.(π取3)
【答案】 10
【解析】 其侧面展开图如图:作点C关于AB的对称点F,连接DF,
∵中间可供滑行的部分的截面是半径为5m的半圆,∴BC=πR=5π=15m,AB=CD=20m,∴CF=30m,在Rt△CDF中,DF=m,故他滑行的最短距离约为10m.
题模三:两点之间距离公式
例2.3.1 在一次“寻宝”人找到了如图所示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都是,则“宝藏”点的坐标是( )
A. (1,0)
B. (5,4)
C. (1,0)或(5,4)
D. (0,1)或(4,5)
【答案】C
【解析】 本题考查了坐标的确定及利用两点的坐标确定两点之间的距离公式,是一道中难度题.
根据两点之间的距离公式,d=,将四个选项代入公式中,观察哪一个等于,再作答.
设宝藏的坐标点为C(x,y),
根据坐标系中两点间距离公式可知,AC=BC,
则(x-2)2+(y-3)2=(x-4)2+(y-1)2,
化简得x-y=1;
又因为标志点到“宝藏”点的距离是,
所以(x-2)2+(y-3)2=10;
把x=1+y代入方程得,y=0或y=4,即x=1或5,
所以“宝藏”C点的坐标是(1,0)或(5,4).
故选C.
随练2.1 已知一个直角三角形的两条直角边分别为6cm,8cm,那么这个直角三角形斜边上的高为 cm.
【答案】 4.8
【解析】 ∵直角三角形的两条直角边分别为6cm,8cm,∴斜边为=10,设斜边上的高为h,则直角三角形的面积为×6×8=×10h,h=4.8cm,这个直角三角形斜边上的高为4.8cm.
随练2.2 在Rt△ABC中,∠ACB=90,∠BAC=30°,BC=2,以斜边AB为一边,作等边△ABD,则线段CD的长为__________.
【答案】 2或
【解析】 本题考察的是解三角形.
如图,由,知..
①当D与C分居直线AB两侧时,,由勾股定理,
.
②若,故在BC的延长线上.那么
随练2.3 △ABC中,AB=13,AC=15,BC边上的高AD=12,则BC=____________
【答案】 14或4
【解析】 该题考查勾股定理.
①如图,锐角△ABC中,
,,BC边上高,
在Rt△ABD中,,由勾股定理得:
∴,
在Rt△ACD中,,由勾股定理得:
,
∴,
∴BC的长为
②钝角△ABC中,
,,BC边上高,
在Rt△ABD中,,由勾股定理得:
,
∴,
在Rt△ACD中:,,由勾股定理得:
,
∴,
∴BC的长为
综上可知答案为:14或4
随练2.4 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
A. 3
B. 4
C. 5
D. 6
【答案】A
【解析】
过D点作DE⊥BC于E.
∵∠A=90°,AB=4,BD=5,
∴AD===3,
∵BD平分∠ABC,∠A=90°,
∴点D到BC的距离=AD=3.
故选A.
随练2.5 如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要____cm;如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要____cm.
【答案】 (1)10 (2)2
【解析】
将长方体展开,连接A、B,
根据两点之间线段最短,AB==10(cm);
如果从点A开始经过4个侧面缠绕n圈到达点B,
相当于直角三角形的两条直角边分别是8n和6,
根据勾股定理可知所用细线最短需要==2(cm).
故答案为:10;2.
随练2.6 在平面直角坐标系中,已知点A(-,0),B(,0),点C在坐标轴上,且AC+BC=6,写出满足条件的所有点C的坐标____.
【答案】 (0,2),(0,-2),(-3,0),(3,0)
【解析】 本题考查了勾股定理、坐标与图形的性质.解题时,要分类讨论,以防漏解.另外,当点C在y轴上时,也可以根据两点间的距离公式来求点C的坐标.
需要分类讨论:①当点C位于x轴上时,根据线段间的和差关系即可求得点C的坐标;②当点C位于y轴上时,根据勾股定理求点C的坐标.
如图,①当点C位于y轴上时,设C(0,b).
则+=6,解得,b=2或b=-2,
此时C(0,2),或C(0,-2).
如图,②当点C位于x轴上时,设C(a,0).
则|--a|+|a-|=6,即2a=6或-2a=6,
解得a=3或a=-3,
此时C(-3,0),或C(3,0).
综上所述,点C的坐标是:(0,2),(0,-2),(-3,0),(3,0).
故答案是:(0,2),(0,-2),(-3,0),(3,0).
一.求线段长
常用的方法有:
1.直接利用勾股定理:已知直角三角形的两条边,求另外一条;
2.通过设未知数,根据勾股定理列方程,解方程;
3.通过特殊三角形的比例关系来计算(仅限于选择、填空题中的快速计算);
如图1,;如图2,
4.面积法:当所求的线段为三角形的高时,利用面积相等可求得对应高的长度;
如上图,,.
5.挖掘题目中的隐含条件,通过全等三角形、等腰三角形等来求线段长;
6.做辅助线:根据题目中的条件,添加适当的辅助线,如垂直等进而解三角形.
二.勾股定理与最短距离
在立体图形中,往往会涉及到求某两点之间的最短路程问题,这就需要我们画出立体图形的展开图,然后利用“两点之间线段最短”和“勾股定理”求出最短距离.
三.两点间距离公式
在平面直角坐标系中,任意给定两点,.过点A、B分别向坐标轴作垂线,则,,由勾股定理可得,.(初中阶段解答题中不能直接应用,如果需要,应提前说明“由勾股定理得”)
一.考点:1.求线段长;2.最短路径问题;3.两点之间距离公式.
二.重难点:根据已知条件,分析相应图形,并选取合适的方法,求线段长.
三.易错点:
1.在应用勾股定理的过程中,注意分清楚直角边和斜边,选择正确的公式来进行计算;
2.所对的直角边是斜边的一半,注意分清楚“所对的直角边”和“斜边”.
题模一:求线段长
例2.1.1 在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A.
B.
C.
D.
【答案】A
【解析】
根据题意画出相应的图形,如图所示:
在Rt△ABC中,AC=9,BC=12,
根据勾股定理得:AB==15,
过C作CD⊥AB,交AB于点D,
又S△ ABC=AC?BC=AB?CD,
∴CD===,
则点C到AB的距离是.
故选A
例2.1.2 如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是( )
A. 2
B. 2
C. 4
D. 4
【答案】A
【解析】 ∵∠A=30°,∠B=90°,
∴∠ACB=180°﹣30°﹣90°=60°,
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠A=∠ACD=30°,
∴∠DCB=60°﹣30°=30°,
∵BD=1,
∴CD=2=AD,
∴AB=1+2=3,
在△BCD中,由勾股定理得:CB=,
在△ABC中,由勾股定理得:AC==2,
故选:A.
例2.1.3 如图,直线l过等腰直角三角形ABC顶点B,A、C两点到直线l的距离分别是2和3,则AB的长是( )
A. 5
B.
C.
D.
【答案】D
【解析】 此题考查了全等三角形的判定与性质,等腰直角三角形的性质,以及勾股定理,利用了转化的数学思想,灵活运用全等三角形的判定与性质是解本题的关键.
如图所示:
∵△ABC为等腰直角三角形,
∴AB=BC,∠ABC=90°,
∴∠ABD+∠CBE=90°,
又AD⊥BD,∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∴∠CBE=∠DAB,
在△ABD和△BCE中,
,
∴△ABD≌△BCE,
∴BD=CE,又CE=3,
∴BD=3,
在Rt△ABD中,AD=2,BD=3,
根据勾股定理得:AB==.
故选D
例2.1.4 如图,有一块直角三角形纸片,两直角边cm,cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
A. 2cm
B. 3cm
C. 4cm
D. 5cm
【答案】B
【解析】 该题考查的是勾股定理的计算.
∵,,,
∴,
∵,∴,
设,则在Rt△DEB中,
,故,
故选B.
题模二:最短路径问题
例2.2.1 如图,点A的正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点沿其表面爬到点的最短路程是( )
A. 3
B.
C.
D. 4
【答案】C
【解析】 该题考查最短路径求解.
将正方体的左侧面与前面展开,构成一个长方形,用勾股定理求出距离即可.
如图,.故选C.
例2.2.2 如图,圆柱形玻璃杯,高为6cm,底面周长为16cm,在杯内离杯底2cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为__________cm.
【答案】 10
【解析】 该题考查的是最值问题.
圆柱的侧面展开图如下:
以DG为对称轴做点A的对称点L,连结CL则蚂蚁从A到C处的最短距离为LC,
根据轴对称性质可得△LJK≌△AJK,又由题意得,
∵,
∴,
∴Rt△LBC中,,
∴,即蚂蚁到达蜂蜜处的最短距离为.
例2.2.3 如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为5m的半圆,其边缘AB=CD=20cm,小明要在AB上选取一点E,能够使他从点D滑到点E再到点C的滑行距离最短,则他滑行的最短距离为 m.(π取3)
【答案】 10
【解析】 其侧面展开图如图:作点C关于AB的对称点F,连接DF,
∵中间可供滑行的部分的截面是半径为5m的半圆,∴BC=πR=5π=15m,AB=CD=20m,∴CF=30m,在Rt△CDF中,DF=m,故他滑行的最短距离约为10m.
题模三:两点之间距离公式
例2.3.1 在一次“寻宝”人找到了如图所示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都是,则“宝藏”点的坐标是( )
A. (1,0)
B. (5,4)
C. (1,0)或(5,4)
D. (0,1)或(4,5)
【答案】C
【解析】 本题考查了坐标的确定及利用两点的坐标确定两点之间的距离公式,是一道中难度题.
根据两点之间的距离公式,d=,将四个选项代入公式中,观察哪一个等于,再作答.
设宝藏的坐标点为C(x,y),
根据坐标系中两点间距离公式可知,AC=BC,
则(x-2)2+(y-3)2=(x-4)2+(y-1)2,
化简得x-y=1;
又因为标志点到“宝藏”点的距离是,
所以(x-2)2+(y-3)2=10;
把x=1+y代入方程得,y=0或y=4,即x=1或5,
所以“宝藏”C点的坐标是(1,0)或(5,4).
故选C.
随练2.1 已知一个直角三角形的两条直角边分别为6cm,8cm,那么这个直角三角形斜边上的高为 cm.
【答案】 4.8
【解析】 ∵直角三角形的两条直角边分别为6cm,8cm,∴斜边为=10,设斜边上的高为h,则直角三角形的面积为×6×8=×10h,h=4.8cm,这个直角三角形斜边上的高为4.8cm.
随练2.2 在Rt△ABC中,∠ACB=90,∠BAC=30°,BC=2,以斜边AB为一边,作等边△ABD,则线段CD的长为__________.
【答案】 2或
【解析】 本题考察的是解三角形.
如图,由,知..
①当D与C分居直线AB两侧时,,由勾股定理,
.
②若,故在BC的延长线上.那么
随练2.3 △ABC中,AB=13,AC=15,BC边上的高AD=12,则BC=____________
【答案】 14或4
【解析】 该题考查勾股定理.
①如图,锐角△ABC中,
,,BC边上高,
在Rt△ABD中,,由勾股定理得:
∴,
在Rt△ACD中,,由勾股定理得:
,
∴,
∴BC的长为
②钝角△ABC中,
,,BC边上高,
在Rt△ABD中,,由勾股定理得:
,
∴,
在Rt△ACD中:,,由勾股定理得:
,
∴,
∴BC的长为
综上可知答案为:14或4
随练2.4 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
A. 3
B. 4
C. 5
D. 6
【答案】A
【解析】
过D点作DE⊥BC于E.
∵∠A=90°,AB=4,BD=5,
∴AD===3,
∵BD平分∠ABC,∠A=90°,
∴点D到BC的距离=AD=3.
故选A.
随练2.5 如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要____cm;如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要____cm.
【答案】 (1)10 (2)2
【解析】
将长方体展开,连接A、B,
根据两点之间线段最短,AB==10(cm);
如果从点A开始经过4个侧面缠绕n圈到达点B,
相当于直角三角形的两条直角边分别是8n和6,
根据勾股定理可知所用细线最短需要==2(cm).
故答案为:10;2.
随练2.6 在平面直角坐标系中,已知点A(-,0),B(,0),点C在坐标轴上,且AC+BC=6,写出满足条件的所有点C的坐标____.
【答案】 (0,2),(0,-2),(-3,0),(3,0)
【解析】 本题考查了勾股定理、坐标与图形的性质.解题时,要分类讨论,以防漏解.另外,当点C在y轴上时,也可以根据两点间的距离公式来求点C的坐标.
需要分类讨论:①当点C位于x轴上时,根据线段间的和差关系即可求得点C的坐标;②当点C位于y轴上时,根据勾股定理求点C的坐标.
如图,①当点C位于y轴上时,设C(0,b).
则+=6,解得,b=2或b=-2,
此时C(0,2),或C(0,-2).
如图,②当点C位于x轴上时,设C(a,0).
则|--a|+|a-|=6,即2a=6或-2a=6,
解得a=3或a=-3,
此时C(-3,0),或C(3,0).
综上所述,点C的坐标是:(0,2),(0,-2),(-3,0),(3,0).
故答案是:(0,2),(0,-2),(-3,0),(3,0).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
