2018版高中物理第5章力与平衡第2节力的分解课件鲁科版必修1:37张PPT
文档属性
| 名称 | 2018版高中物理第5章力与平衡第2节力的分解课件鲁科版必修1:37张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-09-04 12:59:27 | ||
图片预览










文档简介
课件37张PPT。第2节 力的分解教师备课参考 |核心素养养成目标|物理观念
1.知道分力和力的分解的概念.
2.理解力的分解是力的合成的逆运算,掌握分解力的方法.
3.能应用力的分解分析生产和生活中的相关问题.
科学思维与科学探究
1.体会等效替代的物理思想在探究自然规律中的作用,通过多举例、多演示,让学生将生活实际与物理概念相联系,通过实例分析掌握力的效果分解法和正交分解法.
2.结合三角形定则掌握图解法求分力、合力的技巧.
科学态度与责任
1.通过力的分解的学习,体会物理规律与生活的联系.
2.进一步渗透等效替代的物理思想.|教学重难点|教学重点
分力的求解.
教学难点
1.力的分解的讨论.
2.力的分解方法的应用.感悟解题规律探寻基本知识测评学习效果探寻基本知识·树立物理观念知识点一 分力 力的分解【情境导学】
为了行车方便和安全,高大的桥往往有很长的引桥.
问题:(1)在引桥上,汽车重力有什么作用效果?
(2)从力的分解的角度分析,引桥很长有什么好处?答案: (1)汽车重力的两个作用效果是垂直桥面向下使汽车压斜面和沿桥面向下使汽车下滑或阻碍汽车上行.
(2)高大的桥建造很长的引桥可以减小汽车重力沿斜面向下的分力,使行车更安全.【知识梳理】
1.分力:几个力共同作用的效果与一个力的作用效果相同,则这几个力叫那个力的分力.
2.力的分解
求一个已知力的 叫做力的分解.
3.力的分解法则
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的邻边就表示力F的两个分力F1,F2.
【思考判断】
1.一个力只能分解为一组分力.( )
2.力的分解遵循平行四边形定则.( )
3.某个分力的大小不可能大于合力.( )分力×√×知识点二力的正交分解与力的分解的应用【情境导学】已知竖直平面内有一个大小为10 N的力作用于O点,该力与x轴正方向之间的夹角为30°,与y轴正方向之间的夹角为60°,现将它分解到x轴和y轴方向上,则x轴和y轴上的分力Fx和Fy 各是多少?答案:画出坐标系及受力情况,如图所示,已知两分力方向,作出平行四边形.由三角形关系得Fx=Fcos 30°=5 N, Fy=Fsin 30°=5 N.【知识梳理】
1.力的正交分解
(1)正交分解:把一个力分解为两个互相 的分力的方法.如图所示,Fx=
,Fy= .?
(2)优点:将矢量运算转化成 的标量运算.
2.力的分解的应用
当合力一定时,分力的 和 将随着分力间夹角的改变而改变.两个分力间的夹角越大,分力也就 .
(1)斧子劈圆木较 的力分解为较 的分力.
(2)石拱桥:将垂直向下的压力转化为两个 的分力.垂直Fcos θFsin θ坐标轴方向上大小方向越大小大斜向下【思考判断】
1.力的正交分解是指把一个力分解为水平和竖直两个方向互相垂直的分力的方法.( )
2.正交分解仅适用于矢量运算.( )
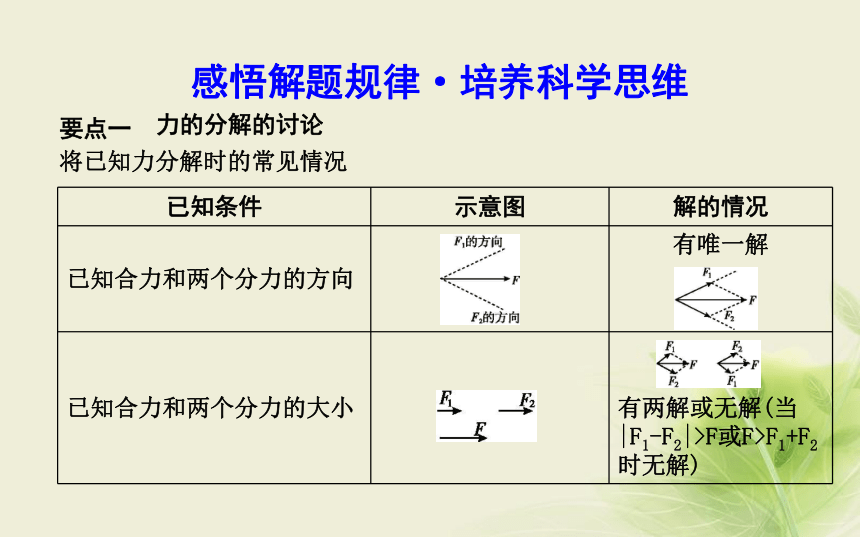
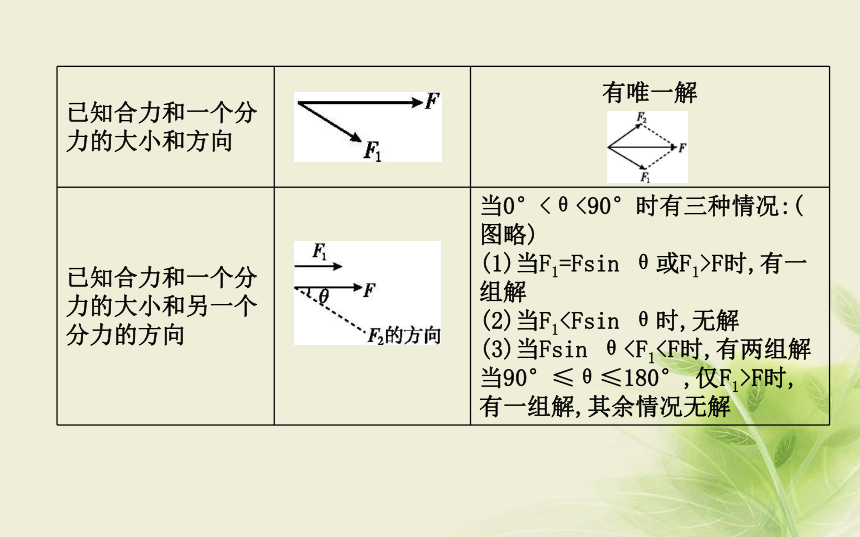
3.当物体受多个力作用时,常用正交分解法进行力的运算.( )×√√要点一感悟解题规律·培养科学思维力的分解的讨论将已知力分解时的常见情况?思路探究? 题目中若以F1,F,F2为边作完整三角形,则F2最小是多少?
答案:由几何关系知F2最小为Fsin 30°= .A 误区警示 力的分解的讨论
在已知合力的大小和方向以及一个分力的方向和另一个分力的大小时,将已知的合力分解需要注意无解、一解、双解的条件.本例中,合力与已知方向的分力间的夹角为锐角,并且F>F2= F>Fsin 30°,故有双解.(教师备用)
例1-1:(2016·济南模拟)(多选)已知合力的大小和方向求两个分力时,下列说法中正确的是( )
A.若已知两个分力的方向,分解是唯一的
B.若已知一个分力的大小和方向,分解是唯一的
C.若已知一个分力的大小及另一个分力的方向,分解是唯一的
D.此合力有可能分解成两个与合力等大的分力解析:已知两个分力的方向,或一个分力的大小和方向,根据平行四边形定则,只能画一个平行四边形,分解是唯一的,故选项A,B正确;如果将合力分解时两个分力夹角为120°且合力在其角平分线上,则两个分力与合力等大,故选项D正确;若已知一个分力F1的大小和另一个分力F2的方向,设F2与F夹角为θ,若F1A.此时两臂受到的压力大小均为2.0×105 N
B.此时千斤顶对汽车的支持力为4.0×105 N
C.若继续摇动把手,将汽车顶起,两臂受到的压力将减小
D.若继续摇动把手,将汽车顶起,两臂受到的压力将增大?思路探究?(1)汽车对千斤顶的压力产生的作用效果是什么?
答案:对千斤顶的两臂产生压力.
(2)千斤顶的压力与两臂的作用力间满足怎样的运算关系?
答案:平行四边形定则.AC要点二力的实际效果分解1.力的实际效果分解的思路实际问题 确定分力的方向 作出平行四边形 数学计算(求分力)2.常见实例分析【典例2】 (多选)物体所受重力为G,放在斜面上处于静止状态,斜面倾角为θ,将重力沿斜面方向和垂直斜面方向进行分解,如图所示,则由图可知( )
A. G1=Gcos θ
B. G2=Gcos θ
C.重力G的施力物体是地球
D.G1就是物体对斜面的压力 ?思路探究?由力的分解知识可知G1=Gcos θ, G2=Gsin θ,选项A正确, B错误;重力G的施力物体是地球,选项C正确;G1的大小等于物体对斜面的压力,选项D错误.AC规律方法 按实际效果分解的方法
在解决具体的物理问题时,一般都应该感受并确立力的实际作用效果,按力的效果确定好分力的方向,然后画出力的平行四边形,从而转化为根据已知边角关系求解的几何问题.(教师备用)
例2-1:如图所示,用两根承受的最大拉力相等、长度不等的细线AO,BO悬挂一个中空铁球,当在球内不断注入铁沙时,则下列说法正确的是( )
A.AO先被拉断 B.BO先被拉断
C.AO,BO同时被拉断 D.条件不足,无法判断解析:依据力的作用效果将重力分解,如图所示,据图可知FB>FA.又因为两绳承受能力相同,故当在球内不断注入铁沙时,BO绳先断,选项B正确.B ?针对训练2-1? 重力为G的光滑小球,分别被垂直于斜面的挡板和沿竖直方向放置的挡板挡住,静止在倾角为θ的斜面上,如图所示,求在甲、乙两种情况下,挡板对小球的支持力之比是多少?斜面对小球的支持力之比是多少?解析:小球的重力有两个作用效果,一个是使小球压紧挡板,另一个是使小球压紧斜面,所以可以把小球的重力按其效果分解为垂直于挡板方向的力G1和垂直于斜面向下的力G2,如图所示;G1与板对小球的支持力F是一对平衡力,即G1=F,G2与斜面对小球的支持力N是一对平衡力,即G2=N.对于图(a),由数学知识可得:G1a=Gsin θ,G2a=Gcos θ,则Fa=Gsin θ, Na=Gcos θ.答案:cos θ cos2θ要点三力的正交分解1.力的正交分解目的
正交分解,“分”的目的是为了更好地“合”.
2.方法步骤
(1)建立坐标系:以共点力的作用点为坐标原点,直角坐标系x轴和y轴的选择应使尽量多的力在坐标轴上.
(2)正交分解各力:将每一个不在坐标轴上的力分解到x轴和y轴上,并求出各分力的大小,如图所示.(3)分别求出x轴、y轴上各力的分力的合力,即
Fx合=F1x-F2x-F3x
Fy合=F1y+F2y-F3y
(4)求共点力的合力:合力大小F合= ,合力的方向与x轴的夹角为α,则tan α= .【典例3】 如图所示,力F1,F2,F3,F4在同一平面内构成共点力,其中F1=20 N, F2=20 N,F3=20 N,F4=20 N,各力之间的夹角在图中已标出.求这四个共点力的合力大小和方向.解析:以力F2的方向为x轴的正方向,建立如图所示的坐标系.
将F1,F3,F4向两坐标轴上分解得
方法总结 优先选用正交分解法的因素
正交分解法是为了更方便地求合力,所以选择正交分解法的题目有两个特点:(1)物体受力个数一般不少于三个;(2)建立坐标系后各力与坐标轴的夹角已知,且为常见的特殊角,如30°,45°,60°等.(教师备用)
例3-1:在同一平面内共点的四个力F1,F2,F3,F4的大小依次为 19 N,40 N, 30 N和15 N,方向如图所示,求它们的合力.解析:如图(甲)所示建立直角坐标系,把各个力分解到两个坐标轴上,设x轴和y轴上的合力分别为Fx和Fy,有Fx=F1+F2cos 37°-F3cos 37°=27 N,
Fy=F2sin 37°+F3sin 37°-F4=27 N,?针对训练3-1?如图所示,水平地面上有一质量为6 kg的物体,在与水平方向成60°角斜向上,大小为20 N的拉力F作用下匀速运动,求地面对物体的支持力和摩擦力大小.(g取10 m/s2) 解析:对物体进行受力分析,如图所示,物体受重力mg、支持力N、拉力F、摩擦力f.建立直角坐标系,对力进行正交分解得
y方向:N+Fsin 60°-mg=0
x方向:f-Fcos 60°=0
解得N=(60-10 )N,f=10 N.答案:(60-10 )N 10 N测评学习效果·演练当堂技法1.(多选)一个力F分解为两个力F1和F2,下列说法正确的是( )
A.F是物体实际受到的力
B.物体同时受到F1,F2和F三个力的作用
C.F1和F2的共同作用效果与F相同
D.F1,F2和F满足平行四边形定则ACD解析:在力的分解中,合力是实际存在的力,选项A正确;F1和F2是力F按效果分解的两个力,不是物体实际受到的力,选项B错误;F1和F2是力F的分力,F1和F2的共同作用效果与F相同,其关系满足平行四边形定则,故选项C,D正确.2.关于力的分解,下列叙述中不正确的是( )
A.8 N的力可以分解为两个8 N的力
B.8 N的力可以分解为两个4 N的力
C.8 N的力可以分解为13 N和6 N的两个分力
D.8 N的力可以分解为16 N和7 N的两个分力D 解析:根据合力和分力的大小关系可知,只要合力F合的大小与两分力F1,F2的大小关系满足|F1-F2|≤F合≤F1+F2均是可能的,16 N和7 N的两个力的合力范围为9 N≤F合≤23 N,故D不正确,比较可知,选项A,B,C均可.3.(多选)下列说法正确的是( )
A.力的分解是力的合成的逆运算
B.把一个力分解为两个分力,这两个分力共同作用的效果应当与该力作用的效果相同
C.力的合成和力的分解都遵循平行四边形定则
D.分力一定小于合力ABC解析:力的分解和力的合成都遵循平行四边形定则,互为逆运算,A,C正确;把一个力分解为两个分力,由合力和分力的定义可知,这两个分力共同作用的效果与该力作用的效果相同,B正确;由合力的取值范围|F1-F2|≤F≤F1+F2可知分力不一定小于合力,D错误.4.(2016·赣州高一检测)(多选)一个已知力F=10 N,把F分解为F1和F2两个分力,已知分力F1与F夹角为30°,则F2的大小( )
A.一定小于10 N B.可能等于10 N
C.可能大于10 N D.最小等于5 NBCD解析:由题意可知,当如图所示时,F2的大小最小,即最小值为F2min=F sin 30° =10×0.5 N=5 N;则F2的大小大于或等于5 N即可,故选项B,C,D正确,A错误.谢谢观赏!
1.知道分力和力的分解的概念.
2.理解力的分解是力的合成的逆运算,掌握分解力的方法.
3.能应用力的分解分析生产和生活中的相关问题.
科学思维与科学探究
1.体会等效替代的物理思想在探究自然规律中的作用,通过多举例、多演示,让学生将生活实际与物理概念相联系,通过实例分析掌握力的效果分解法和正交分解法.
2.结合三角形定则掌握图解法求分力、合力的技巧.
科学态度与责任
1.通过力的分解的学习,体会物理规律与生活的联系.
2.进一步渗透等效替代的物理思想.|教学重难点|教学重点
分力的求解.
教学难点
1.力的分解的讨论.
2.力的分解方法的应用.感悟解题规律探寻基本知识测评学习效果探寻基本知识·树立物理观念知识点一 分力 力的分解【情境导学】
为了行车方便和安全,高大的桥往往有很长的引桥.
问题:(1)在引桥上,汽车重力有什么作用效果?
(2)从力的分解的角度分析,引桥很长有什么好处?答案: (1)汽车重力的两个作用效果是垂直桥面向下使汽车压斜面和沿桥面向下使汽车下滑或阻碍汽车上行.
(2)高大的桥建造很长的引桥可以减小汽车重力沿斜面向下的分力,使行车更安全.【知识梳理】
1.分力:几个力共同作用的效果与一个力的作用效果相同,则这几个力叫那个力的分力.
2.力的分解
求一个已知力的 叫做力的分解.
3.力的分解法则
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的邻边就表示力F的两个分力F1,F2.
【思考判断】
1.一个力只能分解为一组分力.( )
2.力的分解遵循平行四边形定则.( )
3.某个分力的大小不可能大于合力.( )分力×√×知识点二力的正交分解与力的分解的应用【情境导学】已知竖直平面内有一个大小为10 N的力作用于O点,该力与x轴正方向之间的夹角为30°,与y轴正方向之间的夹角为60°,现将它分解到x轴和y轴方向上,则x轴和y轴上的分力Fx和Fy 各是多少?答案:画出坐标系及受力情况,如图所示,已知两分力方向,作出平行四边形.由三角形关系得Fx=Fcos 30°=5 N, Fy=Fsin 30°=5 N.【知识梳理】
1.力的正交分解
(1)正交分解:把一个力分解为两个互相 的分力的方法.如图所示,Fx=
,Fy= .?
(2)优点:将矢量运算转化成 的标量运算.
2.力的分解的应用
当合力一定时,分力的 和 将随着分力间夹角的改变而改变.两个分力间的夹角越大,分力也就 .
(1)斧子劈圆木较 的力分解为较 的分力.
(2)石拱桥:将垂直向下的压力转化为两个 的分力.垂直Fcos θFsin θ坐标轴方向上大小方向越大小大斜向下【思考判断】
1.力的正交分解是指把一个力分解为水平和竖直两个方向互相垂直的分力的方法.( )
2.正交分解仅适用于矢量运算.( )
3.当物体受多个力作用时,常用正交分解法进行力的运算.( )×√√要点一感悟解题规律·培养科学思维力的分解的讨论将已知力分解时的常见情况?思路探究? 题目中若以F1,F,F2为边作完整三角形,则F2最小是多少?
答案:由几何关系知F2最小为Fsin 30°= .A 误区警示 力的分解的讨论
在已知合力的大小和方向以及一个分力的方向和另一个分力的大小时,将已知的合力分解需要注意无解、一解、双解的条件.本例中,合力与已知方向的分力间的夹角为锐角,并且F>F2= F>Fsin 30°,故有双解.(教师备用)
例1-1:(2016·济南模拟)(多选)已知合力的大小和方向求两个分力时,下列说法中正确的是( )
A.若已知两个分力的方向,分解是唯一的
B.若已知一个分力的大小和方向,分解是唯一的
C.若已知一个分力的大小及另一个分力的方向,分解是唯一的
D.此合力有可能分解成两个与合力等大的分力解析:已知两个分力的方向,或一个分力的大小和方向,根据平行四边形定则,只能画一个平行四边形,分解是唯一的,故选项A,B正确;如果将合力分解时两个分力夹角为120°且合力在其角平分线上,则两个分力与合力等大,故选项D正确;若已知一个分力F1的大小和另一个分力F2的方向,设F2与F夹角为θ,若F1
B.此时千斤顶对汽车的支持力为4.0×105 N
C.若继续摇动把手,将汽车顶起,两臂受到的压力将减小
D.若继续摇动把手,将汽车顶起,两臂受到的压力将增大?思路探究?(1)汽车对千斤顶的压力产生的作用效果是什么?
答案:对千斤顶的两臂产生压力.
(2)千斤顶的压力与两臂的作用力间满足怎样的运算关系?
答案:平行四边形定则.AC要点二力的实际效果分解1.力的实际效果分解的思路实际问题 确定分力的方向 作出平行四边形 数学计算(求分力)2.常见实例分析【典例2】 (多选)物体所受重力为G,放在斜面上处于静止状态,斜面倾角为θ,将重力沿斜面方向和垂直斜面方向进行分解,如图所示,则由图可知( )
A. G1=Gcos θ
B. G2=Gcos θ
C.重力G的施力物体是地球
D.G1就是物体对斜面的压力 ?思路探究?由力的分解知识可知G1=Gcos θ, G2=Gsin θ,选项A正确, B错误;重力G的施力物体是地球,选项C正确;G1的大小等于物体对斜面的压力,选项D错误.AC规律方法 按实际效果分解的方法
在解决具体的物理问题时,一般都应该感受并确立力的实际作用效果,按力的效果确定好分力的方向,然后画出力的平行四边形,从而转化为根据已知边角关系求解的几何问题.(教师备用)
例2-1:如图所示,用两根承受的最大拉力相等、长度不等的细线AO,BO悬挂一个中空铁球,当在球内不断注入铁沙时,则下列说法正确的是( )
A.AO先被拉断 B.BO先被拉断
C.AO,BO同时被拉断 D.条件不足,无法判断解析:依据力的作用效果将重力分解,如图所示,据图可知FB>FA.又因为两绳承受能力相同,故当在球内不断注入铁沙时,BO绳先断,选项B正确.B ?针对训练2-1? 重力为G的光滑小球,分别被垂直于斜面的挡板和沿竖直方向放置的挡板挡住,静止在倾角为θ的斜面上,如图所示,求在甲、乙两种情况下,挡板对小球的支持力之比是多少?斜面对小球的支持力之比是多少?解析:小球的重力有两个作用效果,一个是使小球压紧挡板,另一个是使小球压紧斜面,所以可以把小球的重力按其效果分解为垂直于挡板方向的力G1和垂直于斜面向下的力G2,如图所示;G1与板对小球的支持力F是一对平衡力,即G1=F,G2与斜面对小球的支持力N是一对平衡力,即G2=N.对于图(a),由数学知识可得:G1a=Gsin θ,G2a=Gcos θ,则Fa=Gsin θ, Na=Gcos θ.答案:cos θ cos2θ要点三力的正交分解1.力的正交分解目的
正交分解,“分”的目的是为了更好地“合”.
2.方法步骤
(1)建立坐标系:以共点力的作用点为坐标原点,直角坐标系x轴和y轴的选择应使尽量多的力在坐标轴上.
(2)正交分解各力:将每一个不在坐标轴上的力分解到x轴和y轴上,并求出各分力的大小,如图所示.(3)分别求出x轴、y轴上各力的分力的合力,即
Fx合=F1x-F2x-F3x
Fy合=F1y+F2y-F3y
(4)求共点力的合力:合力大小F合= ,合力的方向与x轴的夹角为α,则tan α= .【典例3】 如图所示,力F1,F2,F3,F4在同一平面内构成共点力,其中F1=20 N, F2=20 N,F3=20 N,F4=20 N,各力之间的夹角在图中已标出.求这四个共点力的合力大小和方向.解析:以力F2的方向为x轴的正方向,建立如图所示的坐标系.
将F1,F3,F4向两坐标轴上分解得
方法总结 优先选用正交分解法的因素
正交分解法是为了更方便地求合力,所以选择正交分解法的题目有两个特点:(1)物体受力个数一般不少于三个;(2)建立坐标系后各力与坐标轴的夹角已知,且为常见的特殊角,如30°,45°,60°等.(教师备用)
例3-1:在同一平面内共点的四个力F1,F2,F3,F4的大小依次为 19 N,40 N, 30 N和15 N,方向如图所示,求它们的合力.解析:如图(甲)所示建立直角坐标系,把各个力分解到两个坐标轴上,设x轴和y轴上的合力分别为Fx和Fy,有Fx=F1+F2cos 37°-F3cos 37°=27 N,
Fy=F2sin 37°+F3sin 37°-F4=27 N,?针对训练3-1?如图所示,水平地面上有一质量为6 kg的物体,在与水平方向成60°角斜向上,大小为20 N的拉力F作用下匀速运动,求地面对物体的支持力和摩擦力大小.(g取10 m/s2) 解析:对物体进行受力分析,如图所示,物体受重力mg、支持力N、拉力F、摩擦力f.建立直角坐标系,对力进行正交分解得
y方向:N+Fsin 60°-mg=0
x方向:f-Fcos 60°=0
解得N=(60-10 )N,f=10 N.答案:(60-10 )N 10 N测评学习效果·演练当堂技法1.(多选)一个力F分解为两个力F1和F2,下列说法正确的是( )
A.F是物体实际受到的力
B.物体同时受到F1,F2和F三个力的作用
C.F1和F2的共同作用效果与F相同
D.F1,F2和F满足平行四边形定则ACD解析:在力的分解中,合力是实际存在的力,选项A正确;F1和F2是力F按效果分解的两个力,不是物体实际受到的力,选项B错误;F1和F2是力F的分力,F1和F2的共同作用效果与F相同,其关系满足平行四边形定则,故选项C,D正确.2.关于力的分解,下列叙述中不正确的是( )
A.8 N的力可以分解为两个8 N的力
B.8 N的力可以分解为两个4 N的力
C.8 N的力可以分解为13 N和6 N的两个分力
D.8 N的力可以分解为16 N和7 N的两个分力D 解析:根据合力和分力的大小关系可知,只要合力F合的大小与两分力F1,F2的大小关系满足|F1-F2|≤F合≤F1+F2均是可能的,16 N和7 N的两个力的合力范围为9 N≤F合≤23 N,故D不正确,比较可知,选项A,B,C均可.3.(多选)下列说法正确的是( )
A.力的分解是力的合成的逆运算
B.把一个力分解为两个分力,这两个分力共同作用的效果应当与该力作用的效果相同
C.力的合成和力的分解都遵循平行四边形定则
D.分力一定小于合力ABC解析:力的分解和力的合成都遵循平行四边形定则,互为逆运算,A,C正确;把一个力分解为两个分力,由合力和分力的定义可知,这两个分力共同作用的效果与该力作用的效果相同,B正确;由合力的取值范围|F1-F2|≤F≤F1+F2可知分力不一定小于合力,D错误.4.(2016·赣州高一检测)(多选)一个已知力F=10 N,把F分解为F1和F2两个分力,已知分力F1与F夹角为30°,则F2的大小( )
A.一定小于10 N B.可能等于10 N
C.可能大于10 N D.最小等于5 NBCD解析:由题意可知,当如图所示时,F2的大小最小,即最小值为F2min=F sin 30° =10×0.5 N=5 N;则F2的大小大于或等于5 N即可,故选项B,C,D正确,A错误.谢谢观赏!
同课章节目录
- 第1章 绪论
- 物理学与自然规律
- 物理学与社会发展
- 怎样学习物理学
- 高中物理教材特点
- 第2章 运动的描述
- 导入 认识运动
- 第1节 运动、空间和时间
- 第2节 质点和位移
- 第3节 速度和加速度
- 第3章 匀变速直线运动的研究
- 导入 速度的变化
- 第1节 匀变速直线运动的规律
- 第2节 匀变速直线运动的实验探究
- 第3节 匀变速直线运动实例-自由落体运动
- 第4章 相互作用
- 导入 奇特的力现象
- 第1节 重力与重心
- 第2节 形变与弹力
- 第3节 摩擦力
- 第5章 力与平衡
- 导入 感悟平衡之美
- 第1节 力的合成
- 第2节 力的分解
- 第3节 力的平衡
- 第4节 平衡条件的应用
- 第6章 力与运动
- 导入 跨越时空的对话
- 第1节 牛顿第一定律
- 第2节 牛顿第二定律
- 第3节 牛顿第三定律
- 第4节 超重与失重
- 本章复习与测试
