2018学年高中物理第2章气体等容变化和等压变化学案教科版选修3_3
文档属性
| 名称 | 2018学年高中物理第2章气体等容变化和等压变化学案教科版选修3_3 |

|
|
| 格式 | zip | ||
| 文件大小 | 496.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-09-05 08:50:40 | ||
图片预览




文档简介
等容变化和等压变化
【学习目标】
1.知道什么是等容变化和等压变化;
2.知道查理定律内容及表达式;
3.知道盖一吕萨克定律内容及表达式;
4.知道图象和图象及物理意义;
5.知道热力学温标;
6.熟练利用查理定律及图象和图象分析解决相关问题.
【要点梳理】
要点一、气体的等容变化 查理定律
1.气体的等容变化
气体的等容变化:气体体积保持不变的情况下所发生的状态变化叫等容变化.
2.等容变化规律
(1)实验条件:
气体质量一定;
气体体积不变.
(2)实验过程:
在室温下封闭一定质量的气体在烧瓶中,记下气体的体积和压强.
把烧瓶放入冰水混合物的容器里。记下这时温度为,调整压强计保持气体体积不变,记下压强.如图所示.
把烧瓶放在温度为的温水中,调整压强计保持气体体积不变,记下压强.
(3)实验结论:一定质量的某种气体,在体积不变的条件下,气体的压强随温度升高而增大,随温度降低而减小.
3.摄氏温标下的查理定律
(1)定律:一定质量的某种气体,在体积不变的条件下,气体温度每升高(或降低),增加(或减小)的压强等于气体在时压强的.这条规律叫做查理定律.
(2)公式:或。
其中是温度为时的压强,是时的压强.
(3)等容曲线,如图所示.
要点诠释:图象:一定质量的某种气体,在等容过程中,压强与摄氏温度是一次函数关系,不是简单的正比例关系,等容线是一条延长线通过横轴的倾斜直线,且斜率越大,体积越小.图象纵轴的截距是气体在时的压强.
4.热力学温标下的查理定律
(1)定律:一定质量的气体,在体积不变的条件下,气体的压强跟热力学温度成正比.
(2)公式:,或.
(3)等容曲线,如图所示.
要点诠释:图象:一定质量的某种气体,在等容过程中,气体的压强和热力学温度的图线是过原点的倾斜直线,如图所示,且,即体积越大,斜率越小.
5.查理定律的微观解释
一定质量的气体,说明气体总分子数不变;气体体积不变,则单位体积内的分子数不变;当气体温度升高时,说明分子的平均速率增大,则单位时间内,分子跟器壁单位面积碰撞的次数增多,且每次碰撞器壁产生的平均冲力增大,因此气体压强将增大.
6.查理定律的适用条件
对实际气体,温度不太低(与室温比较),压强不太大(与大气压相比)的情况.
要点二、气体的等压变化,盖一吕萨克定律
1.气体的等压变化
气体在压强不变的情况下所发生的状态变化叫做等压变化.
2.盖一吕萨克定律
(1)一定质量的某种气体,在压强不变的情况下,温度每升高(或降低),增加(或减少)的体积等于它在时体积的,这就是盖一吕萨克定律.其数学表达式为
或.
(2)采用热力学温标时,盖一吕萨克定律可表述为:一定质量的某种气体,在压强不变的情况下,它的体积跟热力学温度成正比.其数学表达式为
或。
(3)适用条件:对于实际气体,温度不太低(与室温比较),压强不太大(与大气压相比)的情况.
3.和图象
(1)图象:一定质量的某种气体,在等压过程中,气体的体积和热力学温度的图线是过原点的倾斜直线,如图甲所示,且,即压强越大,斜率越小.
(2)图象:一定质量的某种气体,在等压过程中,体积与摄氏温度是一次线性函数,不是简单的正比例关系,如图乙所示,图象纵轴的截距是气体在时的体积,等压线是一条延长线通过横轴上的倾斜直线,且斜率越大,压强越小.
要点三、两个重要的推论
(1)一定质量的某种气体,从初状态()开始,发生一个等容变化过程,其压强的变化量与温度的变化量间的关系为
。
这是查理定律的分比形式.
(2)一定质量的某种气体从初状态()开始发生等压变化,其体积的改变量与温度变化量之间的关系是
。
这是盖一吕萨克定律的分比形式.
要点四、利用查理定律和盖一吕萨克定律解题的一般步骤、汞柱移动问题的分析方法
1.利用查理定律和盖一吕萨克定律解题的一般步骤
(1)确定研究对象,即某被封闭气体.
(2)分析状态变化过程,明确初、末状态,确认在状态变化过程中气体的质量和体积保持不变.
(3)分别找出初、末两状态的温度、压强或温度、体积.
(4)根据查理定律和盖一吕萨克定律列方程求解.
(5)分析所求结果是否合理.
2.汞柱移动问题的分析方法
(1)假设法
用液柱或活塞隔开两部分气体,当气体温度变化时,液柱或活塞是否移动?如何移动?此类问题的特点是:气体的状态参量都发生了变化,直接判断液柱或活塞的移动方向比较困难,通常先进行气体状态的假设,然后应用查理定律可以简单地求解.其一般思路为:
①先假设液柱或活塞不发生移动,两部分气体均做等容变化.
②对两部分气体分别应用查理定律的分比形式,求出每部分气体压强的变化量,并加以比较.
③如果液柱两端的横截面积相等,则若均大于零,意味着两部分气体的压强均增大,则液柱向值较小的一方移动;若均小于零,意味着两部分气体的压强均减小,则液柱向压强减小量较大的一方(即||较大的一方)移动;若卸相等,则液柱不移动.
④如果液柱两端的横截面积不相等,则应考虑液柱两端的受力变化(),若均大于零,则液柱向较小的一方移动;若均小于零,则液柱向||值较大的一方移动;若相等,则液柱不移动.
⑤要判断活塞的移动方向,则需要选择好研究对象,进行受力分析,综合应用查理定律和力学规律进行推理和判断.
(2)极限法
所谓极限法就是将问题推向极端.如在讨论压强大小变化时,将变化较大的压强推向无穷大,而将变化较小的压强推向零.这样使复杂的问题变得简单明了.
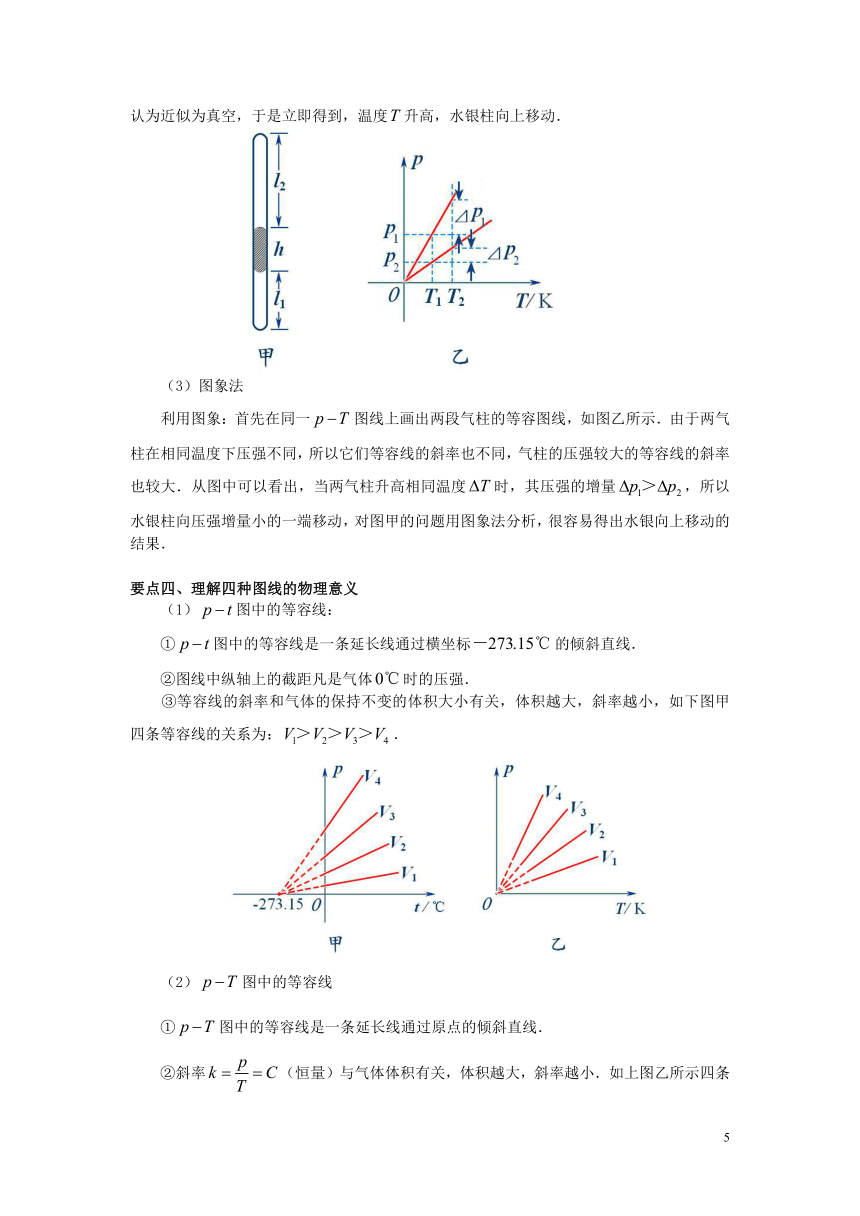
如图甲所示,两端封闭、粗细均匀、竖直放置的玻璃管内有一段长为的水银柱,将管内气体分为两部分.已知,若使两部分气体同时升高相同的温度,管内水银柱将如何运动?(设原来温度相同)
根据极限法:由于管上段气柱压强较下段气柱压强小,设想,即管上部认为近似为真空,于是立即得到,温度升高,水银柱向上移动.
(3)图象法
利用图象:首先在同一图线上画出两段气柱的等容图线,如图乙所示.由于两气柱在相同温度下压强不同,所以它们等容线的斜率也不同,气柱的压强较大的等容线的斜率也较大.从图中可以看出,当两气柱升高相同温度时,其压强的增量,所以水银柱向压强增量小的一端移动,对图甲的问题用图象法分析,很容易得出水银向上移动的结果.
要点四、理解四种图线的物理意义
(1)图中的等容线:
①图中的等容线是一条延长线通过横坐标的倾斜直线.
②图线中纵轴上的截距凡是气体时的压强.
③等容线的斜率和气体的保持不变的体积大小有关,体积越大,斜率越小,如下图甲四条等容线的关系为:.
(2)图中的等容线
①图中的等容线是一条延长线通过原点的倾斜直线.
②斜率(恒量)与气体体积有关,体积越大,斜率越小.如上图乙所示四条等容线的关系为:.
(3)下图甲所示为图中的等压线,这是一条延长线过的倾斜直线,纵轴上截距表示气体在时的体积.等压线的斜率大小取决于压强的大小,压强越大,斜率越小.图中四条等压线的关系为:.
(4)如上图乙所示为图中的等压线,这是一条延长线通过原点的倾斜直线,直线斜率,斜率越大,恒量越大,压强越小.在图中给出的四条等压线的关系为:.
要点五、知识归纳总结
1.知识网络
2.知识梳理
等容变化过程中查理定律和等压变化过程中盖一吕萨克定律是在实验基础上总结出来的规律,确定一个量不变的情况下另外两个量的比例关系.查理定律中,气体的压强和热力学温度成正比;盖一吕萨克定律中,气体的体积和热力学温度成正比.
【典型例题】
类型一、气体的等容变化 查理定律
例1.密封在容积不变的容器中的气体,当温度降低时( ).
A.压强减小,密度减小 B.压强减小,密度增大
C.压强不变,密度减小 D.压强减小,密度不变
【思路点拨】属于等容变化,运用查理定律。
【答案】 D
【解析】 本题考查的知识点是气体的等容变化.由查理定律得,当体积不变时,热力学温度与压强成正比,因此温度降低时,压强减小.因为质量和体积都不发生变化,因此密度不变.故正确答案为D.
【总结升华】抓住体积不变这一特点,再利用即查理定律作出判断。
举一反三:
【变式1】起飞前高空试验火箭仪器舱内,气压压强,温度.当火箭竖直向上加速飞行()时,仪器舱内水银气压计示数为.已知舱是密封的,可以判定此时舱内的温度是________.
【答案】
【解析】加速前后,仪器舱内气体做的是等容变化,可以用查理定律求加速时舱内温度.
取舱内气体为研究对象,由查理定律得
. ①
取气压计内高出液面的水银柱为研究对象,由牛顿第二定律得
. ②
又
. ③
由①②③得,.
【总结升华】挖掘出舱内气体做等容变化是解题的关键,其次要灵活运用液体压强公式。
【变式2】电灯泡内充有氮、氩混合气体,如果要使灯泡内的混合气体在时的压强不超过一个大气压,则在的室温下充气,电灯泡内气体压强至多能充到多少?
【答案】见解析
【解析】忽略灯泡容积的变化,气体为等容变化,找出气体的初、末状态,运用查理定律的两种表述皆可求解.
设时气体的压强为,时气体的压强为,时气体的压强为.由查理定律
可得
,.
所以
.
故
.
【总结升华】 ①一定质量的某种气体在体积不变的情况下,压强跟热力学温度成正比,即(常数)或。
②在查理定律的第一种表述中,气体的温度是热力学温度,而在第二种表述中则是摄氏温度,而且式中是时气体的压强,并非气体初状态的压强。
例2.如图所示是一定质量的理想气体的三种升温过程,那么,以下四种解释中,哪些是正确的?( ).
A.的过程气体体积增加 B.的过程气体体积不变
C.的过程气体体积增加 D.的过程气体体积减小
【答案】A、B
【解析】在图上的等容线的延长线是过原点的直线,且体积越大,直线的斜率越小.由此可见,状态对应体积最小,状态对应体积最大.所以选项A、B是正确的.
【总结升华】一定质量的气体,等容过程中图线是过原点的倾斜直线,其斜率越大,体积越小。
举一反三:
【变式】一定质量的理想气体的图象,如图所示,在气体由状态变化到状态的过程中,体积怎样变化?( ).
A.一定不变 B.一定减小 C.一定增加 D.不能判定
【答案】D
【解析】图中横坐标表示的是摄氏温度.若的延长线与轴相交在,则表示到过程中体积是不变的.但是,由图中无法作出这样的判定.所以,应选D.
【总结升华】一定质量的气体,等容过程中图线是一次线性函数,但并不过原点,其反向延长线与横轴的交点为。
类型二、气体的等压变化,盖一吕萨克定律
例3.如图,竖直放置、开口向上的试管内用水银封闭一段理想气体,若大气压强不变,管内气体( ).
A.温度升高,则体积增大 B.温度升高,则体积减小
C.温度降低,则压强增大 D.温度降低,则压强减小
【思路点拨】属于等压变化.运用盖一吕萨克定律。
【答案】A
【解析】由盖-吕萨克定律知:
增大,则增大,减小,则减小,故A正确。
【总结升华】抓住等压变化时恒量进行分析解题,就一定能作出判断。
举一反三:
【变式】一定质量的气体,如果保持它的压强不变,降低温度,使它的体积为时体积的倍,则此时气体的温度为( ).
A. B.
C. D.
【答案】C
【解析】根据盖一吕萨克定律,在压强不变的条件下,即根据题意,整理后得.
例4.一个开着窗户的房间,温度为时室内空气质量为,当温度升高到时,室内空气的质量为。
【答案】
【解析】应用盖一吕萨克定律,以跑到室外的气体与室内的气体整体为研究对象,设原来体积为,温度升高后体积为,已知,,根据盖—吕萨克定律:
得
.
因温度升高后留在室内的气体体积仍为,占总体积的比例为
.
∴.
【总结升华】解答此类问题关键是将变质量问题从整体角度分析,转化为一定质量的问题,再由等压变化规律求解。
类型三、汞柱移动问题
例5.如图所示,两容器容积相等,用粗细均匀的细玻璃管相连,两容器内装有不同气体,细管中央有一段水银柱,在两边气体作用下保持平衡时,中气体的温度为,中气体温度为,如果将它们的温度都降低,则水银柱将( ).
A.向移动 B.向移动 C.不动 D.不能确定
【思路点拨】假设液柱不动,假设液柱不动,根据查理定律进行分析。
【答案】A
【解析】由,可知.
∴部分气体压强减小得多,左移.
【总结升华】分析解答此类问题的方法是:首先假设液柱不动,假设液柱不动,则两部分气体做等容变化,根据查理定律的分比形式确定,各自压强的变化,从而判定液柱的移动方向。
举一反三:
【变式】如图所示,容器和分别盛有氢气和氧气,用一段竖直细玻璃管连通,管内有一段水银柱将两种气体隔开.当氢气的温度和氧气温度相等时,水银柱保持静止,则当两气体均降低相同的温度时,水银柱将怎样移动?
【答案】向下移动
【解析】假设水银柱不动,由公式分别求出两部分气体的卸值,加以比较进行判断.
对两部分气体:,.
因(对图分析),故,水银柱向容器一方(向下)移动.
【总结升华】判断液柱移动的方向往往采用假设法,假设液柱不动,然后由查理定律的分比形式比较压强的变化,从而判断出液体移动的方向。
例6.如图所示,一端封闭的粗细均匀的玻璃管,开口向上竖直放置,管中有两段水银柱封闭了两段空气柱,开始时,现将玻璃管缓慢地均匀加热,则下述说法中正确的是( ).
A.加热过程中,始终保持
B.加热后,
C.加热后,
D.条件不足,无法确定
【答案】A
【解析】在整个加热过程中,上段气柱的压强始终保持为不变,下段气柱的压强始终为不变,所以整个过程为等压变化,根据盖一吕萨克定律:
得.
得.
∴,即。
【总结升华】解答本题关键是抓住在温度变化时,压强不变,分别对和列方程求解。
举一反三:
【变式】如图所示的玻璃管ABCDE,CD部分水平,其余部分竖直(B端弯曲部分长度可忽略),玻璃管截面半径相比其长度可忽略,CD内有一段水银柱,初始时数据如图,环境温度是300K,大气压是75cmHg。现保持CD水平,将玻璃管A端缓慢竖直向下插入大水银槽中,当水平段水银柱刚好全部进入DE竖直管内时,保持玻璃管静止不动。问:
(1)玻璃管A端插入大水银槽中的深度是多少?(即水银面到管口A的竖直距离)?
(2)当管内气体温度缓慢降低到多少K时,DE中的水银柱刚好回到CD水平管中?
【答案】(1)25cm;(2)T3=262.5K
【解析】(1)以玻璃管内气体为研究对象,设玻璃管横截面积为S,
p1=p0=75cmHg,V1=(140+15+5)S=160S,p2=p0+h1=75+5=80cmHg,
由玻意耳定律可得:p1V1=p2V2,即:75×160S=80×L2S,
L2=150cm,
h=160+10–150+5=25cm; (2)T1=300K,V1=160S,V3=(140+15+10–25)S=140S,
由盖吕萨克定律得:,即,
解得T3=262.5K。
类型四、理解图线的物理意义
例7.一定质量的某种气体自状态经状态变化到状态,这一过程在图上表示如图所示,则( ).
A.在过程中,气体的压强不断变大
B.在过程中,气体的压强不断变小
C.在状态时,气体的压强最大
D.在状态时,气体的压强最大
【思路点拨】用这两个状态到原点连线的斜率大小来判断。
【答案】A、D
【解析】气体在过程中发生等温变化,由可知,体积减小,压强增大,故A正确.在变化过程中,气体的体积不发生变化,即为等容变化,由可知,温度升高,压强增大,故B错误.综上所述,在过程中气体的压强始终增大,所以气体在状态时的压强最大,故C错误,D正确.
【总结升华】在图象中,比较两个状态的压强大小,可以用这两个状态到原点连线的斜率大小来判断,斜率越大、压强越小,斜率越小、压强越大。
举一反三:
【变式】图甲是一定质量的气体由状态经过状态变为状态的图象.已知气体在状态时的压强是.
(1)说出过程中压强变化的情形,并根据图象提供的信息,计算图中的温度值.
(2)请在图乙坐标系中,作出由状态经过状态变为状态的图象,并在图线相应位置上标出字母,如果需要计算才能确定有关坐标值,请写出计算过程.
【答案】(1) (2)见解析
【解析】(1)由图甲可以看出,与的连线的延长线过原点,所以是一个等压变化,即.
根据盖一吕萨克定律可知:
,
∴.
(2)由图甲可知,由是等容变化,根据查理定律得:
.
∴.
则可画出由状态的图象如下图所示。
【总结升华】熟练运用盖—吕萨克定律和查理定律,理解图象和图象的物理意义是解题的关键。
等容变化和等压变化
【学习目标】
1.知道什么是等容变化和等压变化;
2.知道查理定律内容及表达式;
3.知道盖一吕萨克定律内容及表达式;
4.知道图象和图象及物理意义;
5.知道热力学温标;
6.熟练利用查理定律及图象和图象分析解决相关问题.
【要点梳理】
要点一、气体的等容变化 查理定律
1.气体的等容变化
气体的等容变化:气体体积保持不变的情况下所发生的状态变化叫等容变化.
2.等容变化规律
(1)实验条件:
气体质量一定;
气体体积不变.
(2)实验过程:
在室温下封闭一定质量的气体在烧瓶中,记下气体的体积和压强.
把烧瓶放入冰水混合物的容器里。记下这时温度为,调整压强计保持气体体积不变,记下压强.如图所示.
把烧瓶放在温度为的温水中,调整压强计保持气体体积不变,记下压强.
(3)实验结论:一定质量的某种气体,在体积不变的条件下,气体的压强随温度升高而增大,随温度降低而减小.
3.摄氏温标下的查理定律
(1)定律:一定质量的某种气体,在体积不变的条件下,气体温度每升高(或降低),增加(或减小)的压强等于气体在时压强的.这条规律叫做查理定律.
(2)公式:或。
其中是温度为时的压强,是时的压强.
(3)等容曲线,如图所示.
要点诠释:图象:一定质量的某种气体,在等容过程中,压强与摄氏温度是一次函数关系,不是简单的正比例关系,等容线是一条延长线通过横轴的倾斜直线,且斜率越大,体积越小.图象纵轴的截距是气体在时的压强.
4.热力学温标下的查理定律
(1)定律:一定质量的气体,在体积不变的条件下,气体的压强跟热力学温度成正比.
(2)公式:,或.
(3)等容曲线,如图所示.
要点诠释:图象:一定质量的某种气体,在等容过程中,气体的压强和热力学温度的图线是过原点的倾斜直线,如图所示,且,即体积越大,斜率越小.
5.查理定律的微观解释
一定质量的气体,说明气体总分子数不变;气体体积不变,则单位体积内的分子数不变;当气体温度升高时,说明分子的平均速率增大,则单位时间内,分子跟器壁单位面积碰撞的次数增多,且每次碰撞器壁产生的平均冲力增大,因此气体压强将增大.
6.查理定律的适用条件
对实际气体,温度不太低(与室温比较),压强不太大(与大气压相比)的情况.
要点二、气体的等压变化,盖一吕萨克定律
1.气体的等压变化
气体在压强不变的情况下所发生的状态变化叫做等压变化.
2.盖一吕萨克定律
(1)一定质量的某种气体,在压强不变的情况下,温度每升高(或降低),增加(或减少)的体积等于它在时体积的,这就是盖一吕萨克定律.其数学表达式为
或.
(2)采用热力学温标时,盖一吕萨克定律可表述为:一定质量的某种气体,在压强不变的情况下,它的体积跟热力学温度成正比.其数学表达式为
或。
(3)适用条件:对于实际气体,温度不太低(与室温比较),压强不太大(与大气压相比)的情况.
3.和图象
(1)图象:一定质量的某种气体,在等压过程中,气体的体积和热力学温度的图线是过原点的倾斜直线,如图甲所示,且,即压强越大,斜率越小.
(2)图象:一定质量的某种气体,在等压过程中,体积与摄氏温度是一次线性函数,不是简单的正比例关系,如图乙所示,图象纵轴的截距是气体在时的体积,等压线是一条延长线通过横轴上的倾斜直线,且斜率越大,压强越小.
要点三、两个重要的推论
(1)一定质量的某种气体,从初状态()开始,发生一个等容变化过程,其压强的变化量与温度的变化量间的关系为
。
这是查理定律的分比形式.
(2)一定质量的某种气体从初状态()开始发生等压变化,其体积的改变量与温度变化量之间的关系是
。
这是盖一吕萨克定律的分比形式.
要点四、利用查理定律和盖一吕萨克定律解题的一般步骤、汞柱移动问题的分析方法
1.利用查理定律和盖一吕萨克定律解题的一般步骤
(1)确定研究对象,即某被封闭气体.
(2)分析状态变化过程,明确初、末状态,确认在状态变化过程中气体的质量和体积保持不变.
(3)分别找出初、末两状态的温度、压强或温度、体积.
(4)根据查理定律和盖一吕萨克定律列方程求解.
(5)分析所求结果是否合理.
2.汞柱移动问题的分析方法
(1)假设法
用液柱或活塞隔开两部分气体,当气体温度变化时,液柱或活塞是否移动?如何移动?此类问题的特点是:气体的状态参量都发生了变化,直接判断液柱或活塞的移动方向比较困难,通常先进行气体状态的假设,然后应用查理定律可以简单地求解.其一般思路为:
①先假设液柱或活塞不发生移动,两部分气体均做等容变化.
②对两部分气体分别应用查理定律的分比形式,求出每部分气体压强的变化量,并加以比较.
③如果液柱两端的横截面积相等,则若均大于零,意味着两部分气体的压强均增大,则液柱向值较小的一方移动;若均小于零,意味着两部分气体的压强均减小,则液柱向压强减小量较大的一方(即||较大的一方)移动;若卸相等,则液柱不移动.
④如果液柱两端的横截面积不相等,则应考虑液柱两端的受力变化(),若均大于零,则液柱向较小的一方移动;若均小于零,则液柱向||值较大的一方移动;若相等,则液柱不移动.
⑤要判断活塞的移动方向,则需要选择好研究对象,进行受力分析,综合应用查理定律和力学规律进行推理和判断.
(2)极限法
所谓极限法就是将问题推向极端.如在讨论压强大小变化时,将变化较大的压强推向无穷大,而将变化较小的压强推向零.这样使复杂的问题变得简单明了.
如图甲所示,两端封闭、粗细均匀、竖直放置的玻璃管内有一段长为的水银柱,将管内气体分为两部分.已知,若使两部分气体同时升高相同的温度,管内水银柱将如何运动?(设原来温度相同)
根据极限法:由于管上段气柱压强较下段气柱压强小,设想,即管上部认为近似为真空,于是立即得到,温度升高,水银柱向上移动.
(3)图象法
利用图象:首先在同一图线上画出两段气柱的等容图线,如图乙所示.由于两气柱在相同温度下压强不同,所以它们等容线的斜率也不同,气柱的压强较大的等容线的斜率也较大.从图中可以看出,当两气柱升高相同温度时,其压强的增量,所以水银柱向压强增量小的一端移动,对图甲的问题用图象法分析,很容易得出水银向上移动的结果.
要点四、理解四种图线的物理意义
(1)图中的等容线:
①图中的等容线是一条延长线通过横坐标的倾斜直线.
②图线中纵轴上的截距凡是气体时的压强.
③等容线的斜率和气体的保持不变的体积大小有关,体积越大,斜率越小,如下图甲四条等容线的关系为:.
(2)图中的等容线
①图中的等容线是一条延长线通过原点的倾斜直线.
②斜率(恒量)与气体体积有关,体积越大,斜率越小.如上图乙所示四条等容线的关系为:.
(3)下图甲所示为图中的等压线,这是一条延长线过的倾斜直线,纵轴上截距表示气体在时的体积.等压线的斜率大小取决于压强的大小,压强越大,斜率越小.图中四条等压线的关系为:.
(4)如上图乙所示为图中的等压线,这是一条延长线通过原点的倾斜直线,直线斜率,斜率越大,恒量越大,压强越小.在图中给出的四条等压线的关系为:.
要点五、知识归纳总结
1.知识网络
2.知识梳理
等容变化过程中查理定律和等压变化过程中盖一吕萨克定律是在实验基础上总结出来的规律,确定一个量不变的情况下另外两个量的比例关系.查理定律中,气体的压强和热力学温度成正比;盖一吕萨克定律中,气体的体积和热力学温度成正比.
【典型例题】
类型一、气体的等容变化 查理定律
例1.密封在容积不变的容器中的气体,当温度降低时( ).
A.压强减小,密度减小 B.压强减小,密度增大
C.压强不变,密度减小 D.压强减小,密度不变
【思路点拨】属于等容变化,运用查理定律。
【答案】 D
【解析】 本题考查的知识点是气体的等容变化.由查理定律得,当体积不变时,热力学温度与压强成正比,因此温度降低时,压强减小.因为质量和体积都不发生变化,因此密度不变.故正确答案为D.
【总结升华】抓住体积不变这一特点,再利用即查理定律作出判断。
举一反三:
【变式1】起飞前高空试验火箭仪器舱内,气压压强,温度.当火箭竖直向上加速飞行()时,仪器舱内水银气压计示数为.已知舱是密封的,可以判定此时舱内的温度是________.
【答案】
【解析】加速前后,仪器舱内气体做的是等容变化,可以用查理定律求加速时舱内温度.
取舱内气体为研究对象,由查理定律得
. ①
取气压计内高出液面的水银柱为研究对象,由牛顿第二定律得
. ②
又
. ③
由①②③得,.
【总结升华】挖掘出舱内气体做等容变化是解题的关键,其次要灵活运用液体压强公式。
【变式2】电灯泡内充有氮、氩混合气体,如果要使灯泡内的混合气体在时的压强不超过一个大气压,则在的室温下充气,电灯泡内气体压强至多能充到多少?
【答案】见解析
【解析】忽略灯泡容积的变化,气体为等容变化,找出气体的初、末状态,运用查理定律的两种表述皆可求解.
设时气体的压强为,时气体的压强为,时气体的压强为.由查理定律
可得
,.
所以
.
故
.
【总结升华】 ①一定质量的某种气体在体积不变的情况下,压强跟热力学温度成正比,即(常数)或。
②在查理定律的第一种表述中,气体的温度是热力学温度,而在第二种表述中则是摄氏温度,而且式中是时气体的压强,并非气体初状态的压强。
例2.如图所示是一定质量的理想气体的三种升温过程,那么,以下四种解释中,哪些是正确的?( ).
A.的过程气体体积增加 B.的过程气体体积不变
C.的过程气体体积增加 D.的过程气体体积减小
【答案】A、B
【解析】在图上的等容线的延长线是过原点的直线,且体积越大,直线的斜率越小.由此可见,状态对应体积最小,状态对应体积最大.所以选项A、B是正确的.
【总结升华】一定质量的气体,等容过程中图线是过原点的倾斜直线,其斜率越大,体积越小。
举一反三:
【变式】一定质量的理想气体的图象,如图所示,在气体由状态变化到状态的过程中,体积怎样变化?( ).
A.一定不变 B.一定减小 C.一定增加 D.不能判定
【答案】D
【解析】图中横坐标表示的是摄氏温度.若的延长线与轴相交在,则表示到过程中体积是不变的.但是,由图中无法作出这样的判定.所以,应选D.
【总结升华】一定质量的气体,等容过程中图线是一次线性函数,但并不过原点,其反向延长线与横轴的交点为。
类型二、气体的等压变化,盖一吕萨克定律
例3.如图,竖直放置、开口向上的试管内用水银封闭一段理想气体,若大气压强不变,管内气体( ).
A.温度升高,则体积增大 B.温度升高,则体积减小
C.温度降低,则压强增大 D.温度降低,则压强减小
【思路点拨】属于等压变化.运用盖一吕萨克定律。
【答案】A
【解析】由盖-吕萨克定律知:
增大,则增大,减小,则减小,故A正确。
【总结升华】抓住等压变化时恒量进行分析解题,就一定能作出判断。
举一反三:
【变式】一定质量的气体,如果保持它的压强不变,降低温度,使它的体积为时体积的倍,则此时气体的温度为( ).
A. B.
C. D.
【答案】C
【解析】根据盖一吕萨克定律,在压强不变的条件下,即根据题意,整理后得.
例4.一个开着窗户的房间,温度为时室内空气质量为,当温度升高到时,室内空气的质量为。
【答案】
【解析】应用盖一吕萨克定律,以跑到室外的气体与室内的气体整体为研究对象,设原来体积为,温度升高后体积为,已知,,根据盖—吕萨克定律:
得
.
因温度升高后留在室内的气体体积仍为,占总体积的比例为
.
∴.
【总结升华】解答此类问题关键是将变质量问题从整体角度分析,转化为一定质量的问题,再由等压变化规律求解。
类型三、汞柱移动问题
例5.如图所示,两容器容积相等,用粗细均匀的细玻璃管相连,两容器内装有不同气体,细管中央有一段水银柱,在两边气体作用下保持平衡时,中气体的温度为,中气体温度为,如果将它们的温度都降低,则水银柱将( ).
A.向移动 B.向移动 C.不动 D.不能确定
【思路点拨】假设液柱不动,假设液柱不动,根据查理定律进行分析。
【答案】A
【解析】由,可知.
∴部分气体压强减小得多,左移.
【总结升华】分析解答此类问题的方法是:首先假设液柱不动,假设液柱不动,则两部分气体做等容变化,根据查理定律的分比形式确定,各自压强的变化,从而判定液柱的移动方向。
举一反三:
【变式】如图所示,容器和分别盛有氢气和氧气,用一段竖直细玻璃管连通,管内有一段水银柱将两种气体隔开.当氢气的温度和氧气温度相等时,水银柱保持静止,则当两气体均降低相同的温度时,水银柱将怎样移动?
【答案】向下移动
【解析】假设水银柱不动,由公式分别求出两部分气体的卸值,加以比较进行判断.
对两部分气体:,.
因(对图分析),故,水银柱向容器一方(向下)移动.
【总结升华】判断液柱移动的方向往往采用假设法,假设液柱不动,然后由查理定律的分比形式比较压强的变化,从而判断出液体移动的方向。
例6.如图所示,一端封闭的粗细均匀的玻璃管,开口向上竖直放置,管中有两段水银柱封闭了两段空气柱,开始时,现将玻璃管缓慢地均匀加热,则下述说法中正确的是( ).
A.加热过程中,始终保持
B.加热后,
C.加热后,
D.条件不足,无法确定
【答案】A
【解析】在整个加热过程中,上段气柱的压强始终保持为不变,下段气柱的压强始终为不变,所以整个过程为等压变化,根据盖一吕萨克定律:
得.
得.
∴,即。
【总结升华】解答本题关键是抓住在温度变化时,压强不变,分别对和列方程求解。
举一反三:
【变式】如图所示的玻璃管ABCDE,CD部分水平,其余部分竖直(B端弯曲部分长度可忽略),玻璃管截面半径相比其长度可忽略,CD内有一段水银柱,初始时数据如图,环境温度是300K,大气压是75cmHg。现保持CD水平,将玻璃管A端缓慢竖直向下插入大水银槽中,当水平段水银柱刚好全部进入DE竖直管内时,保持玻璃管静止不动。问:
(1)玻璃管A端插入大水银槽中的深度是多少?(即水银面到管口A的竖直距离)?
(2)当管内气体温度缓慢降低到多少K时,DE中的水银柱刚好回到CD水平管中?
【答案】(1)25cm;(2)T3=262.5K
【解析】(1)以玻璃管内气体为研究对象,设玻璃管横截面积为S,
p1=p0=75cmHg,V1=(140+15+5)S=160S,p2=p0+h1=75+5=80cmHg,
由玻意耳定律可得:p1V1=p2V2,即:75×160S=80×L2S,
L2=150cm,
h=160+10–150+5=25cm; (2)T1=300K,V1=160S,V3=(140+15+10–25)S=140S,
由盖吕萨克定律得:,即,
解得T3=262.5K。
类型四、理解图线的物理意义
例7.一定质量的某种气体自状态经状态变化到状态,这一过程在图上表示如图所示,则( ).
A.在过程中,气体的压强不断变大
B.在过程中,气体的压强不断变小
C.在状态时,气体的压强最大
D.在状态时,气体的压强最大
【思路点拨】用这两个状态到原点连线的斜率大小来判断。
【答案】A、D
【解析】气体在过程中发生等温变化,由可知,体积减小,压强增大,故A正确.在变化过程中,气体的体积不发生变化,即为等容变化,由可知,温度升高,压强增大,故B错误.综上所述,在过程中气体的压强始终增大,所以气体在状态时的压强最大,故C错误,D正确.
【总结升华】在图象中,比较两个状态的压强大小,可以用这两个状态到原点连线的斜率大小来判断,斜率越大、压强越小,斜率越小、压强越大。
举一反三:
【变式】图甲是一定质量的气体由状态经过状态变为状态的图象.已知气体在状态时的压强是.
(1)说出过程中压强变化的情形,并根据图象提供的信息,计算图中的温度值.
(2)请在图乙坐标系中,作出由状态经过状态变为状态的图象,并在图线相应位置上标出字母,如果需要计算才能确定有关坐标值,请写出计算过程.
【答案】(1) (2)见解析
【解析】(1)由图甲可以看出,与的连线的延长线过原点,所以是一个等压变化,即.
根据盖一吕萨克定律可知:
,
∴.
(2)由图甲可知,由是等容变化,根据查理定律得:
.
∴.
则可画出由状态的图象如下图所示。
【总结升华】熟练运用盖—吕萨克定律和查理定律,理解图象和图象的物理意义是解题的关键。
【学习目标】
1.知道什么是等容变化和等压变化;
2.知道查理定律内容及表达式;
3.知道盖一吕萨克定律内容及表达式;
4.知道图象和图象及物理意义;
5.知道热力学温标;
6.熟练利用查理定律及图象和图象分析解决相关问题.
【要点梳理】
要点一、气体的等容变化 查理定律
1.气体的等容变化
气体的等容变化:气体体积保持不变的情况下所发生的状态变化叫等容变化.
2.等容变化规律
(1)实验条件:
气体质量一定;
气体体积不变.
(2)实验过程:
在室温下封闭一定质量的气体在烧瓶中,记下气体的体积和压强.
把烧瓶放入冰水混合物的容器里。记下这时温度为,调整压强计保持气体体积不变,记下压强.如图所示.
把烧瓶放在温度为的温水中,调整压强计保持气体体积不变,记下压强.
(3)实验结论:一定质量的某种气体,在体积不变的条件下,气体的压强随温度升高而增大,随温度降低而减小.
3.摄氏温标下的查理定律
(1)定律:一定质量的某种气体,在体积不变的条件下,气体温度每升高(或降低),增加(或减小)的压强等于气体在时压强的.这条规律叫做查理定律.
(2)公式:或。
其中是温度为时的压强,是时的压强.
(3)等容曲线,如图所示.
要点诠释:图象:一定质量的某种气体,在等容过程中,压强与摄氏温度是一次函数关系,不是简单的正比例关系,等容线是一条延长线通过横轴的倾斜直线,且斜率越大,体积越小.图象纵轴的截距是气体在时的压强.
4.热力学温标下的查理定律
(1)定律:一定质量的气体,在体积不变的条件下,气体的压强跟热力学温度成正比.
(2)公式:,或.
(3)等容曲线,如图所示.
要点诠释:图象:一定质量的某种气体,在等容过程中,气体的压强和热力学温度的图线是过原点的倾斜直线,如图所示,且,即体积越大,斜率越小.
5.查理定律的微观解释
一定质量的气体,说明气体总分子数不变;气体体积不变,则单位体积内的分子数不变;当气体温度升高时,说明分子的平均速率增大,则单位时间内,分子跟器壁单位面积碰撞的次数增多,且每次碰撞器壁产生的平均冲力增大,因此气体压强将增大.
6.查理定律的适用条件
对实际气体,温度不太低(与室温比较),压强不太大(与大气压相比)的情况.
要点二、气体的等压变化,盖一吕萨克定律
1.气体的等压变化
气体在压强不变的情况下所发生的状态变化叫做等压变化.
2.盖一吕萨克定律
(1)一定质量的某种气体,在压强不变的情况下,温度每升高(或降低),增加(或减少)的体积等于它在时体积的,这就是盖一吕萨克定律.其数学表达式为
或.
(2)采用热力学温标时,盖一吕萨克定律可表述为:一定质量的某种气体,在压强不变的情况下,它的体积跟热力学温度成正比.其数学表达式为
或。
(3)适用条件:对于实际气体,温度不太低(与室温比较),压强不太大(与大气压相比)的情况.
3.和图象
(1)图象:一定质量的某种气体,在等压过程中,气体的体积和热力学温度的图线是过原点的倾斜直线,如图甲所示,且,即压强越大,斜率越小.
(2)图象:一定质量的某种气体,在等压过程中,体积与摄氏温度是一次线性函数,不是简单的正比例关系,如图乙所示,图象纵轴的截距是气体在时的体积,等压线是一条延长线通过横轴上的倾斜直线,且斜率越大,压强越小.
要点三、两个重要的推论
(1)一定质量的某种气体,从初状态()开始,发生一个等容变化过程,其压强的变化量与温度的变化量间的关系为
。
这是查理定律的分比形式.
(2)一定质量的某种气体从初状态()开始发生等压变化,其体积的改变量与温度变化量之间的关系是
。
这是盖一吕萨克定律的分比形式.
要点四、利用查理定律和盖一吕萨克定律解题的一般步骤、汞柱移动问题的分析方法
1.利用查理定律和盖一吕萨克定律解题的一般步骤
(1)确定研究对象,即某被封闭气体.
(2)分析状态变化过程,明确初、末状态,确认在状态变化过程中气体的质量和体积保持不变.
(3)分别找出初、末两状态的温度、压强或温度、体积.
(4)根据查理定律和盖一吕萨克定律列方程求解.
(5)分析所求结果是否合理.
2.汞柱移动问题的分析方法
(1)假设法
用液柱或活塞隔开两部分气体,当气体温度变化时,液柱或活塞是否移动?如何移动?此类问题的特点是:气体的状态参量都发生了变化,直接判断液柱或活塞的移动方向比较困难,通常先进行气体状态的假设,然后应用查理定律可以简单地求解.其一般思路为:
①先假设液柱或活塞不发生移动,两部分气体均做等容变化.
②对两部分气体分别应用查理定律的分比形式,求出每部分气体压强的变化量,并加以比较.
③如果液柱两端的横截面积相等,则若均大于零,意味着两部分气体的压强均增大,则液柱向值较小的一方移动;若均小于零,意味着两部分气体的压强均减小,则液柱向压强减小量较大的一方(即||较大的一方)移动;若卸相等,则液柱不移动.
④如果液柱两端的横截面积不相等,则应考虑液柱两端的受力变化(),若均大于零,则液柱向较小的一方移动;若均小于零,则液柱向||值较大的一方移动;若相等,则液柱不移动.
⑤要判断活塞的移动方向,则需要选择好研究对象,进行受力分析,综合应用查理定律和力学规律进行推理和判断.
(2)极限法
所谓极限法就是将问题推向极端.如在讨论压强大小变化时,将变化较大的压强推向无穷大,而将变化较小的压强推向零.这样使复杂的问题变得简单明了.
如图甲所示,两端封闭、粗细均匀、竖直放置的玻璃管内有一段长为的水银柱,将管内气体分为两部分.已知,若使两部分气体同时升高相同的温度,管内水银柱将如何运动?(设原来温度相同)
根据极限法:由于管上段气柱压强较下段气柱压强小,设想,即管上部认为近似为真空,于是立即得到,温度升高,水银柱向上移动.
(3)图象法
利用图象:首先在同一图线上画出两段气柱的等容图线,如图乙所示.由于两气柱在相同温度下压强不同,所以它们等容线的斜率也不同,气柱的压强较大的等容线的斜率也较大.从图中可以看出,当两气柱升高相同温度时,其压强的增量,所以水银柱向压强增量小的一端移动,对图甲的问题用图象法分析,很容易得出水银向上移动的结果.
要点四、理解四种图线的物理意义
(1)图中的等容线:
①图中的等容线是一条延长线通过横坐标的倾斜直线.
②图线中纵轴上的截距凡是气体时的压强.
③等容线的斜率和气体的保持不变的体积大小有关,体积越大,斜率越小,如下图甲四条等容线的关系为:.
(2)图中的等容线
①图中的等容线是一条延长线通过原点的倾斜直线.
②斜率(恒量)与气体体积有关,体积越大,斜率越小.如上图乙所示四条等容线的关系为:.
(3)下图甲所示为图中的等压线,这是一条延长线过的倾斜直线,纵轴上截距表示气体在时的体积.等压线的斜率大小取决于压强的大小,压强越大,斜率越小.图中四条等压线的关系为:.
(4)如上图乙所示为图中的等压线,这是一条延长线通过原点的倾斜直线,直线斜率,斜率越大,恒量越大,压强越小.在图中给出的四条等压线的关系为:.
要点五、知识归纳总结
1.知识网络
2.知识梳理
等容变化过程中查理定律和等压变化过程中盖一吕萨克定律是在实验基础上总结出来的规律,确定一个量不变的情况下另外两个量的比例关系.查理定律中,气体的压强和热力学温度成正比;盖一吕萨克定律中,气体的体积和热力学温度成正比.
【典型例题】
类型一、气体的等容变化 查理定律
例1.密封在容积不变的容器中的气体,当温度降低时( ).
A.压强减小,密度减小 B.压强减小,密度增大
C.压强不变,密度减小 D.压强减小,密度不变
【思路点拨】属于等容变化,运用查理定律。
【答案】 D
【解析】 本题考查的知识点是气体的等容变化.由查理定律得,当体积不变时,热力学温度与压强成正比,因此温度降低时,压强减小.因为质量和体积都不发生变化,因此密度不变.故正确答案为D.
【总结升华】抓住体积不变这一特点,再利用即查理定律作出判断。
举一反三:
【变式1】起飞前高空试验火箭仪器舱内,气压压强,温度.当火箭竖直向上加速飞行()时,仪器舱内水银气压计示数为.已知舱是密封的,可以判定此时舱内的温度是________.
【答案】
【解析】加速前后,仪器舱内气体做的是等容变化,可以用查理定律求加速时舱内温度.
取舱内气体为研究对象,由查理定律得
. ①
取气压计内高出液面的水银柱为研究对象,由牛顿第二定律得
. ②
又
. ③
由①②③得,.
【总结升华】挖掘出舱内气体做等容变化是解题的关键,其次要灵活运用液体压强公式。
【变式2】电灯泡内充有氮、氩混合气体,如果要使灯泡内的混合气体在时的压强不超过一个大气压,则在的室温下充气,电灯泡内气体压强至多能充到多少?
【答案】见解析
【解析】忽略灯泡容积的变化,气体为等容变化,找出气体的初、末状态,运用查理定律的两种表述皆可求解.
设时气体的压强为,时气体的压强为,时气体的压强为.由查理定律
可得
,.
所以
.
故
.
【总结升华】 ①一定质量的某种气体在体积不变的情况下,压强跟热力学温度成正比,即(常数)或。
②在查理定律的第一种表述中,气体的温度是热力学温度,而在第二种表述中则是摄氏温度,而且式中是时气体的压强,并非气体初状态的压强。
例2.如图所示是一定质量的理想气体的三种升温过程,那么,以下四种解释中,哪些是正确的?( ).
A.的过程气体体积增加 B.的过程气体体积不变
C.的过程气体体积增加 D.的过程气体体积减小
【答案】A、B
【解析】在图上的等容线的延长线是过原点的直线,且体积越大,直线的斜率越小.由此可见,状态对应体积最小,状态对应体积最大.所以选项A、B是正确的.
【总结升华】一定质量的气体,等容过程中图线是过原点的倾斜直线,其斜率越大,体积越小。
举一反三:
【变式】一定质量的理想气体的图象,如图所示,在气体由状态变化到状态的过程中,体积怎样变化?( ).
A.一定不变 B.一定减小 C.一定增加 D.不能判定
【答案】D
【解析】图中横坐标表示的是摄氏温度.若的延长线与轴相交在,则表示到过程中体积是不变的.但是,由图中无法作出这样的判定.所以,应选D.
【总结升华】一定质量的气体,等容过程中图线是一次线性函数,但并不过原点,其反向延长线与横轴的交点为。
类型二、气体的等压变化,盖一吕萨克定律
例3.如图,竖直放置、开口向上的试管内用水银封闭一段理想气体,若大气压强不变,管内气体( ).
A.温度升高,则体积增大 B.温度升高,则体积减小
C.温度降低,则压强增大 D.温度降低,则压强减小
【思路点拨】属于等压变化.运用盖一吕萨克定律。
【答案】A
【解析】由盖-吕萨克定律知:
增大,则增大,减小,则减小,故A正确。
【总结升华】抓住等压变化时恒量进行分析解题,就一定能作出判断。
举一反三:
【变式】一定质量的气体,如果保持它的压强不变,降低温度,使它的体积为时体积的倍,则此时气体的温度为( ).
A. B.
C. D.
【答案】C
【解析】根据盖一吕萨克定律,在压强不变的条件下,即根据题意,整理后得.
例4.一个开着窗户的房间,温度为时室内空气质量为,当温度升高到时,室内空气的质量为。
【答案】
【解析】应用盖一吕萨克定律,以跑到室外的气体与室内的气体整体为研究对象,设原来体积为,温度升高后体积为,已知,,根据盖—吕萨克定律:
得
.
因温度升高后留在室内的气体体积仍为,占总体积的比例为
.
∴.
【总结升华】解答此类问题关键是将变质量问题从整体角度分析,转化为一定质量的问题,再由等压变化规律求解。
类型三、汞柱移动问题
例5.如图所示,两容器容积相等,用粗细均匀的细玻璃管相连,两容器内装有不同气体,细管中央有一段水银柱,在两边气体作用下保持平衡时,中气体的温度为,中气体温度为,如果将它们的温度都降低,则水银柱将( ).
A.向移动 B.向移动 C.不动 D.不能确定
【思路点拨】假设液柱不动,假设液柱不动,根据查理定律进行分析。
【答案】A
【解析】由,可知.
∴部分气体压强减小得多,左移.
【总结升华】分析解答此类问题的方法是:首先假设液柱不动,假设液柱不动,则两部分气体做等容变化,根据查理定律的分比形式确定,各自压强的变化,从而判定液柱的移动方向。
举一反三:
【变式】如图所示,容器和分别盛有氢气和氧气,用一段竖直细玻璃管连通,管内有一段水银柱将两种气体隔开.当氢气的温度和氧气温度相等时,水银柱保持静止,则当两气体均降低相同的温度时,水银柱将怎样移动?
【答案】向下移动
【解析】假设水银柱不动,由公式分别求出两部分气体的卸值,加以比较进行判断.
对两部分气体:,.
因(对图分析),故,水银柱向容器一方(向下)移动.
【总结升华】判断液柱移动的方向往往采用假设法,假设液柱不动,然后由查理定律的分比形式比较压强的变化,从而判断出液体移动的方向。
例6.如图所示,一端封闭的粗细均匀的玻璃管,开口向上竖直放置,管中有两段水银柱封闭了两段空气柱,开始时,现将玻璃管缓慢地均匀加热,则下述说法中正确的是( ).
A.加热过程中,始终保持
B.加热后,
C.加热后,
D.条件不足,无法确定
【答案】A
【解析】在整个加热过程中,上段气柱的压强始终保持为不变,下段气柱的压强始终为不变,所以整个过程为等压变化,根据盖一吕萨克定律:
得.
得.
∴,即。
【总结升华】解答本题关键是抓住在温度变化时,压强不变,分别对和列方程求解。
举一反三:
【变式】如图所示的玻璃管ABCDE,CD部分水平,其余部分竖直(B端弯曲部分长度可忽略),玻璃管截面半径相比其长度可忽略,CD内有一段水银柱,初始时数据如图,环境温度是300K,大气压是75cmHg。现保持CD水平,将玻璃管A端缓慢竖直向下插入大水银槽中,当水平段水银柱刚好全部进入DE竖直管内时,保持玻璃管静止不动。问:
(1)玻璃管A端插入大水银槽中的深度是多少?(即水银面到管口A的竖直距离)?
(2)当管内气体温度缓慢降低到多少K时,DE中的水银柱刚好回到CD水平管中?
【答案】(1)25cm;(2)T3=262.5K
【解析】(1)以玻璃管内气体为研究对象,设玻璃管横截面积为S,
p1=p0=75cmHg,V1=(140+15+5)S=160S,p2=p0+h1=75+5=80cmHg,
由玻意耳定律可得:p1V1=p2V2,即:75×160S=80×L2S,
L2=150cm,
h=160+10–150+5=25cm; (2)T1=300K,V1=160S,V3=(140+15+10–25)S=140S,
由盖吕萨克定律得:,即,
解得T3=262.5K。
类型四、理解图线的物理意义
例7.一定质量的某种气体自状态经状态变化到状态,这一过程在图上表示如图所示,则( ).
A.在过程中,气体的压强不断变大
B.在过程中,气体的压强不断变小
C.在状态时,气体的压强最大
D.在状态时,气体的压强最大
【思路点拨】用这两个状态到原点连线的斜率大小来判断。
【答案】A、D
【解析】气体在过程中发生等温变化,由可知,体积减小,压强增大,故A正确.在变化过程中,气体的体积不发生变化,即为等容变化,由可知,温度升高,压强增大,故B错误.综上所述,在过程中气体的压强始终增大,所以气体在状态时的压强最大,故C错误,D正确.
【总结升华】在图象中,比较两个状态的压强大小,可以用这两个状态到原点连线的斜率大小来判断,斜率越大、压强越小,斜率越小、压强越大。
举一反三:
【变式】图甲是一定质量的气体由状态经过状态变为状态的图象.已知气体在状态时的压强是.
(1)说出过程中压强变化的情形,并根据图象提供的信息,计算图中的温度值.
(2)请在图乙坐标系中,作出由状态经过状态变为状态的图象,并在图线相应位置上标出字母,如果需要计算才能确定有关坐标值,请写出计算过程.
【答案】(1) (2)见解析
【解析】(1)由图甲可以看出,与的连线的延长线过原点,所以是一个等压变化,即.
根据盖一吕萨克定律可知:
,
∴.
(2)由图甲可知,由是等容变化,根据查理定律得:
.
∴.
则可画出由状态的图象如下图所示。
【总结升华】熟练运用盖—吕萨克定律和查理定律,理解图象和图象的物理意义是解题的关键。
等容变化和等压变化
【学习目标】
1.知道什么是等容变化和等压变化;
2.知道查理定律内容及表达式;
3.知道盖一吕萨克定律内容及表达式;
4.知道图象和图象及物理意义;
5.知道热力学温标;
6.熟练利用查理定律及图象和图象分析解决相关问题.
【要点梳理】
要点一、气体的等容变化 查理定律
1.气体的等容变化
气体的等容变化:气体体积保持不变的情况下所发生的状态变化叫等容变化.
2.等容变化规律
(1)实验条件:
气体质量一定;
气体体积不变.
(2)实验过程:
在室温下封闭一定质量的气体在烧瓶中,记下气体的体积和压强.
把烧瓶放入冰水混合物的容器里。记下这时温度为,调整压强计保持气体体积不变,记下压强.如图所示.
把烧瓶放在温度为的温水中,调整压强计保持气体体积不变,记下压强.
(3)实验结论:一定质量的某种气体,在体积不变的条件下,气体的压强随温度升高而增大,随温度降低而减小.
3.摄氏温标下的查理定律
(1)定律:一定质量的某种气体,在体积不变的条件下,气体温度每升高(或降低),增加(或减小)的压强等于气体在时压强的.这条规律叫做查理定律.
(2)公式:或。
其中是温度为时的压强,是时的压强.
(3)等容曲线,如图所示.
要点诠释:图象:一定质量的某种气体,在等容过程中,压强与摄氏温度是一次函数关系,不是简单的正比例关系,等容线是一条延长线通过横轴的倾斜直线,且斜率越大,体积越小.图象纵轴的截距是气体在时的压强.
4.热力学温标下的查理定律
(1)定律:一定质量的气体,在体积不变的条件下,气体的压强跟热力学温度成正比.
(2)公式:,或.
(3)等容曲线,如图所示.
要点诠释:图象:一定质量的某种气体,在等容过程中,气体的压强和热力学温度的图线是过原点的倾斜直线,如图所示,且,即体积越大,斜率越小.
5.查理定律的微观解释
一定质量的气体,说明气体总分子数不变;气体体积不变,则单位体积内的分子数不变;当气体温度升高时,说明分子的平均速率增大,则单位时间内,分子跟器壁单位面积碰撞的次数增多,且每次碰撞器壁产生的平均冲力增大,因此气体压强将增大.
6.查理定律的适用条件
对实际气体,温度不太低(与室温比较),压强不太大(与大气压相比)的情况.
要点二、气体的等压变化,盖一吕萨克定律
1.气体的等压变化
气体在压强不变的情况下所发生的状态变化叫做等压变化.
2.盖一吕萨克定律
(1)一定质量的某种气体,在压强不变的情况下,温度每升高(或降低),增加(或减少)的体积等于它在时体积的,这就是盖一吕萨克定律.其数学表达式为
或.
(2)采用热力学温标时,盖一吕萨克定律可表述为:一定质量的某种气体,在压强不变的情况下,它的体积跟热力学温度成正比.其数学表达式为
或。
(3)适用条件:对于实际气体,温度不太低(与室温比较),压强不太大(与大气压相比)的情况.
3.和图象
(1)图象:一定质量的某种气体,在等压过程中,气体的体积和热力学温度的图线是过原点的倾斜直线,如图甲所示,且,即压强越大,斜率越小.
(2)图象:一定质量的某种气体,在等压过程中,体积与摄氏温度是一次线性函数,不是简单的正比例关系,如图乙所示,图象纵轴的截距是气体在时的体积,等压线是一条延长线通过横轴上的倾斜直线,且斜率越大,压强越小.
要点三、两个重要的推论
(1)一定质量的某种气体,从初状态()开始,发生一个等容变化过程,其压强的变化量与温度的变化量间的关系为
。
这是查理定律的分比形式.
(2)一定质量的某种气体从初状态()开始发生等压变化,其体积的改变量与温度变化量之间的关系是
。
这是盖一吕萨克定律的分比形式.
要点四、利用查理定律和盖一吕萨克定律解题的一般步骤、汞柱移动问题的分析方法
1.利用查理定律和盖一吕萨克定律解题的一般步骤
(1)确定研究对象,即某被封闭气体.
(2)分析状态变化过程,明确初、末状态,确认在状态变化过程中气体的质量和体积保持不变.
(3)分别找出初、末两状态的温度、压强或温度、体积.
(4)根据查理定律和盖一吕萨克定律列方程求解.
(5)分析所求结果是否合理.
2.汞柱移动问题的分析方法
(1)假设法
用液柱或活塞隔开两部分气体,当气体温度变化时,液柱或活塞是否移动?如何移动?此类问题的特点是:气体的状态参量都发生了变化,直接判断液柱或活塞的移动方向比较困难,通常先进行气体状态的假设,然后应用查理定律可以简单地求解.其一般思路为:
①先假设液柱或活塞不发生移动,两部分气体均做等容变化.
②对两部分气体分别应用查理定律的分比形式,求出每部分气体压强的变化量,并加以比较.
③如果液柱两端的横截面积相等,则若均大于零,意味着两部分气体的压强均增大,则液柱向值较小的一方移动;若均小于零,意味着两部分气体的压强均减小,则液柱向压强减小量较大的一方(即||较大的一方)移动;若卸相等,则液柱不移动.
④如果液柱两端的横截面积不相等,则应考虑液柱两端的受力变化(),若均大于零,则液柱向较小的一方移动;若均小于零,则液柱向||值较大的一方移动;若相等,则液柱不移动.
⑤要判断活塞的移动方向,则需要选择好研究对象,进行受力分析,综合应用查理定律和力学规律进行推理和判断.
(2)极限法
所谓极限法就是将问题推向极端.如在讨论压强大小变化时,将变化较大的压强推向无穷大,而将变化较小的压强推向零.这样使复杂的问题变得简单明了.
如图甲所示,两端封闭、粗细均匀、竖直放置的玻璃管内有一段长为的水银柱,将管内气体分为两部分.已知,若使两部分气体同时升高相同的温度,管内水银柱将如何运动?(设原来温度相同)
根据极限法:由于管上段气柱压强较下段气柱压强小,设想,即管上部认为近似为真空,于是立即得到,温度升高,水银柱向上移动.
(3)图象法
利用图象:首先在同一图线上画出两段气柱的等容图线,如图乙所示.由于两气柱在相同温度下压强不同,所以它们等容线的斜率也不同,气柱的压强较大的等容线的斜率也较大.从图中可以看出,当两气柱升高相同温度时,其压强的增量,所以水银柱向压强增量小的一端移动,对图甲的问题用图象法分析,很容易得出水银向上移动的结果.
要点四、理解四种图线的物理意义
(1)图中的等容线:
①图中的等容线是一条延长线通过横坐标的倾斜直线.
②图线中纵轴上的截距凡是气体时的压强.
③等容线的斜率和气体的保持不变的体积大小有关,体积越大,斜率越小,如下图甲四条等容线的关系为:.
(2)图中的等容线
①图中的等容线是一条延长线通过原点的倾斜直线.
②斜率(恒量)与气体体积有关,体积越大,斜率越小.如上图乙所示四条等容线的关系为:.
(3)下图甲所示为图中的等压线,这是一条延长线过的倾斜直线,纵轴上截距表示气体在时的体积.等压线的斜率大小取决于压强的大小,压强越大,斜率越小.图中四条等压线的关系为:.
(4)如上图乙所示为图中的等压线,这是一条延长线通过原点的倾斜直线,直线斜率,斜率越大,恒量越大,压强越小.在图中给出的四条等压线的关系为:.
要点五、知识归纳总结
1.知识网络
2.知识梳理
等容变化过程中查理定律和等压变化过程中盖一吕萨克定律是在实验基础上总结出来的规律,确定一个量不变的情况下另外两个量的比例关系.查理定律中,气体的压强和热力学温度成正比;盖一吕萨克定律中,气体的体积和热力学温度成正比.
【典型例题】
类型一、气体的等容变化 查理定律
例1.密封在容积不变的容器中的气体,当温度降低时( ).
A.压强减小,密度减小 B.压强减小,密度增大
C.压强不变,密度减小 D.压强减小,密度不变
【思路点拨】属于等容变化,运用查理定律。
【答案】 D
【解析】 本题考查的知识点是气体的等容变化.由查理定律得,当体积不变时,热力学温度与压强成正比,因此温度降低时,压强减小.因为质量和体积都不发生变化,因此密度不变.故正确答案为D.
【总结升华】抓住体积不变这一特点,再利用即查理定律作出判断。
举一反三:
【变式1】起飞前高空试验火箭仪器舱内,气压压强,温度.当火箭竖直向上加速飞行()时,仪器舱内水银气压计示数为.已知舱是密封的,可以判定此时舱内的温度是________.
【答案】
【解析】加速前后,仪器舱内气体做的是等容变化,可以用查理定律求加速时舱内温度.
取舱内气体为研究对象,由查理定律得
. ①
取气压计内高出液面的水银柱为研究对象,由牛顿第二定律得
. ②
又
. ③
由①②③得,.
【总结升华】挖掘出舱内气体做等容变化是解题的关键,其次要灵活运用液体压强公式。
【变式2】电灯泡内充有氮、氩混合气体,如果要使灯泡内的混合气体在时的压强不超过一个大气压,则在的室温下充气,电灯泡内气体压强至多能充到多少?
【答案】见解析
【解析】忽略灯泡容积的变化,气体为等容变化,找出气体的初、末状态,运用查理定律的两种表述皆可求解.
设时气体的压强为,时气体的压强为,时气体的压强为.由查理定律
可得
,.
所以
.
故
.
【总结升华】 ①一定质量的某种气体在体积不变的情况下,压强跟热力学温度成正比,即(常数)或。
②在查理定律的第一种表述中,气体的温度是热力学温度,而在第二种表述中则是摄氏温度,而且式中是时气体的压强,并非气体初状态的压强。
例2.如图所示是一定质量的理想气体的三种升温过程,那么,以下四种解释中,哪些是正确的?( ).
A.的过程气体体积增加 B.的过程气体体积不变
C.的过程气体体积增加 D.的过程气体体积减小
【答案】A、B
【解析】在图上的等容线的延长线是过原点的直线,且体积越大,直线的斜率越小.由此可见,状态对应体积最小,状态对应体积最大.所以选项A、B是正确的.
【总结升华】一定质量的气体,等容过程中图线是过原点的倾斜直线,其斜率越大,体积越小。
举一反三:
【变式】一定质量的理想气体的图象,如图所示,在气体由状态变化到状态的过程中,体积怎样变化?( ).
A.一定不变 B.一定减小 C.一定增加 D.不能判定
【答案】D
【解析】图中横坐标表示的是摄氏温度.若的延长线与轴相交在,则表示到过程中体积是不变的.但是,由图中无法作出这样的判定.所以,应选D.
【总结升华】一定质量的气体,等容过程中图线是一次线性函数,但并不过原点,其反向延长线与横轴的交点为。
类型二、气体的等压变化,盖一吕萨克定律
例3.如图,竖直放置、开口向上的试管内用水银封闭一段理想气体,若大气压强不变,管内气体( ).
A.温度升高,则体积增大 B.温度升高,则体积减小
C.温度降低,则压强增大 D.温度降低,则压强减小
【思路点拨】属于等压变化.运用盖一吕萨克定律。
【答案】A
【解析】由盖-吕萨克定律知:
增大,则增大,减小,则减小,故A正确。
【总结升华】抓住等压变化时恒量进行分析解题,就一定能作出判断。
举一反三:
【变式】一定质量的气体,如果保持它的压强不变,降低温度,使它的体积为时体积的倍,则此时气体的温度为( ).
A. B.
C. D.
【答案】C
【解析】根据盖一吕萨克定律,在压强不变的条件下,即根据题意,整理后得.
例4.一个开着窗户的房间,温度为时室内空气质量为,当温度升高到时,室内空气的质量为。
【答案】
【解析】应用盖一吕萨克定律,以跑到室外的气体与室内的气体整体为研究对象,设原来体积为,温度升高后体积为,已知,,根据盖—吕萨克定律:
得
.
因温度升高后留在室内的气体体积仍为,占总体积的比例为
.
∴.
【总结升华】解答此类问题关键是将变质量问题从整体角度分析,转化为一定质量的问题,再由等压变化规律求解。
类型三、汞柱移动问题
例5.如图所示,两容器容积相等,用粗细均匀的细玻璃管相连,两容器内装有不同气体,细管中央有一段水银柱,在两边气体作用下保持平衡时,中气体的温度为,中气体温度为,如果将它们的温度都降低,则水银柱将( ).
A.向移动 B.向移动 C.不动 D.不能确定
【思路点拨】假设液柱不动,假设液柱不动,根据查理定律进行分析。
【答案】A
【解析】由,可知.
∴部分气体压强减小得多,左移.
【总结升华】分析解答此类问题的方法是:首先假设液柱不动,假设液柱不动,则两部分气体做等容变化,根据查理定律的分比形式确定,各自压强的变化,从而判定液柱的移动方向。
举一反三:
【变式】如图所示,容器和分别盛有氢气和氧气,用一段竖直细玻璃管连通,管内有一段水银柱将两种气体隔开.当氢气的温度和氧气温度相等时,水银柱保持静止,则当两气体均降低相同的温度时,水银柱将怎样移动?
【答案】向下移动
【解析】假设水银柱不动,由公式分别求出两部分气体的卸值,加以比较进行判断.
对两部分气体:,.
因(对图分析),故,水银柱向容器一方(向下)移动.
【总结升华】判断液柱移动的方向往往采用假设法,假设液柱不动,然后由查理定律的分比形式比较压强的变化,从而判断出液体移动的方向。
例6.如图所示,一端封闭的粗细均匀的玻璃管,开口向上竖直放置,管中有两段水银柱封闭了两段空气柱,开始时,现将玻璃管缓慢地均匀加热,则下述说法中正确的是( ).
A.加热过程中,始终保持
B.加热后,
C.加热后,
D.条件不足,无法确定
【答案】A
【解析】在整个加热过程中,上段气柱的压强始终保持为不变,下段气柱的压强始终为不变,所以整个过程为等压变化,根据盖一吕萨克定律:
得.
得.
∴,即。
【总结升华】解答本题关键是抓住在温度变化时,压强不变,分别对和列方程求解。
举一反三:
【变式】如图所示的玻璃管ABCDE,CD部分水平,其余部分竖直(B端弯曲部分长度可忽略),玻璃管截面半径相比其长度可忽略,CD内有一段水银柱,初始时数据如图,环境温度是300K,大气压是75cmHg。现保持CD水平,将玻璃管A端缓慢竖直向下插入大水银槽中,当水平段水银柱刚好全部进入DE竖直管内时,保持玻璃管静止不动。问:
(1)玻璃管A端插入大水银槽中的深度是多少?(即水银面到管口A的竖直距离)?
(2)当管内气体温度缓慢降低到多少K时,DE中的水银柱刚好回到CD水平管中?
【答案】(1)25cm;(2)T3=262.5K
【解析】(1)以玻璃管内气体为研究对象,设玻璃管横截面积为S,
p1=p0=75cmHg,V1=(140+15+5)S=160S,p2=p0+h1=75+5=80cmHg,
由玻意耳定律可得:p1V1=p2V2,即:75×160S=80×L2S,
L2=150cm,
h=160+10–150+5=25cm; (2)T1=300K,V1=160S,V3=(140+15+10–25)S=140S,
由盖吕萨克定律得:,即,
解得T3=262.5K。
类型四、理解图线的物理意义
例7.一定质量的某种气体自状态经状态变化到状态,这一过程在图上表示如图所示,则( ).
A.在过程中,气体的压强不断变大
B.在过程中,气体的压强不断变小
C.在状态时,气体的压强最大
D.在状态时,气体的压强最大
【思路点拨】用这两个状态到原点连线的斜率大小来判断。
【答案】A、D
【解析】气体在过程中发生等温变化,由可知,体积减小,压强增大,故A正确.在变化过程中,气体的体积不发生变化,即为等容变化,由可知,温度升高,压强增大,故B错误.综上所述,在过程中气体的压强始终增大,所以气体在状态时的压强最大,故C错误,D正确.
【总结升华】在图象中,比较两个状态的压强大小,可以用这两个状态到原点连线的斜率大小来判断,斜率越大、压强越小,斜率越小、压强越大。
举一反三:
【变式】图甲是一定质量的气体由状态经过状态变为状态的图象.已知气体在状态时的压强是.
(1)说出过程中压强变化的情形,并根据图象提供的信息,计算图中的温度值.
(2)请在图乙坐标系中,作出由状态经过状态变为状态的图象,并在图线相应位置上标出字母,如果需要计算才能确定有关坐标值,请写出计算过程.
【答案】(1) (2)见解析
【解析】(1)由图甲可以看出,与的连线的延长线过原点,所以是一个等压变化,即.
根据盖一吕萨克定律可知:
,
∴.
(2)由图甲可知,由是等容变化,根据查理定律得:
.
∴.
则可画出由状态的图象如下图所示。
【总结升华】熟练运用盖—吕萨克定律和查理定律,理解图象和图象的物理意义是解题的关键。
同课章节目录
- 第一章 分子动理论与统计思想
- 1 物体是由大量分子组成的
- 2 分子的热运动
- 3 分子间的相互作用力
- 4 统计规律 分子运动速率分布
- 5 温度 内能 气体的压强
- 6 实验探究:用油膜法估测油酸分子的大小
- 第二章 固体和液体
- 1 晶体和非晶体
- 2 半导体
- 3 液体的表面张力
- 4 液晶
- 第三章 气体
- 1 气体实验定律
- 2 气体实验定律的微观解释及图像表示
- 3 理想气体
- 4 饱各汽与未饱和汽
- 5 空气的温度
- 第四章 能量守恒与热力学定律
- 1 能量守恒定律的发现
- 2 热力学第一定律
- 3 宏观热过程的方向性
- 4 热力学第二定律
- 5 熵概念初步
- 第五章 能源与可持续发展
- 1 能源与人类生存的关系
- 2 能源利用与环境问题
- 3 可持续发展战略
