2018高中物理第二章力力的合成与分解练习(提高篇)教科版必修1
文档属性
| 名称 | 2018高中物理第二章力力的合成与分解练习(提高篇)教科版必修1 |
|
|
| 格式 | zip | ||
| 文件大小 | 254.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-09-05 00:00:00 | ||
图片预览

文档简介
力的合成与分解(提高篇)
一、选择题:
1. 关于F1、F2及它们的合力F,下列说法中正确的是( )
A.合力F一定与F1、F2共同作用产生的效果相同
B.两力F1、F2一定是同种性质的力
C.两力F1、F2一定是同一个物体受到的力
D.两力F1、F2与F是物体同时受到的三个力
2. 两个共点力的大小分别为F1和F2,作用于物体的同一点.两力同向时,合力为A,两力反向时,合力为B,当两力互相垂直时合力为( )
A. B. C. D.
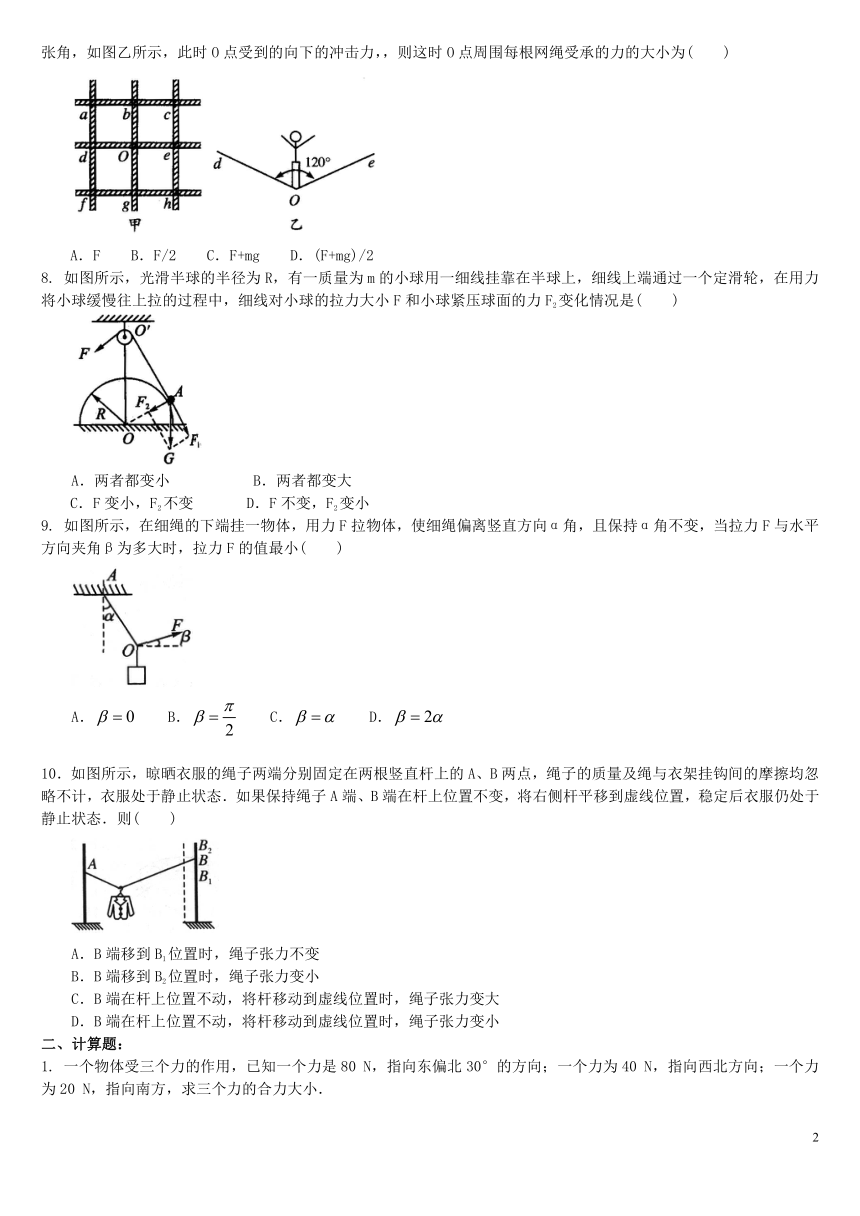
3. 水平横梁一端插在墙壁内,另一端装小滑轮B.一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=10kg的重物,∠CBA=30°,如图所示,则滑轮受到绳子的作用力为(g=10N/kg)( )
A.50 N B.N C.100 N D.N
4. 物体同时受到同一平面内的三个共点力的作用,下列几组力的合力不可能为零的是( )
A.5 N,7 N,8 N B.5 N,2 N,3 N
C.1 N,5 N,10 N D.10 N,10 N,10 N
5. 2008年北京奥运会,我国运动员陈一冰勇夺吊环冠军,其中有一个高难度的动作就是先双手撑住吊环,然后身体下移,双臂缓慢张开到如图所示位置,则在两手之间的距离增大过程中,吊环的两根绳的拉力T(两个拉力大小相等)及它们的合力F的大小变化情况为( )
A.T增大,F不变 B.T增大,F增大 C.T增大,F减小 D.T减小,F不变
6. 如图所示,物体M在斜向右下方的推力F作用下,在水平地面上恰好做匀速运动,则推力F和物体M受到的摩擦力的合力方向是( )
A.竖直向下 B.竖直向上
C.斜向下偏左 D.斜向下偏右
7. 如图所示,甲为杂技表演的安全网示意图,网绳的结构为正方格形,O,a,b,c,d,…为网绳的结点,安全网水平张紧后,若质量为m的演员从高处落下,并恰好落在O点上,该处下凹最低点时,网绳dOe,bOg均为120°向上的张角,如图乙所示,此时O点受到的向下的冲击力,,则这时O点周围每根网绳受承的力的大小为( )
A.F B.F/2 C.F+mg D.(F+mg)/2
8. 如图所示,光滑半球的半径为R,有一质量为m的小球用一细线挂靠在半球上,细线上端通过一个定滑轮,在用力将小球缓慢往上拉的过程中,细线对小球的拉力大小F和小球紧压球面的力F2变化情况是( )
A.两者都变小 B.两者都变大
C.F变小,F2不变 D.F不变,F2变小
9. 如图所示,在细绳的下端挂一物体,用力F拉物体,使细绳偏离竖直方向α角,且保持α角不变,当拉力F与水平方向夹角β为多大时,拉力F的值最小( )
A. B. C. D.
10.如图所示,晾晒衣服的绳子两端分别固定在两根竖直杆上的A、B两点,绳子的质量及绳与衣架挂钩间的摩擦均忽略不计,衣服处于静止状态.如果保持绳子A端、B端在杆上位置不变,将右侧杆平移到虚线位置,稳定后衣服仍处于静止状态.则( )
A.B端移到B1位置时,绳子张力不变
B.B端移到B2位置时,绳子张力变小
C.B端在杆上位置不动,将杆移动到虚线位置时,绳子张力变大
D.B端在杆上位置不动,将杆移动到虚线位置时,绳子张力变小
二、计算题:
1. 一个物体受三个力的作用,已知一个力是80 N,指向东偏北30°的方向;一个力为40 N,指向西北方向;一个力为20 N,指向南方,求三个力的合力大小.
2. 两人在两岸用绳拉小船在河流中行驶.如图所示,已知甲的拉力是200 N,拉力方向与航向夹角为60°,乙的拉力大小为N,且两绳在同一水平面内,若要使小船能在河流正中间沿直线行驶,乙用力的方向如何?小船受到两拉力的合力为多大?
【答案与解析】
选择题:
1.AC
解析:只有同一个物体受到的力才能合成,分别作用在不同物体上的力不能合成.合力是对原来几个分力的等效替代,两力可以是不同性质的力,但合力与分力不能同时存在.所以,正确选项为A、C.
2. B
解析:由题意知 F1+F2=A,F1-F2=B,
故,.
当两力互相垂直时,
合力
3. C
解析:以滑轮为研究对象,悬挂重物的绳的拉力是F=mg=100N,故小滑轮受到绳的作用力沿BC、BD方向,大小都是100N.从下图中可看出∠CBD=120°,∠CBE=∠DBE得∠CBE=∠DBE=60°,即△CBE是等边三角形,故100N.
4.C
解析:三力合成,若前面力的合力可与第三力大小相等,方向相反,就可以使这三力的合力为零,只要使第三力在其他两力的合力范围之内,就可能使合力为零,即第三力F3满足:|F1-F2|≤F3≤F1+F2.选项A中,前两力合力范围是:2N≤≤12N,第三力在其范围之内;选项B中,前两力合力范围是:3N≤≤7N,第三力在其合力范围之内;选项C中,前两力合力范围是:4N≤≤6N,第三力不在其合力范围之内;选项D中,前两力合力范围是:0≤≤20N,第三力在其合力范围之内,故只有C中第三力不在前两力合力范围之内,即C项中的三力合力不可能为零.
5. A
解析:两绳拉力的合力大小F与重力大小相等,故合力F不变.但由于两手间距增大,使两绳拉力的夹角增大,要使合力不变,则两绳拉力应增大,即T增大.故选项A正确.
6. A
解析:物体M受四个力作用,支持力和重力都在竖直方向上,故推力F与摩擦力的合力一定在竖直方向上,由于推力F的方向斜向下,由此可断定力F与摩擦力的合力一定竖直向下.
7. B
解析:D结点处有四根网绳,是∠dDe=∠bOg=120°,因此每根绳中承受力为F/2.注意冲击力F中已包含mg的作用效果.
8. C
解析:在小球往上移动的过程中,小球所受的重力不变,拉力F与重力的分力F1大小相等、方向相反,并且随着小球上移,F1与F2的方向均发生变化,此时力的平行四边形的形状变化规律不直观,力随角度变化的关系也难建立.而此处所求的力的变化关系是由于O′A段细线缩短引起的,因此可建立与O′A线段长之间的变化关系.如图所示,设O′A段长为L,小球半径为r,O′点到半球顶的距离为d.利用三角形相似得 .
当小球往上移动时,L减小,d、r和R都不变,因此F1减小(即F减小)、F2不变,故选项C正确.
9. C
解析:由题意知,O点所受的合力在拉力F方向变化的过程中始终为零.如下图所示,在拉力F方向变化过程中,OA绳的拉力与拉力F的合力F′总等于物体重力的大小,所以,本题转化为已知合力求分力的问题,由下图可知:拉力F方向垂直于绳的拉力时,F有最小值,此时.
10.AD
解析:挂钩相当于滑轮,轻绳两端对衣架挂钩的拉力大小相等,由平行四边形定则可知:重力的反向延长线将绳子的夹角θ平分,如图所示,设绳子长度为L,两杆之间的距离为d,由几何关系可得:.
B端上下移动时,d和L不变,夹角θ不变,绳子张力不变;杆移到虚线位置时,d减小而L不变,夹角θ变小,绳子张力变小.故选项A、D正确.
二、计算题:
1. 63.34N
解析:物体受力示意图如图所示.取向东方向为x轴正方向,向北方向为y轴正方向,建立直角坐标系,如图所示.将F1、F2进行正交分解.
由图可知
,.
,.
,.
x方向的合力为
.
y方向的合力为
.
最后三个力的合力为.
2. 400N
解析:此题可用正交分解的方法处理,要小船能在河流正中间沿直线行驶,则垂直河流方向合力应为零,则,故,而合力
一、选择题:
1. 关于F1、F2及它们的合力F,下列说法中正确的是( )
A.合力F一定与F1、F2共同作用产生的效果相同
B.两力F1、F2一定是同种性质的力
C.两力F1、F2一定是同一个物体受到的力
D.两力F1、F2与F是物体同时受到的三个力
2. 两个共点力的大小分别为F1和F2,作用于物体的同一点.两力同向时,合力为A,两力反向时,合力为B,当两力互相垂直时合力为( )
A. B. C. D.
3. 水平横梁一端插在墙壁内,另一端装小滑轮B.一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=10kg的重物,∠CBA=30°,如图所示,则滑轮受到绳子的作用力为(g=10N/kg)( )
A.50 N B.N C.100 N D.N
4. 物体同时受到同一平面内的三个共点力的作用,下列几组力的合力不可能为零的是( )
A.5 N,7 N,8 N B.5 N,2 N,3 N
C.1 N,5 N,10 N D.10 N,10 N,10 N
5. 2008年北京奥运会,我国运动员陈一冰勇夺吊环冠军,其中有一个高难度的动作就是先双手撑住吊环,然后身体下移,双臂缓慢张开到如图所示位置,则在两手之间的距离增大过程中,吊环的两根绳的拉力T(两个拉力大小相等)及它们的合力F的大小变化情况为( )
A.T增大,F不变 B.T增大,F增大 C.T增大,F减小 D.T减小,F不变
6. 如图所示,物体M在斜向右下方的推力F作用下,在水平地面上恰好做匀速运动,则推力F和物体M受到的摩擦力的合力方向是( )
A.竖直向下 B.竖直向上
C.斜向下偏左 D.斜向下偏右
7. 如图所示,甲为杂技表演的安全网示意图,网绳的结构为正方格形,O,a,b,c,d,…为网绳的结点,安全网水平张紧后,若质量为m的演员从高处落下,并恰好落在O点上,该处下凹最低点时,网绳dOe,bOg均为120°向上的张角,如图乙所示,此时O点受到的向下的冲击力,,则这时O点周围每根网绳受承的力的大小为( )
A.F B.F/2 C.F+mg D.(F+mg)/2
8. 如图所示,光滑半球的半径为R,有一质量为m的小球用一细线挂靠在半球上,细线上端通过一个定滑轮,在用力将小球缓慢往上拉的过程中,细线对小球的拉力大小F和小球紧压球面的力F2变化情况是( )
A.两者都变小 B.两者都变大
C.F变小,F2不变 D.F不变,F2变小
9. 如图所示,在细绳的下端挂一物体,用力F拉物体,使细绳偏离竖直方向α角,且保持α角不变,当拉力F与水平方向夹角β为多大时,拉力F的值最小( )
A. B. C. D.
10.如图所示,晾晒衣服的绳子两端分别固定在两根竖直杆上的A、B两点,绳子的质量及绳与衣架挂钩间的摩擦均忽略不计,衣服处于静止状态.如果保持绳子A端、B端在杆上位置不变,将右侧杆平移到虚线位置,稳定后衣服仍处于静止状态.则( )
A.B端移到B1位置时,绳子张力不变
B.B端移到B2位置时,绳子张力变小
C.B端在杆上位置不动,将杆移动到虚线位置时,绳子张力变大
D.B端在杆上位置不动,将杆移动到虚线位置时,绳子张力变小
二、计算题:
1. 一个物体受三个力的作用,已知一个力是80 N,指向东偏北30°的方向;一个力为40 N,指向西北方向;一个力为20 N,指向南方,求三个力的合力大小.
2. 两人在两岸用绳拉小船在河流中行驶.如图所示,已知甲的拉力是200 N,拉力方向与航向夹角为60°,乙的拉力大小为N,且两绳在同一水平面内,若要使小船能在河流正中间沿直线行驶,乙用力的方向如何?小船受到两拉力的合力为多大?
【答案与解析】
选择题:
1.AC
解析:只有同一个物体受到的力才能合成,分别作用在不同物体上的力不能合成.合力是对原来几个分力的等效替代,两力可以是不同性质的力,但合力与分力不能同时存在.所以,正确选项为A、C.
2. B
解析:由题意知 F1+F2=A,F1-F2=B,
故,.
当两力互相垂直时,
合力
3. C
解析:以滑轮为研究对象,悬挂重物的绳的拉力是F=mg=100N,故小滑轮受到绳的作用力沿BC、BD方向,大小都是100N.从下图中可看出∠CBD=120°,∠CBE=∠DBE得∠CBE=∠DBE=60°,即△CBE是等边三角形,故100N.
4.C
解析:三力合成,若前面力的合力可与第三力大小相等,方向相反,就可以使这三力的合力为零,只要使第三力在其他两力的合力范围之内,就可能使合力为零,即第三力F3满足:|F1-F2|≤F3≤F1+F2.选项A中,前两力合力范围是:2N≤≤12N,第三力在其范围之内;选项B中,前两力合力范围是:3N≤≤7N,第三力在其合力范围之内;选项C中,前两力合力范围是:4N≤≤6N,第三力不在其合力范围之内;选项D中,前两力合力范围是:0≤≤20N,第三力在其合力范围之内,故只有C中第三力不在前两力合力范围之内,即C项中的三力合力不可能为零.
5. A
解析:两绳拉力的合力大小F与重力大小相等,故合力F不变.但由于两手间距增大,使两绳拉力的夹角增大,要使合力不变,则两绳拉力应增大,即T增大.故选项A正确.
6. A
解析:物体M受四个力作用,支持力和重力都在竖直方向上,故推力F与摩擦力的合力一定在竖直方向上,由于推力F的方向斜向下,由此可断定力F与摩擦力的合力一定竖直向下.
7. B
解析:D结点处有四根网绳,是∠dDe=∠bOg=120°,因此每根绳中承受力为F/2.注意冲击力F中已包含mg的作用效果.
8. C
解析:在小球往上移动的过程中,小球所受的重力不变,拉力F与重力的分力F1大小相等、方向相反,并且随着小球上移,F1与F2的方向均发生变化,此时力的平行四边形的形状变化规律不直观,力随角度变化的关系也难建立.而此处所求的力的变化关系是由于O′A段细线缩短引起的,因此可建立与O′A线段长之间的变化关系.如图所示,设O′A段长为L,小球半径为r,O′点到半球顶的距离为d.利用三角形相似得 .
当小球往上移动时,L减小,d、r和R都不变,因此F1减小(即F减小)、F2不变,故选项C正确.
9. C
解析:由题意知,O点所受的合力在拉力F方向变化的过程中始终为零.如下图所示,在拉力F方向变化过程中,OA绳的拉力与拉力F的合力F′总等于物体重力的大小,所以,本题转化为已知合力求分力的问题,由下图可知:拉力F方向垂直于绳的拉力时,F有最小值,此时.
10.AD
解析:挂钩相当于滑轮,轻绳两端对衣架挂钩的拉力大小相等,由平行四边形定则可知:重力的反向延长线将绳子的夹角θ平分,如图所示,设绳子长度为L,两杆之间的距离为d,由几何关系可得:.
B端上下移动时,d和L不变,夹角θ不变,绳子张力不变;杆移到虚线位置时,d减小而L不变,夹角θ变小,绳子张力变小.故选项A、D正确.
二、计算题:
1. 63.34N
解析:物体受力示意图如图所示.取向东方向为x轴正方向,向北方向为y轴正方向,建立直角坐标系,如图所示.将F1、F2进行正交分解.
由图可知
,.
,.
,.
x方向的合力为
.
y方向的合力为
.
最后三个力的合力为.
2. 400N
解析:此题可用正交分解的方法处理,要小船能在河流正中间沿直线行驶,则垂直河流方向合力应为零,则,故,而合力
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
