6.3实际问题与反比例函数 巩固练习(基础题)(含答案)
文档属性
| 名称 | 6.3实际问题与反比例函数 巩固练习(基础题)(含答案) | 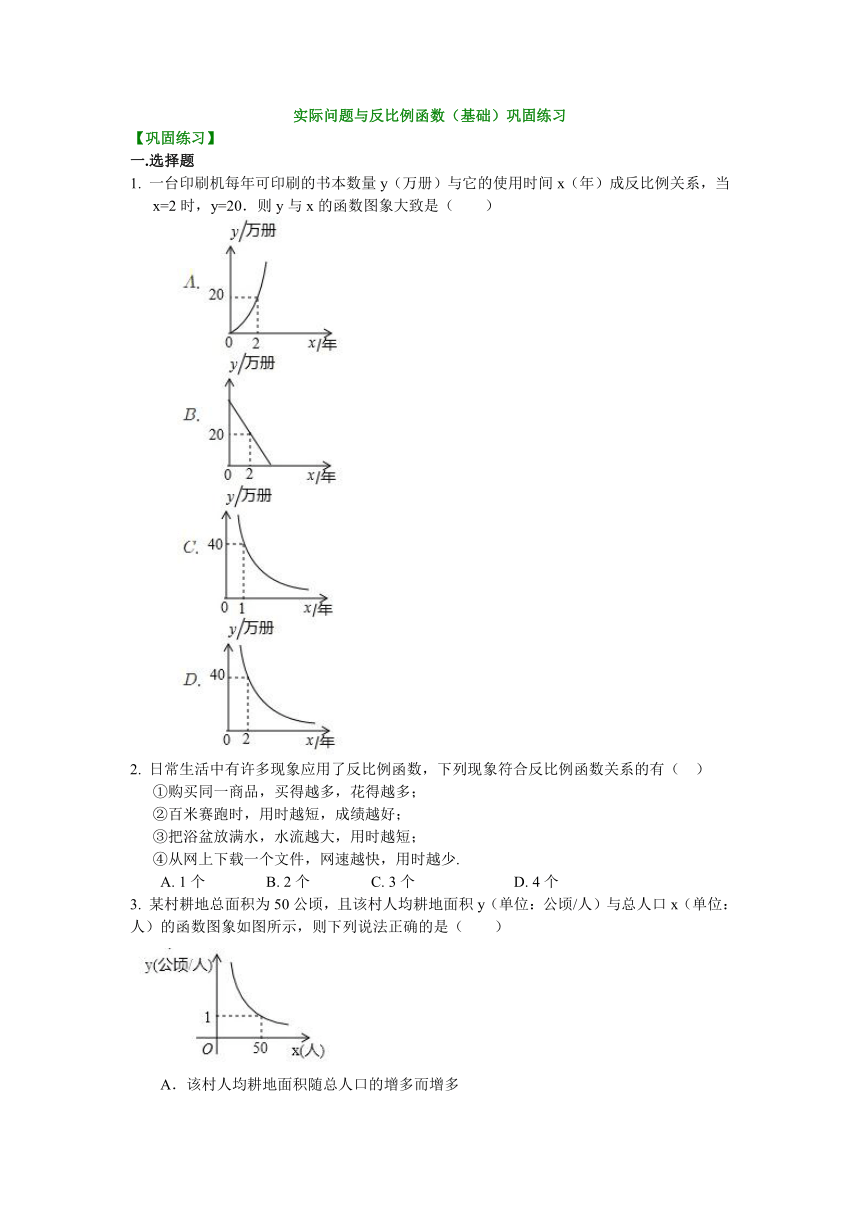 | |
| 格式 | zip | ||
| 文件大小 | 124.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-05 20:28:24 | ||
图片预览


文档简介
实际问题与反比例函数(基础)巩固练习
【巩固练习】
一.选择题
1. 一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
2. 日常生活中有许多现象应用了反比例函数,下列现象符合反比例函数关系的有( )
①购买同一商品,买得越多,花得越多;
②百米赛跑时,用时越短,成绩越好;
③把浴盆放满水,水流越大,用时越短;
④从网上下载一个文件,网速越快,用时越少.
A. 1个 B. 2个 C. 3个 D. 4个
3. 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
4. 若为圆柱底面的半径,为圆柱的高.当圆柱的侧面积一定时,则与之间函数关系的图象大致是( ).
5. 如果变阻器两端电压不变,那么通过变阻器的电流与电阻的函数关系图象大致是( )
6. 下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成100赛跑时,时间t(s)与他跑步的平均速度v()之间的关系.
B.菱形的面积为48,它的两条对角线的长为()与()的关系.
C.一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的体积V之间的关系.
D.压力为600N时,压强P与受力面积S之间的关系.
二.填空题
7.某蓄水池的排水管的平均排水量为每小时8立方米,6小时可以将满池水全部排空.现在排水量为平均每小时Q立方米,那么将满池水排空所需要的时间为t(小时),写出时间t(小时)与Q之间的函数表达式 .
8. 由电学欧姆定律知,电压不变时,电流强度I与电阻R成反比例,已知电压不变,电阻R=20时,电流强度I=0.25A.则
(1)电压U=______V; (2)I与R的函数关系式为______;
(3)当R=12.5?时的电流强度I=______A;
(4)当I=0.5A时,电阻R=______.
9. 一水桶的下底面积是桶盖面积的2倍,如果将其底朝下放在桌上,它对桌面的压强是500.翻过来放,对桌面的压强是_____________.
10.一个水池装水12,如果从水管中每小时流出的水,经过可以把水放完,那么 与的函数关系式是______,自变量的取值范围是______.
11.某种大米单价是y元/千克,若购买x千克花费了2.2元,则y与x的表达式是 .
12. 一定质量的氧气,它的密度是它的体积的反比例函数,当V=20时,,当V=40时,______.
三.解答题
13. 池内装有12的水,如果从排水管中每小时流出的水是,则经过小时就可以把水放完.
(1)求与的函数关系式,并写出自变量的取值范围;
(2)画出函数图象的草图.
14. 去学校食堂就餐,经常会在一个买菜窗口前等待.经调查发现,同学的舒适度指数y与等待时间x(分)之间存在如下的关系:,求:
(1)若等待时间x=5分钟时,求舒适度y的值;
(2)舒适度指数不低于10时,同学才会感到舒适.函数的图象如图(x>0),请根据图象说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
某机床加工一批机器零件,如果每小时加工30个,那么12小时可以完成.
(1)设每小时加工个零件,所需时间为小时,写出与之间的函数关系式,画出图象;
(2)若要在一个工作日(8小时)内完成,每小时要比原来多加工几个?
【答案与解析】
一.选择题
1. 【答案】C;
2. 【答案】C;
【解析】②③④为反比例函数,①为正比例函数.
3.【答案】D.
4.【答案】B;
【解析】侧面积一定,h,r成反比例,考虑到实际问题,选第一象限内的图象.
5.【答案】B;
【解析】应用物理学的知识:U=I×R.
6.【答案】C;
【解析】因为m=ρV,当V=30时,m=30ρ,故为正比例函数.
二.填空题
7.【答案】t=.
8.【答案】(1)5; (2); (3)0.4; (4)10.
9.【答案】1000
【解析】压强与面积的乘积是一个定值.
10.【答案】;>0;
11.【答案】;
12.【答案】0.68;
三.解答题
13.【解析】
解:(1)由已知条件,得.
(2)如图所示.
14.【解析】
解:(1)当x=5时,舒适度y=20;
(2)舒适度指数不低于10时,由图象y≥10时,0<x≤10
所以作为食堂的管理员,让每个在窗口买菜的同学最多等待10分钟.
15.【解析】
解:(1)需加工的零件数为30×12=360(个).
与之间的函数关系式为.
图象如图所示.
(2)当=8时,=360÷8=45,45-30=15.
∴ 要在8小时内完成,每小时比原来要多加工15个.
【巩固练习】
一.选择题
1. 一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
2. 日常生活中有许多现象应用了反比例函数,下列现象符合反比例函数关系的有( )
①购买同一商品,买得越多,花得越多;
②百米赛跑时,用时越短,成绩越好;
③把浴盆放满水,水流越大,用时越短;
④从网上下载一个文件,网速越快,用时越少.
A. 1个 B. 2个 C. 3个 D. 4个
3. 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
4. 若为圆柱底面的半径,为圆柱的高.当圆柱的侧面积一定时,则与之间函数关系的图象大致是( ).
5. 如果变阻器两端电压不变,那么通过变阻器的电流与电阻的函数关系图象大致是( )
6. 下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成100赛跑时,时间t(s)与他跑步的平均速度v()之间的关系.
B.菱形的面积为48,它的两条对角线的长为()与()的关系.
C.一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的体积V之间的关系.
D.压力为600N时,压强P与受力面积S之间的关系.
二.填空题
7.某蓄水池的排水管的平均排水量为每小时8立方米,6小时可以将满池水全部排空.现在排水量为平均每小时Q立方米,那么将满池水排空所需要的时间为t(小时),写出时间t(小时)与Q之间的函数表达式 .
8. 由电学欧姆定律知,电压不变时,电流强度I与电阻R成反比例,已知电压不变,电阻R=20时,电流强度I=0.25A.则
(1)电压U=______V; (2)I与R的函数关系式为______;
(3)当R=12.5?时的电流强度I=______A;
(4)当I=0.5A时,电阻R=______.
9. 一水桶的下底面积是桶盖面积的2倍,如果将其底朝下放在桌上,它对桌面的压强是500.翻过来放,对桌面的压强是_____________.
10.一个水池装水12,如果从水管中每小时流出的水,经过可以把水放完,那么 与的函数关系式是______,自变量的取值范围是______.
11.某种大米单价是y元/千克,若购买x千克花费了2.2元,则y与x的表达式是 .
12. 一定质量的氧气,它的密度是它的体积的反比例函数,当V=20时,,当V=40时,______.
三.解答题
13. 池内装有12的水,如果从排水管中每小时流出的水是,则经过小时就可以把水放完.
(1)求与的函数关系式,并写出自变量的取值范围;
(2)画出函数图象的草图.
14. 去学校食堂就餐,经常会在一个买菜窗口前等待.经调查发现,同学的舒适度指数y与等待时间x(分)之间存在如下的关系:,求:
(1)若等待时间x=5分钟时,求舒适度y的值;
(2)舒适度指数不低于10时,同学才会感到舒适.函数的图象如图(x>0),请根据图象说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
某机床加工一批机器零件,如果每小时加工30个,那么12小时可以完成.
(1)设每小时加工个零件,所需时间为小时,写出与之间的函数关系式,画出图象;
(2)若要在一个工作日(8小时)内完成,每小时要比原来多加工几个?
【答案与解析】
一.选择题
1. 【答案】C;
2. 【答案】C;
【解析】②③④为反比例函数,①为正比例函数.
3.【答案】D.
4.【答案】B;
【解析】侧面积一定,h,r成反比例,考虑到实际问题,选第一象限内的图象.
5.【答案】B;
【解析】应用物理学的知识:U=I×R.
6.【答案】C;
【解析】因为m=ρV,当V=30时,m=30ρ,故为正比例函数.
二.填空题
7.【答案】t=.
8.【答案】(1)5; (2); (3)0.4; (4)10.
9.【答案】1000
【解析】压强与面积的乘积是一个定值.
10.【答案】;>0;
11.【答案】;
12.【答案】0.68;
三.解答题
13.【解析】
解:(1)由已知条件,得.
(2)如图所示.
14.【解析】
解:(1)当x=5时,舒适度y=20;
(2)舒适度指数不低于10时,由图象y≥10时,0<x≤10
所以作为食堂的管理员,让每个在窗口买菜的同学最多等待10分钟.
15.【解析】
解:(1)需加工的零件数为30×12=360(个).
与之间的函数关系式为.
图象如图所示.
(2)当=8时,=360÷8=45,45-30=15.
∴ 要在8小时内完成,每小时比原来要多加工15个.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
