探索相似三角形相似的条件同步练习(附答案解析)
文档属性
| 名称 | 探索相似三角形相似的条件同步练习(附答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 87.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-05 22:39:50 | ||
图片预览

文档简介
探索相似三角形相似的条件
【巩固练习】
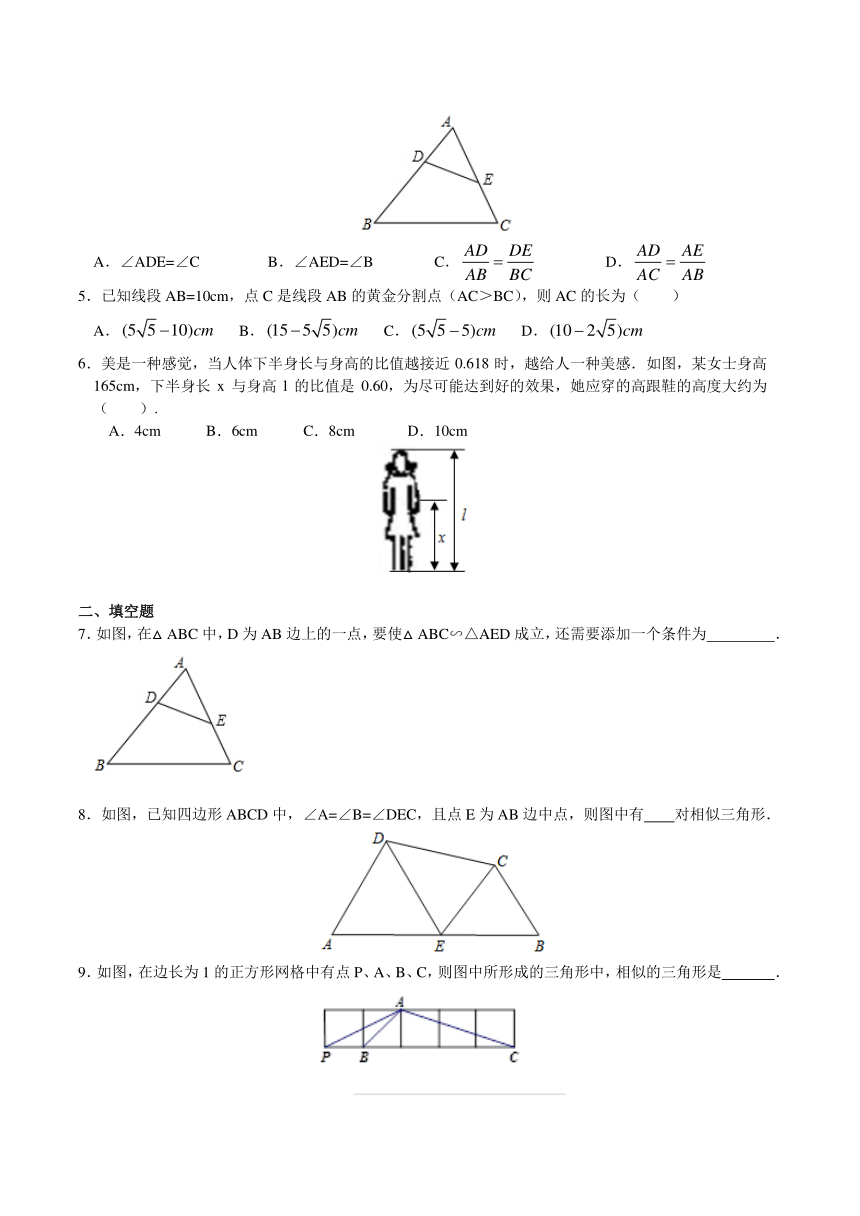
一、选择题 1.在△ABC和△A1B1C1中,下列四个命题:
(1)若AB= A1B1,AC= A1C1,∠A=∠A1,则△ABC≌△A1B1C1;
(2)若AB= A1B1,AC= A1C1,∠B=∠B1,则△ABC≌△A1B1C1;
(3)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(4)若AC:A1C1=CB:B1C1,∠C=∠C1,则△ABC∽△A1B1C1.
其中真命题的个数为( )
A.4个 B.3个 C.2个 D.1个
2.如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
3.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
A.P1 B.P2 C.P3 D.P4
4.如图,在△ABC中,如果DE与BC不平行,那么下列条件中,不能判断△ADE∽△ABC的是( )
A.∠ADE=∠C B.∠AED=∠B C. D.
5.已知线段AB=10cm,点C是线段AB的黄金分割点(AC>BC),则AC的长为( )
A. B. C. D.
6.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( ).
A.4cm B.6cm C.8cm D.10cm
二、填空题
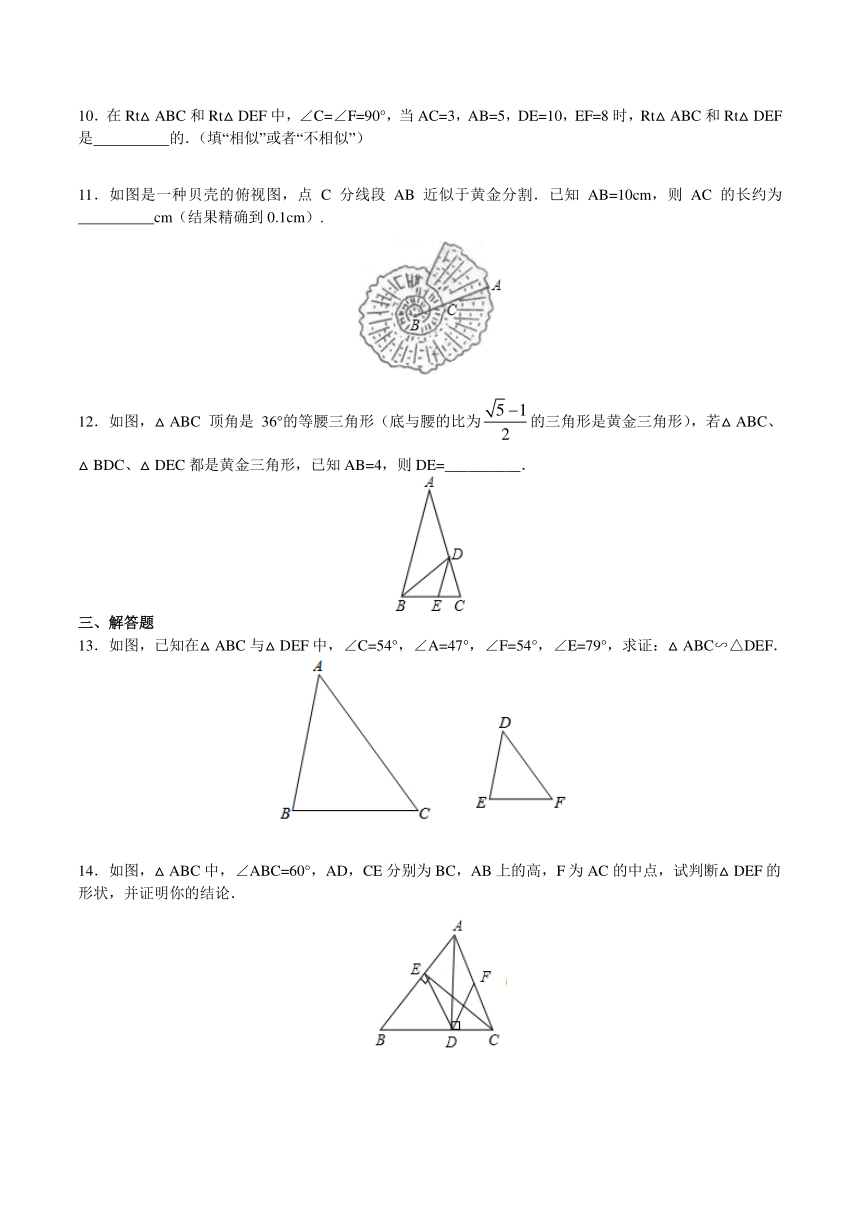
7.如图,在△ABC中,D为AB边上的一点,要使△ABC∽△AED成立,还需要添加一个条件为 .
8.如图,已知四边形ABCD中,∠A=∠B=∠DEC,且点E为AB边中点,则图中有 对相似三角形.
9.如图,在边长为1的正方形网格中有点P、A、B、C,则图中所形成的三角形中,相似的三角形是 .
10.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,当AC=3,AB=5,DE=10,EF=8时,Rt△ABC和Rt△DEF是 的.(填“相似”或者“不相似”)
11.如图是一种贝壳的俯视图,点C分线段AB近似于黄金分割.已知AB=10cm,则AC的长约为__________cm(结果精确到0.1cm).
12.如图,△ABC顶角是36°的等腰三角形(底与腰的比为的三角形是黄金三角形),若△ABC、△BDC、△DEC都是黄金三角形,已知AB=4,则DE=__________.
三、解答题
13.如图,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°,求证:△ABC∽△DEF.
14.如图,△ABC中,∠ABC=60°,AD,CE分别为BC,AB上的高,F为AC的中点,试判断△DEF的形状,并证明你的结论.
【答案与解析】
一、选择题
1.【答案】B;
【解析】解:(1)若AB=A1B1,AC=A1C1,∠A=∠A1,能用SAS定理判定△ABC≌△A1B1C1,故(1)正确;
(2)若AB=A1B1,AC=A1C1,∠B=∠B1,不能用ASS判定△ABC≌△A1B1C1,故(2)错误;
(3)若∠A=∠A1,∠C=∠C1,能判定△ABC∽△A1B1C1,故(3)正确;
(4)若AC:A1C1=CB:C1B1,∠C=∠C1,能利用两组对应边的比相等且夹角相等的两三角形相似判定△ABC∽△A1B1C1,故(4)正确.
正确的个数有3个;
故选:B.
2.【答案】B.
3.【答案】C;
4.【答案】C;
5.【答案】C.
【解析】∵点C是线段AB的黄金分割点(AC>BC), ∴AC=, 而AB=10cm,∴AC=×10=(5-5)cm.故选C.
6.【答案】C.
【解析】根据已知条件得下半身长是165×0.60=99cm, 设需要穿的高跟鞋是ycm,则根据黄金分割的定义得:=0.618, 解得:y≈8cm.故选C.
二、填空题
7.【答案】 ∠ADE=∠C 或∠AED=∠B或?.
【解析】据判定三角形相似的方法来找条件.
8.【答案】;
【解析】解:∵∠A=∠B=∠DEC,
∴∠1+∠2=∠2+∠4,
∴∠1=∠4,
又∵∠A=∠B,
∴△AED∽△BCE,
∴,
∵点E为AB边中点,
∴,
∵∠A=∠DEC,
∴△AED∽△EDC,
∴△AED∽△BCE∽△EDC,
故图中有 3对相似三角形.
故答案为:3.
9.【答案】△APB∽△CPA;
10.【答案】相似;
11.【答案】6.2或3.8.
【解析】由题意知AC:AB=BC:AC, ∴AC:AB≈0.618, ∴AC=0.618×10cm≈6.2(结果精确到0.1cm)或AC=10-6.2=3.8. 故答案为:6.2或3.8.
12.【答案】6-2.
【解析】根据题意可知,BC=AB, ∵△ABC顶角是36°的等腰三角形, ∴AB=AC,∠ABC=∠C=72°, 又∵△BDC也是黄金三角形, ∴∠CBD=36°,BC=BD, ∴∠ABD=∠ABC-∠CBD=36°=∠A, ∴BD=AD,同理可证DE=DC, ∴DE=DC=AC-AD=AB-BC=AB-AB=6-2. 故答案为:6-2.
三、解答题
13.【解析】
解:在△ABC中,∠B=180°﹣∠A﹣∠C=79°,
在△ABC和△DEF中,,
∴△ABC∽△DEF.
14.【解析】
解:连接EF,△DEF为等边三角形,由∠ABC=60°,
易得:.
∴△BDE∽△BAC,
∴,
∴DE=AC.
又∵F为中点,
∴在Rt△ADC中,DF=AC,在Rt△ACE中,EF=AC.
所以DE=DF=EF.
即:△DEF为等边三角形.
【巩固练习】
一、选择题 1.在△ABC和△A1B1C1中,下列四个命题:
(1)若AB= A1B1,AC= A1C1,∠A=∠A1,则△ABC≌△A1B1C1;
(2)若AB= A1B1,AC= A1C1,∠B=∠B1,则△ABC≌△A1B1C1;
(3)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(4)若AC:A1C1=CB:B1C1,∠C=∠C1,则△ABC∽△A1B1C1.
其中真命题的个数为( )
A.4个 B.3个 C.2个 D.1个
2.如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
3.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
A.P1 B.P2 C.P3 D.P4
4.如图,在△ABC中,如果DE与BC不平行,那么下列条件中,不能判断△ADE∽△ABC的是( )
A.∠ADE=∠C B.∠AED=∠B C. D.
5.已知线段AB=10cm,点C是线段AB的黄金分割点(AC>BC),则AC的长为( )
A. B. C. D.
6.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( ).
A.4cm B.6cm C.8cm D.10cm
二、填空题
7.如图,在△ABC中,D为AB边上的一点,要使△ABC∽△AED成立,还需要添加一个条件为 .
8.如图,已知四边形ABCD中,∠A=∠B=∠DEC,且点E为AB边中点,则图中有 对相似三角形.
9.如图,在边长为1的正方形网格中有点P、A、B、C,则图中所形成的三角形中,相似的三角形是 .
10.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,当AC=3,AB=5,DE=10,EF=8时,Rt△ABC和Rt△DEF是 的.(填“相似”或者“不相似”)
11.如图是一种贝壳的俯视图,点C分线段AB近似于黄金分割.已知AB=10cm,则AC的长约为__________cm(结果精确到0.1cm).
12.如图,△ABC顶角是36°的等腰三角形(底与腰的比为的三角形是黄金三角形),若△ABC、△BDC、△DEC都是黄金三角形,已知AB=4,则DE=__________.
三、解答题
13.如图,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°,求证:△ABC∽△DEF.
14.如图,△ABC中,∠ABC=60°,AD,CE分别为BC,AB上的高,F为AC的中点,试判断△DEF的形状,并证明你的结论.
【答案与解析】
一、选择题
1.【答案】B;
【解析】解:(1)若AB=A1B1,AC=A1C1,∠A=∠A1,能用SAS定理判定△ABC≌△A1B1C1,故(1)正确;
(2)若AB=A1B1,AC=A1C1,∠B=∠B1,不能用ASS判定△ABC≌△A1B1C1,故(2)错误;
(3)若∠A=∠A1,∠C=∠C1,能判定△ABC∽△A1B1C1,故(3)正确;
(4)若AC:A1C1=CB:C1B1,∠C=∠C1,能利用两组对应边的比相等且夹角相等的两三角形相似判定△ABC∽△A1B1C1,故(4)正确.
正确的个数有3个;
故选:B.
2.【答案】B.
3.【答案】C;
4.【答案】C;
5.【答案】C.
【解析】∵点C是线段AB的黄金分割点(AC>BC), ∴AC=, 而AB=10cm,∴AC=×10=(5-5)cm.故选C.
6.【答案】C.
【解析】根据已知条件得下半身长是165×0.60=99cm, 设需要穿的高跟鞋是ycm,则根据黄金分割的定义得:=0.618, 解得:y≈8cm.故选C.
二、填空题
7.【答案】 ∠ADE=∠C 或∠AED=∠B或?.
【解析】据判定三角形相似的方法来找条件.
8.【答案】;
【解析】解:∵∠A=∠B=∠DEC,
∴∠1+∠2=∠2+∠4,
∴∠1=∠4,
又∵∠A=∠B,
∴△AED∽△BCE,
∴,
∵点E为AB边中点,
∴,
∵∠A=∠DEC,
∴△AED∽△EDC,
∴△AED∽△BCE∽△EDC,
故图中有 3对相似三角形.
故答案为:3.
9.【答案】△APB∽△CPA;
10.【答案】相似;
11.【答案】6.2或3.8.
【解析】由题意知AC:AB=BC:AC, ∴AC:AB≈0.618, ∴AC=0.618×10cm≈6.2(结果精确到0.1cm)或AC=10-6.2=3.8. 故答案为:6.2或3.8.
12.【答案】6-2.
【解析】根据题意可知,BC=AB, ∵△ABC顶角是36°的等腰三角形, ∴AB=AC,∠ABC=∠C=72°, 又∵△BDC也是黄金三角形, ∴∠CBD=36°,BC=BD, ∴∠ABD=∠ABC-∠CBD=36°=∠A, ∴BD=AD,同理可证DE=DC, ∴DE=DC=AC-AD=AB-BC=AB-AB=6-2. 故答案为:6-2.
三、解答题
13.【解析】
解:在△ABC中,∠B=180°﹣∠A﹣∠C=79°,
在△ABC和△DEF中,,
∴△ABC∽△DEF.
14.【解析】
解:连接EF,△DEF为等边三角形,由∠ABC=60°,
易得:.
∴△BDE∽△BAC,
∴,
∴DE=AC.
又∵F为中点,
∴在Rt△ADC中,DF=AC,在Rt△ACE中,EF=AC.
所以DE=DF=EF.
即:△DEF为等边三角形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
