物理:第3章《抛体运动》课件(鲁科版必修2)
文档属性
| 名称 | 物理:第3章《抛体运动》课件(鲁科版必修2) |  | |
| 格式 | rar | ||
| 文件大小 | 229.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2010-07-28 20:37:00 | ||
图片预览





文档简介
课件12张PPT。zxxk精品课件第三章 抛体运动1曲线运动①做曲线运动的条件:合外力方向与初速度方向不在一条直线上②曲线运动的速度方向:该点切线方向③曲线运动是变速运动2运动的合成与分解①合运动:②分运动:物体实际的运动参与实际运动的两个运动④运动的合成与分解遵循平行边形定则
(运动的分解常按正交分解法)③合运动与分运动具有等时性
两个分运动具有独立性问题:已知两个分运动,则合运动是什么运动?
(从合速度、合加速度的方向和大小讨论)zxxk精品课件3小船过河:①过河时间要最短:船身一定垂直对岸。②要最短距离过河:船身应向上游4、竖直上抛运动①特点:初速度V0向上,只受重力作用②运动规律:a :上升过程:做初速度V0,加速度为g的匀减速运动b :下降过程:做初速度0,加速度为g的匀加速运动c :上升过程与下降过程是对称的(即上升时间与下降
到抛出点的时间相等,落回到抛出点的速度大小与抛
出点速度大小相等,方向相反。若规定向上为正方向,则它是以初速度为V0,加速度为g的匀减速直线运动。zxxk精品课件5竖直下抛运动:
初速度为v0向下,加速度为g的匀加速运动。6、平抛运动:①运动特点:
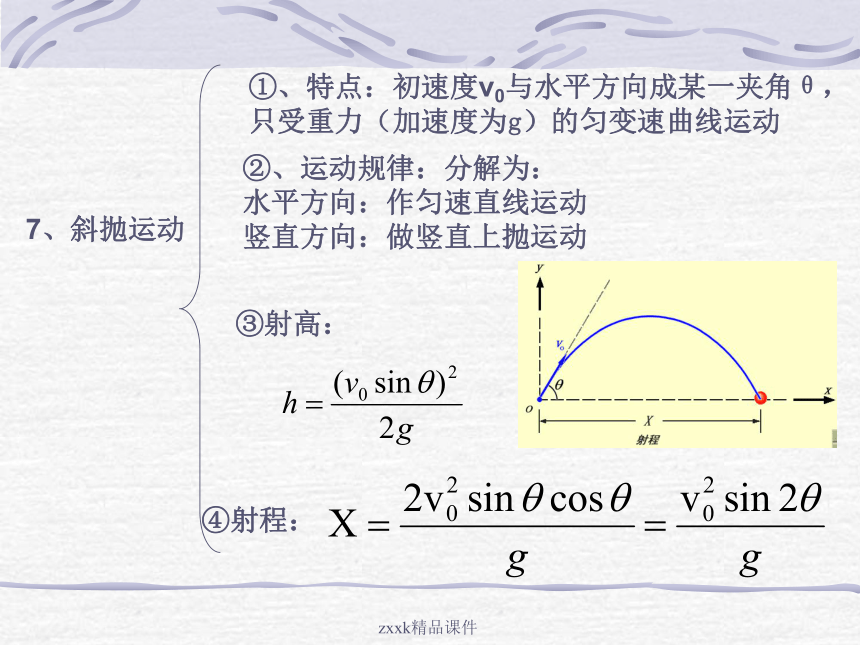
初速度v0水平,加速度为g的匀变速曲线运动。②运动规律:水平方向:做初速度为v0的匀速直线运动:竖直方向:做自由落体运动zxxk精品课件7、斜抛运动①、特点:初速度v0与水平方向成某一夹角θ,
只受重力(加速度为g)的匀变速曲线运动②、运动规律:分解为:
水平方向:作匀速直线运动
竖直方向:做竖直上抛运动③射高:④射程:zxxk精品课件8、实验:1、运动的独立性 P48页2研究平抛运动P55页3、探究射高和射程与初速度和抛射角的关系P60页独立性平抛运动zxxk精品课件1、北京时间2004年8月15日凌晨,在郭晶晶和吴敏霞为中国
获得一枚奥运会跳水金牌之后,中国选手田亮和杨景辉在男
子双人10米跳台项目上力压群雄再次为中国代表团获得一枚
金牌。设田亮从离水面10米高的平台上向上跃起,举双臂直
体离开台面,此时其重心位于从手到脚全长的中点,跃起后
重心升高0.45米达到最高点,落水时身体竖直,手先入水(
在此过程中运动员水平方向的运动忽略不计),如图所示,
从离开跳台至手触水面,田亮可用于完成空中动作的时间
是_______s.(计算时,可以把运动员看做全部质量集中
在重心的一个质点,g取10m/s2,结果保留两位有效数字)解:根据题意知田亮在跳水做动作过程中做自由落体运动,则有:所以完成空中动作的时间zxxk精品课件2:宇航员站在一星球表面的某高处,沿水平方向抛出一个
小球,小球落到星球表面,测得抛出点与落地点之间的距离
为L。若抛出时的初速度增大到2倍,则抛出点与落地点之间
的距离为 ,如图3所示。已知小球飞行时间为t,且两落地
点在同一水平面上。求:
(1)该星球表面的重力加速度的数值。
(2)已知该星球半径为R,万有引力常数为G,求该星球的质量M 解(1)设抛出点高度为h,初速度为v0,
星球表面重力加速度为g星。
由题意 得: 由上式解得(2)设在星球的表面放一质量
为m的物体,则有:所以该星球的质量zxxk精品课件3:如图4所示,一个同学做平抛实验时,只在纸上记下过起
点的纵坐标y方向,但未记录平抛运动的起点,并描下了平抛
运动的一段轨迹,在轨迹上取A、B两点,用刻度尺分别测量
出它们到y轴的距离x1、x2以及AB的竖直距离h,则小球平
抛运动的初速度是多少?解:依题意:设从抛出点到A、B的竖直高度分别为hA和hB。
平抛点到A、B的时间为tA和 tB,则有: 由方程(1)(2)(3)解得:
小球的初速度zxxk精品课件4、斜上抛出一球,抛射角α=600,当t=1s时,球仍斜向
上升,但方向已跟水平方向成β=450角,不计空阻力。求:
(结果保留三位有效字)
(1)球的初速度是多少?
(2)球将在什么时候达到最高点?(g=10m/s2)解(1)依题意,设初速度为v0 ,则有:由方程(1)(2)(3)解得(2)设小球从抛出到最高点时间为 t1所以有:zxxk精品课件5、如图,光滑斜面长为a,宽为b,倾角为θ,一小物体从
斜面上方的左端顶点P水平射入,恰能从右下方的端点Q离开
斜面,试求其入射的初速度V0解:依题意得小物体做类似平抛运动:
即:以加速度为的类似平抛运动,所以有:解方程(1)(2)得小物体入射的初速度
zxxk精品课件6一家用水泵的出水管是水平,喷出的水,测得其水平射程
为0.8m,管口距地面1.25m,水管口的横截面积S=1.2×10-2m2,
求水管出水的流量Q(即每秒喷出水的质量,取g=10m/s2)解:依题意得:设水从管口流到地面的时间为t,
则有:所以由(1)(2)(3)解得
流量zxxk精品课件1.实验:让橡皮从桌子上水平抛出,如何得出其初速度? 2.在实际生产和生活中,我们往往关注斜抛物体的最在
高度和从抛出点到落地点的水平距离,那么这两者的
大小与哪些因素有关呢?例如消防上救火,我们如何
有效地使水抛得更高更远呢?
(运动的分解常按正交分解法)③合运动与分运动具有等时性
两个分运动具有独立性问题:已知两个分运动,则合运动是什么运动?
(从合速度、合加速度的方向和大小讨论)zxxk精品课件3小船过河:①过河时间要最短:船身一定垂直对岸。②要最短距离过河:船身应向上游4、竖直上抛运动①特点:初速度V0向上,只受重力作用②运动规律:a :上升过程:做初速度V0,加速度为g的匀减速运动b :下降过程:做初速度0,加速度为g的匀加速运动c :上升过程与下降过程是对称的(即上升时间与下降
到抛出点的时间相等,落回到抛出点的速度大小与抛
出点速度大小相等,方向相反。若规定向上为正方向,则它是以初速度为V0,加速度为g的匀减速直线运动。zxxk精品课件5竖直下抛运动:
初速度为v0向下,加速度为g的匀加速运动。6、平抛运动:①运动特点:
初速度v0水平,加速度为g的匀变速曲线运动。②运动规律:水平方向:做初速度为v0的匀速直线运动:竖直方向:做自由落体运动zxxk精品课件7、斜抛运动①、特点:初速度v0与水平方向成某一夹角θ,
只受重力(加速度为g)的匀变速曲线运动②、运动规律:分解为:
水平方向:作匀速直线运动
竖直方向:做竖直上抛运动③射高:④射程:zxxk精品课件8、实验:1、运动的独立性 P48页2研究平抛运动P55页3、探究射高和射程与初速度和抛射角的关系P60页独立性平抛运动zxxk精品课件1、北京时间2004年8月15日凌晨,在郭晶晶和吴敏霞为中国
获得一枚奥运会跳水金牌之后,中国选手田亮和杨景辉在男
子双人10米跳台项目上力压群雄再次为中国代表团获得一枚
金牌。设田亮从离水面10米高的平台上向上跃起,举双臂直
体离开台面,此时其重心位于从手到脚全长的中点,跃起后
重心升高0.45米达到最高点,落水时身体竖直,手先入水(
在此过程中运动员水平方向的运动忽略不计),如图所示,
从离开跳台至手触水面,田亮可用于完成空中动作的时间
是_______s.(计算时,可以把运动员看做全部质量集中
在重心的一个质点,g取10m/s2,结果保留两位有效数字)解:根据题意知田亮在跳水做动作过程中做自由落体运动,则有:所以完成空中动作的时间zxxk精品课件2:宇航员站在一星球表面的某高处,沿水平方向抛出一个
小球,小球落到星球表面,测得抛出点与落地点之间的距离
为L。若抛出时的初速度增大到2倍,则抛出点与落地点之间
的距离为 ,如图3所示。已知小球飞行时间为t,且两落地
点在同一水平面上。求:
(1)该星球表面的重力加速度的数值。
(2)已知该星球半径为R,万有引力常数为G,求该星球的质量M 解(1)设抛出点高度为h,初速度为v0,
星球表面重力加速度为g星。
由题意 得: 由上式解得(2)设在星球的表面放一质量
为m的物体,则有:所以该星球的质量zxxk精品课件3:如图4所示,一个同学做平抛实验时,只在纸上记下过起
点的纵坐标y方向,但未记录平抛运动的起点,并描下了平抛
运动的一段轨迹,在轨迹上取A、B两点,用刻度尺分别测量
出它们到y轴的距离x1、x2以及AB的竖直距离h,则小球平
抛运动的初速度是多少?解:依题意:设从抛出点到A、B的竖直高度分别为hA和hB。
平抛点到A、B的时间为tA和 tB,则有: 由方程(1)(2)(3)解得:
小球的初速度zxxk精品课件4、斜上抛出一球,抛射角α=600,当t=1s时,球仍斜向
上升,但方向已跟水平方向成β=450角,不计空阻力。求:
(结果保留三位有效字)
(1)球的初速度是多少?
(2)球将在什么时候达到最高点?(g=10m/s2)解(1)依题意,设初速度为v0 ,则有:由方程(1)(2)(3)解得(2)设小球从抛出到最高点时间为 t1所以有:zxxk精品课件5、如图,光滑斜面长为a,宽为b,倾角为θ,一小物体从
斜面上方的左端顶点P水平射入,恰能从右下方的端点Q离开
斜面,试求其入射的初速度V0解:依题意得小物体做类似平抛运动:
即:以加速度为的类似平抛运动,所以有:解方程(1)(2)得小物体入射的初速度
zxxk精品课件6一家用水泵的出水管是水平,喷出的水,测得其水平射程
为0.8m,管口距地面1.25m,水管口的横截面积S=1.2×10-2m2,
求水管出水的流量Q(即每秒喷出水的质量,取g=10m/s2)解:依题意得:设水从管口流到地面的时间为t,
则有:所以由(1)(2)(3)解得
流量zxxk精品课件1.实验:让橡皮从桌子上水平抛出,如何得出其初速度? 2.在实际生产和生活中,我们往往关注斜抛物体的最在
高度和从抛出点到落地点的水平距离,那么这两者的
大小与哪些因素有关呢?例如消防上救火,我们如何
有效地使水抛得更高更远呢?
同课章节目录
- 第1章 功和功率
- 导入 神奇的机械
- 第1节 机械功
- 第2节 功和能
- 第3节 功率
- 第4节 人与机械
- 第2章 能的转化与守恒
- 导入 从水车到核电站
- 第1节 动能的改变
- 第2节 势能的改变
- 第3节 能量守恒定律
- 第4节 能源与可持续发展
- 第3章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 竖直方向上的抛体运动
- 第3节 平抛运动
- 第4节 斜抛运动
- 第4章 匀速圆周运动
- 导入 身边的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 向心力与向心加速度
- 第3节 向心力的实例分析
- 第4节 离心运动
- 第5章 万有引力定律及其应用
- 导入 从嫦娥奔月到“阿波罗”上天
- 第1节 万有引力定律及引力常量的测定
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈追求
- 第6章 相对论与量子论初步
- 导入 迈入新世界
- 第1节 高速世界
- 第2节 量子世界
