江苏省南京市2019届高三9月学情调研考试数学试题
文档属性
| 名称 | 江苏省南京市2019届高三9月学情调研考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-06 15:10:24 | ||
图片预览




文档简介
南京市 2019 届高三年级学情调研
数 学 2018 .09
参考公式:
柱体的体积公式:V=Sh,其中 S 为柱体的底面积,h 为柱体的高.
一、填空题:本大题共 14 小题,每小题 5 分,共 70 分.请把答案填写在答题卡相应位置.......
上.
1. 已知集合 ? ?A= |1 5x x x R?< < , , ? ?B= | 2x x n Z? ?,n ,那么集合 A B? 中有______个元
素.
【答案】2
??2,4A B ?∩ ,共有 2 个元素
解析:本题考查了集合中交集的运算.
2. 复数 z (1 )(2 )bi i? ? ? ,其中 b R? , i 为虚数单位 .若 z 是纯虚数,则实数 b 的值为
_________.
【答案】-2
? ?? ? ? ?1 2 2 2 1z bi i b b i? ? ? ? ? ? ? ,
∵ z 是纯虚数,∴ 2 0b? ? ,∴ 2b ? ?
解析:本题考查了复数的计算.
3. 已知某地连续 5 天的最低气温(单位:摄氏度)依次是 18,21,22,24,25,那么这组
数据的方差为_________.
【答案】6
S 2 =
1
5
? 18- 22( )
2
+ 21-22( )
2
+ 22- 22( )
2
+ 24-22( )
2
+ 25-22( )
2é
?ê
ù
?ú
= 6
解析:本题考查了方差的计算.
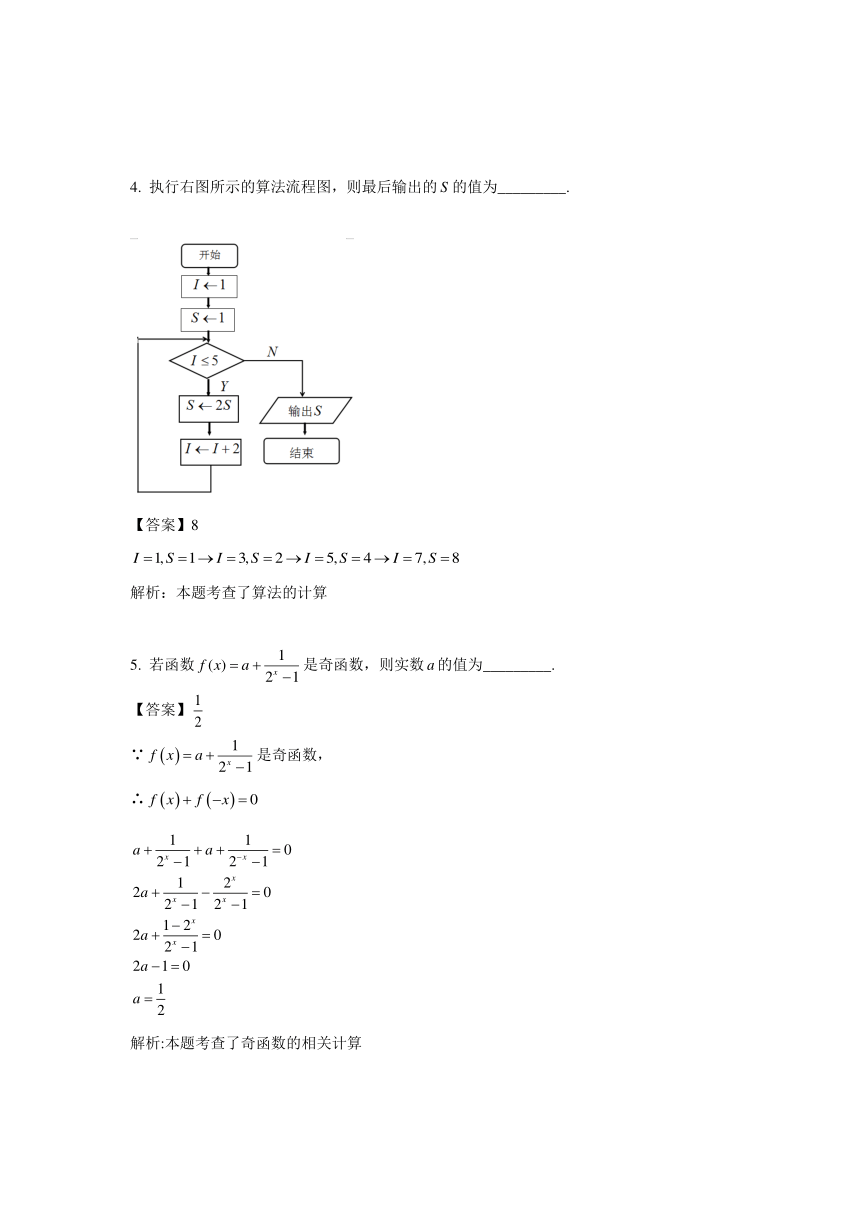
4. 执行右图所示的算法流程图,则最后输出的 S 的值为_________.
【答案】8
1, 1 3, 2 5, 4 7, 8I S I S I S I S? ? ? ? ? ? ? ? ? ? ?
解析:本题考查了算法的计算
5. 若函数
1
( )
2 1x
f x a? ?
?
是奇函数,则实数 a的值为_________.
【答案】
1
2
∵ ? ?
1
2 1x
f x a? ?
?
是奇函数,
∴ ? ? ? ? 0f x f x? ? ?
1 1
0
2 1 2 1
1 2
2 0
2 1 2 1
1 2
2 0
2 1
2 1 0
1
2
x x
x
x x
x
x
a a
a
a
a
a
?
? ? ? ?
? ?
? ? ?
? ?
?
? ?
?
? ?
?
解析:本题考查了奇函数的相关计算
6. 在平面直角坐标系 xOy 中,若抛物线 2 4y x? 的准线与双曲线
2 2
2 2
1( 0 0
x y
a b
a b
? ? > , > )的
一条渐近线的交点的纵坐标为 2,则该双曲线的离心率是__________.
【答案】 5
抛物线 2 4y x? 的准线是 1x ? ? ,∴双曲线的渐近线过 ? ?1,2? ,
∴渐近线是 2y x? ? ,∴ 2
b
a
? ∴离心率
2
21 1 2 5
c b
e
a a
? ?
? ? ? ? ? ?? ?
? ?
解析:本题考查了抛物线和双曲线的相关性质
7. 不透明的盒子中有大小、形状和质地都相同的 5 只球,其中 2 只白球,3 只红球,现从中
随机取出 2 只球,则取出的这 2 只球颜色相同的概率是________.
【答案】
2
5
解析:考察了简单概率的求解,基础题
8. 已知函数 ( ) 2sin(2 )( )
2 2
f x x
? ?
? ?? ? ? < < 的图像关于直线
6
x
?
? 对称,则 ? ?0f 的值为
________.
【答案】
f (0) = 1
因为关于
x =
p
6
对称,所以
f (x) = ±2,即
sin(
p
3
+j) = ±1,
p
3
+j =
p
2
+ kp (k ?Z),
所以
j =
p
6
+ kp (k ?Z),因为
j ?(-
p
2
,
p
2
),所以
j =
p
6
.
f (0) = 1
解析:考察了正弦函数的对称轴问题,基础题
9. 如图,在三棱柱
1 1 1ABC A B C? 中, =2AB , 1=3AA ,则四棱锥 1 1 1-A B C CB的体积是_______.
【答案】 2 3
四棱锥高为 h = 3,
V =
1
3
? 2 ? 3? 3 = 2 3.
解析:考察了空间集合体的体积,基础题
10. 在数列? ?na 中,已知 1 1a ? , 1
1
( 1)
n na a
n n
? ? ?
?
*( )n N? ,则 10a 的值为____________.
【答案】
19
10
? ? ? ? ? ?10 10 9 9 8 2 1 1a a a a a a a a? ? ? ? ? ? ? ?L L
1 1 1 1 1 1 19
1 1 1 1
9 10 8 9 2 10 10
? ? ? ? ? ? ? ? ? ? ? ?L L
解析:中档题,考察数列累加法
11. 已知 ABC? 的面积为3 15 ,且 2AC AB? ? ,
1
cos
4
A ? ? ,则 BC 的长为___________.
【答案】8
∵
1
cos
4
A ? ? , ? ?0,A ??
∴
15
sin
4
A ?
∵
1
sin 3 15
2
ABCS bc A? ? ?
∴ 24bc ?
又 2b c? ?
∴ ? ?
22 2 2 25 52 cos 2 24 64
2 2
a b c bc A b c bc? ? ? ? ? ? ? ? ? ?
∴ 8BC ?
解析:中档题,考察解三角形的相关知识
12. 在菱形 ABCD中, 60ABC ?? ? ,E 为边 BC 上一点,且 , ,则
的值为_________.
【答案】
9
2
?
设 ,
则
∴ 2 9a ?
∴
解析:中档题,考察向量的基本运算
13. 在平面直角坐标系 xOy 中,已知点 (1,1)A , (1, 1)B ? ,点 P 为圆 2 2( 4) 4x y? ? ? 上任意一
点,记 OAP? 和 OBP? 的面积分别为
1S 和 2S ,则
1
2
S
S
的最小值是_________.
【答案】 32 ?
解析:设点 ? ??? sin2,cos24?P , xylxyl OBOA ??? :,:
2
sin2cos24
2
2
1
1
???
???S 同理
2
sin2cos24
2
2
1
2
?? ??
???S
则 ?
??
??
?
??
??
sin2cos24
sin2cos24
2
1
S
S
4 2 2 sin 2 sin
4 4
4 2 2 cos 2 cos
4 4
? ?
? ?
? ?
? ?
? ? ? ?
? ? ? ?? ? ? ?
? ? ? ?
?
? ? ? ?
? ? ? ?? ? ? ?
? ? ? ?
设点 ? ?2,2 ??M ,点 cos ,sin
4 4
N
? ?
? ?
? ?? ? ? ?
? ?? ?? ? ? ?
? ? ? ?? ?
可知点 N 落在单位圆上
问题可转化为点M 和点 N 构成直线斜率绝对值的最小值
设直线 ? ?22 ??? xky 与单位圆相切
得 32??k 得最小值为 32 ?
14. 若函数 2
1
( ) 1
2
xf x ax e? ? ? 在 1x x? 和 2x x? 两处取到极值,且
2
1
2
x
x
? ,则实数 a 的取值
范围是___________.
【答案】 ?
?
?
?
?
?
??,
2ln
2
解析:函数 ? ?f x 求导得 ? ?' xf x ax e? ?
由题知有① 1
1
x
ax e? ,② 22
x
ax e? ,
②
①
: 2 12
1
x xx
e
x
?
? ,
令 ? ?2
1
2
x
t t
x
? ? ,则有 1 1tx xe t? ? ,得
1
ln
1
t
x
t
?
?
令 ? ?
ln
1
t
f t
t
?
?
, ? ?
? ?
'
2
1
1 ln
1
t
tf t
t
? ?
?
?
,
再令 ? ?
1
1 lng t t
t
? ? ? , ? ?'
2
1 t
g t
t
?
? ,又因 2t ? ,则 ? ?g t 在 ? ?2,?? 为减函数,
? ?
max
1
ln 2 0
2
g t ? ? < ,则 ? ?' 0f t < , ? ? ? ?
max
2 ln 2f t f? ?
则有
1 ln 2x ? 。由①得
1
1
x
e
a
x
? ,令 ? ? ? ?
? ?11 1'
1 1 2
1 1
1
,F
xx e xe
F x x
x x
?
? ? ,
则 ? ?1F x 在 ? ?0,1 2n 为减函数, ? ? ? ?1 min
2
ln 2
ln 2
F x F? ? ,
则
2
ln 2
a ? , a的取值范围是
2
,
ln 2
? ?
????
? ?
。
二、解答题:本大题共 6 小题,共计 90 分.请在答题卡指定区域内........作答,解答时应写出文
字说明、证明过程或演算步骤.
15.(本小题满分 14 分)
如图,已知四边形 ABCD是矩形,平面 ABCD ?平面BCE , ECBC ? , F 是BE 的中点。
(1)求证:DE //平面 ACF ;
(2)求证:平面 AFC ?平面 ABE .
【解析 】 (1)连接 BD交 AC 于点G ,连接 FG
F 、G 分别为 BE 、 BD的中点
/ /FG DE?
平面 ACF
DE ?平面 ACF
/ /DE? 平面 ACF .
(2) , F 为 BE 中点,
CF BE? ?
平面 ABCD ?平面 BCE
平面 ABCD ∩平面 BCE = BC
又 平面 ABCD, AB BC?
AB? ?平面 BCE
平面 BCE
AB CF? ?
平面 ABE, BE ?平面 ABE,
AB∩BE = B
CF? ?平面 ABE
平面 AFC
?平面 AFC ?平面 ABE .
16.(本小题满分 14 分)
已知 ??, 为钝角,且
5
3
sin ?? ,
5
3
2cos ??? .
(1)求 ?tan 的值;
(2)求 ? ??? ?2cos 的值.
【解析】
(1)
5
3
sincos
sincos
sincos2cos
22
22
22 ??
?
?
???
??
??
???
4tan2 ?? ? 2tan ??? ?
(2)
? ? ?????? sin2sincos2cos2cos ???
25
7
2cos ??
, 25
24
2sin ???
5
5
cos,
5
52
sin ??? ??
? ??? ??2cos 125
541
17.(本小题满分 14 分)
销售甲种商品所得利润是P 万元,它与投入资金 t 万元的关系有经验公式
1?
?
t
at
P ;销售乙
种商品所得利润是Q万元,它与投入资金 t 万元的关系有经验公式 btQ ? ,其中 ba, 为常数.
现将 3 万元全部投入甲、乙两种商品的销售:若全部投入甲种商品,所得利润为
4
9
万元;
若全部投入乙种商品,所得利润为 1 万元.若将 3 万元资金中的 x 万元投入甲种商品的销售,
余下的投入乙种商品的销售,则所得利润总和为 )(xf 万元.
(1)求函数 )(xf 的解析式;
(2)怎样将 3 万元资金分配给甲、乙两种商品,才能使所得利润总和最大,并求出最大值.
【解析】(1)由已知
??
?
?
?
?
?
?
??
?
?
?
?
?
3
1
3
13
4
9
4
3
b
a
b
a
]3,0[),
1
9
(
3
1
4)3(
3
1
1
3
)( ?
?
?????
?
?? x
x
xx
x
x
xf
(2) 51
1
9
1
1
9
??
?
???
?
?
x
x
x
x? ,当且仅当 ""2
1
1
1 ??
?
?? 时取,即x
x
x
3
7
3
5
4)( ???? xf
答:投资甲 2 万元,乙 1 万元时,利润总和最大,为
3
7
万元
18.(本小题满分 16 分)
在平面直角坐标系 xOy中,椭圆 E :
x2
a2
+
y2
b2
= 1 a > b > 0( )的离心率为 2
2
,且直线 l : x = 2
被椭圆 E截得的弦长为 2,与坐标轴不垂直的直线交椭圆 E于 P,Q两点,且 PQ的中点 R在
直线 l上.点 M 1,0( ).
(1)求椭圆 E的方程;
(2)求证: MR ^ PQ
【解析】(1)椭圆过点 ? ?2,1
2
2
2 2
2
62
4 1 3
1
c
e
aa
b
a b
?
? ?? ? ?? ?
?? ?
??? ?? ?
??
椭圆方程为
2 2
1
6 3
x y
? ?
(2)Q直线 l 于坐标轴不垂直
?斜率存在
设 ? ? ? ?1 1 2 2, , ,P x y Q x y
? ?? ? ? ?? ?
2 2
1 1
1 2 1 2 1 2 1 2
2 2
2 2
1
6 3
0
6 3
1
6 3
x y
x x x x y y y y
x y
?
? ?? ? ? ? ??
? ? ??
? ? ?
??
? ?
1 2 1 2
1 2 1 22
y y x x
x x y y
? ?
? ? ?
? ?
为 PQ重点,且落在直线上
1 2
1 2
4
2
PQ
x x
k
y y
? ? ?
? ? ?
?
1 2
2
MR
y y
k
?
? ?
1PQ MRk k MR PQ? ? ? ? ? ?
19.(本小题满分 16 分)
已知函数 f x( ) = ln x,g x( ) = x2
(1) 求过原点 0,0( ),且与函数 f x( )的图像相切的直线 l的方程;
(2) 若 a > 0,求函数j x( ) = g x( )- 2a2 f x( ) 在区间 1,+?é? )上的最小值.
【解析】(1)设切点坐标 ? ?0 0, lnx x , ? ?
1
f x
x
? ? ,
设切线方程: ? ?0 0
0
1
lny x x x
x
? ? ? ,代入 ? ?0,0 ,得 0x e?
即切线方程为
1
y x
e
?
(2)设 ? ? ? ? ? ?22h x g x a f x? ? = 2 22 lnx a x?
? ?
? ?? ?2 22
2 =
x a x aa
h x x
x x
? ?
? ? ?
令 ? ?=0h x? 得, x a? (负值舍)
当 0 1a? ? 时, ? ? 0h x? ? 在 ? ?1,?? 上恒成立,所以函数 ? ?h x 单调递增,
? ? ? ?min 1 1 0h x h? ? ?
所以 ? ?min 1x? ?
当 1a ? 时,可得 ? ?h x 在 ? ?1,a 上单调递减,在 ? ?,a ?? 上单调递增,
故 ? ? ? ? ? ?2 2 2min 2 ln 1 2lnh x h a a a a a a? ? ? ? ?
1 o当1 2ln 0a? ? ,即 a e? 时, ? ? ? ?2min 1 2lnx a a? ? ?
2 o当1 2ln 0a? ? ,即 a e? 时,又 ? ?1 1 0? ? ? ,所以 ? ?min 0x? ?
综上所述,
当 0 1a? ? 时, ? ?min 1x? ? ;
当1 a e? ? 时, ? ? ? ?2min 1 2lnx a a? ? ? ;
当 a e? 时, ? ?min 0x? ? .
20.(本小题满分 16 分)
如果数列 an{ }共有 k k ?N
*,k ? 4( )项,且满足条件:
则称数列 an{ }为 P k( )数列.
(1)若等比数列 an{ }为 P 4( )数列,求 a1的值;
(2)已知 m为给定的正整数,且m ? 2
①若公差为正数的等差数列 an{ }是 P 2m+ 3( )数列,求数列 an{ }的公差
②若 a
n
=
qn-1
3
,1? n ? m,n ?N *
m - n
12
,m+1? n ? 2m,n?N *
ì
í
??
?
?
?
,其中 q为常数, q < -1判断数列 an{ }是否为
P 2m( )数列,说明理由.
【解析】(1)当公比为 1 时明显不符合
当公比不为 1 时,
a
1
+ a
2
+ a
3
+ a
4
=
a
1
(1- q4 )
1- q
= 0,得到
q = -1
a
1
+ a
2
+ a
3
+ a
4
= 4 a
1
=1
所以
a
1
= ±
1
4
(2)①
a
n{ }为等差数列
a
1
+ a
2
+×××+ a
2m+3
= (2m+3)a
m+2
= 0
所以
a
m+2
= 0
因为 d > 0
则
a
1
+ a
2
+×××+ a
2m+3
= -a
1
- a
2
- a
m+1
+0+ a
m+3
+×××+ a
2m+3
= (m+2)(m+1)d =1
化简得
d =
1
(m+ 2)(m+1)
②令 2 1 2 2
1 ( 1)
0
3(1 ) 24
m
m m
q m m
S a a a
q
? ?
? ? ? ?? ? ? ? ? ?
?
得
1- qm =
(1- q)m(m+1)
8
令 2 1 2 2
1 ( ) ( 1)
1
3(1 ) 24
m
m m
q m m
T a a a
q
? ? ?
? ? ? ?? ? ? ? ? ?
?
得
1- (-q)m =
(24- m(m+1))(1+ q)
8
当 m为偶数时
(1-q)m(m+1)
8
=
(24- m(m+1))(1+q)
8
化简得
m2 + m =12(1+q)
因为
q < -1,m ? 2,所以不存在 m,
q使得等式成立
当 m为奇数时
2 =
(1- q)m(m+1)
8
+
(24- m(m+1))(1+q)
8
化简得
m2 + m-12 =
4
q
因为
q < -1,m ? 2
m
2 + m-12 < 0, -4 < m< 3
所以不存在 m,
q使得等式成立
综上,
a
n{ }不可能是 P(2m)数列
南京市 2019 届高三年级学情调研卷
数学附加题 2018.09
注意事项:
1.附加题供选修物理的考生使用.
2.本试卷共 40 分,考试时间 30 分钟.
3.答题前,考生务必将自己的姓名、学校写在答题卡上.试题的答案写在答题卡...上对
应题目的答案空格内.考试结束后,交回答题卡.
21.【选做题】在 A、B、C、D 四小题中只能选做 2 题,每小题 10 分,共计 20 分.请在答.
卷卡指定区域内.......作答.解答应写出文字说明、证明过程或演算步骤.
A.选修 4—2:矩阵与变换
已知矩阵
31
22
?
?
?A ,向量 ?
?
?
?
?
??
?
2
4
? .
(1)若向量 ?
?
?
?
?
?
?
y
x
? 满足 ?? ?A ,求 yx, 的值;
(2)求 1?A .
(1) ?
?
?
?
?
??
??
?
?
?
?
?
?
?
?
?
?
?
?
?
2
4
31
22
y
x
即
?
?
?
??
???
23
422
yx
yx
,可得
?
?
?
??
??
2
4
y
x
(2)设 ?
?
?
?
?
?
??
dc
ba
A 1 , ?
?
?
?
?
?
??
?
?
?
?
?
?
?
?
?
?
?
10
01
3-1
2-2
dc
ba
, 可 得
?
?
?
?
?
?
?
??
??
??
??
13
03
022
122
db
ca
db
ca
, 解 得
2
1
,
4
1
,
2
1
,
4
3
?????? dcba ,即
?
?
?
?
?
?
?
?
?
?
?
?
??
2
1
4
1
2
1
4
3
1A
B.选修 4—4:坐标系与参数方程
在极坐标系中,已知直线 2)
4
cos(: ??
?
??l 与曲线 ?? sin6: ?C 相交于 BA, 两点,求线段
AB的长.
【解析】 ,2
4
cos ??
?
?
?
?
?
?
?
?? 即 02,2,2sin
2
2
cos
2
2
??????? yxyx????
?? sin6? ,即 ? ? 93,6,sin6 22222 ?????? yxyyx??? ,即圆心 ? ?3,0 , 3?r
点到直线的距离
2
2
2
230
?
??
?d , 34
2
1
92 ???AB
【必做题】第 22 题、第 23 题,每题 10 分,共计 20 分.请在答卷卡指定区域内........作答.解
答应写出文字说明、证明过程或演算步骤.
22. 如图,在正四棱柱
1 1 1 1ABCD A B C D? 中,已知底面 ABCD的边长 3AB ? ,侧棱 1 2AA ? ,
点 E 是棱 1CC 的中点,点 F 满足 .
(1)求异面直线 FE 和 1DB 所成角的余弦值;
(2)记二面角
1E B F A? ? 的大小为? ,求 cos? .
【解析】(1)如图建立空间直角坐标系,则
11
22
||||
,cos
)2,3,3(),1,1,3(
1
1
1
1
?
?
?
???
???
??
??
??
??
DBFE
DBFE
DBFE
DBFE
(2) 设面 FEB1 的法向量 ),,(1 zyxn ?
?
, )2,1,0(1 ???
?
FB .
????
?? FEnFBn 111 ,
)3,6,1(
.3,1,6,
03
02
1 ???
????
?
?
?
????
???
?
n
zxy
zyx
zy
得令
面 FAB1 的法向量为 )0,0,1(2 ?
?
n .
46
46
|
||||
||cos|
21
21 ?
?
?
??
??
??
nn
nn
?
23. (本小题满分 10 分)
本着健康、低碳的生活理念,租用公共自行车骑行的人越来越多,某种公共自行车的租用收
费标准为:每次租车不超过 1 小时免费,超过 1 小时的部分每小时收费 2 元(不足 1 小时的
部分按 1 小时计算).甲、乙令人相互独立来租车,每人各租 1 辆且只租用 1 次。设甲、乙
不超过 1 小时还车的概率分别为
1
4
和
1
2
;1 小时以上且不超过 2 小时还车的概率分别为
1
2
和
1
4
;两人租车时间都不会超过 3 小时。
(1)求甲、乙两人所付租车费用相同的概率;
(2)记甲、乙两人所付的租车费用之和为随机变量 X ,求 X 的分布列和数学期望 ? ?E X .
22、【解析】
(1)
16
5
4
1
4
1
4
1
2
1
2
1
4
1
???????P
(2)
X 0 2 4 6 8
P
8
1
16
5
16
5
16
3
16
1
16
1
4
1
4
1
)8(
16
3
4
1
4
1
4
1
2
1
)6(
16
5
4
1
4
1
2
1
4
1
4
1
2
1
)4(
16
5
4
1
4
1
2
1
2
1
)2(
8
1
2
1
4
1
)0(
????
??????
????????
??????
????
XP
XP
XP
XP
XP
2
7
16
1
8
16
3
6
16
5
4
16
5
2
8
1
0 ???????????EX
数 学 2018 .09
参考公式:
柱体的体积公式:V=Sh,其中 S 为柱体的底面积,h 为柱体的高.
一、填空题:本大题共 14 小题,每小题 5 分,共 70 分.请把答案填写在答题卡相应位置.......
上.
1. 已知集合 ? ?A= |1 5x x x R?< < , , ? ?B= | 2x x n Z? ?,n ,那么集合 A B? 中有______个元
素.
【答案】2
??2,4A B ?∩ ,共有 2 个元素
解析:本题考查了集合中交集的运算.
2. 复数 z (1 )(2 )bi i? ? ? ,其中 b R? , i 为虚数单位 .若 z 是纯虚数,则实数 b 的值为
_________.
【答案】-2
? ?? ? ? ?1 2 2 2 1z bi i b b i? ? ? ? ? ? ? ,
∵ z 是纯虚数,∴ 2 0b? ? ,∴ 2b ? ?
解析:本题考查了复数的计算.
3. 已知某地连续 5 天的最低气温(单位:摄氏度)依次是 18,21,22,24,25,那么这组
数据的方差为_________.
【答案】6
S 2 =
1
5
? 18- 22( )
2
+ 21-22( )
2
+ 22- 22( )
2
+ 24-22( )
2
+ 25-22( )
2é
?ê
ù
?ú
= 6
解析:本题考查了方差的计算.
4. 执行右图所示的算法流程图,则最后输出的 S 的值为_________.
【答案】8
1, 1 3, 2 5, 4 7, 8I S I S I S I S? ? ? ? ? ? ? ? ? ? ?
解析:本题考查了算法的计算
5. 若函数
1
( )
2 1x
f x a? ?
?
是奇函数,则实数 a的值为_________.
【答案】
1
2
∵ ? ?
1
2 1x
f x a? ?
?
是奇函数,
∴ ? ? ? ? 0f x f x? ? ?
1 1
0
2 1 2 1
1 2
2 0
2 1 2 1
1 2
2 0
2 1
2 1 0
1
2
x x
x
x x
x
x
a a
a
a
a
a
?
? ? ? ?
? ?
? ? ?
? ?
?
? ?
?
? ?
?
解析:本题考查了奇函数的相关计算
6. 在平面直角坐标系 xOy 中,若抛物线 2 4y x? 的准线与双曲线
2 2
2 2
1( 0 0
x y
a b
a b
? ? > , > )的
一条渐近线的交点的纵坐标为 2,则该双曲线的离心率是__________.
【答案】 5
抛物线 2 4y x? 的准线是 1x ? ? ,∴双曲线的渐近线过 ? ?1,2? ,
∴渐近线是 2y x? ? ,∴ 2
b
a
? ∴离心率
2
21 1 2 5
c b
e
a a
? ?
? ? ? ? ? ?? ?
? ?
解析:本题考查了抛物线和双曲线的相关性质
7. 不透明的盒子中有大小、形状和质地都相同的 5 只球,其中 2 只白球,3 只红球,现从中
随机取出 2 只球,则取出的这 2 只球颜色相同的概率是________.
【答案】
2
5
解析:考察了简单概率的求解,基础题
8. 已知函数 ( ) 2sin(2 )( )
2 2
f x x
? ?
? ?? ? ? < < 的图像关于直线
6
x
?
? 对称,则 ? ?0f 的值为
________.
【答案】
f (0) = 1
因为关于
x =
p
6
对称,所以
f (x) = ±2,即
sin(
p
3
+j) = ±1,
p
3
+j =
p
2
+ kp (k ?Z),
所以
j =
p
6
+ kp (k ?Z),因为
j ?(-
p
2
,
p
2
),所以
j =
p
6
.
f (0) = 1
解析:考察了正弦函数的对称轴问题,基础题
9. 如图,在三棱柱
1 1 1ABC A B C? 中, =2AB , 1=3AA ,则四棱锥 1 1 1-A B C CB的体积是_______.
【答案】 2 3
四棱锥高为 h = 3,
V =
1
3
? 2 ? 3? 3 = 2 3.
解析:考察了空间集合体的体积,基础题
10. 在数列? ?na 中,已知 1 1a ? , 1
1
( 1)
n na a
n n
? ? ?
?
*( )n N? ,则 10a 的值为____________.
【答案】
19
10
? ? ? ? ? ?10 10 9 9 8 2 1 1a a a a a a a a? ? ? ? ? ? ? ?L L
1 1 1 1 1 1 19
1 1 1 1
9 10 8 9 2 10 10
? ? ? ? ? ? ? ? ? ? ? ?L L
解析:中档题,考察数列累加法
11. 已知 ABC? 的面积为3 15 ,且 2AC AB? ? ,
1
cos
4
A ? ? ,则 BC 的长为___________.
【答案】8
∵
1
cos
4
A ? ? , ? ?0,A ??
∴
15
sin
4
A ?
∵
1
sin 3 15
2
ABCS bc A? ? ?
∴ 24bc ?
又 2b c? ?
∴ ? ?
22 2 2 25 52 cos 2 24 64
2 2
a b c bc A b c bc? ? ? ? ? ? ? ? ? ?
∴ 8BC ?
解析:中档题,考察解三角形的相关知识
12. 在菱形 ABCD中, 60ABC ?? ? ,E 为边 BC 上一点,且 , ,则
的值为_________.
【答案】
9
2
?
设 ,
则
∴ 2 9a ?
∴
解析:中档题,考察向量的基本运算
13. 在平面直角坐标系 xOy 中,已知点 (1,1)A , (1, 1)B ? ,点 P 为圆 2 2( 4) 4x y? ? ? 上任意一
点,记 OAP? 和 OBP? 的面积分别为
1S 和 2S ,则
1
2
S
S
的最小值是_________.
【答案】 32 ?
解析:设点 ? ??? sin2,cos24?P , xylxyl OBOA ??? :,:
2
sin2cos24
2
2
1
1
???
???S 同理
2
sin2cos24
2
2
1
2
?? ??
???S
则 ?
??
??
?
??
??
sin2cos24
sin2cos24
2
1
S
S
4 2 2 sin 2 sin
4 4
4 2 2 cos 2 cos
4 4
? ?
? ?
? ?
? ?
? ? ? ?
? ? ? ?? ? ? ?
? ? ? ?
?
? ? ? ?
? ? ? ?? ? ? ?
? ? ? ?
设点 ? ?2,2 ??M ,点 cos ,sin
4 4
N
? ?
? ?
? ?? ? ? ?
? ?? ?? ? ? ?
? ? ? ?? ?
可知点 N 落在单位圆上
问题可转化为点M 和点 N 构成直线斜率绝对值的最小值
设直线 ? ?22 ??? xky 与单位圆相切
得 32??k 得最小值为 32 ?
14. 若函数 2
1
( ) 1
2
xf x ax e? ? ? 在 1x x? 和 2x x? 两处取到极值,且
2
1
2
x
x
? ,则实数 a 的取值
范围是___________.
【答案】 ?
?
?
?
?
?
??,
2ln
2
解析:函数 ? ?f x 求导得 ? ?' xf x ax e? ?
由题知有① 1
1
x
ax e? ,② 22
x
ax e? ,
②
①
: 2 12
1
x xx
e
x
?
? ,
令 ? ?2
1
2
x
t t
x
? ? ,则有 1 1tx xe t? ? ,得
1
ln
1
t
x
t
?
?
令 ? ?
ln
1
t
f t
t
?
?
, ? ?
? ?
'
2
1
1 ln
1
t
tf t
t
? ?
?
?
,
再令 ? ?
1
1 lng t t
t
? ? ? , ? ?'
2
1 t
g t
t
?
? ,又因 2t ? ,则 ? ?g t 在 ? ?2,?? 为减函数,
? ?
max
1
ln 2 0
2
g t ? ? < ,则 ? ?' 0f t < , ? ? ? ?
max
2 ln 2f t f? ?
则有
1 ln 2x ? 。由①得
1
1
x
e
a
x
? ,令 ? ? ? ?
? ?11 1'
1 1 2
1 1
1
,F
xx e xe
F x x
x x
?
? ? ,
则 ? ?1F x 在 ? ?0,1 2n 为减函数, ? ? ? ?1 min
2
ln 2
ln 2
F x F? ? ,
则
2
ln 2
a ? , a的取值范围是
2
,
ln 2
? ?
????
? ?
。
二、解答题:本大题共 6 小题,共计 90 分.请在答题卡指定区域内........作答,解答时应写出文
字说明、证明过程或演算步骤.
15.(本小题满分 14 分)
如图,已知四边形 ABCD是矩形,平面 ABCD ?平面BCE , ECBC ? , F 是BE 的中点。
(1)求证:DE //平面 ACF ;
(2)求证:平面 AFC ?平面 ABE .
【解析 】 (1)连接 BD交 AC 于点G ,连接 FG
F 、G 分别为 BE 、 BD的中点
/ /FG DE?
平面 ACF
DE ?平面 ACF
/ /DE? 平面 ACF .
(2) , F 为 BE 中点,
CF BE? ?
平面 ABCD ?平面 BCE
平面 ABCD ∩平面 BCE = BC
又 平面 ABCD, AB BC?
AB? ?平面 BCE
平面 BCE
AB CF? ?
平面 ABE, BE ?平面 ABE,
AB∩BE = B
CF? ?平面 ABE
平面 AFC
?平面 AFC ?平面 ABE .
16.(本小题满分 14 分)
已知 ??, 为钝角,且
5
3
sin ?? ,
5
3
2cos ??? .
(1)求 ?tan 的值;
(2)求 ? ??? ?2cos 的值.
【解析】
(1)
5
3
sincos
sincos
sincos2cos
22
22
22 ??
?
?
???
??
??
???
4tan2 ?? ? 2tan ??? ?
(2)
? ? ?????? sin2sincos2cos2cos ???
25
7
2cos ??
, 25
24
2sin ???
5
5
cos,
5
52
sin ??? ??
? ??? ??2cos 125
541
17.(本小题满分 14 分)
销售甲种商品所得利润是P 万元,它与投入资金 t 万元的关系有经验公式
1?
?
t
at
P ;销售乙
种商品所得利润是Q万元,它与投入资金 t 万元的关系有经验公式 btQ ? ,其中 ba, 为常数.
现将 3 万元全部投入甲、乙两种商品的销售:若全部投入甲种商品,所得利润为
4
9
万元;
若全部投入乙种商品,所得利润为 1 万元.若将 3 万元资金中的 x 万元投入甲种商品的销售,
余下的投入乙种商品的销售,则所得利润总和为 )(xf 万元.
(1)求函数 )(xf 的解析式;
(2)怎样将 3 万元资金分配给甲、乙两种商品,才能使所得利润总和最大,并求出最大值.
【解析】(1)由已知
??
?
?
?
?
?
?
??
?
?
?
?
?
3
1
3
13
4
9
4
3
b
a
b
a
]3,0[),
1
9
(
3
1
4)3(
3
1
1
3
)( ?
?
?????
?
?? x
x
xx
x
x
xf
(2) 51
1
9
1
1
9
??
?
???
?
?
x
x
x
x? ,当且仅当 ""2
1
1
1 ??
?
?? 时取,即x
x
x
3
7
3
5
4)( ???? xf
答:投资甲 2 万元,乙 1 万元时,利润总和最大,为
3
7
万元
18.(本小题满分 16 分)
在平面直角坐标系 xOy中,椭圆 E :
x2
a2
+
y2
b2
= 1 a > b > 0( )的离心率为 2
2
,且直线 l : x = 2
被椭圆 E截得的弦长为 2,与坐标轴不垂直的直线交椭圆 E于 P,Q两点,且 PQ的中点 R在
直线 l上.点 M 1,0( ).
(1)求椭圆 E的方程;
(2)求证: MR ^ PQ
【解析】(1)椭圆过点 ? ?2,1
2
2
2 2
2
62
4 1 3
1
c
e
aa
b
a b
?
? ?? ? ?? ?
?? ?
??? ?? ?
??
椭圆方程为
2 2
1
6 3
x y
? ?
(2)Q直线 l 于坐标轴不垂直
?斜率存在
设 ? ? ? ?1 1 2 2, , ,P x y Q x y
? ?? ? ? ?? ?
2 2
1 1
1 2 1 2 1 2 1 2
2 2
2 2
1
6 3
0
6 3
1
6 3
x y
x x x x y y y y
x y
?
? ?? ? ? ? ??
? ? ??
? ? ?
??
? ?
1 2 1 2
1 2 1 22
y y x x
x x y y
? ?
? ? ?
? ?
为 PQ重点,且落在直线上
1 2
1 2
4
2
PQ
x x
k
y y
? ? ?
? ? ?
?
1 2
2
MR
y y
k
?
? ?
1PQ MRk k MR PQ? ? ? ? ? ?
19.(本小题满分 16 分)
已知函数 f x( ) = ln x,g x( ) = x2
(1) 求过原点 0,0( ),且与函数 f x( )的图像相切的直线 l的方程;
(2) 若 a > 0,求函数j x( ) = g x( )- 2a2 f x( ) 在区间 1,+?é? )上的最小值.
【解析】(1)设切点坐标 ? ?0 0, lnx x , ? ?
1
f x
x
? ? ,
设切线方程: ? ?0 0
0
1
lny x x x
x
? ? ? ,代入 ? ?0,0 ,得 0x e?
即切线方程为
1
y x
e
?
(2)设 ? ? ? ? ? ?22h x g x a f x? ? = 2 22 lnx a x?
? ?
? ?? ?2 22
2 =
x a x aa
h x x
x x
? ?
? ? ?
令 ? ?=0h x? 得, x a? (负值舍)
当 0 1a? ? 时, ? ? 0h x? ? 在 ? ?1,?? 上恒成立,所以函数 ? ?h x 单调递增,
? ? ? ?min 1 1 0h x h? ? ?
所以 ? ?min 1x? ?
当 1a ? 时,可得 ? ?h x 在 ? ?1,a 上单调递减,在 ? ?,a ?? 上单调递增,
故 ? ? ? ? ? ?2 2 2min 2 ln 1 2lnh x h a a a a a a? ? ? ? ?
1 o当1 2ln 0a? ? ,即 a e? 时, ? ? ? ?2min 1 2lnx a a? ? ?
2 o当1 2ln 0a? ? ,即 a e? 时,又 ? ?1 1 0? ? ? ,所以 ? ?min 0x? ?
综上所述,
当 0 1a? ? 时, ? ?min 1x? ? ;
当1 a e? ? 时, ? ? ? ?2min 1 2lnx a a? ? ? ;
当 a e? 时, ? ?min 0x? ? .
20.(本小题满分 16 分)
如果数列 an{ }共有 k k ?N
*,k ? 4( )项,且满足条件:
则称数列 an{ }为 P k( )数列.
(1)若等比数列 an{ }为 P 4( )数列,求 a1的值;
(2)已知 m为给定的正整数,且m ? 2
①若公差为正数的等差数列 an{ }是 P 2m+ 3( )数列,求数列 an{ }的公差
②若 a
n
=
qn-1
3
,1? n ? m,n ?N *
m - n
12
,m+1? n ? 2m,n?N *
ì
í
??
?
?
?
,其中 q为常数, q < -1判断数列 an{ }是否为
P 2m( )数列,说明理由.
【解析】(1)当公比为 1 时明显不符合
当公比不为 1 时,
a
1
+ a
2
+ a
3
+ a
4
=
a
1
(1- q4 )
1- q
= 0,得到
q = -1
a
1
+ a
2
+ a
3
+ a
4
= 4 a
1
=1
所以
a
1
= ±
1
4
(2)①
a
n{ }为等差数列
a
1
+ a
2
+×××+ a
2m+3
= (2m+3)a
m+2
= 0
所以
a
m+2
= 0
因为 d > 0
则
a
1
+ a
2
+×××+ a
2m+3
= -a
1
- a
2
- a
m+1
+0+ a
m+3
+×××+ a
2m+3
= (m+2)(m+1)d =1
化简得
d =
1
(m+ 2)(m+1)
②令 2 1 2 2
1 ( 1)
0
3(1 ) 24
m
m m
q m m
S a a a
q
? ?
? ? ? ?? ? ? ? ? ?
?
得
1- qm =
(1- q)m(m+1)
8
令 2 1 2 2
1 ( ) ( 1)
1
3(1 ) 24
m
m m
q m m
T a a a
q
? ? ?
? ? ? ?? ? ? ? ? ?
?
得
1- (-q)m =
(24- m(m+1))(1+ q)
8
当 m为偶数时
(1-q)m(m+1)
8
=
(24- m(m+1))(1+q)
8
化简得
m2 + m =12(1+q)
因为
q < -1,m ? 2,所以不存在 m,
q使得等式成立
当 m为奇数时
2 =
(1- q)m(m+1)
8
+
(24- m(m+1))(1+q)
8
化简得
m2 + m-12 =
4
q
因为
q < -1,m ? 2
m
2 + m-12 < 0, -4 < m< 3
所以不存在 m,
q使得等式成立
综上,
a
n{ }不可能是 P(2m)数列
南京市 2019 届高三年级学情调研卷
数学附加题 2018.09
注意事项:
1.附加题供选修物理的考生使用.
2.本试卷共 40 分,考试时间 30 分钟.
3.答题前,考生务必将自己的姓名、学校写在答题卡上.试题的答案写在答题卡...上对
应题目的答案空格内.考试结束后,交回答题卡.
21.【选做题】在 A、B、C、D 四小题中只能选做 2 题,每小题 10 分,共计 20 分.请在答.
卷卡指定区域内.......作答.解答应写出文字说明、证明过程或演算步骤.
A.选修 4—2:矩阵与变换
已知矩阵
31
22
?
?
?A ,向量 ?
?
?
?
?
??
?
2
4
? .
(1)若向量 ?
?
?
?
?
?
?
y
x
? 满足 ?? ?A ,求 yx, 的值;
(2)求 1?A .
(1) ?
?
?
?
?
??
??
?
?
?
?
?
?
?
?
?
?
?
?
?
2
4
31
22
y
x
即
?
?
?
??
???
23
422
yx
yx
,可得
?
?
?
??
??
2
4
y
x
(2)设 ?
?
?
?
?
?
??
dc
ba
A 1 , ?
?
?
?
?
?
??
?
?
?
?
?
?
?
?
?
?
?
10
01
3-1
2-2
dc
ba
, 可 得
?
?
?
?
?
?
?
??
??
??
??
13
03
022
122
db
ca
db
ca
, 解 得
2
1
,
4
1
,
2
1
,
4
3
?????? dcba ,即
?
?
?
?
?
?
?
?
?
?
?
?
??
2
1
4
1
2
1
4
3
1A
B.选修 4—4:坐标系与参数方程
在极坐标系中,已知直线 2)
4
cos(: ??
?
??l 与曲线 ?? sin6: ?C 相交于 BA, 两点,求线段
AB的长.
【解析】 ,2
4
cos ??
?
?
?
?
?
?
?
?? 即 02,2,2sin
2
2
cos
2
2
??????? yxyx????
?? sin6? ,即 ? ? 93,6,sin6 22222 ?????? yxyyx??? ,即圆心 ? ?3,0 , 3?r
点到直线的距离
2
2
2
230
?
??
?d , 34
2
1
92 ???AB
【必做题】第 22 题、第 23 题,每题 10 分,共计 20 分.请在答卷卡指定区域内........作答.解
答应写出文字说明、证明过程或演算步骤.
22. 如图,在正四棱柱
1 1 1 1ABCD A B C D? 中,已知底面 ABCD的边长 3AB ? ,侧棱 1 2AA ? ,
点 E 是棱 1CC 的中点,点 F 满足 .
(1)求异面直线 FE 和 1DB 所成角的余弦值;
(2)记二面角
1E B F A? ? 的大小为? ,求 cos? .
【解析】(1)如图建立空间直角坐标系,则
11
22
||||
,cos
)2,3,3(),1,1,3(
1
1
1
1
?
?
?
???
???
??
??
??
??
DBFE
DBFE
DBFE
DBFE
(2) 设面 FEB1 的法向量 ),,(1 zyxn ?
?
, )2,1,0(1 ???
?
FB .
????
?? FEnFBn 111 ,
)3,6,1(
.3,1,6,
03
02
1 ???
????
?
?
?
????
???
?
n
zxy
zyx
zy
得令
面 FAB1 的法向量为 )0,0,1(2 ?
?
n .
46
46
|
||||
||cos|
21
21 ?
?
?
??
??
??
nn
nn
?
23. (本小题满分 10 分)
本着健康、低碳的生活理念,租用公共自行车骑行的人越来越多,某种公共自行车的租用收
费标准为:每次租车不超过 1 小时免费,超过 1 小时的部分每小时收费 2 元(不足 1 小时的
部分按 1 小时计算).甲、乙令人相互独立来租车,每人各租 1 辆且只租用 1 次。设甲、乙
不超过 1 小时还车的概率分别为
1
4
和
1
2
;1 小时以上且不超过 2 小时还车的概率分别为
1
2
和
1
4
;两人租车时间都不会超过 3 小时。
(1)求甲、乙两人所付租车费用相同的概率;
(2)记甲、乙两人所付的租车费用之和为随机变量 X ,求 X 的分布列和数学期望 ? ?E X .
22、【解析】
(1)
16
5
4
1
4
1
4
1
2
1
2
1
4
1
???????P
(2)
X 0 2 4 6 8
P
8
1
16
5
16
5
16
3
16
1
16
1
4
1
4
1
)8(
16
3
4
1
4
1
4
1
2
1
)6(
16
5
4
1
4
1
2
1
4
1
4
1
2
1
)4(
16
5
4
1
4
1
2
1
2
1
)2(
8
1
2
1
4
1
)0(
????
??????
????????
??????
????
XP
XP
XP
XP
XP
2
7
16
1
8
16
3
6
16
5
4
16
5
2
8
1
0 ???????????EX
同课章节目录
