23.1 图形的旋转同步课时作业(2)
图片预览

文档简介
23.1 图形的旋转同步课时作业(2)
姓名:___________班级:___________考号:___________
一、选择题
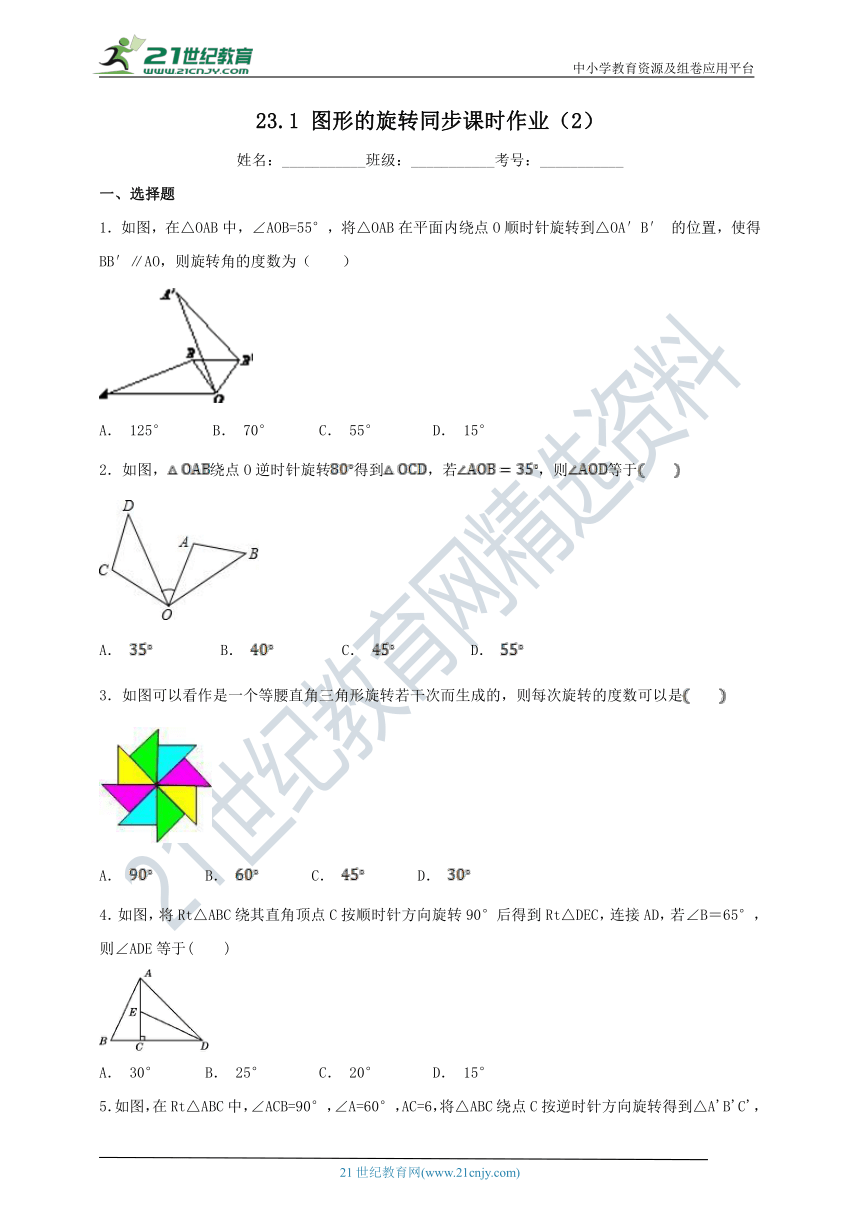
1.如图,在△OAB中,∠AOB=55°,将△OAB在平面内绕点O顺时针旋转到△OA′B′ 的位置,使得BB′∥AO,则旋转角的度数为( )
A. 125° B. 70° C. 55° D. 15°
2.如图,绕点O逆时针旋转得到,若,则等于
A. B. C. D.
3.如图可以看作是一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数可以是
A. B. C. D.
4.如图,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠B=65°,则∠ADE等于( )
A. 30° B. 25° C. 20° D. 15°
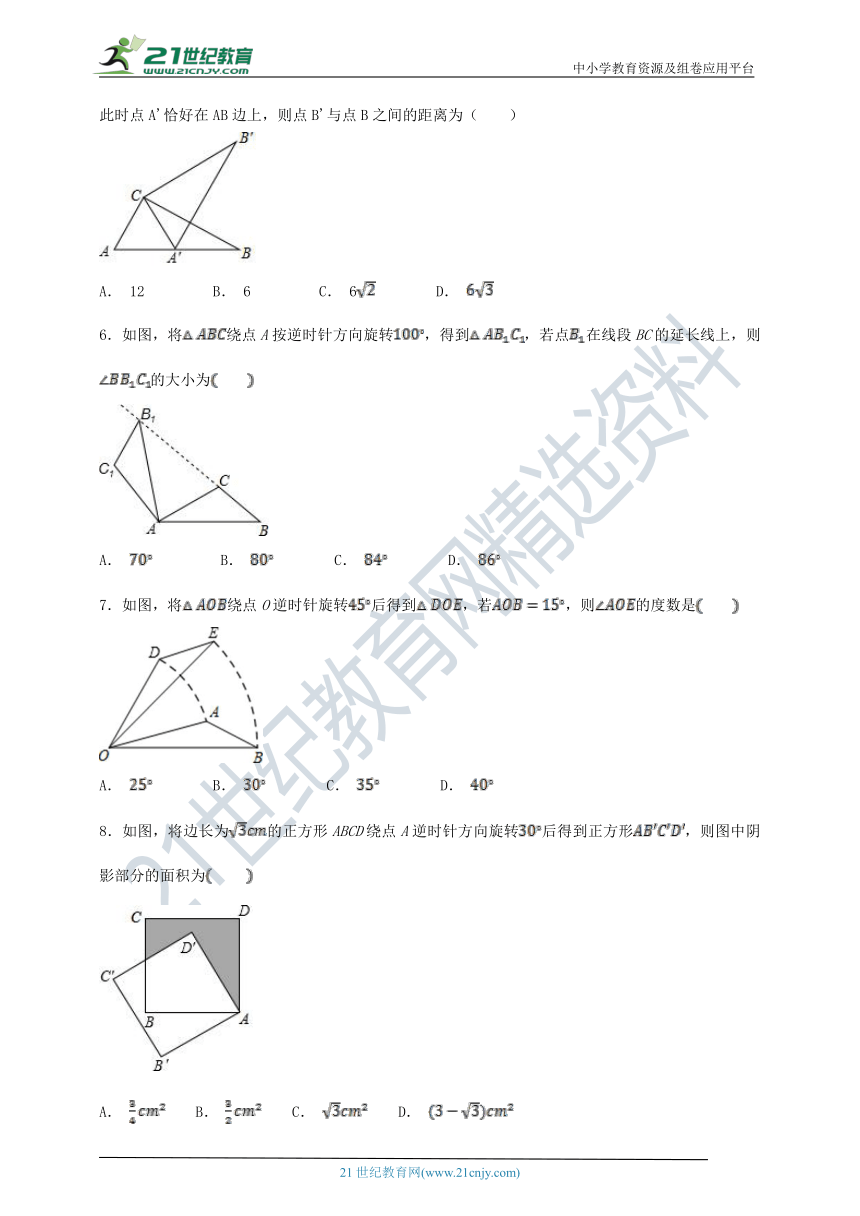
5.如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
A. 12 B. 6 C. 6 D.
6.如图,将绕点A按逆时针方向旋转,得到,若点在线段BC的延长线上,则的大小为
A. B. C. D.
7.如图,将绕点O逆时针旋转后得到,若,则的度数是
A. B. C. D.
8.如图,将边长为的正方形ABCD绕点A逆时针方向旋转后得到正方形,则图中阴影部分的面积为
A. B. C. D.
二、填空题
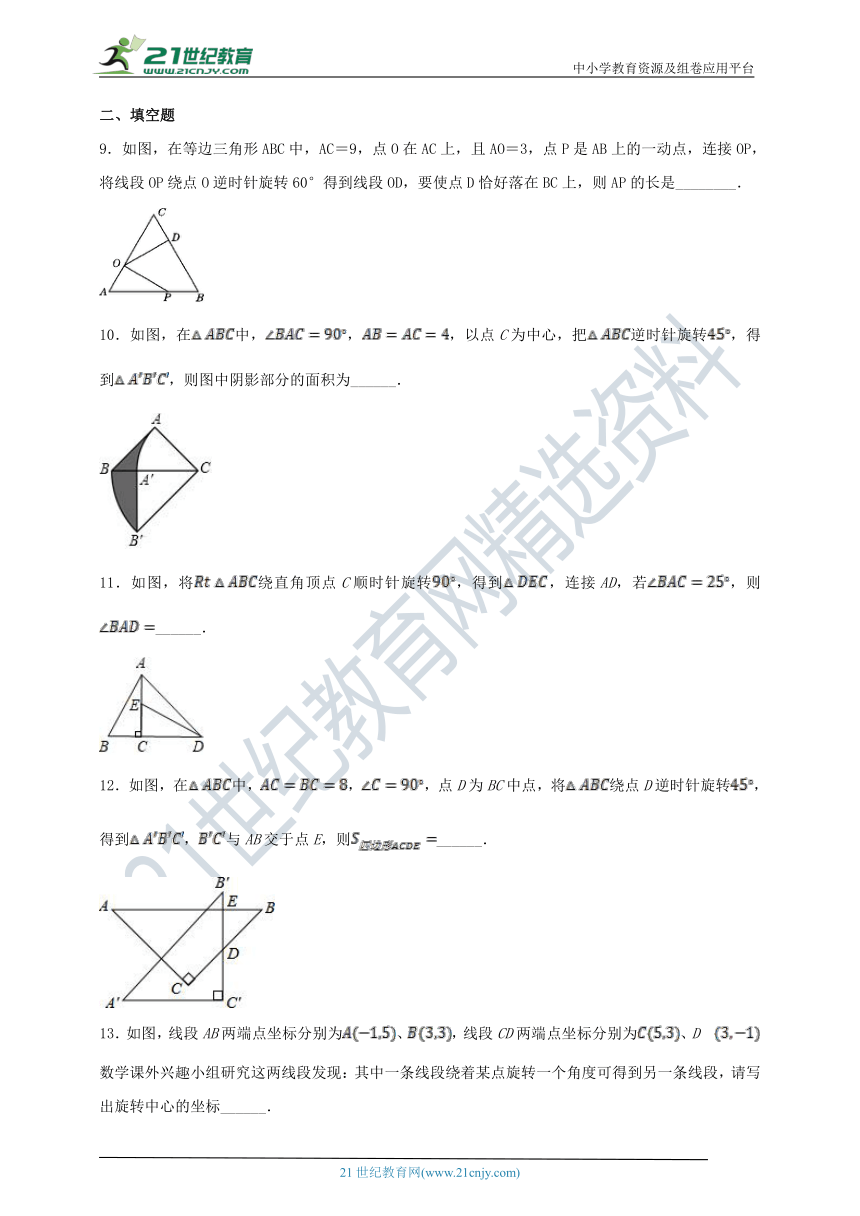
9.如图,在等边三角形ABC中,AC=9,点O在AC上,且AO=3,点P是AB上的一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是________.
10.如图,在中,,,以点C为中心,把逆时针旋转,得到,则图中阴影部分的面积为______.
11.如图,将绕直角顶点C顺时针旋转,得到,连接AD,若,则______.
12.如图,在中,,,点D为BC中点,将绕点D逆时针旋转,得到,与AB交于点E,则______.
13.如图,线段AB两端点坐标分别为、,线段CD两端点坐标分别为、D?数学课外兴趣小组研究这两线段发现:其中一条线段绕着某点旋转一个角度可得到另一条线段,请写出旋转中心的坐标______.
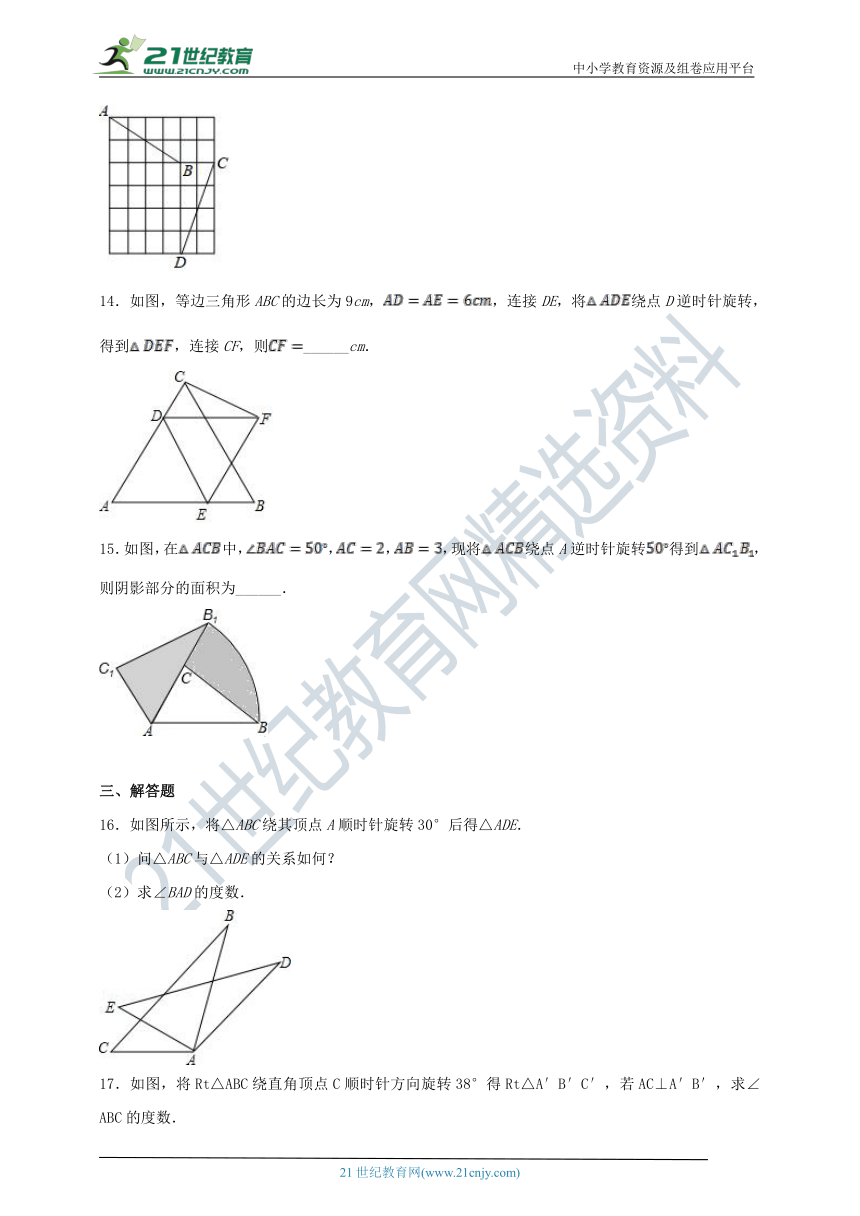
14.如图,等边三角形ABC的边长为9cm,,连接DE,将绕点D逆时针旋转,得到,连接CF,则______cm.
15.如图,在中,,,,现将绕点A逆时针旋转得到,则阴影部分的面积为______.
三、解答题
16.如图所示,将△ABC绕其顶点A顺时针旋转30°后得△ADE.
(1)问△ABC与△ADE的关系如何?
(2)求∠BAD的度数.
17.如图,将Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,若AC⊥A′B′,求∠ABC的度数.
18.如图,△ABC由△EDC绕C点旋转得到,B、C、E三点在同一条直线上,∠ACD=∠B,求证:△ABC是等腰三角形.
19.如图,在正方形ABCD中,E为DC边上的点,连接BE,将绕点C顺时针方向旋转得到,连结EF,若,求的度数.
20.如图,点A′在Rt△ABC的边AB上,与BC交于点D,∠ABC=30°,AC=2,∠ACB=90°,△ACB绕顶点C按逆时针方向旋转与△A′CB′重合,连接BB′,求线段BB′的长度.
21.已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
22.已知:在平面直角坐标系中,点A、B分别在x轴正半轴上,且线段OA、OB(OA<OB)的长分别等于方程的两个根,点C在轴正半轴上,且OB=2OC.
(1)求A、B、C三点坐标;
(2)将△OBC绕点C顺时针旋转90°后得到,求直线的表达式.
参考答案
1.B
【解析】
【分析】
据两直线平行,内错角相等可得,根据旋转的性质可得,然后利用等腰三角形两底角相等可得,即可得到旋转角的度数.
【详解】
,
,
又 ,
中,,
旋转角的度数为.
故选:.
【点睛】
本题考查了旋转的性质,等腰三角形两底角相等的性质,熟记性质并准确识图是解题的关键.
2.C
【解析】
【分析】
根据旋转的性质可知,D和B为对应点,∠DOB为旋转角,即∠DOB=80°,
所以∠AOD=∠DOB﹣∠AOB.
【详解】
根据旋转的性质可知,D和B为对应点,∠DOB为旋转角,即∠DOB=80°,
所以∠AOD=∠DOB﹣∠AOB=80°﹣35°=45°.
故选:C
【点睛】
本题考核知识点:旋转性质. 解题关键点:理解旋转的性质.
3.C
【解析】
【分析】
根据旋转的性质,观察图形,中心角是由8个度数相等的角组成,结合周角是360°,求得每次旋转的度数.
【详解】
中心角是由8个度数相等的角组成,
每次旋转的度数可以为,
故选C.
【点睛】
本题考查了旋转的性质,运用数形结合思想、发现8个相等的中心角构成一个周角是解题的关键.
4.C
【解析】
【详解】
由题意得,∠B=∠CED=65°,AC=DC,
∴∠CAD=∠CDA=45°,
∴∠ADE=∠CED-∠CAD=65-45=20.
故选C.
5.D
【解析】
【分析】
连接B'B,利用旋转的性质和直角三角形的性质解答即可.
【详解】
连接B'B,
∵将△ABC绕点C按逆时针方向旋转得到△A'B'C,
∴AC=A'C,AB=A'B,∠A=∠CA'B'=60°,
∴△AA'C是等边三角形,
∴∠AA'C=60°,
∴∠B'A'B=180°-60°-60°=60°,
∵将△ABC绕点C按逆时针方向旋转得到△A'B'C,
∴∠ACA'=∠BAB'=60°,BC=B'C,∠CB'A'=∠CBA=90°-60°=30°,
∴△BCB'是等边三角形,
∴∠CB'B=60°,
∵∠CB'A'=30°,
∴∠A'B'B=30°,
∴∠B'BA'=180°-60°-30°=90°,
∵∠ACB=90°,∠A=60°,AC=6,
∴AB=12,
∴A'B=AB-AA'=AB-AC=6,
∴B'B=6,
故选D.
【点睛】
此题考查旋转问题,关键是利用旋转的性质和直角三角形的性质解答.
6.B
【解析】
【分析】
由旋转的性质可知,,由等腰三角形的性质和三角形的内角和定理可求得,从而可求得.
【详解】
解:由旋转的性质可知:,,.
,,
.
.
.
故选:B.
【点睛】
本题主要考查的是旋转的性质,由旋转的性质得到为等腰三角形是解题的关键.
7.B
【解析】
【分析】
由已知求出旋转角,再根据角的和差关系求得∠AOE=∠BOE-∠AOB=45?-15?.
【详解】
由已知可得,旋转角:∠BOE=45?,所以,∠AOE=∠BOE-∠AOB=45?-15?=30?.
故选:B
【点睛】
本题考核知识点:旋转角,角的和差倍. 解题关键点:理解旋转角的定义.
8.D
【解析】
【分析】
设BC、C'D'相交于点M,连结AM,根据HL即可证明△AD'M≌△ABM,可得到∠MAB=30°,然后可求得MB的长,从而可求得△ABM的面积,最后利用正方形的面积减去△AD'M和△ABM的面积进行计算即可.
【详解】
设BC、相交于点M,连结AM,
由旋转的性质可知:,
在Rt和Rt△ABM中
,
≌(HL),
,,
,
,
又,
,
,
又,
,
故选D.
【点睛】
本题考查旋转的性质以及全等三角形的判定与性质、特殊锐角三角函数值的应用,熟练掌握相关性质与定理、证得≌是解本题的关键.
9.6
【解析】
【详解】
由题意得,∵∠A+∠APO=∠POD+∠COD,∠A=∠POD=60°,
∴∠APO=∠COD,
在△AOP与△CDO中,
,
∴△AOP≌△CDO(AAS),
∴AP=CO=AC﹣AO=9﹣3=6.
故答案为6.
10.
【解析】
【分析】
先在中利用勾股定理求出,再根据旋转的性质得出≌,然后根据阴影部分的面积扇形的面积的面积的面积扇形的面积,代入数值解答即可.
【详解】
在中,,,
,
把逆时针旋转,得到,
,,,,
阴影部分的面积,
故答案为.
【点睛】
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等也考查了勾股定理以及扇形面积公式的应用.
11.
【解析】
【分析】
根据旋转的性质可得AC=CD,再判断出△ACD是等腰直角三角形,然后根据等腰直角三角形的性质求出∠CAD=45°,由∠BAD=∠BAC+∠CAD可得答案.
【详解】
∵Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,
∴AC=CD,
∴△ACD是等腰直角三角形,
∴∠CAD=45°,
则∠BAD=∠BAC+∠CAD=25°+45°=70°,
故答案为:70°°.
【点睛】
本题考查了旋转的性质、等腰直角三角形的判定与性质,熟练掌握相关性质并准确识图是解题的关键.
12.28
【解析】
【分析】
利用旋转的性质得出,,进而由求出即可.
【详解】
由题意可得:,,
则,
,
,
,
.
故答案为:28.
【点睛】
考查了旋转的性质以及三角形面积求法,得出是解题关键.
13.或
【解析】
【分析】
分点A的对应点为C或D两种情况考虑:当点A的对应点为点C时,连接AC、BD,分别作线段AC、BD的垂直平分线交于点E,点E即为旋转中心;当点A的对应点为点D时,连接AD、BC,分别作线段AD、BC的垂直平分线交于点M,点M即为旋转中心此题得解.
【详解】
当点A的对应点为点C时,连接AC、BD,分别作线段AC、BD的垂直平分线交于点E,如图1所示:
点的坐标为,B点的坐标为,
点的坐标为;
当点A的对应点为点D时,连接AD、BC,分别作线段AD、BC的垂直平分线交于点M,如图2所示:
点的坐标为,B点的坐标为,
点的坐标为.
综上所述:这个旋转中心的坐标为或.
故答案为:或.
【点睛】
本题考查了坐标与图形变化中的旋转,根据给定点的坐标找出旋转中心的坐标是解题的关键.
14.
【解析】
【分析】
由等边三角形ABC的边长为9cm,可得,,将绕点D逆时针旋转,得到,可得可证为等边三角形,可得,则可得,可得为直角三角形,再根据勾股定理可求CF的长.
【详解】
如图:
是等边三角形
,且,
,是等边三角形.
将绕点D逆时针旋转,得到
,且
,且
为等边三角形
,
,
,
为直角三角形,且,,
,
故答案为
【点睛】
本题考查等边三角形的性质,旋转的性质,直角三角形的判定,勾股定理,本题关键是证明为直角三角形.
15.
【解析】
【分析】
根据旋转的性质可知S△ABC=S△AB1C1,由此可得S阴影=S扇形ABB1,根据扇形面积公式即可得出结论.
【详解】
∵S△ABC=S△AB1C1,
∴S阴影=S扇形ABB1=πAB2=π.
故答案为:π.
【点睛】
本题考查了旋转的性质以及扇形的面积公式,解题的关键是找出S阴影=S扇形ABB1.本题属于基础题,难度不大,解决该题型题目时,根据旋转的性质找出阴影部分的面积等于扇形的面积是关键.
16.(1)△ABC≌△ADE;(2)30°
【解析】由旋转的性质和三角形的性质即可解答.
解:(1)∵△ABC绕其顶点A顺时针旋转30°后得△ADE,∴△ABC≌△ADE.
(2)旋转角相等,即∠BAD=∠EAC=30°.
17.38°.
【解析】分析:
如下图所示,设AC与A′B′的交点为O,则由已知条件易得∠A′OC=90°,∠ACA′=38°,由此可得∠A′=52°,由旋转的性质可得∠A=52°,结合∠ACB=90°即可得到∠ABC=38°.
详解:
∵Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,
∴∠ACA′=38°,∠A=∠A′,
∵AC⊥A′B′,
∴∠A′OC=90°,
∴∠A′=90°-38°=52°,
∴∠A=52°,
又∵在Rt△ABC中,∠ACB=90°,
∴∠ABC=180°-90°-52°=38°.
点睛:“由旋转的性质得到∠ACA′=38°,结合AC⊥A′B′得到∠A′=52°=∠A”是解答本题的关键.
18.见解析
【解析】
【分析】
由旋转的性质可知∠D=∠B,再根据已知条件证明AC∥DE,进而证明∠ACB=∠A,所以△ABC是等腰三角形.
【详解】
证明:由旋转知∠D=∠B,
∵∠ACD=∠B,
∴∠ACD=∠D,AC∥DE,
∴∠ACB=∠E,
又∵∠A=∠E,
∴∠ACB=∠A,
∴△ABC是等腰三角形.
【点睛】
本题考查了旋转的性质以及等腰三角形的判定,对于旋转的性质用到最多的是:旋转前、后的图形全等.
19.15°
【解析】
【分析】
根据旋转性质可得:,,,由等腰直角三角形三角形性质可得,所以.
【详解】
解:是旋转得到的图形, ,,, . .
【点睛】
本题考核知识点:旋转性质,等腰直角三角形. 解题关键点:熟记旋转性质,等腰直角三角形性质.
20.BB′=BC=2.
【解析】
【分析】
Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,可得AB=2AC=4,由勾股定理得BC==2;再证△AA′C是等边三角形,得AA′=AB=2,A′C=A′B,可得∠A′CB=∠A′BC=30°,
由旋转得∠A′CB′=90°,BC=B′C,所以∠B′CB=90°﹣30°=60°,证得△BCB′是等边三角形,所以BB′=BC=2.
【详解】
解:∵Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,
∴BC==2,
∵∠A=60°,
∴△AA′C是等边三角形,
∴AA′=AB=2,
∴A′C=A′B,
∴∠A′CB=∠A′BC=30°,
∵△A′B′C是△ABC旋转而成,
∴∠A′CB′=90°,BC=B′C,
∴∠B′CB=90°﹣30°=60°,
∴△BCB′是等边三角形,
∴BB′=BC=2.
【点睛】
本题考核知识点:旋转,直角三角形,等边三角形的判定和性质. 解题关键点:熟记旋转性质和等边三角形的判定和性质.
21.(1)证明见解析;(2)5.
【解析】
【分析】
(1)直接利用旋转的性质可得AP=AQ,∠PAQ=60°,然后根据“SAS”证明△BAP≌△CAQ,结合全等三角形的性质得出答案;
(2)由△APQ是等边三角形可得AP=PQ=3,∠AQP=60°,由全等的性质可得∠AQC =∠APB=150°,从而可求∠PQC=90°,然后根据勾股定理求PC的长即可.
直接利用等边三角形的性质结合勾股定理即可得出答案.
【详解】
(1)证明:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中
,
∴△BAP≌△CAQ(SAS),
∴PB=QC;
(2)解:∵由(1)得△APQ是等边三角形,
∴AP=PQ=3,∠AQP=60°,
∵∠APB=150°,
∴∠PQC=150°﹣60°=90°,
∵PB=QC,
∴QC=4,
∴△PQC是直角三角形,
∴PC===5.
【点睛】
本题考查了旋转的性质,等边三角形的性质与判定,全等三角形的判定与性质,勾股定理.证明△BAP≌△CAQ是解(1)的关键,证明∠PQC=90°是解(2)的关键.
22.(1) A(1,0)、B(4,0)、 C(0,2); (2)
【解析】
【分析】
(1)先利用因式分解法解方程x2-5x+4=0可确定A(1,0)、B(4,0);再利用OB=2OC,且点C在y轴正半轴上可确定C点坐标;
(2)利用旋转的性质得OB=O′B′=4,OC=O′C′=2,∠COB=∠C0′B′=90°,∠OCO′=∠BCB′=90°,则可确定O′(-2,2)、B′(-2,-2),然后利用待定系数法求直线B′C的解析式.
【详解】
(1) ∵OA、OB的长是方程2-5+4=0的两个根,且OA<OB,
解得
∴OA=1,OB=4
∵A、B分别在x轴正半轴上,
∴A(1,0)、B(4,0)
又∵OB2OC,且点C在轴正半轴上
∴OC2,C(0,2)
(2) ∵ 将△OBC绕点C顺时针旋转90°后得到
∴OB=O′B′=4,OC=O′C′=2,∠COB=∠C0′B′=90°,∠OCO′=∠BCB′=90°
∴O′(-2,2)、B′(-2,-2)
设直线B′C的解析式为
∴,解得
∴直线B′C的解析式为.
【点睛】本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了旋转的性质和待定系数法求一次函数解析式.
姓名:___________班级:___________考号:___________
一、选择题
1.如图,在△OAB中,∠AOB=55°,将△OAB在平面内绕点O顺时针旋转到△OA′B′ 的位置,使得BB′∥AO,则旋转角的度数为( )
A. 125° B. 70° C. 55° D. 15°
2.如图,绕点O逆时针旋转得到,若,则等于
A. B. C. D.
3.如图可以看作是一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数可以是
A. B. C. D.
4.如图,将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,连接AD,若∠B=65°,则∠ADE等于( )
A. 30° B. 25° C. 20° D. 15°
5.如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
A. 12 B. 6 C. 6 D.
6.如图,将绕点A按逆时针方向旋转,得到,若点在线段BC的延长线上,则的大小为
A. B. C. D.
7.如图,将绕点O逆时针旋转后得到,若,则的度数是
A. B. C. D.
8.如图,将边长为的正方形ABCD绕点A逆时针方向旋转后得到正方形,则图中阴影部分的面积为
A. B. C. D.
二、填空题
9.如图,在等边三角形ABC中,AC=9,点O在AC上,且AO=3,点P是AB上的一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是________.
10.如图,在中,,,以点C为中心,把逆时针旋转,得到,则图中阴影部分的面积为______.
11.如图,将绕直角顶点C顺时针旋转,得到,连接AD,若,则______.
12.如图,在中,,,点D为BC中点,将绕点D逆时针旋转,得到,与AB交于点E,则______.
13.如图,线段AB两端点坐标分别为、,线段CD两端点坐标分别为、D?数学课外兴趣小组研究这两线段发现:其中一条线段绕着某点旋转一个角度可得到另一条线段,请写出旋转中心的坐标______.
14.如图,等边三角形ABC的边长为9cm,,连接DE,将绕点D逆时针旋转,得到,连接CF,则______cm.
15.如图,在中,,,,现将绕点A逆时针旋转得到,则阴影部分的面积为______.
三、解答题
16.如图所示,将△ABC绕其顶点A顺时针旋转30°后得△ADE.
(1)问△ABC与△ADE的关系如何?
(2)求∠BAD的度数.
17.如图,将Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,若AC⊥A′B′,求∠ABC的度数.
18.如图,△ABC由△EDC绕C点旋转得到,B、C、E三点在同一条直线上,∠ACD=∠B,求证:△ABC是等腰三角形.
19.如图,在正方形ABCD中,E为DC边上的点,连接BE,将绕点C顺时针方向旋转得到,连结EF,若,求的度数.
20.如图,点A′在Rt△ABC的边AB上,与BC交于点D,∠ABC=30°,AC=2,∠ACB=90°,△ACB绕顶点C按逆时针方向旋转与△A′CB′重合,连接BB′,求线段BB′的长度.
21.已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
22.已知:在平面直角坐标系中,点A、B分别在x轴正半轴上,且线段OA、OB(OA<OB)的长分别等于方程的两个根,点C在轴正半轴上,且OB=2OC.
(1)求A、B、C三点坐标;
(2)将△OBC绕点C顺时针旋转90°后得到,求直线的表达式.
参考答案
1.B
【解析】
【分析】
据两直线平行,内错角相等可得,根据旋转的性质可得,然后利用等腰三角形两底角相等可得,即可得到旋转角的度数.
【详解】
,
,
又 ,
中,,
旋转角的度数为.
故选:.
【点睛】
本题考查了旋转的性质,等腰三角形两底角相等的性质,熟记性质并准确识图是解题的关键.
2.C
【解析】
【分析】
根据旋转的性质可知,D和B为对应点,∠DOB为旋转角,即∠DOB=80°,
所以∠AOD=∠DOB﹣∠AOB.
【详解】
根据旋转的性质可知,D和B为对应点,∠DOB为旋转角,即∠DOB=80°,
所以∠AOD=∠DOB﹣∠AOB=80°﹣35°=45°.
故选:C
【点睛】
本题考核知识点:旋转性质. 解题关键点:理解旋转的性质.
3.C
【解析】
【分析】
根据旋转的性质,观察图形,中心角是由8个度数相等的角组成,结合周角是360°,求得每次旋转的度数.
【详解】
中心角是由8个度数相等的角组成,
每次旋转的度数可以为,
故选C.
【点睛】
本题考查了旋转的性质,运用数形结合思想、发现8个相等的中心角构成一个周角是解题的关键.
4.C
【解析】
【详解】
由题意得,∠B=∠CED=65°,AC=DC,
∴∠CAD=∠CDA=45°,
∴∠ADE=∠CED-∠CAD=65-45=20.
故选C.
5.D
【解析】
【分析】
连接B'B,利用旋转的性质和直角三角形的性质解答即可.
【详解】
连接B'B,
∵将△ABC绕点C按逆时针方向旋转得到△A'B'C,
∴AC=A'C,AB=A'B,∠A=∠CA'B'=60°,
∴△AA'C是等边三角形,
∴∠AA'C=60°,
∴∠B'A'B=180°-60°-60°=60°,
∵将△ABC绕点C按逆时针方向旋转得到△A'B'C,
∴∠ACA'=∠BAB'=60°,BC=B'C,∠CB'A'=∠CBA=90°-60°=30°,
∴△BCB'是等边三角形,
∴∠CB'B=60°,
∵∠CB'A'=30°,
∴∠A'B'B=30°,
∴∠B'BA'=180°-60°-30°=90°,
∵∠ACB=90°,∠A=60°,AC=6,
∴AB=12,
∴A'B=AB-AA'=AB-AC=6,
∴B'B=6,
故选D.
【点睛】
此题考查旋转问题,关键是利用旋转的性质和直角三角形的性质解答.
6.B
【解析】
【分析】
由旋转的性质可知,,由等腰三角形的性质和三角形的内角和定理可求得,从而可求得.
【详解】
解:由旋转的性质可知:,,.
,,
.
.
.
故选:B.
【点睛】
本题主要考查的是旋转的性质,由旋转的性质得到为等腰三角形是解题的关键.
7.B
【解析】
【分析】
由已知求出旋转角,再根据角的和差关系求得∠AOE=∠BOE-∠AOB=45?-15?.
【详解】
由已知可得,旋转角:∠BOE=45?,所以,∠AOE=∠BOE-∠AOB=45?-15?=30?.
故选:B
【点睛】
本题考核知识点:旋转角,角的和差倍. 解题关键点:理解旋转角的定义.
8.D
【解析】
【分析】
设BC、C'D'相交于点M,连结AM,根据HL即可证明△AD'M≌△ABM,可得到∠MAB=30°,然后可求得MB的长,从而可求得△ABM的面积,最后利用正方形的面积减去△AD'M和△ABM的面积进行计算即可.
【详解】
设BC、相交于点M,连结AM,
由旋转的性质可知:,
在Rt和Rt△ABM中
,
≌(HL),
,,
,
,
又,
,
,
又,
,
故选D.
【点睛】
本题考查旋转的性质以及全等三角形的判定与性质、特殊锐角三角函数值的应用,熟练掌握相关性质与定理、证得≌是解本题的关键.
9.6
【解析】
【详解】
由题意得,∵∠A+∠APO=∠POD+∠COD,∠A=∠POD=60°,
∴∠APO=∠COD,
在△AOP与△CDO中,
,
∴△AOP≌△CDO(AAS),
∴AP=CO=AC﹣AO=9﹣3=6.
故答案为6.
10.
【解析】
【分析】
先在中利用勾股定理求出,再根据旋转的性质得出≌,然后根据阴影部分的面积扇形的面积的面积的面积扇形的面积,代入数值解答即可.
【详解】
在中,,,
,
把逆时针旋转,得到,
,,,,
阴影部分的面积,
故答案为.
【点睛】
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等也考查了勾股定理以及扇形面积公式的应用.
11.
【解析】
【分析】
根据旋转的性质可得AC=CD,再判断出△ACD是等腰直角三角形,然后根据等腰直角三角形的性质求出∠CAD=45°,由∠BAD=∠BAC+∠CAD可得答案.
【详解】
∵Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC,
∴AC=CD,
∴△ACD是等腰直角三角形,
∴∠CAD=45°,
则∠BAD=∠BAC+∠CAD=25°+45°=70°,
故答案为:70°°.
【点睛】
本题考查了旋转的性质、等腰直角三角形的判定与性质,熟练掌握相关性质并准确识图是解题的关键.
12.28
【解析】
【分析】
利用旋转的性质得出,,进而由求出即可.
【详解】
由题意可得:,,
则,
,
,
,
.
故答案为:28.
【点睛】
考查了旋转的性质以及三角形面积求法,得出是解题关键.
13.或
【解析】
【分析】
分点A的对应点为C或D两种情况考虑:当点A的对应点为点C时,连接AC、BD,分别作线段AC、BD的垂直平分线交于点E,点E即为旋转中心;当点A的对应点为点D时,连接AD、BC,分别作线段AD、BC的垂直平分线交于点M,点M即为旋转中心此题得解.
【详解】
当点A的对应点为点C时,连接AC、BD,分别作线段AC、BD的垂直平分线交于点E,如图1所示:
点的坐标为,B点的坐标为,
点的坐标为;
当点A的对应点为点D时,连接AD、BC,分别作线段AD、BC的垂直平分线交于点M,如图2所示:
点的坐标为,B点的坐标为,
点的坐标为.
综上所述:这个旋转中心的坐标为或.
故答案为:或.
【点睛】
本题考查了坐标与图形变化中的旋转,根据给定点的坐标找出旋转中心的坐标是解题的关键.
14.
【解析】
【分析】
由等边三角形ABC的边长为9cm,可得,,将绕点D逆时针旋转,得到,可得可证为等边三角形,可得,则可得,可得为直角三角形,再根据勾股定理可求CF的长.
【详解】
如图:
是等边三角形
,且,
,是等边三角形.
将绕点D逆时针旋转,得到
,且
,且
为等边三角形
,
,
,
为直角三角形,且,,
,
故答案为
【点睛】
本题考查等边三角形的性质,旋转的性质,直角三角形的判定,勾股定理,本题关键是证明为直角三角形.
15.
【解析】
【分析】
根据旋转的性质可知S△ABC=S△AB1C1,由此可得S阴影=S扇形ABB1,根据扇形面积公式即可得出结论.
【详解】
∵S△ABC=S△AB1C1,
∴S阴影=S扇形ABB1=πAB2=π.
故答案为:π.
【点睛】
本题考查了旋转的性质以及扇形的面积公式,解题的关键是找出S阴影=S扇形ABB1.本题属于基础题,难度不大,解决该题型题目时,根据旋转的性质找出阴影部分的面积等于扇形的面积是关键.
16.(1)△ABC≌△ADE;(2)30°
【解析】由旋转的性质和三角形的性质即可解答.
解:(1)∵△ABC绕其顶点A顺时针旋转30°后得△ADE,∴△ABC≌△ADE.
(2)旋转角相等,即∠BAD=∠EAC=30°.
17.38°.
【解析】分析:
如下图所示,设AC与A′B′的交点为O,则由已知条件易得∠A′OC=90°,∠ACA′=38°,由此可得∠A′=52°,由旋转的性质可得∠A=52°,结合∠ACB=90°即可得到∠ABC=38°.
详解:
∵Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C′,
∴∠ACA′=38°,∠A=∠A′,
∵AC⊥A′B′,
∴∠A′OC=90°,
∴∠A′=90°-38°=52°,
∴∠A=52°,
又∵在Rt△ABC中,∠ACB=90°,
∴∠ABC=180°-90°-52°=38°.
点睛:“由旋转的性质得到∠ACA′=38°,结合AC⊥A′B′得到∠A′=52°=∠A”是解答本题的关键.
18.见解析
【解析】
【分析】
由旋转的性质可知∠D=∠B,再根据已知条件证明AC∥DE,进而证明∠ACB=∠A,所以△ABC是等腰三角形.
【详解】
证明:由旋转知∠D=∠B,
∵∠ACD=∠B,
∴∠ACD=∠D,AC∥DE,
∴∠ACB=∠E,
又∵∠A=∠E,
∴∠ACB=∠A,
∴△ABC是等腰三角形.
【点睛】
本题考查了旋转的性质以及等腰三角形的判定,对于旋转的性质用到最多的是:旋转前、后的图形全等.
19.15°
【解析】
【分析】
根据旋转性质可得:,,,由等腰直角三角形三角形性质可得,所以.
【详解】
解:是旋转得到的图形, ,,, . .
【点睛】
本题考核知识点:旋转性质,等腰直角三角形. 解题关键点:熟记旋转性质,等腰直角三角形性质.
20.BB′=BC=2.
【解析】
【分析】
Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,可得AB=2AC=4,由勾股定理得BC==2;再证△AA′C是等边三角形,得AA′=AB=2,A′C=A′B,可得∠A′CB=∠A′BC=30°,
由旋转得∠A′CB′=90°,BC=B′C,所以∠B′CB=90°﹣30°=60°,证得△BCB′是等边三角形,所以BB′=BC=2.
【详解】
解:∵Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,
∴BC==2,
∵∠A=60°,
∴△AA′C是等边三角形,
∴AA′=AB=2,
∴A′C=A′B,
∴∠A′CB=∠A′BC=30°,
∵△A′B′C是△ABC旋转而成,
∴∠A′CB′=90°,BC=B′C,
∴∠B′CB=90°﹣30°=60°,
∴△BCB′是等边三角形,
∴BB′=BC=2.
【点睛】
本题考核知识点:旋转,直角三角形,等边三角形的判定和性质. 解题关键点:熟记旋转性质和等边三角形的判定和性质.
21.(1)证明见解析;(2)5.
【解析】
【分析】
(1)直接利用旋转的性质可得AP=AQ,∠PAQ=60°,然后根据“SAS”证明△BAP≌△CAQ,结合全等三角形的性质得出答案;
(2)由△APQ是等边三角形可得AP=PQ=3,∠AQP=60°,由全等的性质可得∠AQC =∠APB=150°,从而可求∠PQC=90°,然后根据勾股定理求PC的长即可.
直接利用等边三角形的性质结合勾股定理即可得出答案.
【详解】
(1)证明:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中
,
∴△BAP≌△CAQ(SAS),
∴PB=QC;
(2)解:∵由(1)得△APQ是等边三角形,
∴AP=PQ=3,∠AQP=60°,
∵∠APB=150°,
∴∠PQC=150°﹣60°=90°,
∵PB=QC,
∴QC=4,
∴△PQC是直角三角形,
∴PC===5.
【点睛】
本题考查了旋转的性质,等边三角形的性质与判定,全等三角形的判定与性质,勾股定理.证明△BAP≌△CAQ是解(1)的关键,证明∠PQC=90°是解(2)的关键.
22.(1) A(1,0)、B(4,0)、 C(0,2); (2)
【解析】
【分析】
(1)先利用因式分解法解方程x2-5x+4=0可确定A(1,0)、B(4,0);再利用OB=2OC,且点C在y轴正半轴上可确定C点坐标;
(2)利用旋转的性质得OB=O′B′=4,OC=O′C′=2,∠COB=∠C0′B′=90°,∠OCO′=∠BCB′=90°,则可确定O′(-2,2)、B′(-2,-2),然后利用待定系数法求直线B′C的解析式.
【详解】
(1) ∵OA、OB的长是方程2-5+4=0的两个根,且OA<OB,
解得
∴OA=1,OB=4
∵A、B分别在x轴正半轴上,
∴A(1,0)、B(4,0)
又∵OB2OC,且点C在轴正半轴上
∴OC2,C(0,2)
(2) ∵ 将△OBC绕点C顺时针旋转90°后得到
∴OB=O′B′=4,OC=O′C′=2,∠COB=∠C0′B′=90°,∠OCO′=∠BCB′=90°
∴O′(-2,2)、B′(-2,-2)
设直线B′C的解析式为
∴,解得
∴直线B′C的解析式为.
【点睛】本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了旋转的性质和待定系数法求一次函数解析式.
同课章节目录
