23.1 图形的旋转同步课时作业（3）

中小学教育资源及组卷应用平台
23.1 图形的旋转同步课时作业（3）
姓名：___________班级：___________考号：___________
一、选择题
1．在俄罗斯方块游戏中，已拼好的图案如图所示，现又出现一小方格体正向下运动，为了使所有图案消失，你必须进行以下哪项操作，才能拼成一个完整图案，使其自动消失（　　）
A． 顺时针旋转90°，向右平移 B． 逆时针旋转90°，向右平移
C． 顺时针旋转90°，向下平移 D． 逆时针旋转90°，向下平移
2．（2017届湖南省娄底市九年级中考一模数学试卷）将数字“6”旋转180°，得到数字“9”，将数字“9”旋转180°，得到数字“6”，现将数字“69”旋转180°，得到的数字是（ ）
A． 96 B． 69 C． 66 D． 99
3．如图所示的图案是由六个全等的菱形拼成的，它也可以看作是以一个图案为“基本图案”，通过旋转得到的．以下图案中，不能作为“基本图案”的一个是( )
4．如图，四边形ABCD为正方形，点O为AC、BD的交点，则三角形COD绕点O经过下列哪种旋转可以得到三角形DOA（　　）
A． 顺时针旋转45° B． 顺时针旋转90° C． 逆时针旋转45° D． 逆时针旋转90°
5．在图中，将左边方格纸中的图形绕O点顺时针旋转90°得到的图形是（ ）
A． B． C． D．
6．如图，下列图形经过旋转后，与左下图相同的是（　　）
A． B． C． D．
7．如图，四边形ABCD的顶点坐标A（﹣3，6）、B（﹣1，4）、C（﹣1，3）、D（﹣5，3）．若四边形ABCD绕点C按顺时针方向旋转90°，再向左平移2个单位，得到四边形A′B′C′D′，则点A的对应点A′的坐标是（ ）
A． （0，5） B． （4，3） C． （2，5） D． （4，5）
8．如图所示，该图案是经过( )
A． 平移得到的 B． 旋转或轴对称得到的 C． 轴对称得到的 D． 旋转得到的
二、填空题
9．我国国旗上的四个小五角星，通过_______________移动可以相互得到．
10．如图，将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形，至少需要移动　 　格．
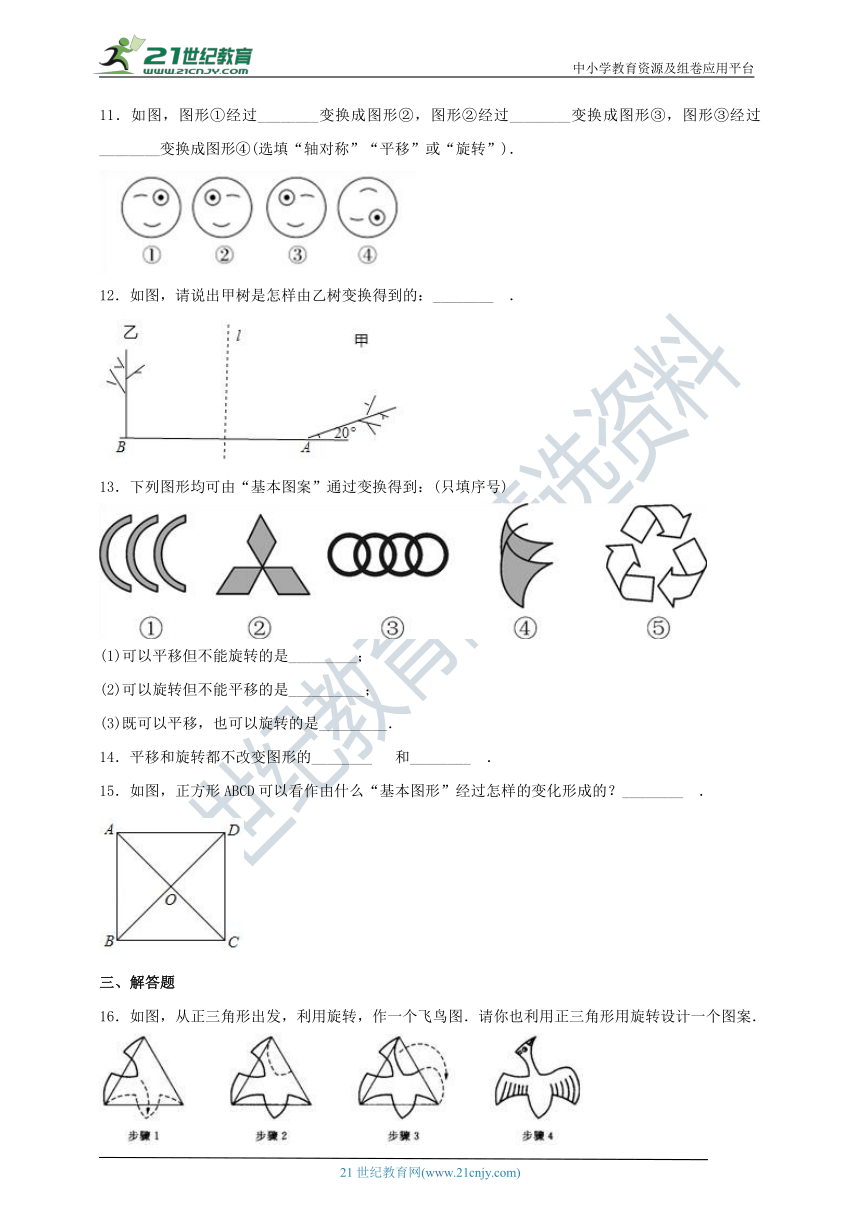
11．如图，图形①经过________变换成图形②，图形②经过________变换成图形③，图形③经过________变换成图形④(选填“轴对称”“平移”或“旋转”)．
12．如图，请说出甲树是怎样由乙树变换得到的：________ ．
13．下列图形均可由“基本图案”通过变换得到：(只填序号)
(1)可以平移但不能旋转的是_________；
(2)可以旋转但不能平移的是__________；
(3)既可以平移，也可以旋转的是_________．
14．平移和旋转都不改变图形的________ 和________ ．
15．如图，正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的？________ ．
三、解答题
16．如图，从正三角形出发，利用旋转，作一个飞鸟图．请你也利用正三角形用旋转设计一个图案．
17．如图，网格中每个小正方形的边长为1，点C（0，1），点B（-1，3）．
（1）利用网格画出直角坐标系（要求标出x轴，y轴和原点），则点A的坐标为_________；
（2）以△ABC为基本图形，利用旋转设计一个图案，说明你的创意为__________________．
18．如图所示的正方形网格中，△ABC 的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：
（1）以A点为旋转中心，将△ABC绕点A顺时针旋转90°得△AB1C1，画出△AB1C1.
（2）作出△ABC关于坐标原点O成中心对称的△A2B2C2.
（3）作出点C关于x轴的对称点P. 若点P向右平移x个单位长度后落在△A2B2C2的内部(不含落在△A2B2C2的边上)，请直接写出x的取值范围．
（提醒：每个小正方形边长为1个单位长度）
19．在如图所示的方格纸中，每个小方格都是边长为1个单位的正方形，图①、图②、图③均为顶点都在格点上的三角形（每个小方格的顶点叫格点），
（1）在图1中，图①经过一次　　变换（填“平移”或“旋转”或“轴对称”）可以得到图②；
（2）在图1中，图③是可以由图②经过一次旋转变换得到的，其旋转中心是点　　（填“A”或 “B”或“C”）；
（3）在图2中画出图①绕点A顺时针旋转90°后的图④.
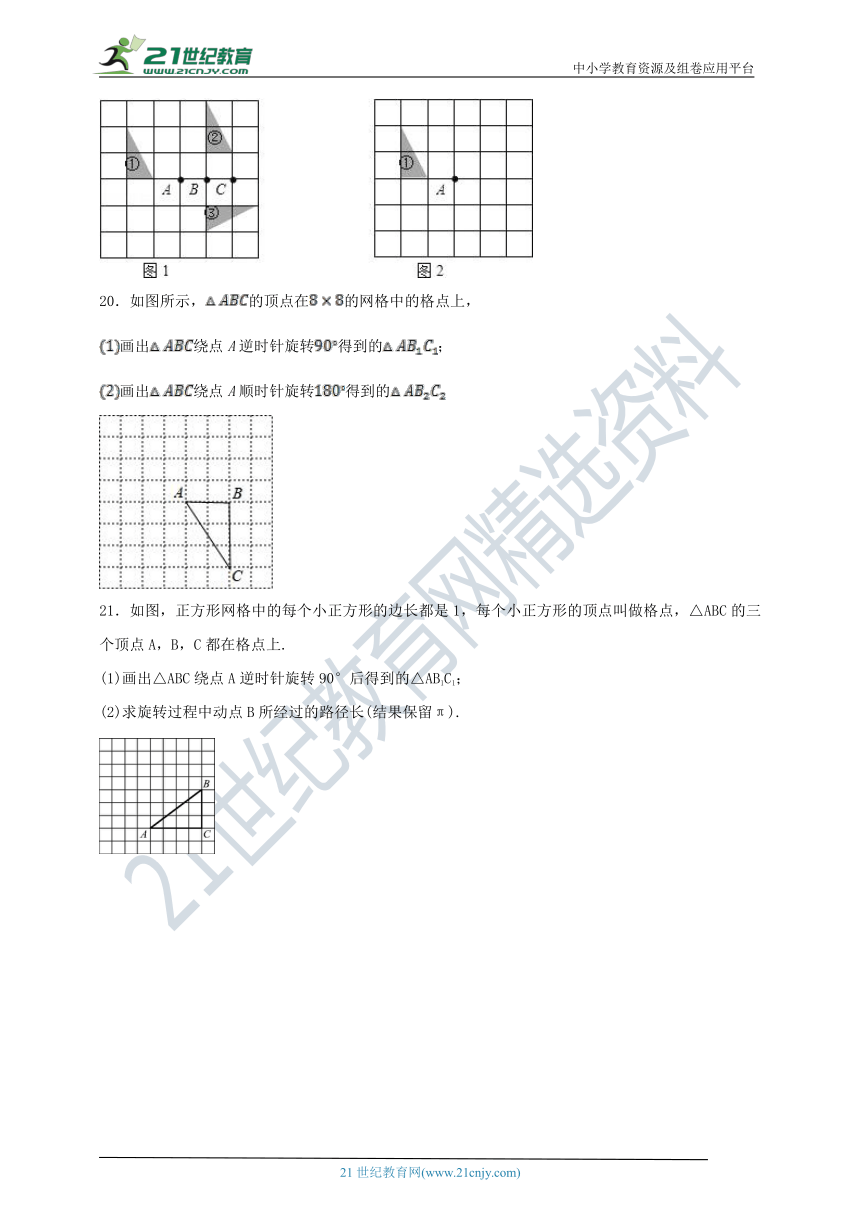
20．如图所示，的顶点在的网格中的格点上，
画出绕点A逆时针旋转得到的；
画出绕点A顺时针旋转得到的
21．如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点，△ABC的三个顶点A，B，C都在格点上.
(1)画出△ABC绕点A逆时针旋转90°后得到的△AB1C1；
(2)求旋转过程中动点B所经过的路径长(结果保留π).
参考答案
1．A
【解析】分析：运用旋转和平移性质可得.
详解：由已知可得，顺时针旋转90°，向右平移，能把右下角完全填补.只有选项A符合条件，其他选项不能符合条件.
故选：A.
点睛：本题考核知识点：旋转和平移.解题关键点：理解旋转性质和平移性质，同时理解游戏规则即可.
2．B
【解析】现将数字“69”旋转180°，得到的数字是：69，
故选B．
3．B
【解析】试题分析：A、顺时针，连续旋转60度，三次即可得到．
B、不能作为“基本图案”．
C、旋转180度，即可得到．
D、旋转60度即可．
故选B．
点睛：本题考查了图形的旋转变化，认真观察旋转得到的图案，找到旋转中心，即可判断．
4．D
【解析】
【分析】
逆时针旋转90° ,可得结果.
【详解】
逆时针旋转90°，可以得到三角形DOA.故选D.
【点睛】
在平面内，把一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转。点O叫做旋转中心，旋转的角叫做旋转角，如果图形上的点P经过旋转变为点Pˊ，那么这两个点叫做这个旋转的对应点.
5．B
【解析】分析：根据旋转的性质，找出图中三角形的关键处（旋转中心）按顺时针方向旋转90°后的形状即可选择答案．
详解：根据旋转的性质可知，绕O点顺时针旋转90°得到的图形是 ．
故选B．
点睛：本题考查了旋转的性质．旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．
6．D
【解析】试题解析：旋转只是改变图形的位置，不改变图形的形状与大小，据此得：
A，B，C与原来的图形形状不同，只有D相同，
故选D．
7．A
【解析】旋转、平移后四边形如图所示,
A'的坐标为,
故选A.
8．B
【解析】根据图案的形状可知：通过旋转和轴对称折叠旋转即可得到，因此可知B答案正确.
故选：B.
9．旋转或旋转和平移
【解析】解：四个小五角星通过旋转可以互相得到．故答案为：旋转．
10．9
【解析】
试题分析：要使平移的个数最少，可将它们朝同一方向共同移动，此时需要平移的格数最少．
解：如图，将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形，
根据平移的基本性质知：左边的线段向右平移3格，中间的线段向下平移2格，最右边的线段先向左平移2格，再向上平移2格，此时平移的格数最少为：3+2+2+2=9，
其它平移方法都超过9格，
∴至少需要移动9格．
考点：平移的性质．
点评：本题考查平移的基本概念及平移规律，是比较简单的几何图形变换．关键是要观察比较平移前后物体的位置．
11． 轴对称,　 平移　, 旋转
【解析】试题解析：图形（1）经过轴对称变换成图形（2），图形（2）经过平移变换成图形（3），图形（3）经过旋转变换成图形（4）．
故答案为：轴对称,平移,旋转.
12．先以直线L为对称轴作轴对称变换，再把所得的像绕点A顺时针旋转70度
【解析】试题分析：由图易知A，B关于直线l对称，那么可先以直线l为对称轴作轴对称变换，得到与地面垂直的图形，最后的图形与地面的夹角是20°，所以应把所得的图象绕点A顺时针旋转70度．
故答案为：先以直线l为对称轴作轴对称变换，再把所得的像绕点A顺时针旋转70度．
点睛：旋转是绕某个点旋转一定角度得到新图形，轴对称是沿某条直线翻折得到新图形．观察时要紧扣图形变换特点，认真判断．
13． ①④ ②⑤ ③
【解析】试题分析：①可以看作由左边图案向右平移得到的；
②可以看作一个菱形绕一个顶点旋转得到的；
③既可以看作一个圆向右平移得到的，也可以看作两个圆组成的图案旋转得到的；
④可以看作上面基本图案向下平移得到的；
⑤可以看作上面图案绕中心旋转得到的．
故可以平移但不能旋转的是①④；
可以旋转但不能平移的是②⑤；
既可以平移，也可以旋转的是③．
故答案为（1）①④，（2）②⑤，（3）③
14． 形状； 大小
【解析】平移和旋转都不改变图形的形状和大小．
故答案为：形状，大小．
15．把△ABO绕O点连续旋转90°，180°，270°可以得到正方形ABCD
【解析】观察图形可知把△ABO绕O点连续旋转90°，180°，270°可以得到正方形ABCD．
故答案为：把△ABO绕O点连续旋转90°，180°，270°可以得到正方形ABCD．
16．图案见解析.
【解析】试题分析：
先以等边三角形的一边为基础画一个基本图形，再绕等边三角形的两个顶点分别旋转60°后删除原等边三角形即可.
试题解析：
如图所示：
点睛：本题考查了等边三角形的性质和旋转的性质，旋转是全等变换，旋转只改变图形的位置，不改变图形的大小和形状，以等边三角形为依托设计图案时，只需要先以等边三角形的一边为基础设计一个基本图形，再以等边三角形的顶点为旋转中心，旋转60°后构成一个整体.
17． A(-4,3) 见解析.
【解析】试题分析：
（1）根据点C的坐标确定原点，则可以画出直角坐标系，把点B向左平移3个单位长度得到点A；
（2）把△ABC绕点C顺时针旋转3次，即可得到一个风车的图案.
试题解析：
（1）直角坐标系如图所示，则A的坐标为（-4，3）；
（2）如图，把△ABC绕点C顺时针旋转3次90°，180°，270°，即可得到一个风车的图案.
18．（1）作图见解析；（2）作图见解析；（3）5.5【解析】（1）利用网络特点和旋转的性质画出点B、C的对应点B1、C1，则可得到△AB1C1；
（2）根据关于原点 的点的坐标特征写出点A2、B2、C2的坐标，然后描点即可得到△A2B2C2；
（3）先利用关于x轴的对称点的坐标特征写出P点坐标，再描点得到P点，然后观察图形可判断x的取值范围.
⑴如图△AB1C1为所作；
（2）如图△A2B2C2为所作；
（3）5.5“点睛”本题考查了作图-旋转变换：根据旋转的性质可知，对应角相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形，也考查另外平移变换.
19．（1）平移；（2）A；（3）作图见解析.
【解析】试题分析：（1）根据平移的定义可知图①向右上平移可以得到图②；
（2）将图形②绕着点A旋转后能与图形③重合，可知旋转中心；
（3）以A为旋转中心，顺时针旋转90°得到关键顶点的对应点连接即可．
试题解析：（1）图①经过一次平移变换可以得到图②；
（2）图③是可以由图②经过一次旋转变换得到的，其旋转中心是点A；
（3）如图．
【点睛】本题难度中等，考查网格中平移、旋转及旋转作图，作图时，抓住网格的特点，根据旋转的性质，借助于直角三角板中的直角，就能顺利作出图形，解题时要注意是顺时针还是逆时针方向．
平移是沿直线移动一定距离得到新图形，旋转是绕某个点旋转一定角度得到新图形，观察时要紧扣图形变换特点，认真判断．
20．（1）作图见解析；（2）作图见解析.
【解析】
【分析】
利用网格特点和旋转的性质画出点B、C的对应点、得到；
利用网格特点和旋转的性质画出点B、C的对应点、得到．
【详解】
解：如图，为所作；
如图，为所作．
【点睛】
本题考查了作图旋转变换.根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
21．(1)画图见解析；(2)点B所经过的路径长为.
【解析】
【分析】
(1)让三角形的顶点B、C都绕点A逆时针旋转90°后得到对应点,顺次连接即可.
(2)旋转过程中点B所经过的路线是一段弧,根据弧长公式计算即可.
【详解】
(1)如图.
(2)由(1)知这段弧所对的圆心角是90°,半径AB==5,
∴点B所经过的路径长为.
【点睛】
本题主要考查了作旋转变换图形，勾股定理，弧长计算公式，熟练掌握旋转的性质和弧长的计算公式是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)