简谐运动的回复力和能量
图片预览

文档简介
第十一章 机械振动
第三节 简谐运动的回复力和能量
教材分析
这一节是本章中第三节内容,教材从人对事物的认知规律出发,安排前两节内容从简谐运动的运动特征进行的分析,本节内容从动力学的角度分析解决了为什么做这种运动的问题,同时还从能量的角度进行了进一步的研究。因此,如何引导学生从动力学和能量的角度进行研究是本节课的重点,从这两个研究角度入手,使学生形成对回复力的理解和振动形成原因的认识是学习的难点所在。
学情分析
前面的学习中,学生学习了动力学和能量的一些基础知识,通过直线运动,曲线运动中的平抛和圆周运动这些不同的运动类型的学习,建立了力与运动关系的认识。对新的运动类型,让学生分析其受力特征,从而理解此类运动的形成原因,对学生的能力要求较高,需要教师合理引导,将难点分解。
一、教学目标
1、知识与技能
(1)理解回复力的概念。
(2)学会用动力学的方法,分析简谐运动中位移、速度、回复力和加速度的变化规律。
(3)学会用能量守恒的观点,分析水平弹簧振子中动能、弹性势能、总能量的变化规律。
2、过程与方法
(1)通过对简谐运动中运动过程的分析理解回复力的特点,体会动力学方法分析物体运动的基本思路,提高学生分析和解决问题的能力。
(2)通过研究简谐运动中能量的变化掌握分析运动过程中能量转化的基本方法。
3、情感、态度与价值观
(1)通过对简谐运动中回复力的分析培养学生的分析综合能力。
(2)通过对回复力的学习使学生体会复杂的运动形式中所蕴含的简单的受力特征,激发学生从复杂的事物现象中揭示简单的物理本质的学习兴趣。
(3)从简谐运动过程中能量的相互转化情况,对学生进行物质世界遵循对立统一规律观点的渗透
二、教学重点
1、理解简谐运动中的回复力
2、分析简谐运动中能量的转化情况,理解能量的变化规律
三、教学难点
简谐运动中回复力的理解及振动形成原因的认识。
四、教学器材
水平弹簧振子、水槽和木块、圆弧形凹槽和钢球、多媒体课件
五、教学过程
新课导入:
演示实验,提醒学生仔细观察,水平弹簧振子的振动、水槽中木块的上下浮动、圆弧形凹槽中钢球的的滚动,
学生可能观察到的结果:往复运动、周期性运动、运动速度快慢周期性变化、 最终都停在某一位置、有对称性等等。
教师讲解设疑,引入主题:
首先肯定学生的观察,这几个运动都是简谐运动,从运动形式上看,简谐运动是物体在某一平衡位置附近的往复周期性的运动。做简谐运动的物体为何有这样的运动形式呢?
新课教学:
教师引导学生思考:力是改变物体运动的原因,做简谐运动的物体之所以有这样的运动形式,与其受力特征一定有关,做简谐运动的物体其受力又如何?
以水平弹簧振子为研究对象,学生观察思考其受力的特征。
教师引导学生首先进行受力分析,思考弹力的作用就是让小球回到平衡位置,引出回复力的概念:
【板书】1. 简谐运动的回复力
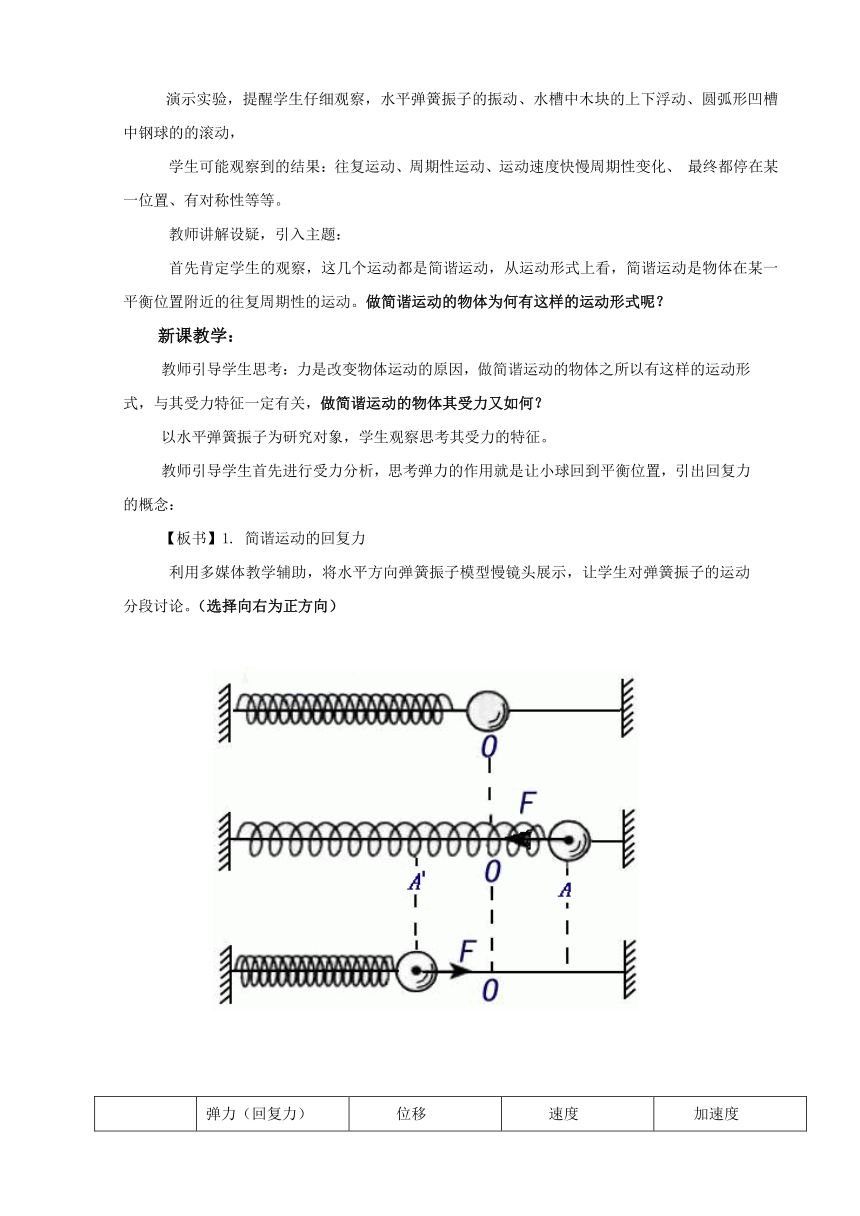
利用多媒体教学辅助,将水平方向弹簧振子模型慢镜头展示,让学生对弹簧振子的运动分段讨论。(选择向右为正方向)
弹力(回复力) 位移 速度 加速度
方向 大小 方向 大小 方向 大小 方向 大小
A - O - ↓ + ↓ - ↑ - ↓
O – A’ + ↑ - ↑ - ↓ + ↑
A’- O + ↓ - ↓ + ↑ + ↓
O - A - ↑ + ↑ + ↓ - ↑
让学生完成以上表格
通过上表的分析得出弹簧振子振动时,回复力与位移的方向关系;又根据胡克定律,弹簧振子的回复力与位移成正比。归纳得出回复力与位移的关系
【板书】
物体在跟位移大小成正比,并且总指向平衡位置的力作用下的振动,叫做简谐运动。
式中F为回复力;x为偏离平衡位置的位移;k是常数,对于弹簧振子,k是劲度系数,对于其它物体的简谐运动,k是别的常数;负号表示回复力与位移的方向总相反。
提 问:如何判断振动是否是简谐运动?
学生回答:判断回复力是否具有这种特征。
弹簧振子的振动只是简谐运动的一种。弹簧振子在振动中,小球的速度在变化,所以小球的动能也在变。弹簧的长度在变化,因而弹性势能也在变,它们的变化存在哪些规律呢?
【板书】2.简谐运动的能量
利用课件展示水平弹簧振子在外力作用下把它拉伸,松手后所做的简谐运动。(不计阻力),
组织学生分析讨论弹簧振子和单摆在振动中的能量转化情况,并填入表格。
振子的运动 A→O O→B B→O O→A
位移的大小 减小 增大 减小 增大
速度的大小 增大 减小 增大 减小
能量的变化 动能 增大 减少 增大 减少
势能 减少 增大 减少 增大
总能 不变 不变 不变 不变
教师归纳总结:
通过上图我们可以归纳出这样一个结论,在弹簧振子这个简谐振动模型中,弹簧振子的弹性势能和动能间发生相互转换,而任意时刻,系统总的机械能是守恒的。
【课堂练习】
例题:证明以下几个物体为谐振子:1.证明漂浮在水面的木块为谐振子。
(已知ρ水,ρ木,木块的横截面积S)
课堂小结:
通过本节课的学习,我们知道了:
1. 物体在跟位移大小成正比,并且总指向平衡位置的力作用下的振动,叫做简谐运动。判断一个物体是否是简谐运动就在于分析其回复力是否满足F=-kx
2.在简谐运动中,忽略能量的损失,动能与势能间相互转化,而总的机械能是守恒的。
课后思考练习:
练习题1.竖直悬挂的弹簧振子(已知弹簧的劲度系数K)
此题课拓展引申为:悬挂在光滑斜面上的弹簧振子(已知弹簧的劲度系 数K)
练习题2.式分析证明光滑弧面凹槽内小球的运动(小球的位移远小于圆弧面半径)也是简谐运动,并由此模型分析:回复力一定是振子受到的合力吗?
A
B
O
第三节 简谐运动的回复力和能量
教材分析
这一节是本章中第三节内容,教材从人对事物的认知规律出发,安排前两节内容从简谐运动的运动特征进行的分析,本节内容从动力学的角度分析解决了为什么做这种运动的问题,同时还从能量的角度进行了进一步的研究。因此,如何引导学生从动力学和能量的角度进行研究是本节课的重点,从这两个研究角度入手,使学生形成对回复力的理解和振动形成原因的认识是学习的难点所在。
学情分析
前面的学习中,学生学习了动力学和能量的一些基础知识,通过直线运动,曲线运动中的平抛和圆周运动这些不同的运动类型的学习,建立了力与运动关系的认识。对新的运动类型,让学生分析其受力特征,从而理解此类运动的形成原因,对学生的能力要求较高,需要教师合理引导,将难点分解。
一、教学目标
1、知识与技能
(1)理解回复力的概念。
(2)学会用动力学的方法,分析简谐运动中位移、速度、回复力和加速度的变化规律。
(3)学会用能量守恒的观点,分析水平弹簧振子中动能、弹性势能、总能量的变化规律。
2、过程与方法
(1)通过对简谐运动中运动过程的分析理解回复力的特点,体会动力学方法分析物体运动的基本思路,提高学生分析和解决问题的能力。
(2)通过研究简谐运动中能量的变化掌握分析运动过程中能量转化的基本方法。
3、情感、态度与价值观
(1)通过对简谐运动中回复力的分析培养学生的分析综合能力。
(2)通过对回复力的学习使学生体会复杂的运动形式中所蕴含的简单的受力特征,激发学生从复杂的事物现象中揭示简单的物理本质的学习兴趣。
(3)从简谐运动过程中能量的相互转化情况,对学生进行物质世界遵循对立统一规律观点的渗透
二、教学重点
1、理解简谐运动中的回复力
2、分析简谐运动中能量的转化情况,理解能量的变化规律
三、教学难点
简谐运动中回复力的理解及振动形成原因的认识。
四、教学器材
水平弹簧振子、水槽和木块、圆弧形凹槽和钢球、多媒体课件
五、教学过程
新课导入:
演示实验,提醒学生仔细观察,水平弹簧振子的振动、水槽中木块的上下浮动、圆弧形凹槽中钢球的的滚动,
学生可能观察到的结果:往复运动、周期性运动、运动速度快慢周期性变化、 最终都停在某一位置、有对称性等等。
教师讲解设疑,引入主题:
首先肯定学生的观察,这几个运动都是简谐运动,从运动形式上看,简谐运动是物体在某一平衡位置附近的往复周期性的运动。做简谐运动的物体为何有这样的运动形式呢?
新课教学:
教师引导学生思考:力是改变物体运动的原因,做简谐运动的物体之所以有这样的运动形式,与其受力特征一定有关,做简谐运动的物体其受力又如何?
以水平弹簧振子为研究对象,学生观察思考其受力的特征。
教师引导学生首先进行受力分析,思考弹力的作用就是让小球回到平衡位置,引出回复力的概念:
【板书】1. 简谐运动的回复力
利用多媒体教学辅助,将水平方向弹簧振子模型慢镜头展示,让学生对弹簧振子的运动分段讨论。(选择向右为正方向)
弹力(回复力) 位移 速度 加速度
方向 大小 方向 大小 方向 大小 方向 大小
A - O - ↓ + ↓ - ↑ - ↓
O – A’ + ↑ - ↑ - ↓ + ↑
A’- O + ↓ - ↓ + ↑ + ↓
O - A - ↑ + ↑ + ↓ - ↑
让学生完成以上表格
通过上表的分析得出弹簧振子振动时,回复力与位移的方向关系;又根据胡克定律,弹簧振子的回复力与位移成正比。归纳得出回复力与位移的关系
【板书】
物体在跟位移大小成正比,并且总指向平衡位置的力作用下的振动,叫做简谐运动。
式中F为回复力;x为偏离平衡位置的位移;k是常数,对于弹簧振子,k是劲度系数,对于其它物体的简谐运动,k是别的常数;负号表示回复力与位移的方向总相反。
提 问:如何判断振动是否是简谐运动?
学生回答:判断回复力是否具有这种特征。
弹簧振子的振动只是简谐运动的一种。弹簧振子在振动中,小球的速度在变化,所以小球的动能也在变。弹簧的长度在变化,因而弹性势能也在变,它们的变化存在哪些规律呢?
【板书】2.简谐运动的能量
利用课件展示水平弹簧振子在外力作用下把它拉伸,松手后所做的简谐运动。(不计阻力),
组织学生分析讨论弹簧振子和单摆在振动中的能量转化情况,并填入表格。
振子的运动 A→O O→B B→O O→A
位移的大小 减小 增大 减小 增大
速度的大小 增大 减小 增大 减小
能量的变化 动能 增大 减少 增大 减少
势能 减少 增大 减少 增大
总能 不变 不变 不变 不变
教师归纳总结:
通过上图我们可以归纳出这样一个结论,在弹簧振子这个简谐振动模型中,弹簧振子的弹性势能和动能间发生相互转换,而任意时刻,系统总的机械能是守恒的。
【课堂练习】
例题:证明以下几个物体为谐振子:1.证明漂浮在水面的木块为谐振子。
(已知ρ水,ρ木,木块的横截面积S)
课堂小结:
通过本节课的学习,我们知道了:
1. 物体在跟位移大小成正比,并且总指向平衡位置的力作用下的振动,叫做简谐运动。判断一个物体是否是简谐运动就在于分析其回复力是否满足F=-kx
2.在简谐运动中,忽略能量的损失,动能与势能间相互转化,而总的机械能是守恒的。
课后思考练习:
练习题1.竖直悬挂的弹簧振子(已知弹簧的劲度系数K)
此题课拓展引申为:悬挂在光滑斜面上的弹簧振子(已知弹簧的劲度系 数K)
练习题2.式分析证明光滑弧面凹槽内小球的运动(小球的位移远小于圆弧面半径)也是简谐运动,并由此模型分析:回复力一定是振子受到的合力吗?
A
B
O
