14.3.2 公式法 课件 (共26张PPT)
文档属性
| 名称 | 14.3.2 公式法 课件 (共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 457.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-06 21:45:12 | ||
图片预览




文档简介
课件26张PPT。第十四章 整式的乘法和因式分解14.3 因式分解
第二课时 14.3.2 公式法掌握用平方差公式分解因式的方法,熟练运用平方差公式分解因式。
掌握用完全平方公式分解因式的方法,熟练运用平方差公式分解因式。
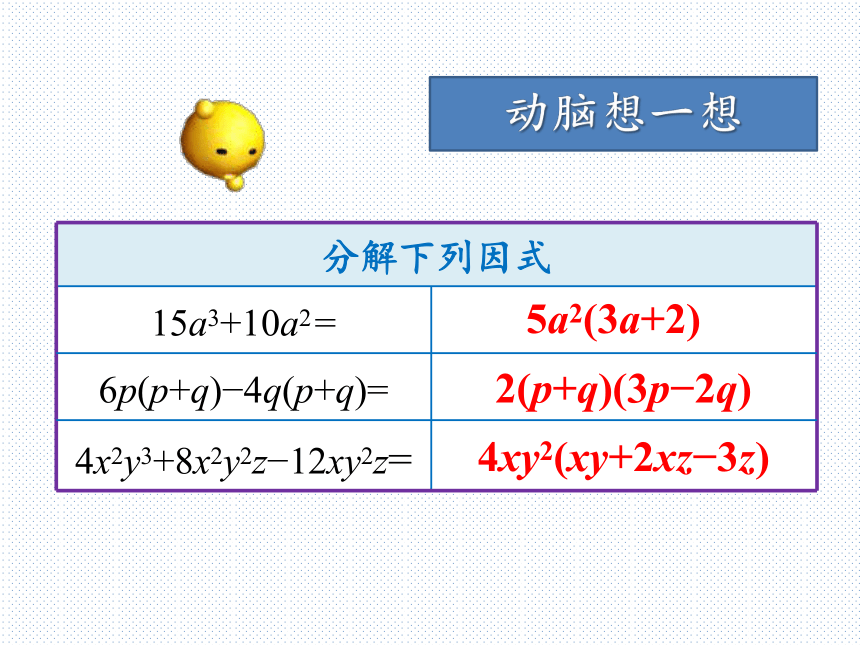
进一步理解因式分解的概念。动脑想一想5a2(3a+2)2(p+q)(3p?2q)4xy2(xy+2xz?3z)观察下面的多项式,它们有什么特点?
x2?4
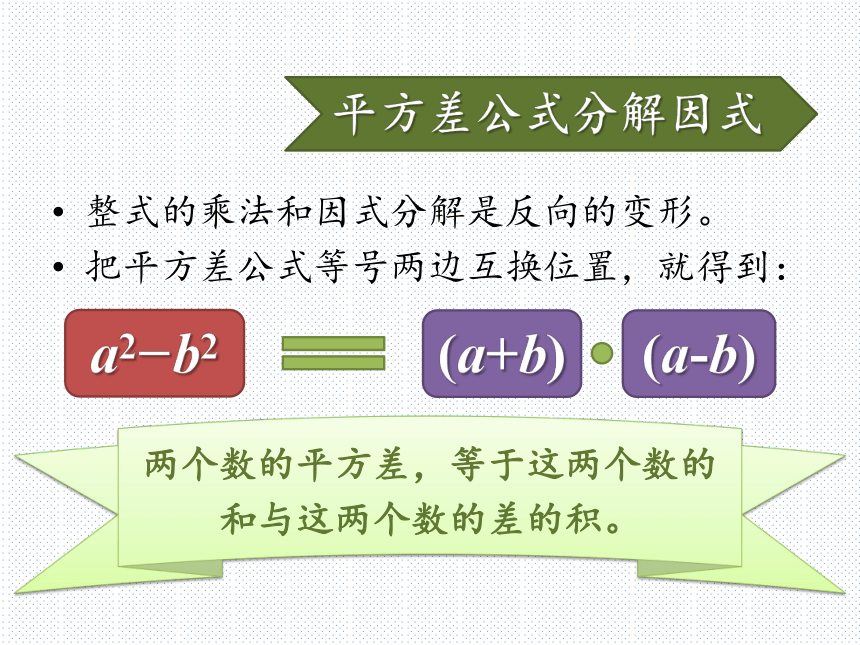
y2?25动脑想一想回忆之前的平方差公式,你能把这些多项式分解因式吗?x2?22y2?52a2?b2平方差公式分解因式整式的乘法和因式分解是反向的变形。
把平方差公式等号两边互换位置,就得到:(a+b)a2?b2(a-b)两个数的平方差,等于这两个数的和与这两个数的差的积。动脑想一想(x+2)(x?2)(y+5)(y?5)a2-b2 =(a+b)(a-b)解:原式=(2x)2?32
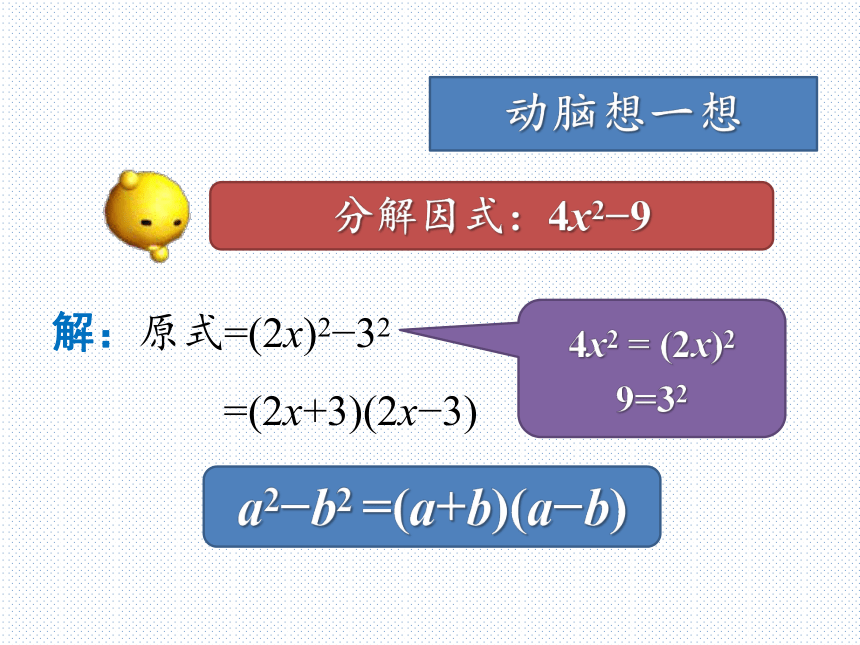
=(2x+3)(2x?3)动脑想一想分解因式:4x2?94x2 = (2x)2
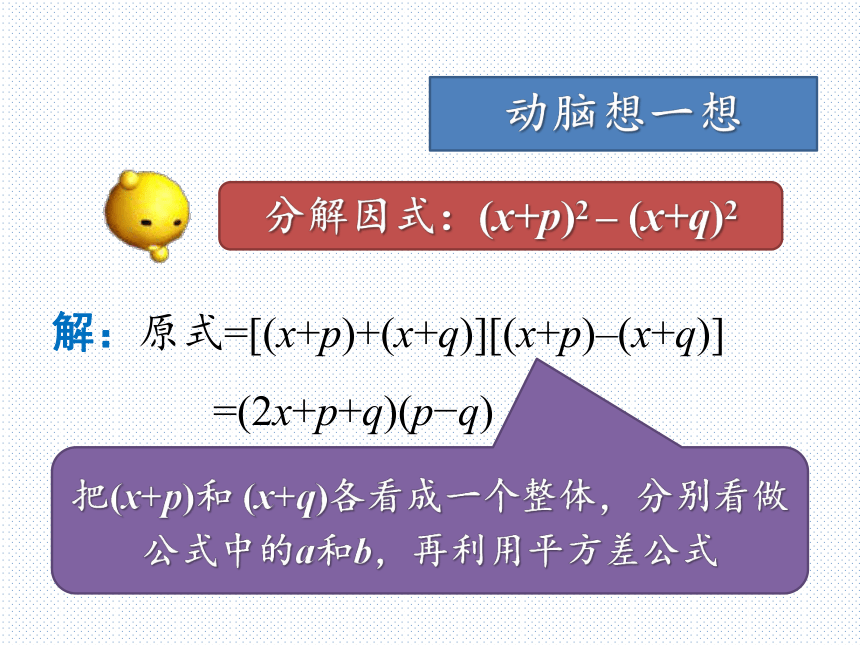
9=32a2?b2 =(a+b)(a?b)解:原式=[(x+p)+(x+q)][(x+p)–(x+q)]
=(2x+p+q)(p?q)动脑想一想分解因式:(x+p)2 – (x+q)2把(x+p)和 (x+q)各看成一个整体,分别看做公式中的a和b,再利用平方差公式解:原式=(x2+y2)(x2?y2)
=(x2+y2)(x+y)(x?y)
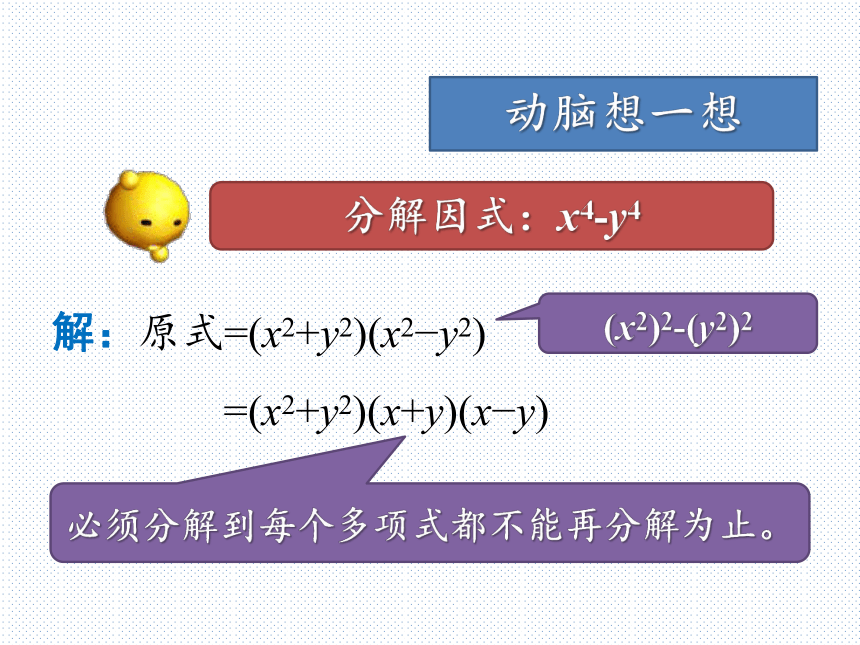
动脑想一想分解因式:x4-y4必须分解到每个多项式都不能再分解为止。(x2)2-(y2)2解:原式=ab(a2?1)
=ab(a+1)(a?1)动脑想一想分解因式:a3b – ab进一步用平方差公式进行分解。先提公因式观察下面的多项式,它们有什么特点?
x2?4x+4
y2+2x+1动脑想一想你还记得你在哪里见过类似这样的式子吗?x2?2·2x+22y2+2·1x+12a2±2ab+b2完全平方式形如下式的,带有两个同号平方项的二次三项式,叫做完全平方式:首平方,尾平方,首尾两倍在中央。a2±2ab+b2?动脑想一想是是不是不是是怎样把完全平方式因式分解呢?完全平方公式因式分解把完全平方公式等号两边互换,就得到:(a±b)2a2±2ab+b2两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方。动脑想一想(x?2)2(y+1)2a2±2ab+b =(a±b)2解:原式=(4x)2+2·4x·3+32
=(4x+3)2动脑想一想分解因式:16x2+24x+916x2=(4x)2
9=32
24x=2·4x·3a2±2ab+b =(a±b)2解:原式=?(x2?4xy+4y2)
=?[x2?2·x·2y+(2y)2]
=?(x?2y)2 动脑想一想分解因式: –x2+4xy–4y2先把首项的负号提出去,便于观察解:原式=3a(x2+2xy+y2)
=3a(x+y)2
动脑想一想分解因式:3ax2+6axy+3ay2有公因式3a,先提出来公因式,再进一步分解。解:原式=(a+b)2?2·(a+b)·6+62
=(a+b?6)2
动脑想一想分解因式:(a+b)2-12(a+b)+36把(a+b)看成一个整体,可看做完全平方式。小结:公式法分解因式把乘法公式的等号两端互换位置,就可以得到用来分解因式的公式,这就是公式法分解因式。a2±2ab+b =(a±b)2a2?b2 =(a+b)(a?b)学完本节课你应该知道公式法完全平方式完全平方公式把一个多项式化成几个整式的积因式分解平方差公式a2?b2 =(a+b)(a?b)a2±2ab+b2a2±2ab+b =(a±b)2动笔练一练下列式子中,可以用平方差公式因式分解的是 。
①x2+y2 ②x2-y2 ③-x2+y2 ④-x2-y2
下列式子中是完全平方式的是 。
①a2-4a+4 ②1+4a2 ③4b2+4b-1 ④a2+ab+b2② ③① ③动笔练一练(3a+2b)(3a?2b)y(x+2)(x-2)?(4+a2)(2+a)(2?a)动笔练一练?(x+y)2(2x?1)2a(a+x)2?3(x?y)2课后练一练请同学们独立完成配套课后练习题。下课!谢谢同学们!
掌握用完全平方公式分解因式的方法,熟练运用平方差公式分解因式。
进一步理解因式分解的概念。动脑想一想5a2(3a+2)2(p+q)(3p?2q)4xy2(xy+2xz?3z)观察下面的多项式,它们有什么特点?
x2?4
y2?25动脑想一想回忆之前的平方差公式,你能把这些多项式分解因式吗?x2?22y2?52a2?b2平方差公式分解因式整式的乘法和因式分解是反向的变形。
把平方差公式等号两边互换位置,就得到:(a+b)a2?b2(a-b)两个数的平方差,等于这两个数的和与这两个数的差的积。动脑想一想(x+2)(x?2)(y+5)(y?5)a2-b2 =(a+b)(a-b)解:原式=(2x)2?32
=(2x+3)(2x?3)动脑想一想分解因式:4x2?94x2 = (2x)2
9=32a2?b2 =(a+b)(a?b)解:原式=[(x+p)+(x+q)][(x+p)–(x+q)]
=(2x+p+q)(p?q)动脑想一想分解因式:(x+p)2 – (x+q)2把(x+p)和 (x+q)各看成一个整体,分别看做公式中的a和b,再利用平方差公式解:原式=(x2+y2)(x2?y2)
=(x2+y2)(x+y)(x?y)
动脑想一想分解因式:x4-y4必须分解到每个多项式都不能再分解为止。(x2)2-(y2)2解:原式=ab(a2?1)
=ab(a+1)(a?1)动脑想一想分解因式:a3b – ab进一步用平方差公式进行分解。先提公因式观察下面的多项式,它们有什么特点?
x2?4x+4
y2+2x+1动脑想一想你还记得你在哪里见过类似这样的式子吗?x2?2·2x+22y2+2·1x+12a2±2ab+b2完全平方式形如下式的,带有两个同号平方项的二次三项式,叫做完全平方式:首平方,尾平方,首尾两倍在中央。a2±2ab+b2?动脑想一想是是不是不是是怎样把完全平方式因式分解呢?完全平方公式因式分解把完全平方公式等号两边互换,就得到:(a±b)2a2±2ab+b2两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方。动脑想一想(x?2)2(y+1)2a2±2ab+b =(a±b)2解:原式=(4x)2+2·4x·3+32
=(4x+3)2动脑想一想分解因式:16x2+24x+916x2=(4x)2
9=32
24x=2·4x·3a2±2ab+b =(a±b)2解:原式=?(x2?4xy+4y2)
=?[x2?2·x·2y+(2y)2]
=?(x?2y)2 动脑想一想分解因式: –x2+4xy–4y2先把首项的负号提出去,便于观察解:原式=3a(x2+2xy+y2)
=3a(x+y)2
动脑想一想分解因式:3ax2+6axy+3ay2有公因式3a,先提出来公因式,再进一步分解。解:原式=(a+b)2?2·(a+b)·6+62
=(a+b?6)2
动脑想一想分解因式:(a+b)2-12(a+b)+36把(a+b)看成一个整体,可看做完全平方式。小结:公式法分解因式把乘法公式的等号两端互换位置,就可以得到用来分解因式的公式,这就是公式法分解因式。a2±2ab+b =(a±b)2a2?b2 =(a+b)(a?b)学完本节课你应该知道公式法完全平方式完全平方公式把一个多项式化成几个整式的积因式分解平方差公式a2?b2 =(a+b)(a?b)a2±2ab+b2a2±2ab+b =(a±b)2动笔练一练下列式子中,可以用平方差公式因式分解的是 。
①x2+y2 ②x2-y2 ③-x2+y2 ④-x2-y2
下列式子中是完全平方式的是 。
①a2-4a+4 ②1+4a2 ③4b2+4b-1 ④a2+ab+b2② ③① ③动笔练一练(3a+2b)(3a?2b)y(x+2)(x-2)?(4+a2)(2+a)(2?a)动笔练一练?(x+y)2(2x?1)2a(a+x)2?3(x?y)2课后练一练请同学们独立完成配套课后练习题。下课!谢谢同学们!
