第四章机械能和能源第3_4节势能;动能动能定理3动能定理的简单应用同步练习
文档属性
| 名称 | 第四章机械能和能源第3_4节势能;动能动能定理3动能定理的简单应用同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 112.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-09-08 00:00:00 | ||
图片预览

文档简介
第3-4节 势能;动能 动能定理3 动能定理的简单应用
(答题时间:30分钟)
1. 一质量为30 kg的小孩从高度为2.0 m的滑梯顶端由静止开始滑下,滑到底端时的速度为2.0 m/s。取g=10 m/s2,关于力对小孩做的功,以下说法正确的是( )
A. 支持力做功50 J B. 阻力做功540 J
C. 合外力做功60 J D. 重力做功500 J
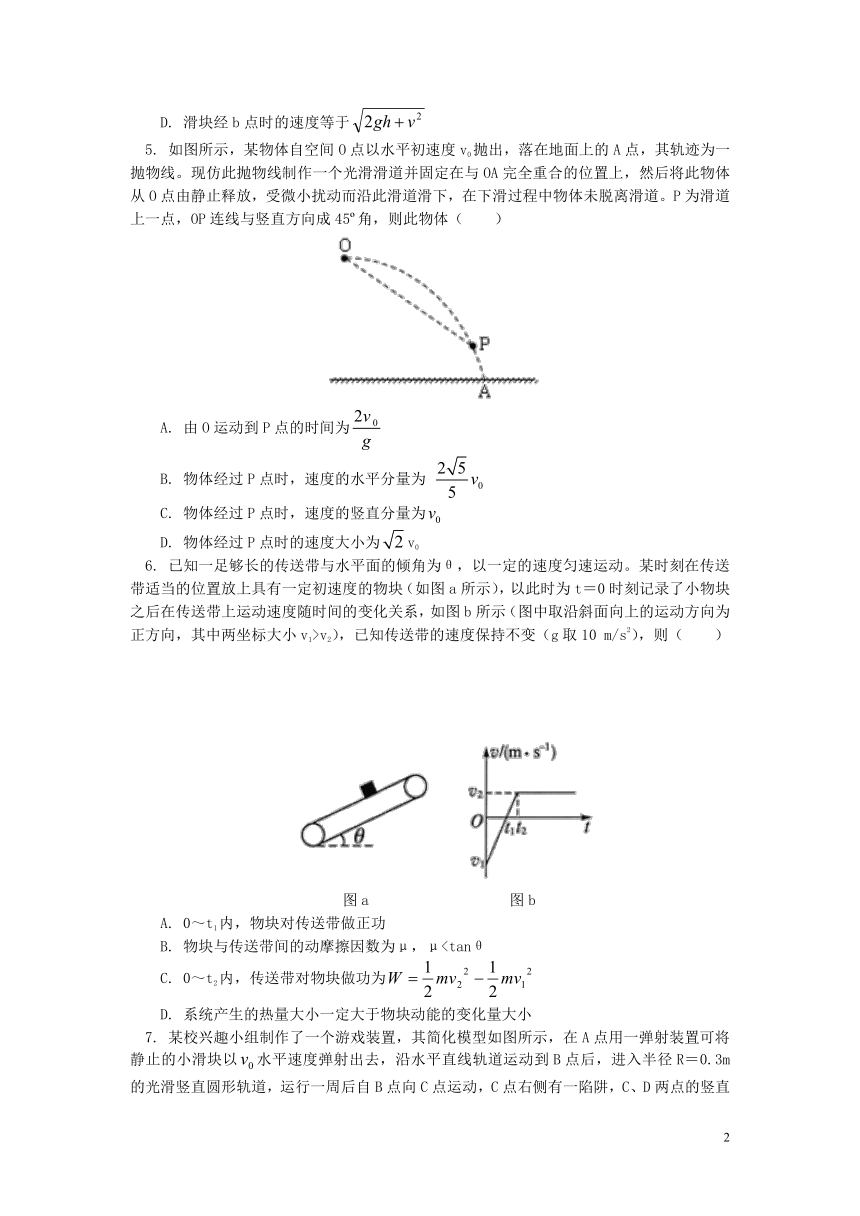
2. 如图所示,有一个足够长的斜坡,倾角为α=30o。一个小孩在做游戏时,从该斜坡顶端将一足球沿水平方向水平踢出去,已知足球被踢出时的初动能为9J,则该足球第一次落在斜坡上时的动能为( )
A. 12J B. 21J C. 27J D. 36J
3. 如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率v1匀速向右运动。一质量为m的滑块从传送带右端以水平向左的速率v2(v2 > v1)滑上传送带,最终滑块又返回至传送带的右端。就上述过程,下列判断正确的为( )
A. 滑块返回传送带右端的速率为v1
B. 此过程中传送带对滑块做功为
C. 此过程中电动机对传送带做功为2mv
D. 此过程中滑块与传送带间摩擦产生的热量为
4. 如图所示,质量为m的滑块从 h高处的a点沿圆弧轨道ab滑入水平轨道bc,滑块与轨道的动摩擦因数相同。滑块在a、c两点时的速度大小均为v,ab弧长与bc长度相等。空气阻力不计,则滑块从a到c的运动过程中( )
A. 滑块的动能始终保持不变
B. 滑块在bc过程克服阻力做的功一定等于mgh/2
C. 滑块经b点时的速度大于
D. 滑块经b点时的速度等于
5. 如图所示,某物体自空间O点以水平初速度v0抛出,落在地面上的A点,其轨迹为一抛物线。现仿此抛物线制作一个光滑滑道并固定在与OA完全重合的位置上,然后将此物体从O点由静止释放,受微小扰动而沿此滑道滑下,在下滑过程中物体未脱离滑道。P为滑道上一点,OP连线与竖直方向成45o角,则此物体( )
A. 由O运动到P点的时间为
B. 物体经过P点时,速度的水平分量为
C. 物体经过P点时,速度的竖直分量为
D. 物体经过P点时的速度大小为v0
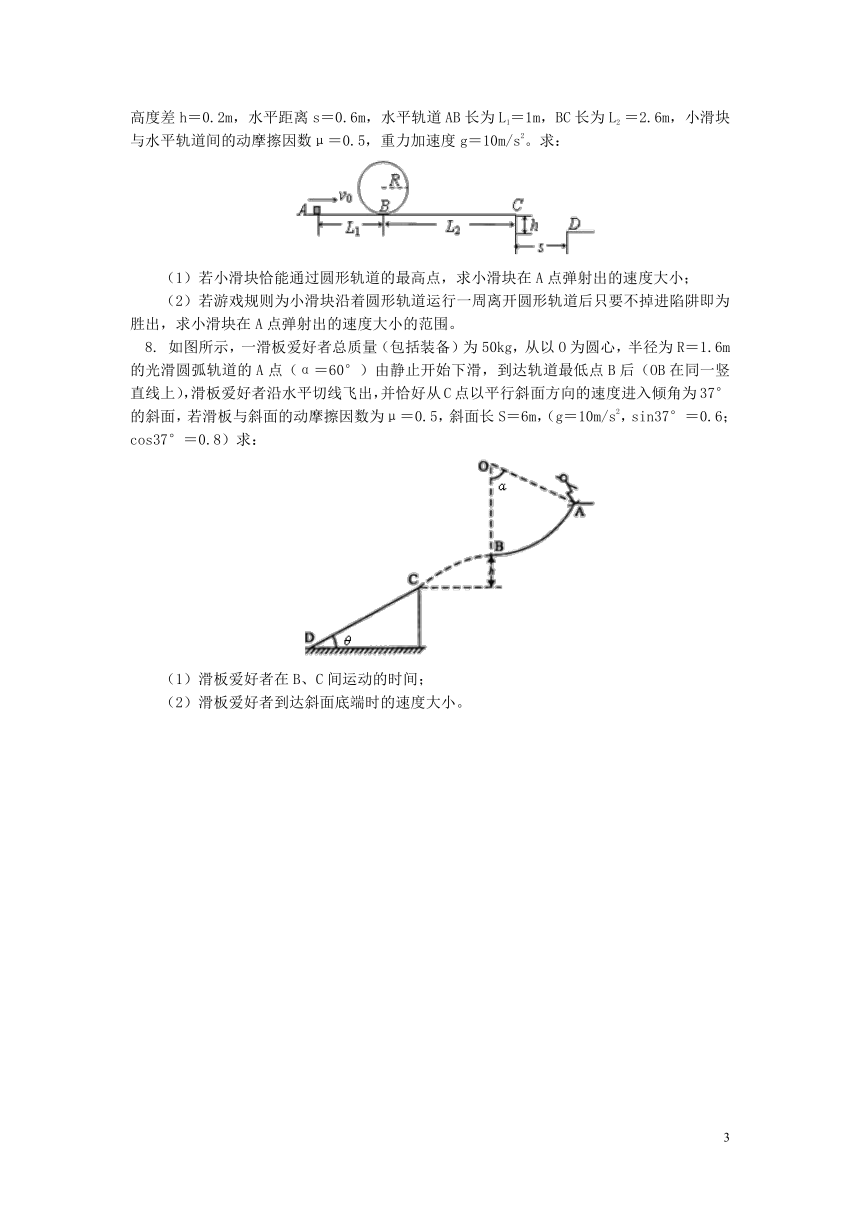
6. 已知一足够长的传送带与水平面的倾角为θ,以一定的速度匀速运动。某时刻在传送带适当的位置放上具有一定初速度的物块(如图a所示),以此时为t=0时刻记录了小物块之后在传送带上运动速度随时间的变化关系,如图b所示(图中取沿斜面向上的运动方向为正方向,其中两坐标大小v1>v2),已知传送带的速度保持不变(g取10 m/s2),则( )
图a 图b
A. 0~t1内,物块对传送带做正功
B. 物块与传送带间的动摩擦因数为μ,μC. 0~t2内,传送带对物块做功为
D. 系统产生的热量大小一定大于物块动能的变化量大小
7. 某校兴趣小组制作了一个游戏装置,其简化模型如图所示,在A点用一弹射装置可将静止的小滑块以水平速度弹射出去,沿水平直线轨道运动到B点后,进入半径R=0.3m的光滑竖直圆形轨道,运行一周后自B点向C点运动,C点右侧有一陷阱,C、D两点的竖直高度差h=0.2m,水平距离s=0.6m,水平轨道AB长为L1=1m,BC长为L2 =2.6m,小滑块与水平轨道间的动摩擦因数μ=0.5,重力加速度g=10m/s2。求:
(1)若小滑块恰能通过圆形轨道的最高点,求小滑块在A点弹射出的速度大小;
(2)若游戏规则为小滑块沿着圆形轨道运行一周离开圆形轨道后只要不掉进陷阱即为胜出,求小滑块在A点弹射出的速度大小的范围。
8. 如图所示,一滑板爱好者总质量(包括装备)为50kg,从以O为圆心,半径为R=1.6m的光滑圆弧轨道的A点(α=60°)由静止开始下滑,到达轨道最低点B后(OB在同一竖直线上),滑板爱好者沿水平切线飞出,并恰好从C点以平行斜面方向的速度进入倾角为37°的斜面,若滑板与斜面的动摩擦因数为μ=0.5,斜面长S=6m,(g=10m/s2,sin37°=0.6;cos37°=0.8)求:
(1)滑板爱好者在B、C间运动的时间;
(2)滑板爱好者到达斜面底端时的速度大小。
1. C 解析:因为滑梯对小孩的支持力与运动方向垂直,支持力不做功,故A错误;根据动能定理知,,故C正确;重力做功为 ,因为,则克服阻力做功,故B、D错误。
2. B 解析:足球做平抛运动,已知=mv02=9J,足球落地时的动能=m(v02+vy2),解得:=21J;故选B。
3. AD 解析:A. 由于传送带足够长,滑块减速向左滑行,直到速度减为零,然后滑块会在滑动摩擦力的作用下向右加速,由于v1<v2,滑块会先在滑动摩擦力的作用下加速,当速度增大到等于传送带速度时,滑块还在传送带上,之后不受摩擦力,故滑块与传送带一起向右匀速运动,有v′2=v1;故A正确;
B. 此过程中只有传送带对滑块做功,根据动能定理W′=△得:W′=△=,故B错误;
D. 设滑块向左运动的时间为t1,位移为x1,则:
摩擦力对滑块做功: ①
又摩擦力做功等于滑块动能的减小,即: ②
该过程中传送带的位移:x2=v1t1
摩擦力对滑块做功:W2=f·x2=f·v1t1= ③
将①②代入③得:W2=mv1v2
设滑块向左运动的时间为t2,位移为x3,则:
摩擦力对滑块做功:
该过程中传送带的位移:x4=v1t2=2x3
滑块相对传送带的总位移:x相=x1+x2+x4-x3=x1+x2+x3
滑动摩擦力对系统做功:
W总=f·x相=W1+W2+W3=
滑块与传送带间摩擦产生的热量大小等于通过滑动摩擦力对系统做功,Q=W总=f·=,故D正确;
C. 全过程中,电动机对传送带做的功与滑块动能的减小量等于滑块与传送带间摩擦产生的热量,即
整理得:,故C错误。
故选AD。
4. C 解析:滑块在a、c两点时的速度大小均为v,知滑块先加速后减速,动能先增加后减小,故A错误;对全程运用动能定理得,mgh-Wf=0,全程克服阻力做功等于mgh,因为ab段所受的支持力小于重力,所以所受的摩擦力与bc段不等,克服摩擦力做功不等,且在斜面上克服阻力做功小于在水平面克服阻力做功,则小球在bc过程克服阻力做的功不等于,故B错误;根据动能定理得:mgh-Wf′=,因为Wf′<,所以vb>,故C正确,D错误。故选C。
5. B 解析:竖直分位移与水平分位移大小相等,有v0t=gt2,,竖直方向上的分速度vy=gt=2v0。设瞬时速度方向与水平方向成θ角,则tanθ==2,从O到P做平抛运动的时间为,则沿轨道运动时,时间不为,故A错误;若从O点由静止释放,沿此滑道滑下,运动到P点,设OP竖直高度为h,根据动能定理得:mv2=mgh;而平抛运动时vy2=2gh;解得:v=2v0,故D错误;物体经过P点时,速度的水平分量为vx=vcosθ=2v0=,故B正确,C错误。故选B。
6. D 解析:分析题图b可知,传送带沿斜面向上运动;0~t1内,物块沿斜面向下运动,物块受到的摩擦力沿斜面向上,故传送带受到的摩擦力沿斜面向下,物块对传送带做负功,选项A错误;0~t1内,物块沿斜面向下减速运动,故物块加速度沿斜面向上,即μmgcosθ>mgsinθ,故μ>tanθ,选项B错误;0~t2内,传送带对物块做的功W加上物块重力做的功WG等于物块动能的增加量,即,根据v-t图象的“面积”法求位移可知,WG≠0,选项C错误;设0~t1内物块的位移大小为s1,t1~t2内物块的位移大小为s2,全过程物块与传送带之间有相对滑动,物块受到的摩擦力f大小恒定,系统的一部分机械能会通过“摩擦生热”转化为热量即内能,其大小Q=,对0~t1内和t1~t2内的物块运用动能定理,有-(f-mgsinθ)s1=0-mv,(f-mgsinθ)s2=mv,即f(s1+s2)=mv+mv+mgsinθ(s1+s2)>mv-mv,因>s1+s2,故Q=> f(s1+s2)>mv-mv,选项D正确。
7. 解:(1)小滑块恰能通过圆形轨道最高点的速度为v,由牛顿第二定律得:
①
从B到最高点小滑块机械能守恒有: ②
从A到B由动能定理得: ③
由①②③解得A点的速度为:。
(2)若小滑块刚好停在C处,从A到C由动能定理得:
解得A点的速度为
若小滑块停在BC段,应满足5m/s≤vA≤6m/s
若小滑块能通过C点并恰好越过陷阱,利用平抛运动则有:
竖直方向:
水平方向:
从A到C由动能定理得:
解得:
所以初速度的范围为:5m/s≤vA≤6m/s和vA≥。
8. 解:(1)滑板爱好者在圆形轨道AB间运动的过程中,机械能守恒
解得:vB=4m/s
滑板爱好者在BC之间做平抛运动,在C点:竖直方向的分速度:
由vcy=gt,解得平抛运动的时间:t=0.3s。
(2)在C点,由平抛运动的规律可知:
滑板爱好者在斜面上运动的过程中,由动能定理可得:
解得:vD=7m/s。
(答题时间:30分钟)
1. 一质量为30 kg的小孩从高度为2.0 m的滑梯顶端由静止开始滑下,滑到底端时的速度为2.0 m/s。取g=10 m/s2,关于力对小孩做的功,以下说法正确的是( )
A. 支持力做功50 J B. 阻力做功540 J
C. 合外力做功60 J D. 重力做功500 J
2. 如图所示,有一个足够长的斜坡,倾角为α=30o。一个小孩在做游戏时,从该斜坡顶端将一足球沿水平方向水平踢出去,已知足球被踢出时的初动能为9J,则该足球第一次落在斜坡上时的动能为( )
A. 12J B. 21J C. 27J D. 36J
3. 如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率v1匀速向右运动。一质量为m的滑块从传送带右端以水平向左的速率v2(v2 > v1)滑上传送带,最终滑块又返回至传送带的右端。就上述过程,下列判断正确的为( )
A. 滑块返回传送带右端的速率为v1
B. 此过程中传送带对滑块做功为
C. 此过程中电动机对传送带做功为2mv
D. 此过程中滑块与传送带间摩擦产生的热量为
4. 如图所示,质量为m的滑块从 h高处的a点沿圆弧轨道ab滑入水平轨道bc,滑块与轨道的动摩擦因数相同。滑块在a、c两点时的速度大小均为v,ab弧长与bc长度相等。空气阻力不计,则滑块从a到c的运动过程中( )
A. 滑块的动能始终保持不变
B. 滑块在bc过程克服阻力做的功一定等于mgh/2
C. 滑块经b点时的速度大于
D. 滑块经b点时的速度等于
5. 如图所示,某物体自空间O点以水平初速度v0抛出,落在地面上的A点,其轨迹为一抛物线。现仿此抛物线制作一个光滑滑道并固定在与OA完全重合的位置上,然后将此物体从O点由静止释放,受微小扰动而沿此滑道滑下,在下滑过程中物体未脱离滑道。P为滑道上一点,OP连线与竖直方向成45o角,则此物体( )
A. 由O运动到P点的时间为
B. 物体经过P点时,速度的水平分量为
C. 物体经过P点时,速度的竖直分量为
D. 物体经过P点时的速度大小为v0
6. 已知一足够长的传送带与水平面的倾角为θ,以一定的速度匀速运动。某时刻在传送带适当的位置放上具有一定初速度的物块(如图a所示),以此时为t=0时刻记录了小物块之后在传送带上运动速度随时间的变化关系,如图b所示(图中取沿斜面向上的运动方向为正方向,其中两坐标大小v1>v2),已知传送带的速度保持不变(g取10 m/s2),则( )
图a 图b
A. 0~t1内,物块对传送带做正功
B. 物块与传送带间的动摩擦因数为μ,μ
D. 系统产生的热量大小一定大于物块动能的变化量大小
7. 某校兴趣小组制作了一个游戏装置,其简化模型如图所示,在A点用一弹射装置可将静止的小滑块以水平速度弹射出去,沿水平直线轨道运动到B点后,进入半径R=0.3m的光滑竖直圆形轨道,运行一周后自B点向C点运动,C点右侧有一陷阱,C、D两点的竖直高度差h=0.2m,水平距离s=0.6m,水平轨道AB长为L1=1m,BC长为L2 =2.6m,小滑块与水平轨道间的动摩擦因数μ=0.5,重力加速度g=10m/s2。求:
(1)若小滑块恰能通过圆形轨道的最高点,求小滑块在A点弹射出的速度大小;
(2)若游戏规则为小滑块沿着圆形轨道运行一周离开圆形轨道后只要不掉进陷阱即为胜出,求小滑块在A点弹射出的速度大小的范围。
8. 如图所示,一滑板爱好者总质量(包括装备)为50kg,从以O为圆心,半径为R=1.6m的光滑圆弧轨道的A点(α=60°)由静止开始下滑,到达轨道最低点B后(OB在同一竖直线上),滑板爱好者沿水平切线飞出,并恰好从C点以平行斜面方向的速度进入倾角为37°的斜面,若滑板与斜面的动摩擦因数为μ=0.5,斜面长S=6m,(g=10m/s2,sin37°=0.6;cos37°=0.8)求:
(1)滑板爱好者在B、C间运动的时间;
(2)滑板爱好者到达斜面底端时的速度大小。
1. C 解析:因为滑梯对小孩的支持力与运动方向垂直,支持力不做功,故A错误;根据动能定理知,,故C正确;重力做功为 ,因为,则克服阻力做功,故B、D错误。
2. B 解析:足球做平抛运动,已知=mv02=9J,足球落地时的动能=m(v02+vy2),解得:=21J;故选B。
3. AD 解析:A. 由于传送带足够长,滑块减速向左滑行,直到速度减为零,然后滑块会在滑动摩擦力的作用下向右加速,由于v1<v2,滑块会先在滑动摩擦力的作用下加速,当速度增大到等于传送带速度时,滑块还在传送带上,之后不受摩擦力,故滑块与传送带一起向右匀速运动,有v′2=v1;故A正确;
B. 此过程中只有传送带对滑块做功,根据动能定理W′=△得:W′=△=,故B错误;
D. 设滑块向左运动的时间为t1,位移为x1,则:
摩擦力对滑块做功: ①
又摩擦力做功等于滑块动能的减小,即: ②
该过程中传送带的位移:x2=v1t1
摩擦力对滑块做功:W2=f·x2=f·v1t1= ③
将①②代入③得:W2=mv1v2
设滑块向左运动的时间为t2,位移为x3,则:
摩擦力对滑块做功:
该过程中传送带的位移:x4=v1t2=2x3
滑块相对传送带的总位移:x相=x1+x2+x4-x3=x1+x2+x3
滑动摩擦力对系统做功:
W总=f·x相=W1+W2+W3=
滑块与传送带间摩擦产生的热量大小等于通过滑动摩擦力对系统做功,Q=W总=f·=,故D正确;
C. 全过程中,电动机对传送带做的功与滑块动能的减小量等于滑块与传送带间摩擦产生的热量,即
整理得:,故C错误。
故选AD。
4. C 解析:滑块在a、c两点时的速度大小均为v,知滑块先加速后减速,动能先增加后减小,故A错误;对全程运用动能定理得,mgh-Wf=0,全程克服阻力做功等于mgh,因为ab段所受的支持力小于重力,所以所受的摩擦力与bc段不等,克服摩擦力做功不等,且在斜面上克服阻力做功小于在水平面克服阻力做功,则小球在bc过程克服阻力做的功不等于,故B错误;根据动能定理得:mgh-Wf′=,因为Wf′<,所以vb>,故C正确,D错误。故选C。
5. B 解析:竖直分位移与水平分位移大小相等,有v0t=gt2,,竖直方向上的分速度vy=gt=2v0。设瞬时速度方向与水平方向成θ角,则tanθ==2,从O到P做平抛运动的时间为,则沿轨道运动时,时间不为,故A错误;若从O点由静止释放,沿此滑道滑下,运动到P点,设OP竖直高度为h,根据动能定理得:mv2=mgh;而平抛运动时vy2=2gh;解得:v=2v0,故D错误;物体经过P点时,速度的水平分量为vx=vcosθ=2v0=,故B正确,C错误。故选B。
6. D 解析:分析题图b可知,传送带沿斜面向上运动;0~t1内,物块沿斜面向下运动,物块受到的摩擦力沿斜面向上,故传送带受到的摩擦力沿斜面向下,物块对传送带做负功,选项A错误;0~t1内,物块沿斜面向下减速运动,故物块加速度沿斜面向上,即μmgcosθ>mgsinθ,故μ>tanθ,选项B错误;0~t2内,传送带对物块做的功W加上物块重力做的功WG等于物块动能的增加量,即,根据v-t图象的“面积”法求位移可知,WG≠0,选项C错误;设0~t1内物块的位移大小为s1,t1~t2内物块的位移大小为s2,全过程物块与传送带之间有相对滑动,物块受到的摩擦力f大小恒定,系统的一部分机械能会通过“摩擦生热”转化为热量即内能,其大小Q=,对0~t1内和t1~t2内的物块运用动能定理,有-(f-mgsinθ)s1=0-mv,(f-mgsinθ)s2=mv,即f(s1+s2)=mv+mv+mgsinθ(s1+s2)>mv-mv,因>s1+s2,故Q=> f(s1+s2)>mv-mv,选项D正确。
7. 解:(1)小滑块恰能通过圆形轨道最高点的速度为v,由牛顿第二定律得:
①
从B到最高点小滑块机械能守恒有: ②
从A到B由动能定理得: ③
由①②③解得A点的速度为:。
(2)若小滑块刚好停在C处,从A到C由动能定理得:
解得A点的速度为
若小滑块停在BC段,应满足5m/s≤vA≤6m/s
若小滑块能通过C点并恰好越过陷阱,利用平抛运动则有:
竖直方向:
水平方向:
从A到C由动能定理得:
解得:
所以初速度的范围为:5m/s≤vA≤6m/s和vA≥。
8. 解:(1)滑板爱好者在圆形轨道AB间运动的过程中,机械能守恒
解得:vB=4m/s
滑板爱好者在BC之间做平抛运动,在C点:竖直方向的分速度:
由vcy=gt,解得平抛运动的时间:t=0.3s。
(2)在C点,由平抛运动的规律可知:
滑板爱好者在斜面上运动的过程中,由动能定理可得:
解得:vD=7m/s。
