第四章机械能和能源第3_4节势能;动能动能定理6利用动能定理分析多过程问题同步练习
文档属性
| 名称 | 第四章机械能和能源第3_4节势能;动能动能定理6利用动能定理分析多过程问题同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 120.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-09-08 10:59:34 | ||
图片预览

文档简介
第3-4节 势能;动能 动能定理6 利用动能定理分析多过程问题
(答题时间:30分钟)
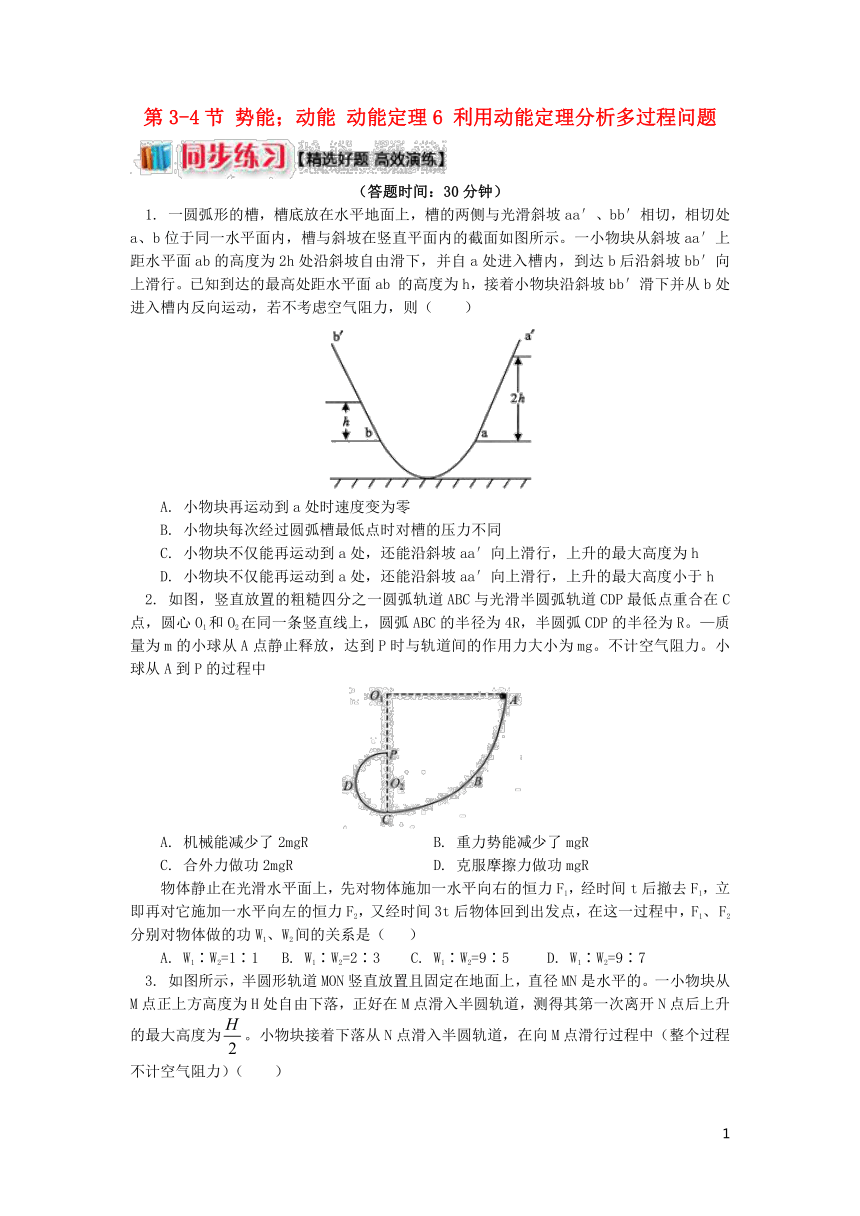
1. 一圆弧形的槽,槽底放在水平地面上,槽的两侧与光滑斜坡aa′、bb′相切,相切处a、b位于同一水平面内,槽与斜坡在竖直平面内的截面如图所示。一小物块从斜坡aa′上距水平面ab的高度为2h处沿斜坡自由滑下,并自a处进入槽内,到达b后沿斜坡bb′向上滑行。已知到达的最高处距水平面ab 的高度为h,接着小物块沿斜坡bb′滑下并从b处进入槽内反向运动,若不考虑空气阻力,则( )
A. 小物块再运动到a处时速度变为零
B. 小物块每次经过圆弧槽最低点时对槽的压力不同
C. 小物块不仅能再运动到a处,还能沿斜坡aa′向上滑行,上升的最大高度为h
D. 小物块不仅能再运动到a处,还能沿斜坡aa′向上滑行,上升的最大高度小于h
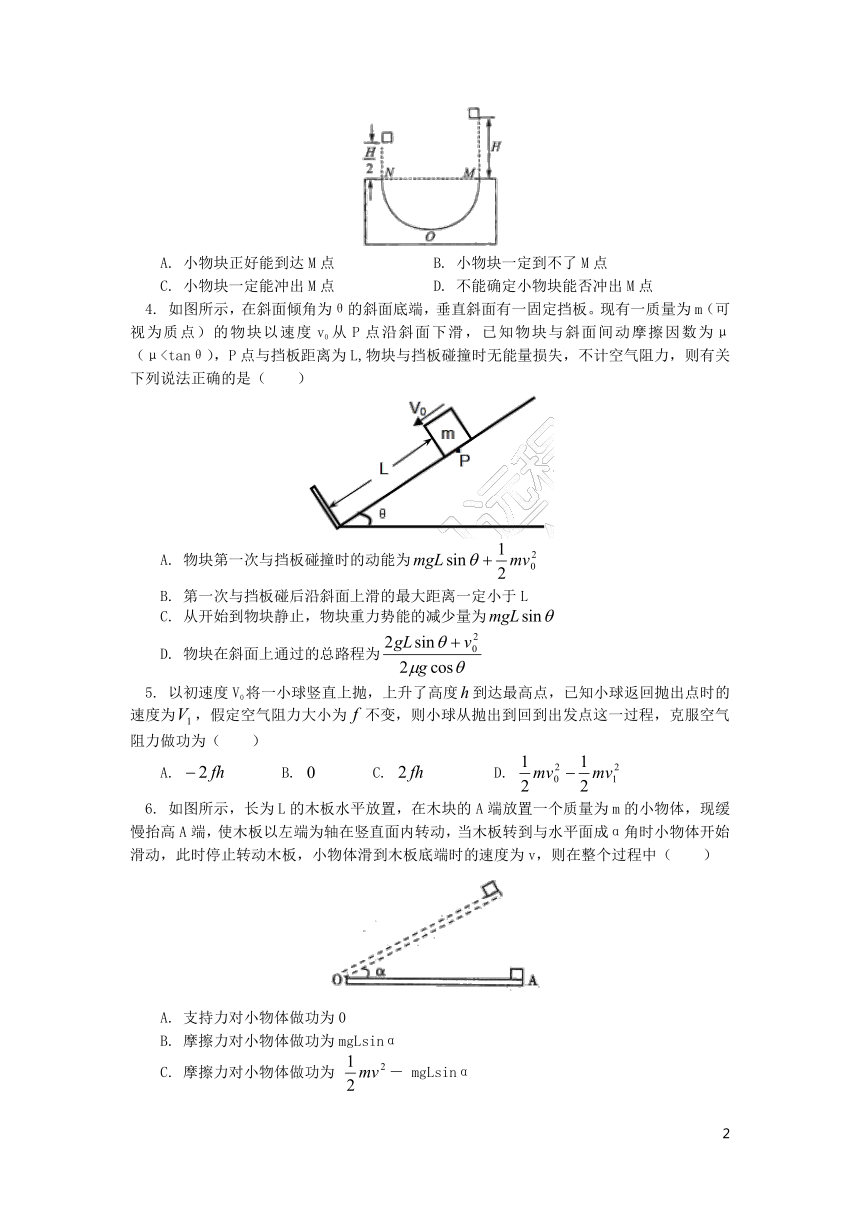
2. 如图,竖直放置的粗糙四分之一圆弧轨道ABC与光滑半圆弧轨道CDP最低点重合在C 点,圆心O1和O2在同一条竖直线上,圆弧ABC的半径为4R,半圆弧CDP的半径为R。—质量为m的小球从A点静止释放,达到P时与轨道间的作用力大小为mg。不计空气阻力。小球从A到P的过程中
A. 机械能减少了2mgR B. 重力势能减少了mgR
C. 合外力做功2mgR D. 克服摩擦力做功mgR
物体静止在光滑水平面上,先对物体施加一水平向右的恒力F1,经时间t后撤去F1,立即再对它施加一水平向左的恒力F2,又经时间3t后物体回到出发点,在这一过程中,F1、 F2分别对物体做的功W1、W2间的关系是( )
A. W1∶W2=1∶1 B. W1∶W2=2∶3 C. W1∶W2=9∶5 D. W1∶W2=9∶7
3. 如图所示,半圆形轨道MON竖直放置且固定在地面上,直径MN是水平的。一小物块从M点正上方高度为H处自由下落,正好在M点滑入半圆轨道,测得其第一次离开N点后上升的最大高度为。小物块接着下落从N点滑入半圆轨道,在向M点滑行过程中(整个过程不计空气阻力)( )
A. 小物块正好能到达M点 B. 小物块一定到不了M点
C. 小物块一定能冲出M点 D. 不能确定小物块能否冲出M点
4. 如图所示,在斜面倾角为θ的斜面底端,垂直斜面有一固定挡板。现有一质量为m(可视为质点)的物块以速度v0从P点沿斜面下滑,已知物块与斜面间动摩擦因数为μ(μA. 物块第一次与挡板碰撞时的动能为
B. 第一次与挡板碰后沿斜面上滑的最大距离一定小于L
C. 从开始到物块静止,物块重力势能的减少量为
D. 物块在斜面上通过的总路程为
5. 以初速度V0将一小球竖直上抛,上升了高度到达最高点,已知小球返回抛出点时的速度为,假定空气阻力大小为不变,则小球从抛出到回到出发点这一过程,克服空气阻力做功为( )
A. B. C. D.
6. 如图所示,长为L的木板水平放置,在木块的A端放置一个质量为m的小物体,现缓慢抬高A端,使木板以左端为轴在竖直面内转动,当木板转到与水平面成α角时小物体开始滑动,此时停止转动木板,小物体滑到木板底端时的速度为v,则在整个过程中( )
A. 支持力对小物体做功为0
B. 摩擦力对小物体做功为mgLsinα
C. 摩擦力对小物体做功为 - mgLsinα
D. 木板对小物体做功为
7. 如图所示,半径R=0.5m的光滑圆弧面CDM分别与光滑斜面体ABC和斜面MN相切于C、M点,斜面倾角分别如图所示。O为圆弧圆心,D为圆弧最低点,C、M在同一水平高度。斜面体ABC固定在地面上,顶端B安装一定滑轮,一轻质软细绳跨过定滑轮(不计滑轮摩擦)分别连接小物块P、Q (两边细绳分别与对应斜面平行),并保持P、Q两物块静止。若PC间距为L1=0.25m,斜面MN足够长,物块P质量m1= 3kg,与MN间的动摩擦因数,重力加速度g=10m/s2。(sin37°=0.6,cos37°=0.8)求:
(1)小物块Q的质量m2;
(2)烧断细绳后,物块P第一次到达D点时对轨道的压力大小;
(3)物块P在MN斜面上滑行的总路程。
1. BD 解析:因要克服摩擦阻力做功,所以每次通过最低点的速度会变小,根据圆周运动公式及牛顿第二定律有,故可知物块与圆弧槽间的正压力会变小,所以B正确;设第一次通过圆弧槽过程中克服摩擦力做功为,根据动能定理可得,第二次通过圆弧槽的最低点时因正压力减小,所以摩擦力减小;同理,其他位置所对应的摩擦力都变小,故第二次通过圆弧槽克服摩擦力做的功将小于第一次,即,所以D正确,A、C错误。
2. D 解析:令恒力F1作用时间t后物体的速度为v1,恒力F2又作用时间3t后物体的速度为v2,所以物体在恒力F1作用时间t后物体的位移为,物体在恒力F2作用下的位移,由题意知,整理得:,由动能定理得:,,代入解得,故选项D正确。
3. C 解析:第一次飞出过程根据动能定理得mg-Wf=0,再次到达M点过程中,根据动能定理mg-=,因第二次经过半圆轨道过程中物块对轨道的压力减少,故摩擦力减小,克服阻力做功<Wf,故速度v>0,故能冲出M点,故选项C正确,其余都错误。
4. CD 解析:根据动能定理,在下落到挡板前设碰撞前速度为,利用动能定理有,所以A错。假设物体初速度为0,则第一次与挡板碰后沿斜面上滑的最大距离一定小于L,但由于有初速度,初速度对应的动能可能大于摩擦力消耗的能量,因此B错。从开始到物块静止,物块重力势能的减少量为,正确。利用动能定理,则物块在斜面上通过的总路程为s,即
,化简则。故选C、D。
5. CD 解析:上升、下降阻力做功大小都为W=-fh,所以克服阻力做功为2fh,根据动能定理,即克服阻力做功为,因此答案为C、D。
6. CD 解析:物块在缓慢提高过程中,静摩擦力始终与运动方向垂直,所以摩擦力不做功,物块在滑动过程中,由动能定理可得:,则有滑动摩擦力做功为,所以克服摩擦力做功为,所以B错误,C正确;在下滑的过程中,支持力不做功,在上升的过程中,根据动能定理可得,,所以支持力对物体做功为,所以A错误;木板对物体做功为支持力和摩擦力对物体做功的和,所以木板对物体做功为,所以D正确,故选C、D。
7. 解:(1)根据平衡,满足:
可得;
(2)P到D过程由动能定理得
由几何关系
运动到D点时,根据牛顿第二定律:
解得
由牛顿第三定律得,物块P对轨道的压力大小为78N;
(3)分析可知最终物块在CDM之间往复运动,C点和M点速度为零。
由全过程动能定理得:
解得
(答题时间:30分钟)
1. 一圆弧形的槽,槽底放在水平地面上,槽的两侧与光滑斜坡aa′、bb′相切,相切处a、b位于同一水平面内,槽与斜坡在竖直平面内的截面如图所示。一小物块从斜坡aa′上距水平面ab的高度为2h处沿斜坡自由滑下,并自a处进入槽内,到达b后沿斜坡bb′向上滑行。已知到达的最高处距水平面ab 的高度为h,接着小物块沿斜坡bb′滑下并从b处进入槽内反向运动,若不考虑空气阻力,则( )
A. 小物块再运动到a处时速度变为零
B. 小物块每次经过圆弧槽最低点时对槽的压力不同
C. 小物块不仅能再运动到a处,还能沿斜坡aa′向上滑行,上升的最大高度为h
D. 小物块不仅能再运动到a处,还能沿斜坡aa′向上滑行,上升的最大高度小于h
2. 如图,竖直放置的粗糙四分之一圆弧轨道ABC与光滑半圆弧轨道CDP最低点重合在C 点,圆心O1和O2在同一条竖直线上,圆弧ABC的半径为4R,半圆弧CDP的半径为R。—质量为m的小球从A点静止释放,达到P时与轨道间的作用力大小为mg。不计空气阻力。小球从A到P的过程中
A. 机械能减少了2mgR B. 重力势能减少了mgR
C. 合外力做功2mgR D. 克服摩擦力做功mgR
物体静止在光滑水平面上,先对物体施加一水平向右的恒力F1,经时间t后撤去F1,立即再对它施加一水平向左的恒力F2,又经时间3t后物体回到出发点,在这一过程中,F1、 F2分别对物体做的功W1、W2间的关系是( )
A. W1∶W2=1∶1 B. W1∶W2=2∶3 C. W1∶W2=9∶5 D. W1∶W2=9∶7
3. 如图所示,半圆形轨道MON竖直放置且固定在地面上,直径MN是水平的。一小物块从M点正上方高度为H处自由下落,正好在M点滑入半圆轨道,测得其第一次离开N点后上升的最大高度为。小物块接着下落从N点滑入半圆轨道,在向M点滑行过程中(整个过程不计空气阻力)( )
A. 小物块正好能到达M点 B. 小物块一定到不了M点
C. 小物块一定能冲出M点 D. 不能确定小物块能否冲出M点
4. 如图所示,在斜面倾角为θ的斜面底端,垂直斜面有一固定挡板。现有一质量为m(可视为质点)的物块以速度v0从P点沿斜面下滑,已知物块与斜面间动摩擦因数为μ(μ
B. 第一次与挡板碰后沿斜面上滑的最大距离一定小于L
C. 从开始到物块静止,物块重力势能的减少量为
D. 物块在斜面上通过的总路程为
5. 以初速度V0将一小球竖直上抛,上升了高度到达最高点,已知小球返回抛出点时的速度为,假定空气阻力大小为不变,则小球从抛出到回到出发点这一过程,克服空气阻力做功为( )
A. B. C. D.
6. 如图所示,长为L的木板水平放置,在木块的A端放置一个质量为m的小物体,现缓慢抬高A端,使木板以左端为轴在竖直面内转动,当木板转到与水平面成α角时小物体开始滑动,此时停止转动木板,小物体滑到木板底端时的速度为v,则在整个过程中( )
A. 支持力对小物体做功为0
B. 摩擦力对小物体做功为mgLsinα
C. 摩擦力对小物体做功为 - mgLsinα
D. 木板对小物体做功为
7. 如图所示,半径R=0.5m的光滑圆弧面CDM分别与光滑斜面体ABC和斜面MN相切于C、M点,斜面倾角分别如图所示。O为圆弧圆心,D为圆弧最低点,C、M在同一水平高度。斜面体ABC固定在地面上,顶端B安装一定滑轮,一轻质软细绳跨过定滑轮(不计滑轮摩擦)分别连接小物块P、Q (两边细绳分别与对应斜面平行),并保持P、Q两物块静止。若PC间距为L1=0.25m,斜面MN足够长,物块P质量m1= 3kg,与MN间的动摩擦因数,重力加速度g=10m/s2。(sin37°=0.6,cos37°=0.8)求:
(1)小物块Q的质量m2;
(2)烧断细绳后,物块P第一次到达D点时对轨道的压力大小;
(3)物块P在MN斜面上滑行的总路程。
1. BD 解析:因要克服摩擦阻力做功,所以每次通过最低点的速度会变小,根据圆周运动公式及牛顿第二定律有,故可知物块与圆弧槽间的正压力会变小,所以B正确;设第一次通过圆弧槽过程中克服摩擦力做功为,根据动能定理可得,第二次通过圆弧槽的最低点时因正压力减小,所以摩擦力减小;同理,其他位置所对应的摩擦力都变小,故第二次通过圆弧槽克服摩擦力做的功将小于第一次,即,所以D正确,A、C错误。
2. D 解析:令恒力F1作用时间t后物体的速度为v1,恒力F2又作用时间3t后物体的速度为v2,所以物体在恒力F1作用时间t后物体的位移为,物体在恒力F2作用下的位移,由题意知,整理得:,由动能定理得:,,代入解得,故选项D正确。
3. C 解析:第一次飞出过程根据动能定理得mg-Wf=0,再次到达M点过程中,根据动能定理mg-=,因第二次经过半圆轨道过程中物块对轨道的压力减少,故摩擦力减小,克服阻力做功<Wf,故速度v>0,故能冲出M点,故选项C正确,其余都错误。
4. CD 解析:根据动能定理,在下落到挡板前设碰撞前速度为,利用动能定理有,所以A错。假设物体初速度为0,则第一次与挡板碰后沿斜面上滑的最大距离一定小于L,但由于有初速度,初速度对应的动能可能大于摩擦力消耗的能量,因此B错。从开始到物块静止,物块重力势能的减少量为,正确。利用动能定理,则物块在斜面上通过的总路程为s,即
,化简则。故选C、D。
5. CD 解析:上升、下降阻力做功大小都为W=-fh,所以克服阻力做功为2fh,根据动能定理,即克服阻力做功为,因此答案为C、D。
6. CD 解析:物块在缓慢提高过程中,静摩擦力始终与运动方向垂直,所以摩擦力不做功,物块在滑动过程中,由动能定理可得:,则有滑动摩擦力做功为,所以克服摩擦力做功为,所以B错误,C正确;在下滑的过程中,支持力不做功,在上升的过程中,根据动能定理可得,,所以支持力对物体做功为,所以A错误;木板对物体做功为支持力和摩擦力对物体做功的和,所以木板对物体做功为,所以D正确,故选C、D。
7. 解:(1)根据平衡,满足:
可得;
(2)P到D过程由动能定理得
由几何关系
运动到D点时,根据牛顿第二定律:
解得
由牛顿第三定律得,物块P对轨道的压力大小为78N;
(3)分析可知最终物块在CDM之间往复运动,C点和M点速度为零。
由全过程动能定理得:
解得
