12.3角的平分线的性质课件(第一课时,共33张PPT)
文档属性
| 名称 | 12.3角的平分线的性质课件(第一课时,共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 925.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-08 00:00:00 | ||
图片预览



文档简介
课件33张PPT。第十二章 全等三角形12.3 角的平分线的性质
会用尺规作图画定角的角平分线,并能用全等三角形的判定解释其原理。
掌握角平分线的性质,会运用性质解决相关问题,并能证明这一命题。
掌握角平分线的判定定理,理解角平分线的判定定理和性质定理的关系。现在有一张用纸做的角,怎样不利用其他工具把它平分?
对折之后的折痕和这个角有什么关系?
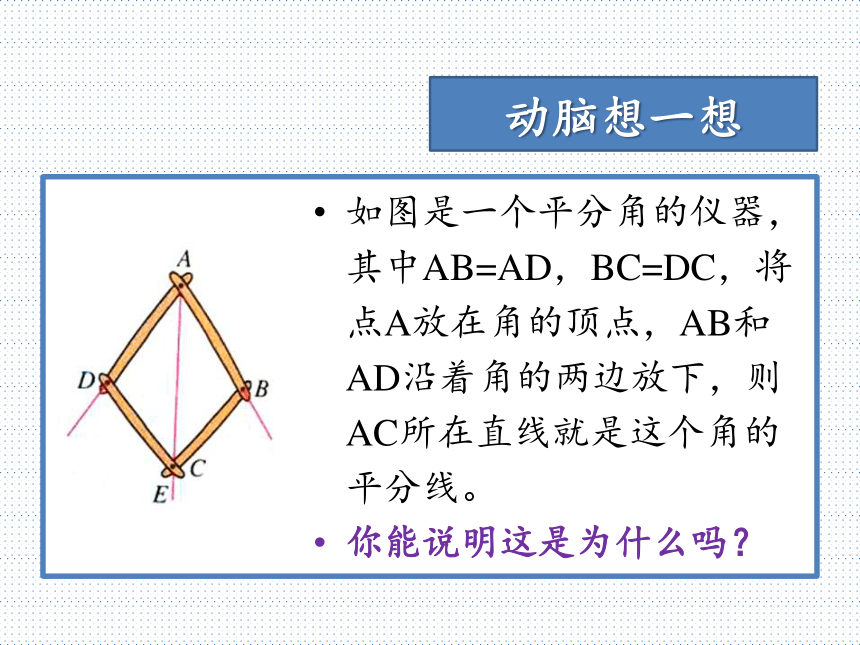
如果是木板不能对折,该怎么平分?动脑想一想如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,则AC所在直线就是这个角的平分线。
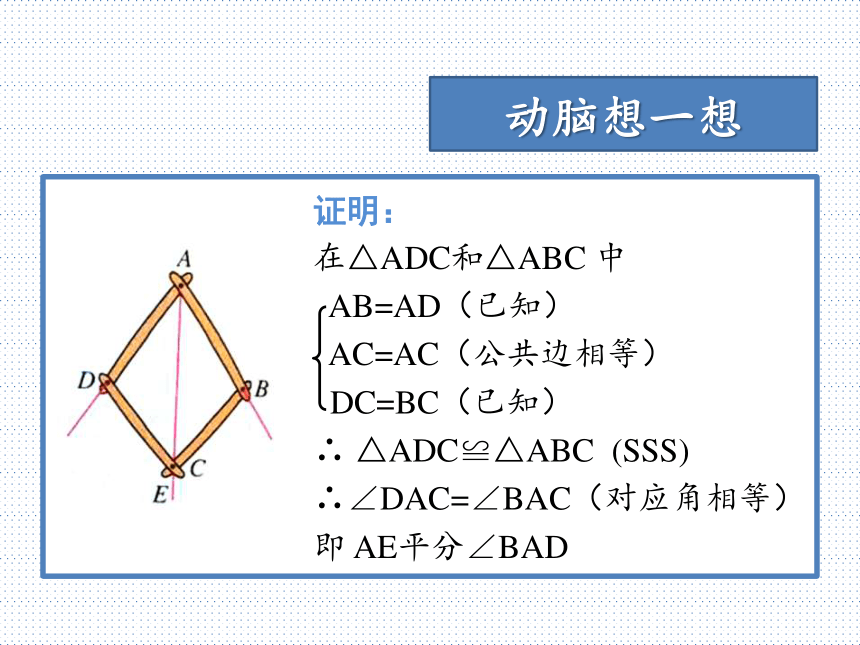
你能说明这是为什么吗?动脑想一想证明:
在△ADC和△ABC 中
AB=AD(已知)
AC=AC(公共边相等)
DC=BC(已知)
∴ △ADC≌△ABC (SSS)
∴∠DAC=∠BAC(对应角相等)
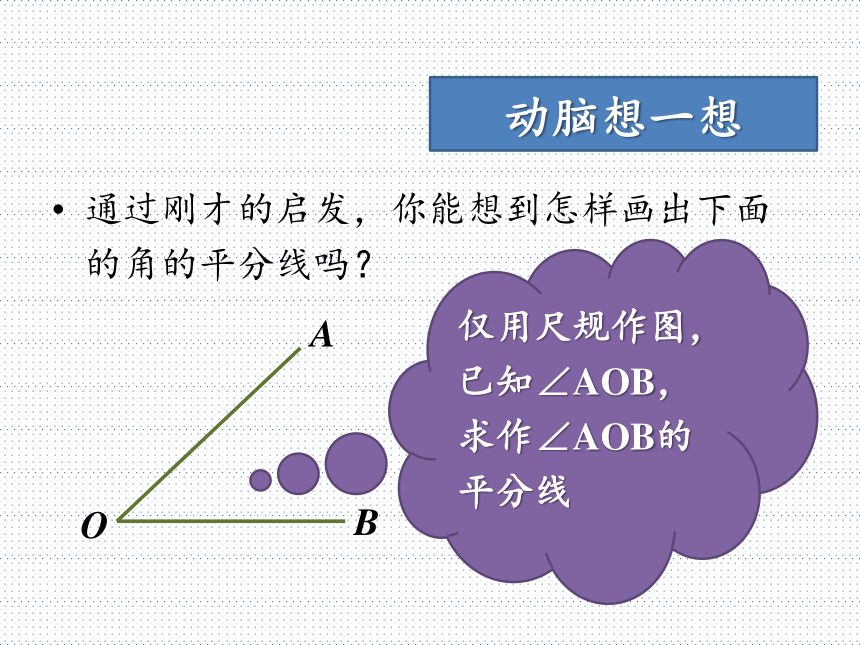
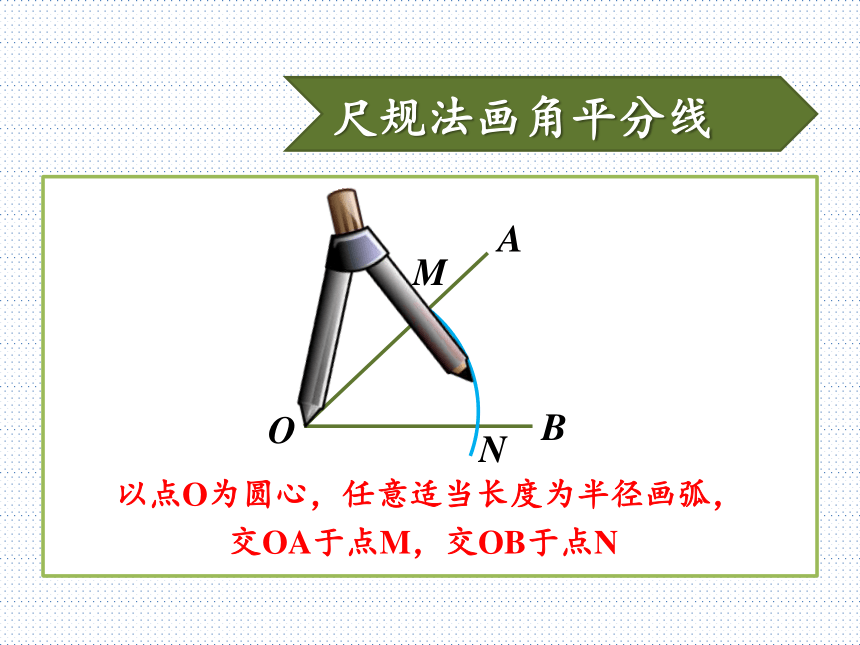
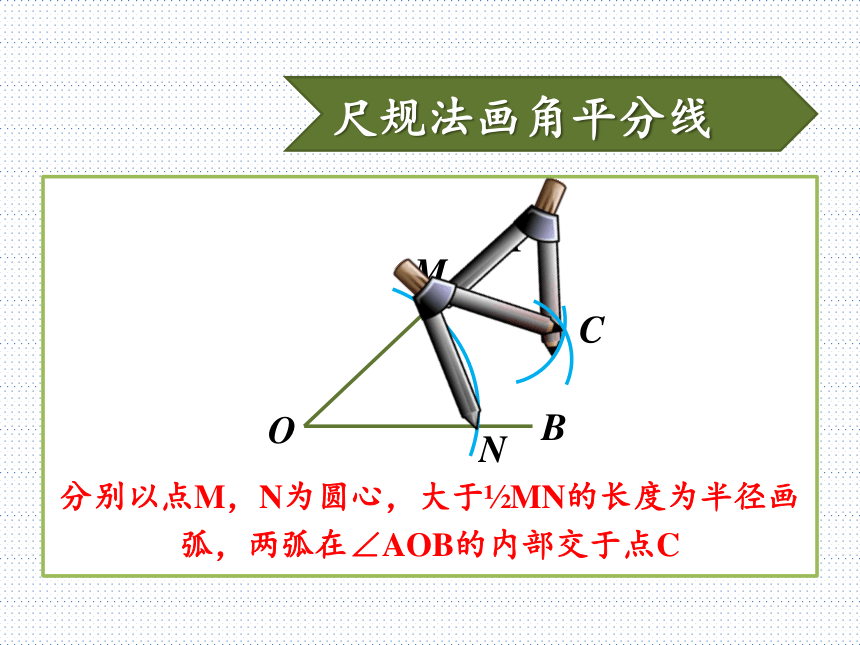
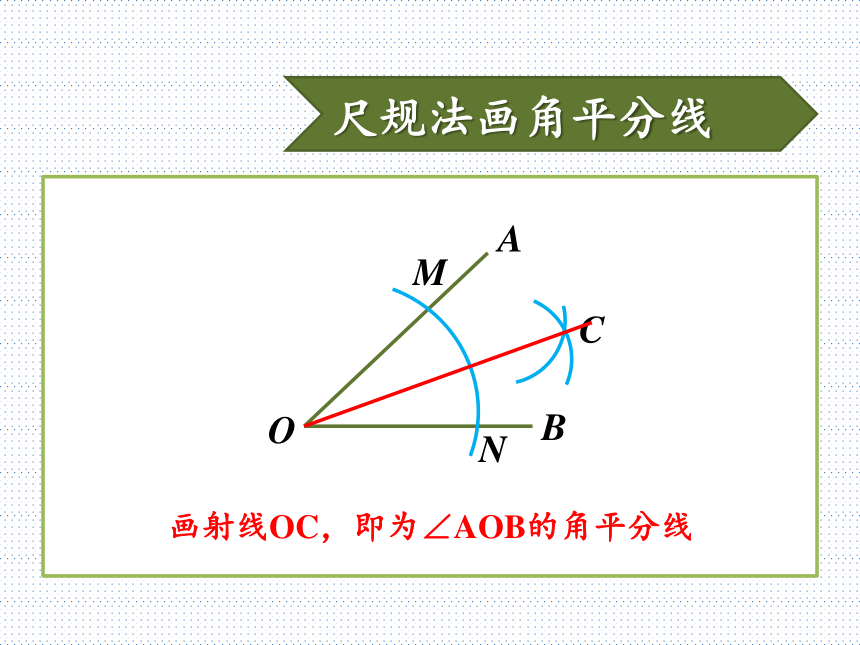
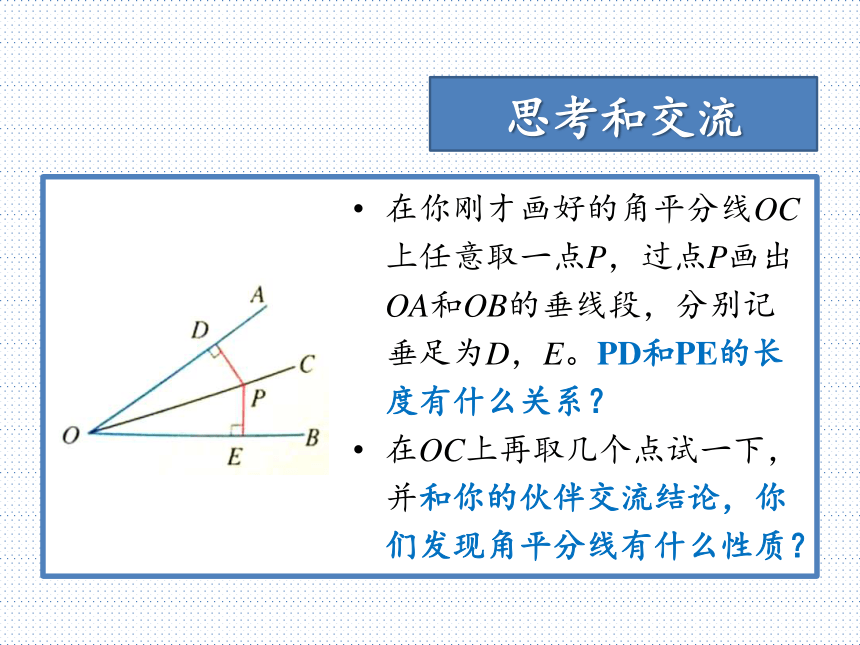
即 AE平分∠BAD动脑想一想通过刚才的启发,你能想到怎样画出下面的角的平分线吗?动脑想一想BAO仅用尺规作图,已知∠AOB,求作∠AOB的平分线尺规法画角平分线BAO以点O为圆心,任意适当长度为半径画弧,交OA于点M,交OB于点NMN尺规法画角平分线BAO分别以点M,N为圆心,大于?MN的长度为半径画弧,两弧在∠AOB的内部交于点CMNC尺规法画角平分线BAO画射线OC,即为∠AOB的角平分线MNC思考和交流在你刚才画好的角平分线OC上任意取一点P,过点P画出OA和OB的垂线段,分别记垂足为D,E。PD和PE的长度有什么关系?
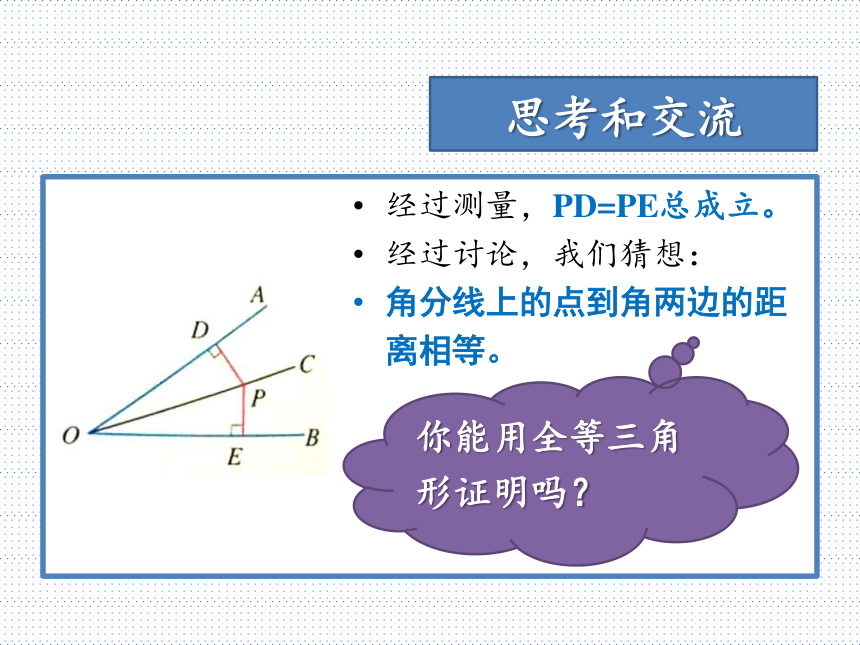
在OC上再取几个点试一下,并和你的伙伴交流结论,你们发现角平分线有什么性质?思考和交流经过测量,PD=PE总成立。
经过讨论,我们猜想:
角分线上的点到角两边的距离相等。你能用全等三角形证明吗?怎样证明几何命题?证明几何命题,先明确已知和求证。
已知:一个点在一个角的平分线上。
求证:这个点到这个角两边的距离相等。
为了更直观、清楚地表达题意,我们通常在证明前要画出图形,并用数学符号表示已知和求证。
由已知分析出证明途径,写出证明过程。给出图形和数学语言如图,已知∠AOC=∠BOC,点P在OC上,且PD⊥OA,PE⊥OB,垂足分别为D,E。
求证:PD=PE。证明过程角的平分线的性质角分线上的点到角两边的距离相等∵OC平分∠AOB,PD⊥OA,PE⊥OB
∴PD=PE动脑想一想如图,要在S区建一个集贸中心,使它到铁路、公路的距离相等,并且离公路与铁路的交叉处500m,这个集贸中心应建在哪里?角分线上的点到角两边的距离相等。
到角的两边的距离相等的点是否也在角的平分线上呢?动脑想一想画出几何图形,写出已知和求证,证明这个猜想。给出图形和数学语言如图,P是∠AOB上的一点,PD⊥OA于D,PE⊥OB于E,且PD=PE。
求证:OP是∠AOB的平分线。证明过程角的平分线的判定角的内部到角的两边距离相等的点在角的平分线上∵P是∠AOB内的一点,PD⊥OA,PE⊥OB,且PD=PE
∴OP是∠AOB的平分线我们之间就学习了三角形的角分线,之前谈到过,三条角分线一定交于一点,不过当时我们没有给出证明,而只是通过画图的方法给出了印证。
现在我们学习了角分线的性质和判定定理,怎样证明这个结论呢?我们先看下面的例题。动脑想一想如图,△ABC的平分线BM,CN相交于点P。
求证:点P到三边AB,BC,CA的距离相等。动脑想一想证明:
过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F。
∵BM是△ABC的角平分线,
点P在BM上
∴PD=PE,同理PE=PF
∴PD=PE=PF
即点P到三边AB,BC,CA的距离相等动脑想一想根据PF=PD,且PD⊥AB,PF⊥AC的事实,你现在能得到什么结论?
点P也在∠A的平分线上,也就是说,点A是三角形三条角平分线的交点。动脑想一想角分线的判定和性质点在角平分线上点到角两边的距离相等判定性质学完本节课你应该知道角的平分线尺规画角的平分线性质和判定点在角平分线上点到角两边的距离相等判定性质会证明动笔练一练如图,OP平分∠AOB,PA⊥OA于A,PB垂直于OB于B,下列结论一定成立的是( )
PA=PB
PO平分∠APB
OA=OB
以上都一定成立D动笔练一练如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
线段CD的中点
CD与过点O做CD垂线的交点
CD与∠AOB的平分线交点
CD上任意一点C动笔练一练如图,AD⊥OB于D,BC⊥OA于C,AD与BC相交于点P,若PA=PB,则∠1和∠2的大小关系是( )
∠1=∠2
∠1>∠2
∠1<∠2
无法确定A动笔练一练如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF。
求证:CF=EB。动笔练一练证明:
∵AD平分∠CAB
且DE⊥AB,∠C=90°(已知)
∴CD=DE
在Rt△CDF和Rt△EDB中,
CD=DE (已证)
DF=DB (已知)
∴ Rt△CDF≌Rt△EDB (HL)
∴ CF=EB课后练一练请同学们独立完成配套课后练习题。下课!谢谢同学们!
掌握角平分线的性质,会运用性质解决相关问题,并能证明这一命题。
掌握角平分线的判定定理,理解角平分线的判定定理和性质定理的关系。现在有一张用纸做的角,怎样不利用其他工具把它平分?
对折之后的折痕和这个角有什么关系?
如果是木板不能对折,该怎么平分?动脑想一想如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,则AC所在直线就是这个角的平分线。
你能说明这是为什么吗?动脑想一想证明:
在△ADC和△ABC 中
AB=AD(已知)
AC=AC(公共边相等)
DC=BC(已知)
∴ △ADC≌△ABC (SSS)
∴∠DAC=∠BAC(对应角相等)
即 AE平分∠BAD动脑想一想通过刚才的启发,你能想到怎样画出下面的角的平分线吗?动脑想一想BAO仅用尺规作图,已知∠AOB,求作∠AOB的平分线尺规法画角平分线BAO以点O为圆心,任意适当长度为半径画弧,交OA于点M,交OB于点NMN尺规法画角平分线BAO分别以点M,N为圆心,大于?MN的长度为半径画弧,两弧在∠AOB的内部交于点CMNC尺规法画角平分线BAO画射线OC,即为∠AOB的角平分线MNC思考和交流在你刚才画好的角平分线OC上任意取一点P,过点P画出OA和OB的垂线段,分别记垂足为D,E。PD和PE的长度有什么关系?
在OC上再取几个点试一下,并和你的伙伴交流结论,你们发现角平分线有什么性质?思考和交流经过测量,PD=PE总成立。
经过讨论,我们猜想:
角分线上的点到角两边的距离相等。你能用全等三角形证明吗?怎样证明几何命题?证明几何命题,先明确已知和求证。
已知:一个点在一个角的平分线上。
求证:这个点到这个角两边的距离相等。
为了更直观、清楚地表达题意,我们通常在证明前要画出图形,并用数学符号表示已知和求证。
由已知分析出证明途径,写出证明过程。给出图形和数学语言如图,已知∠AOC=∠BOC,点P在OC上,且PD⊥OA,PE⊥OB,垂足分别为D,E。
求证:PD=PE。证明过程角的平分线的性质角分线上的点到角两边的距离相等∵OC平分∠AOB,PD⊥OA,PE⊥OB
∴PD=PE动脑想一想如图,要在S区建一个集贸中心,使它到铁路、公路的距离相等,并且离公路与铁路的交叉处500m,这个集贸中心应建在哪里?角分线上的点到角两边的距离相等。
到角的两边的距离相等的点是否也在角的平分线上呢?动脑想一想画出几何图形,写出已知和求证,证明这个猜想。给出图形和数学语言如图,P是∠AOB上的一点,PD⊥OA于D,PE⊥OB于E,且PD=PE。
求证:OP是∠AOB的平分线。证明过程角的平分线的判定角的内部到角的两边距离相等的点在角的平分线上∵P是∠AOB内的一点,PD⊥OA,PE⊥OB,且PD=PE
∴OP是∠AOB的平分线我们之间就学习了三角形的角分线,之前谈到过,三条角分线一定交于一点,不过当时我们没有给出证明,而只是通过画图的方法给出了印证。
现在我们学习了角分线的性质和判定定理,怎样证明这个结论呢?我们先看下面的例题。动脑想一想如图,△ABC的平分线BM,CN相交于点P。
求证:点P到三边AB,BC,CA的距离相等。动脑想一想证明:
过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F。
∵BM是△ABC的角平分线,
点P在BM上
∴PD=PE,同理PE=PF
∴PD=PE=PF
即点P到三边AB,BC,CA的距离相等动脑想一想根据PF=PD,且PD⊥AB,PF⊥AC的事实,你现在能得到什么结论?
点P也在∠A的平分线上,也就是说,点A是三角形三条角平分线的交点。动脑想一想角分线的判定和性质点在角平分线上点到角两边的距离相等判定性质学完本节课你应该知道角的平分线尺规画角的平分线性质和判定点在角平分线上点到角两边的距离相等判定性质会证明动笔练一练如图,OP平分∠AOB,PA⊥OA于A,PB垂直于OB于B,下列结论一定成立的是( )
PA=PB
PO平分∠APB
OA=OB
以上都一定成立D动笔练一练如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )
线段CD的中点
CD与过点O做CD垂线的交点
CD与∠AOB的平分线交点
CD上任意一点C动笔练一练如图,AD⊥OB于D,BC⊥OA于C,AD与BC相交于点P,若PA=PB,则∠1和∠2的大小关系是( )
∠1=∠2
∠1>∠2
∠1<∠2
无法确定A动笔练一练如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF。
求证:CF=EB。动笔练一练证明:
∵AD平分∠CAB
且DE⊥AB,∠C=90°(已知)
∴CD=DE
在Rt△CDF和Rt△EDB中,
CD=DE (已证)
DF=DB (已知)
∴ Rt△CDF≌Rt△EDB (HL)
∴ CF=EB课后练一练请同学们独立完成配套课后练习题。下课!谢谢同学们!
