12.2 三角形全等的判定同步课时作业(1)
文档属性
| 名称 | 12.2 三角形全等的判定同步课时作业(1) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-09 10:59:57 | ||
图片预览




文档简介
12.2 三角形全等的判定同步课时作业(1)
姓名:___________班级:___________考号:___________
一、选择题
1.如图,用尺规作一个角等于已知角,其作图原理是:由△ODC≌△O’D’C’得∠AOB=∠A’O’B’,其依据的定理是( )
A. SSS B. SAS C. ASA D. AAS
2.如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE.可利用的是( )
A. ①或② B. ②或③ C. ③或① D. ①或④
3.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( )
A. AB=BC B. DC=BC C. AB=CD D. 以上都不对
4.如图所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有( )
A. 2对 B. 3对 C. 4对 D. 5对
5.如图,中,,,直接使用“SSS”可判定( )
A. ≌ B. ≌ C. ≌ D. ≌
6.如图,AB=AD,BE=DE,BC=DC,则图中全等三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
7.若在△ABC和△A′B′C′中,,则不正确的结论是( )
A. △ABC≌△A′B′C′ B. 三边对应相等
C. 三对角对应相等 D. △ABC与△A′B′C′不全等
8.如图,AB=DE,AC=DF,BC=EF,则∠D等于( )
A. 30° B. 50° C. 60° D. 100°
二、填空题
9.如图,AC=AD,BC=BD,则△ABC≌△______;应用的判定方法是(简写)______.
10.如图,若AB=DE,_____,BE=CF,则根据“SSS”可得△ABC≌△DEF.
11.如图,AB=AC,BD=CD,若∠B=28°则∠C=________ 度;
12.如图,小敏做了一个角平分仪ABCD,其中,,将仪器上的点A与的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是的平分线此角平分仪的画图原理是:根据仪器结构,可得≌,这样就有则说明这两个三角形全等的依据是______
13.如图,AC、BD相交于点O,AB=DC﹑AO=DO,请你补充一个条件,使得△AOB≌△DOC(SSS).你补充的条件是__________.
14.请完善下面说明三角形全等的推理过程:
如图,在△ABC和__________中,
∵ AB=AD (已知)
____=DC (已知)
AC=________ ________
∴ △ABC ≌ ________(SSS)
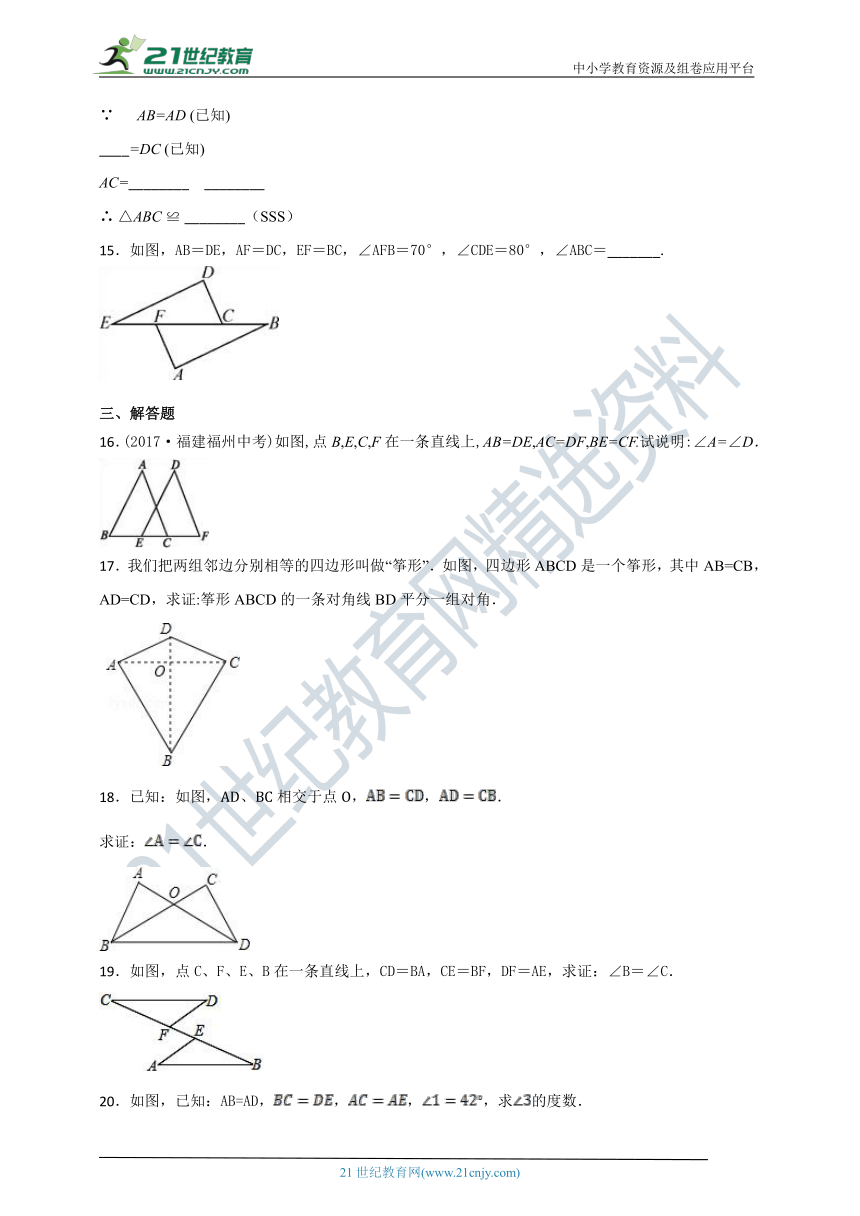
15.如图,AB=DE,AF=DC,EF=BC,∠AFB=70°,∠CDE=80°,∠ABC=_______.
三、解答题
16.(2017·福建福州中考)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.试说明:∠A=∠D.
17.我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,求证:筝形ABCD的一条对角线BD平分一组对角.
18.已知:如图,AD、BC相交于点O,,.
求证:.
19.如图,点C、F、E、B在一条直线上,CD=BA,CE=BF,DF=AE,求证:∠B=∠C.
20.如图,已知:AB=AD,,,,求的度数.
21.已知:∠AOB及边OB上一点C.求作:∠OCD,使得∠OCD=∠AOB.
要求:1.尺规作图,保留作图痕迹,不写作法;(说明:作出一个即可)
2.请你写出作图的依据.
22.如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
参考答案
1.A
【解析】分析:在做一个角等于已知角时,实际上作的是三边对应相等,根据三边对应相等两三角形全等,全等三角形的对应角相等可知所作的角等于已知角.
详解:在△OCD与△O′C′D′,
∵ ,
∴△OCD≌△O′C′D′(SSS),
∴∠A′O′B′=∠AOB,
显然运用的判定方法是SSS.
故选A.
点睛:本题考点是全等三角形的判定和性质的应用,熟练掌握全等三角形的判定和性质定理是解决本题的关键,本题是常考题,要熟练掌握
2.A
【解析】试题解析:由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE,
若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,
故①可以;
若添加AB=FE,则可直接证明两三角形的全等,故②可以,
若添加AE=BE,或BF=BE,均不能得出AB=FE,不可以利用SSS进行全等的证明,故③④不可以.
故选A.
3.C
【解析】试题解析:要利用“SSS”证明≌时,需
故选C.
4.C
【解析】因为AB=CD,AD=CB,根据SSS可以判定三角形ABD与三角形CDB全等,三角形ABC与三角形CDA,根据平行四边形的性质可得:AO=CO,BO=DO,再利用SSS可以判定三角形AOD和三角形COB全等,三角形AOB和三角形COD全等,共4对,故选C.
5.B
【解析】分析:根据已知条件和全等三角形的全等定理结合图形得出选项即可.
详解:根据AB=AC,BE=EC,AE=AE可以推出△ABE≌△AACE,理由是SSS,
其余△ABD≌△ACD,△BED≌△CED不能直接用SSS定理推出,△ABE和△EDC不全等,
故选:B.
点睛:本题考查了全等三角形的判定的应用,全等三角形的判定定理有SAS,AAS,ASA,SSS,题目比较好,难度适中.
6.C
【解析】在△ABE和△ADE中,,∴△ABE≌△ADE(SSS);
在△ABC和△ADC中,,∴△ABC≌△ADC(SSS);
在△BCE和△DCE中,,∴△BCE≌△DCE(SSS);
综上可得共有3对全等图形,
故选C.
7.D
【解析】三边对应比值为1,即三边对应相等,故B正确;
所以△ABC≌△A′B′C′,故A选项正确;
全等三角形对应角相等,故C选项正确;
D、因为两三角形全等,所以本选项错误,
故选D.
8.D
【解析】∵AB=DE,AC=DF,BC=EF, ∴△ABC≌△DEF, ∴∠A=∠D,在△ABC中,∠A=180°-50°-30°=100°, ∴∠D=100°,故选D.
9. △ABD SSS.
【解析】∵AC=AD,BC=BD,AB=AB(公共边),
∴△ABC≌△ABD(SSS).
10.AC=DF
【解析】试题解析: ,
,
,
又,
当时,根据可以判定
故答案为: .
11.28
【解析】连接线段AD
在△ABD与△ACD中,
∴△ABD≌△ACD
∴∠B=∠C
又∵∠B=28°
∴∠C=28°
故答案为28°
12.SSS
【解析】
【分析】
在△ADC和△ABC中,由于AC为公共边,AB=AD,BC=DC,利用SSS定理可判定△ADC≌△ABC,进而得到∠DAC=∠BAC,即∠QAE=∠PAE.
【详解】
在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS).
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故答案为:SSS.
【点睛】
本题考查了全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.
13.BO=CO
【解析】添加的条件是BO=CO,理由是:
∵在△AOB和△DOC中,
∴△AOB≌△DOC(SSS),
故答案为:BO=CO.
14. △ADC BC AC 公共边 △ADC
【解析】在△ABC和△ADC中,
∵AB=AD (已知),
BC=DC (已知),
AC=AC(公共边),
∴ △ABC ≌△ADC(SSS),
故答案为:△ADC, BC , AC,公共边, △ADC.
15.30°
【解析】试题解析:∵CF=BE,
∴CF+EF=BE+EF,
∴CE=BF,
在△AFB和△DEC中,
∴△AFB≌△DEC(SSS),
∴在△AFB中,
故答案为:
16.理由见解析.
【解析】试题分析:根据题意得出BC=EF,然后结合已知条件得出△ABC和△DEF全等,从而得出答案.
试题解析:因为BE=CF,所以BE+CE=CF+CE, 所以BC=EF.
在△ABC和△DEF中, 所以△ABC≌△DEF(SSS),所以∠A=∠D.
17.证明见解析
【解析】试题分析:首先根据题意利用SSS来判定△ABD和△CBD全等,然后得出∠ADB=∠CBD,∠ABD=∠CBD,从而得出结论.
试题解析:在△ABD和△CBD中AB=CB AD=CD BD=BD
∴△ABD≌△CBD(SSS)
∴∠ADB=∠CBD ∠ABD=∠CBD
即BD平分一组对角
18.证明见解析
【解析】
【分析】
根据SSS推出≌,然后由全等三角的对应角相等即可证明结论.
【详解】
在和中,
≌,
.
【点睛】
本题考查了全等三角形性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.
19.见解析
【解析】分析:首先证明CF=BE,然后证明△CDF≌△BAE,进而可得∠B =∠C.
详解:∵CE=BF,∴CF=BE,
在△BAE与△CDF中,
,
∴ △BAE≌△CDF(SSS),
∴∠B=∠C.
点睛:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
20.42°
【解析】
【分析】
利用SSS证明△ABC≌△ADE,根据全等三角形对应角相等可得∠ADE=∠B,继而可以求得∠3=∠1.
【详解】
在和中,
,
≌ ,
,
,
,
.
【点睛】
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题的关键.
21.(1)见解析;(2)见解析.
【解析】分析:(1)根据作一个角等于一个角的步骤,以O为顶点,作∠OCD=∠AOB即可;(2)由作法知,OE=OF=OM=ON,EF=MN,依据“SSS”可知△OEF≌△CMN,从而可知∠OCD=∠AOB.
详解:(1)如图所示,∠OCD即为所求;
(2)作图的依据为SSS.
点睛:本题考查了作一个角等于已知角和全等三角形的判定与性质,熟练掌握作一个角等于已知角得作图步骤和全等三角形的判定方法是解答本题的关键.全等三角形的判定方法有:“SAS”、“ASA”、“AAS”、“SSS” “HL”几种方法.
22.(1)证明见解析;(2)37°
【解析】分析:(1)先证明AC=DF,再运用SSS证明△ABC≌△DEF;
(2)根据三角形内角和定理可求∠ACB=37°,由(1)知∠F=∠ACB,从而可得结论.
解析:(1)∵AC=AD+DC, DF=DC+CF,且AD=CF
∴AC=DF
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
(2)由(1)可知,∠F=∠ACB
∵∠A=55°,∠B=88°
∴∠ACB=180°-(∠A+∠B)=180°-(55°+88°)=37°
∴∠F=∠ACB=37°
点睛:本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
12.2 三角形全等的判定同步课时作业(1)
姓名:___________班级:___________考号:___________
一、选择题
1.如图,用尺规作一个角等于已知角,其作图原理是:由△ODC≌△O’D’C’得∠AOB=∠A’O’B’,其依据的定理是( )
A. SSS B. SAS C. ASA D. AAS
2.如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE.可利用的是( )
A. ①或② B. ②或③ C. ③或① D. ①或④
3.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( )
A. AB=BC B. DC=BC C. AB=CD D. 以上都不对
4.如图所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有( )
A. 2对 B. 3对 C. 4对 D. 5对
5.如图,中,,,直接使用“SSS”可判定( )
A. ≌ B. ≌ C. ≌ D. ≌
6.如图,AB=AD,BE=DE,BC=DC,则图中全等三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
7.若在△ABC和△A′B′C′中,,则不正确的结论是( )
A. △ABC≌△A′B′C′ B. 三边对应相等
C. 三对角对应相等 D. △ABC与△A′B′C′不全等
8.如图,AB=DE,AC=DF,BC=EF,则∠D等于( )
A. 30° B. 50° C. 60° D. 100°
二、填空题
9.如图,AC=AD,BC=BD,则△ABC≌△______;应用的判定方法是(简写)______.
10.如图,若AB=DE,_____,BE=CF,则根据“SSS”可得△ABC≌△DEF.
11.如图,AB=AC,BD=CD,若∠B=28°则∠C=________ 度;
12.如图,小敏做了一个角平分仪ABCD,其中,,将仪器上的点A与的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是的平分线此角平分仪的画图原理是:根据仪器结构,可得≌,这样就有则说明这两个三角形全等的依据是______
13.如图,AC、BD相交于点O,AB=DC﹑AO=DO,请你补充一个条件,使得△AOB≌△DOC(SSS).你补充的条件是__________.
14.请完善下面说明三角形全等的推理过程:
如图,在△ABC和__________中,
∵ AB=AD (已知)
____=DC (已知)
AC=________ ________
∴ △ABC ≌ ________(SSS)
15.如图,AB=DE,AF=DC,EF=BC,∠AFB=70°,∠CDE=80°,∠ABC=_______.
三、解答题
16.(2017·福建福州中考)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.试说明:∠A=∠D.
17.我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,求证:筝形ABCD的一条对角线BD平分一组对角.
18.已知:如图,AD、BC相交于点O,,.
求证:.
19.如图,点C、F、E、B在一条直线上,CD=BA,CE=BF,DF=AE,求证:∠B=∠C.
20.如图,已知:AB=AD,,,,求的度数.
21.已知:∠AOB及边OB上一点C.求作:∠OCD,使得∠OCD=∠AOB.
要求:1.尺规作图,保留作图痕迹,不写作法;(说明:作出一个即可)
2.请你写出作图的依据.
22.如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
参考答案
1.A
【解析】分析:在做一个角等于已知角时,实际上作的是三边对应相等,根据三边对应相等两三角形全等,全等三角形的对应角相等可知所作的角等于已知角.
详解:在△OCD与△O′C′D′,
∵ ,
∴△OCD≌△O′C′D′(SSS),
∴∠A′O′B′=∠AOB,
显然运用的判定方法是SSS.
故选A.
点睛:本题考点是全等三角形的判定和性质的应用,熟练掌握全等三角形的判定和性质定理是解决本题的关键,本题是常考题,要熟练掌握
2.A
【解析】试题解析:由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE,
若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,
故①可以;
若添加AB=FE,则可直接证明两三角形的全等,故②可以,
若添加AE=BE,或BF=BE,均不能得出AB=FE,不可以利用SSS进行全等的证明,故③④不可以.
故选A.
3.C
【解析】试题解析:要利用“SSS”证明≌时,需
故选C.
4.C
【解析】因为AB=CD,AD=CB,根据SSS可以判定三角形ABD与三角形CDB全等,三角形ABC与三角形CDA,根据平行四边形的性质可得:AO=CO,BO=DO,再利用SSS可以判定三角形AOD和三角形COB全等,三角形AOB和三角形COD全等,共4对,故选C.
5.B
【解析】分析:根据已知条件和全等三角形的全等定理结合图形得出选项即可.
详解:根据AB=AC,BE=EC,AE=AE可以推出△ABE≌△AACE,理由是SSS,
其余△ABD≌△ACD,△BED≌△CED不能直接用SSS定理推出,△ABE和△EDC不全等,
故选:B.
点睛:本题考查了全等三角形的判定的应用,全等三角形的判定定理有SAS,AAS,ASA,SSS,题目比较好,难度适中.
6.C
【解析】在△ABE和△ADE中,,∴△ABE≌△ADE(SSS);
在△ABC和△ADC中,,∴△ABC≌△ADC(SSS);
在△BCE和△DCE中,,∴△BCE≌△DCE(SSS);
综上可得共有3对全等图形,
故选C.
7.D
【解析】三边对应比值为1,即三边对应相等,故B正确;
所以△ABC≌△A′B′C′,故A选项正确;
全等三角形对应角相等,故C选项正确;
D、因为两三角形全等,所以本选项错误,
故选D.
8.D
【解析】∵AB=DE,AC=DF,BC=EF, ∴△ABC≌△DEF, ∴∠A=∠D,在△ABC中,∠A=180°-50°-30°=100°, ∴∠D=100°,故选D.
9. △ABD SSS.
【解析】∵AC=AD,BC=BD,AB=AB(公共边),
∴△ABC≌△ABD(SSS).
10.AC=DF
【解析】试题解析: ,
,
,
又,
当时,根据可以判定
故答案为: .
11.28
【解析】连接线段AD
在△ABD与△ACD中,
∴△ABD≌△ACD
∴∠B=∠C
又∵∠B=28°
∴∠C=28°
故答案为28°
12.SSS
【解析】
【分析】
在△ADC和△ABC中,由于AC为公共边,AB=AD,BC=DC,利用SSS定理可判定△ADC≌△ABC,进而得到∠DAC=∠BAC,即∠QAE=∠PAE.
【详解】
在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS).
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故答案为:SSS.
【点睛】
本题考查了全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.
13.BO=CO
【解析】添加的条件是BO=CO,理由是:
∵在△AOB和△DOC中,
∴△AOB≌△DOC(SSS),
故答案为:BO=CO.
14. △ADC BC AC 公共边 △ADC
【解析】在△ABC和△ADC中,
∵AB=AD (已知),
BC=DC (已知),
AC=AC(公共边),
∴ △ABC ≌△ADC(SSS),
故答案为:△ADC, BC , AC,公共边, △ADC.
15.30°
【解析】试题解析:∵CF=BE,
∴CF+EF=BE+EF,
∴CE=BF,
在△AFB和△DEC中,
∴△AFB≌△DEC(SSS),
∴在△AFB中,
故答案为:
16.理由见解析.
【解析】试题分析:根据题意得出BC=EF,然后结合已知条件得出△ABC和△DEF全等,从而得出答案.
试题解析:因为BE=CF,所以BE+CE=CF+CE, 所以BC=EF.
在△ABC和△DEF中, 所以△ABC≌△DEF(SSS),所以∠A=∠D.
17.证明见解析
【解析】试题分析:首先根据题意利用SSS来判定△ABD和△CBD全等,然后得出∠ADB=∠CBD,∠ABD=∠CBD,从而得出结论.
试题解析:在△ABD和△CBD中AB=CB AD=CD BD=BD
∴△ABD≌△CBD(SSS)
∴∠ADB=∠CBD ∠ABD=∠CBD
即BD平分一组对角
18.证明见解析
【解析】
【分析】
根据SSS推出≌,然后由全等三角的对应角相等即可证明结论.
【详解】
在和中,
≌,
.
【点睛】
本题考查了全等三角形性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.
19.见解析
【解析】分析:首先证明CF=BE,然后证明△CDF≌△BAE,进而可得∠B =∠C.
详解:∵CE=BF,∴CF=BE,
在△BAE与△CDF中,
,
∴ △BAE≌△CDF(SSS),
∴∠B=∠C.
点睛:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
20.42°
【解析】
【分析】
利用SSS证明△ABC≌△ADE,根据全等三角形对应角相等可得∠ADE=∠B,继而可以求得∠3=∠1.
【详解】
在和中,
,
≌ ,
,
,
,
.
【点睛】
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题的关键.
21.(1)见解析;(2)见解析.
【解析】分析:(1)根据作一个角等于一个角的步骤,以O为顶点,作∠OCD=∠AOB即可;(2)由作法知,OE=OF=OM=ON,EF=MN,依据“SSS”可知△OEF≌△CMN,从而可知∠OCD=∠AOB.
详解:(1)如图所示,∠OCD即为所求;
(2)作图的依据为SSS.
点睛:本题考查了作一个角等于已知角和全等三角形的判定与性质,熟练掌握作一个角等于已知角得作图步骤和全等三角形的判定方法是解答本题的关键.全等三角形的判定方法有:“SAS”、“ASA”、“AAS”、“SSS” “HL”几种方法.
22.(1)证明见解析;(2)37°
【解析】分析:(1)先证明AC=DF,再运用SSS证明△ABC≌△DEF;
(2)根据三角形内角和定理可求∠ACB=37°,由(1)知∠F=∠ACB,从而可得结论.
解析:(1)∵AC=AD+DC, DF=DC+CF,且AD=CF
∴AC=DF
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
(2)由(1)可知,∠F=∠ACB
∵∠A=55°,∠B=88°
∴∠ACB=180°-(∠A+∠B)=180°-(55°+88°)=37°
∴∠F=∠ACB=37°
点睛:本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
姓名:___________班级:___________考号:___________
一、选择题
1.如图,用尺规作一个角等于已知角,其作图原理是:由△ODC≌△O’D’C’得∠AOB=∠A’O’B’,其依据的定理是( )
A. SSS B. SAS C. ASA D. AAS
2.如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE.可利用的是( )
A. ①或② B. ②或③ C. ③或① D. ①或④
3.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( )
A. AB=BC B. DC=BC C. AB=CD D. 以上都不对
4.如图所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有( )
A. 2对 B. 3对 C. 4对 D. 5对
5.如图,中,,,直接使用“SSS”可判定( )
A. ≌ B. ≌ C. ≌ D. ≌
6.如图,AB=AD,BE=DE,BC=DC,则图中全等三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
7.若在△ABC和△A′B′C′中,,则不正确的结论是( )
A. △ABC≌△A′B′C′ B. 三边对应相等
C. 三对角对应相等 D. △ABC与△A′B′C′不全等
8.如图,AB=DE,AC=DF,BC=EF,则∠D等于( )
A. 30° B. 50° C. 60° D. 100°
二、填空题
9.如图,AC=AD,BC=BD,则△ABC≌△______;应用的判定方法是(简写)______.
10.如图,若AB=DE,_____,BE=CF,则根据“SSS”可得△ABC≌△DEF.
11.如图,AB=AC,BD=CD,若∠B=28°则∠C=________ 度;
12.如图,小敏做了一个角平分仪ABCD,其中,,将仪器上的点A与的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是的平分线此角平分仪的画图原理是:根据仪器结构,可得≌,这样就有则说明这两个三角形全等的依据是______
13.如图,AC、BD相交于点O,AB=DC﹑AO=DO,请你补充一个条件,使得△AOB≌△DOC(SSS).你补充的条件是__________.
14.请完善下面说明三角形全等的推理过程:
如图,在△ABC和__________中,
∵ AB=AD (已知)
____=DC (已知)
AC=________ ________
∴ △ABC ≌ ________(SSS)
15.如图,AB=DE,AF=DC,EF=BC,∠AFB=70°,∠CDE=80°,∠ABC=_______.
三、解答题
16.(2017·福建福州中考)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.试说明:∠A=∠D.
17.我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,求证:筝形ABCD的一条对角线BD平分一组对角.
18.已知:如图,AD、BC相交于点O,,.
求证:.
19.如图,点C、F、E、B在一条直线上,CD=BA,CE=BF,DF=AE,求证:∠B=∠C.
20.如图,已知:AB=AD,,,,求的度数.
21.已知:∠AOB及边OB上一点C.求作:∠OCD,使得∠OCD=∠AOB.
要求:1.尺规作图,保留作图痕迹,不写作法;(说明:作出一个即可)
2.请你写出作图的依据.
22.如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
参考答案
1.A
【解析】分析:在做一个角等于已知角时,实际上作的是三边对应相等,根据三边对应相等两三角形全等,全等三角形的对应角相等可知所作的角等于已知角.
详解:在△OCD与△O′C′D′,
∵ ,
∴△OCD≌△O′C′D′(SSS),
∴∠A′O′B′=∠AOB,
显然运用的判定方法是SSS.
故选A.
点睛:本题考点是全等三角形的判定和性质的应用,熟练掌握全等三角形的判定和性质定理是解决本题的关键,本题是常考题,要熟练掌握
2.A
【解析】试题解析:由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE,
若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,
故①可以;
若添加AB=FE,则可直接证明两三角形的全等,故②可以,
若添加AE=BE,或BF=BE,均不能得出AB=FE,不可以利用SSS进行全等的证明,故③④不可以.
故选A.
3.C
【解析】试题解析:要利用“SSS”证明≌时,需
故选C.
4.C
【解析】因为AB=CD,AD=CB,根据SSS可以判定三角形ABD与三角形CDB全等,三角形ABC与三角形CDA,根据平行四边形的性质可得:AO=CO,BO=DO,再利用SSS可以判定三角形AOD和三角形COB全等,三角形AOB和三角形COD全等,共4对,故选C.
5.B
【解析】分析:根据已知条件和全等三角形的全等定理结合图形得出选项即可.
详解:根据AB=AC,BE=EC,AE=AE可以推出△ABE≌△AACE,理由是SSS,
其余△ABD≌△ACD,△BED≌△CED不能直接用SSS定理推出,△ABE和△EDC不全等,
故选:B.
点睛:本题考查了全等三角形的判定的应用,全等三角形的判定定理有SAS,AAS,ASA,SSS,题目比较好,难度适中.
6.C
【解析】在△ABE和△ADE中,,∴△ABE≌△ADE(SSS);
在△ABC和△ADC中,,∴△ABC≌△ADC(SSS);
在△BCE和△DCE中,,∴△BCE≌△DCE(SSS);
综上可得共有3对全等图形,
故选C.
7.D
【解析】三边对应比值为1,即三边对应相等,故B正确;
所以△ABC≌△A′B′C′,故A选项正确;
全等三角形对应角相等,故C选项正确;
D、因为两三角形全等,所以本选项错误,
故选D.
8.D
【解析】∵AB=DE,AC=DF,BC=EF, ∴△ABC≌△DEF, ∴∠A=∠D,在△ABC中,∠A=180°-50°-30°=100°, ∴∠D=100°,故选D.
9. △ABD SSS.
【解析】∵AC=AD,BC=BD,AB=AB(公共边),
∴△ABC≌△ABD(SSS).
10.AC=DF
【解析】试题解析: ,
,
,
又,
当时,根据可以判定
故答案为: .
11.28
【解析】连接线段AD
在△ABD与△ACD中,
∴△ABD≌△ACD
∴∠B=∠C
又∵∠B=28°
∴∠C=28°
故答案为28°
12.SSS
【解析】
【分析】
在△ADC和△ABC中,由于AC为公共边,AB=AD,BC=DC,利用SSS定理可判定△ADC≌△ABC,进而得到∠DAC=∠BAC,即∠QAE=∠PAE.
【详解】
在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS).
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故答案为:SSS.
【点睛】
本题考查了全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.
13.BO=CO
【解析】添加的条件是BO=CO,理由是:
∵在△AOB和△DOC中,
∴△AOB≌△DOC(SSS),
故答案为:BO=CO.
14. △ADC BC AC 公共边 △ADC
【解析】在△ABC和△ADC中,
∵AB=AD (已知),
BC=DC (已知),
AC=AC(公共边),
∴ △ABC ≌△ADC(SSS),
故答案为:△ADC, BC , AC,公共边, △ADC.
15.30°
【解析】试题解析:∵CF=BE,
∴CF+EF=BE+EF,
∴CE=BF,
在△AFB和△DEC中,
∴△AFB≌△DEC(SSS),
∴在△AFB中,
故答案为:
16.理由见解析.
【解析】试题分析:根据题意得出BC=EF,然后结合已知条件得出△ABC和△DEF全等,从而得出答案.
试题解析:因为BE=CF,所以BE+CE=CF+CE, 所以BC=EF.
在△ABC和△DEF中, 所以△ABC≌△DEF(SSS),所以∠A=∠D.
17.证明见解析
【解析】试题分析:首先根据题意利用SSS来判定△ABD和△CBD全等,然后得出∠ADB=∠CBD,∠ABD=∠CBD,从而得出结论.
试题解析:在△ABD和△CBD中AB=CB AD=CD BD=BD
∴△ABD≌△CBD(SSS)
∴∠ADB=∠CBD ∠ABD=∠CBD
即BD平分一组对角
18.证明见解析
【解析】
【分析】
根据SSS推出≌,然后由全等三角的对应角相等即可证明结论.
【详解】
在和中,
≌,
.
【点睛】
本题考查了全等三角形性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.
19.见解析
【解析】分析:首先证明CF=BE,然后证明△CDF≌△BAE,进而可得∠B =∠C.
详解:∵CE=BF,∴CF=BE,
在△BAE与△CDF中,
,
∴ △BAE≌△CDF(SSS),
∴∠B=∠C.
点睛:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
20.42°
【解析】
【分析】
利用SSS证明△ABC≌△ADE,根据全等三角形对应角相等可得∠ADE=∠B,继而可以求得∠3=∠1.
【详解】
在和中,
,
≌ ,
,
,
,
.
【点睛】
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题的关键.
21.(1)见解析;(2)见解析.
【解析】分析:(1)根据作一个角等于一个角的步骤,以O为顶点,作∠OCD=∠AOB即可;(2)由作法知,OE=OF=OM=ON,EF=MN,依据“SSS”可知△OEF≌△CMN,从而可知∠OCD=∠AOB.
详解:(1)如图所示,∠OCD即为所求;
(2)作图的依据为SSS.
点睛:本题考查了作一个角等于已知角和全等三角形的判定与性质,熟练掌握作一个角等于已知角得作图步骤和全等三角形的判定方法是解答本题的关键.全等三角形的判定方法有:“SAS”、“ASA”、“AAS”、“SSS” “HL”几种方法.
22.(1)证明见解析;(2)37°
【解析】分析:(1)先证明AC=DF,再运用SSS证明△ABC≌△DEF;
(2)根据三角形内角和定理可求∠ACB=37°,由(1)知∠F=∠ACB,从而可得结论.
解析:(1)∵AC=AD+DC, DF=DC+CF,且AD=CF
∴AC=DF
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
(2)由(1)可知,∠F=∠ACB
∵∠A=55°,∠B=88°
∴∠ACB=180°-(∠A+∠B)=180°-(55°+88°)=37°
∴∠F=∠ACB=37°
点睛:本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
12.2 三角形全等的判定同步课时作业(1)
姓名:___________班级:___________考号:___________
一、选择题
1.如图,用尺规作一个角等于已知角,其作图原理是:由△ODC≌△O’D’C’得∠AOB=∠A’O’B’,其依据的定理是( )
A. SSS B. SAS C. ASA D. AAS
2.如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE.可利用的是( )
A. ①或② B. ②或③ C. ③或① D. ①或④
3.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( )
A. AB=BC B. DC=BC C. AB=CD D. 以上都不对
4.如图所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有( )
A. 2对 B. 3对 C. 4对 D. 5对
5.如图,中,,,直接使用“SSS”可判定( )
A. ≌ B. ≌ C. ≌ D. ≌
6.如图,AB=AD,BE=DE,BC=DC,则图中全等三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
7.若在△ABC和△A′B′C′中,,则不正确的结论是( )
A. △ABC≌△A′B′C′ B. 三边对应相等
C. 三对角对应相等 D. △ABC与△A′B′C′不全等
8.如图,AB=DE,AC=DF,BC=EF,则∠D等于( )
A. 30° B. 50° C. 60° D. 100°
二、填空题
9.如图,AC=AD,BC=BD,则△ABC≌△______;应用的判定方法是(简写)______.
10.如图,若AB=DE,_____,BE=CF,则根据“SSS”可得△ABC≌△DEF.
11.如图,AB=AC,BD=CD,若∠B=28°则∠C=________ 度;
12.如图,小敏做了一个角平分仪ABCD,其中,,将仪器上的点A与的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是的平分线此角平分仪的画图原理是:根据仪器结构,可得≌,这样就有则说明这两个三角形全等的依据是______
13.如图,AC、BD相交于点O,AB=DC﹑AO=DO,请你补充一个条件,使得△AOB≌△DOC(SSS).你补充的条件是__________.
14.请完善下面说明三角形全等的推理过程:
如图,在△ABC和__________中,
∵ AB=AD (已知)
____=DC (已知)
AC=________ ________
∴ △ABC ≌ ________(SSS)
15.如图,AB=DE,AF=DC,EF=BC,∠AFB=70°,∠CDE=80°,∠ABC=_______.
三、解答题
16.(2017·福建福州中考)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.试说明:∠A=∠D.
17.我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,求证:筝形ABCD的一条对角线BD平分一组对角.
18.已知:如图,AD、BC相交于点O,,.
求证:.
19.如图,点C、F、E、B在一条直线上,CD=BA,CE=BF,DF=AE,求证:∠B=∠C.
20.如图,已知:AB=AD,,,,求的度数.
21.已知:∠AOB及边OB上一点C.求作:∠OCD,使得∠OCD=∠AOB.
要求:1.尺规作图,保留作图痕迹,不写作法;(说明:作出一个即可)
2.请你写出作图的依据.
22.如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
参考答案
1.A
【解析】分析:在做一个角等于已知角时,实际上作的是三边对应相等,根据三边对应相等两三角形全等,全等三角形的对应角相等可知所作的角等于已知角.
详解:在△OCD与△O′C′D′,
∵ ,
∴△OCD≌△O′C′D′(SSS),
∴∠A′O′B′=∠AOB,
显然运用的判定方法是SSS.
故选A.
点睛:本题考点是全等三角形的判定和性质的应用,熟练掌握全等三角形的判定和性质定理是解决本题的关键,本题是常考题,要熟练掌握
2.A
【解析】试题解析:由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE,
若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,
故①可以;
若添加AB=FE,则可直接证明两三角形的全等,故②可以,
若添加AE=BE,或BF=BE,均不能得出AB=FE,不可以利用SSS进行全等的证明,故③④不可以.
故选A.
3.C
【解析】试题解析:要利用“SSS”证明≌时,需
故选C.
4.C
【解析】因为AB=CD,AD=CB,根据SSS可以判定三角形ABD与三角形CDB全等,三角形ABC与三角形CDA,根据平行四边形的性质可得:AO=CO,BO=DO,再利用SSS可以判定三角形AOD和三角形COB全等,三角形AOB和三角形COD全等,共4对,故选C.
5.B
【解析】分析:根据已知条件和全等三角形的全等定理结合图形得出选项即可.
详解:根据AB=AC,BE=EC,AE=AE可以推出△ABE≌△AACE,理由是SSS,
其余△ABD≌△ACD,△BED≌△CED不能直接用SSS定理推出,△ABE和△EDC不全等,
故选:B.
点睛:本题考查了全等三角形的判定的应用,全等三角形的判定定理有SAS,AAS,ASA,SSS,题目比较好,难度适中.
6.C
【解析】在△ABE和△ADE中,,∴△ABE≌△ADE(SSS);
在△ABC和△ADC中,,∴△ABC≌△ADC(SSS);
在△BCE和△DCE中,,∴△BCE≌△DCE(SSS);
综上可得共有3对全等图形,
故选C.
7.D
【解析】三边对应比值为1,即三边对应相等,故B正确;
所以△ABC≌△A′B′C′,故A选项正确;
全等三角形对应角相等,故C选项正确;
D、因为两三角形全等,所以本选项错误,
故选D.
8.D
【解析】∵AB=DE,AC=DF,BC=EF, ∴△ABC≌△DEF, ∴∠A=∠D,在△ABC中,∠A=180°-50°-30°=100°, ∴∠D=100°,故选D.
9. △ABD SSS.
【解析】∵AC=AD,BC=BD,AB=AB(公共边),
∴△ABC≌△ABD(SSS).
10.AC=DF
【解析】试题解析: ,
,
,
又,
当时,根据可以判定
故答案为: .
11.28
【解析】连接线段AD
在△ABD与△ACD中,
∴△ABD≌△ACD
∴∠B=∠C
又∵∠B=28°
∴∠C=28°
故答案为28°
12.SSS
【解析】
【分析】
在△ADC和△ABC中,由于AC为公共边,AB=AD,BC=DC,利用SSS定理可判定△ADC≌△ABC,进而得到∠DAC=∠BAC,即∠QAE=∠PAE.
【详解】
在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS).
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故答案为:SSS.
【点睛】
本题考查了全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.
13.BO=CO
【解析】添加的条件是BO=CO,理由是:
∵在△AOB和△DOC中,
∴△AOB≌△DOC(SSS),
故答案为:BO=CO.
14. △ADC BC AC 公共边 △ADC
【解析】在△ABC和△ADC中,
∵AB=AD (已知),
BC=DC (已知),
AC=AC(公共边),
∴ △ABC ≌△ADC(SSS),
故答案为:△ADC, BC , AC,公共边, △ADC.
15.30°
【解析】试题解析:∵CF=BE,
∴CF+EF=BE+EF,
∴CE=BF,
在△AFB和△DEC中,
∴△AFB≌△DEC(SSS),
∴在△AFB中,
故答案为:
16.理由见解析.
【解析】试题分析:根据题意得出BC=EF,然后结合已知条件得出△ABC和△DEF全等,从而得出答案.
试题解析:因为BE=CF,所以BE+CE=CF+CE, 所以BC=EF.
在△ABC和△DEF中, 所以△ABC≌△DEF(SSS),所以∠A=∠D.
17.证明见解析
【解析】试题分析:首先根据题意利用SSS来判定△ABD和△CBD全等,然后得出∠ADB=∠CBD,∠ABD=∠CBD,从而得出结论.
试题解析:在△ABD和△CBD中AB=CB AD=CD BD=BD
∴△ABD≌△CBD(SSS)
∴∠ADB=∠CBD ∠ABD=∠CBD
即BD平分一组对角
18.证明见解析
【解析】
【分析】
根据SSS推出≌,然后由全等三角的对应角相等即可证明结论.
【详解】
在和中,
≌,
.
【点睛】
本题考查了全等三角形性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.
19.见解析
【解析】分析:首先证明CF=BE,然后证明△CDF≌△BAE,进而可得∠B =∠C.
详解:∵CE=BF,∴CF=BE,
在△BAE与△CDF中,
,
∴ △BAE≌△CDF(SSS),
∴∠B=∠C.
点睛:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
20.42°
【解析】
【分析】
利用SSS证明△ABC≌△ADE,根据全等三角形对应角相等可得∠ADE=∠B,继而可以求得∠3=∠1.
【详解】
在和中,
,
≌ ,
,
,
,
.
【点睛】
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题的关键.
21.(1)见解析;(2)见解析.
【解析】分析:(1)根据作一个角等于一个角的步骤,以O为顶点,作∠OCD=∠AOB即可;(2)由作法知,OE=OF=OM=ON,EF=MN,依据“SSS”可知△OEF≌△CMN,从而可知∠OCD=∠AOB.
详解:(1)如图所示,∠OCD即为所求;
(2)作图的依据为SSS.
点睛:本题考查了作一个角等于已知角和全等三角形的判定与性质,熟练掌握作一个角等于已知角得作图步骤和全等三角形的判定方法是解答本题的关键.全等三角形的判定方法有:“SAS”、“ASA”、“AAS”、“SSS” “HL”几种方法.
22.(1)证明见解析;(2)37°
【解析】分析:(1)先证明AC=DF,再运用SSS证明△ABC≌△DEF;
(2)根据三角形内角和定理可求∠ACB=37°,由(1)知∠F=∠ACB,从而可得结论.
解析:(1)∵AC=AD+DC, DF=DC+CF,且AD=CF
∴AC=DF
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
(2)由(1)可知,∠F=∠ACB
∵∠A=55°,∠B=88°
∴∠ACB=180°-(∠A+∠B)=180°-(55°+88°)=37°
∴∠F=∠ACB=37°
点睛:本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
