函数的奇偶性

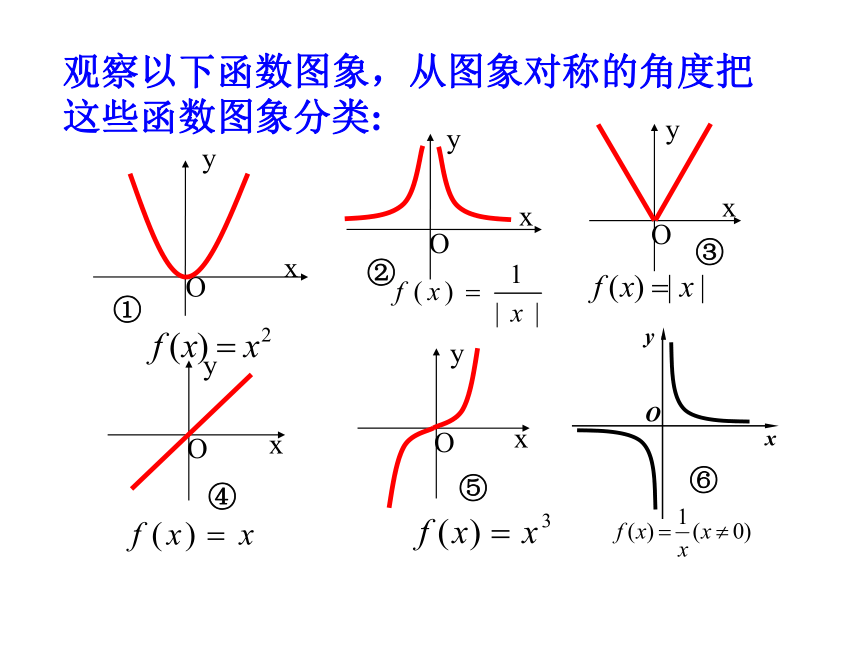
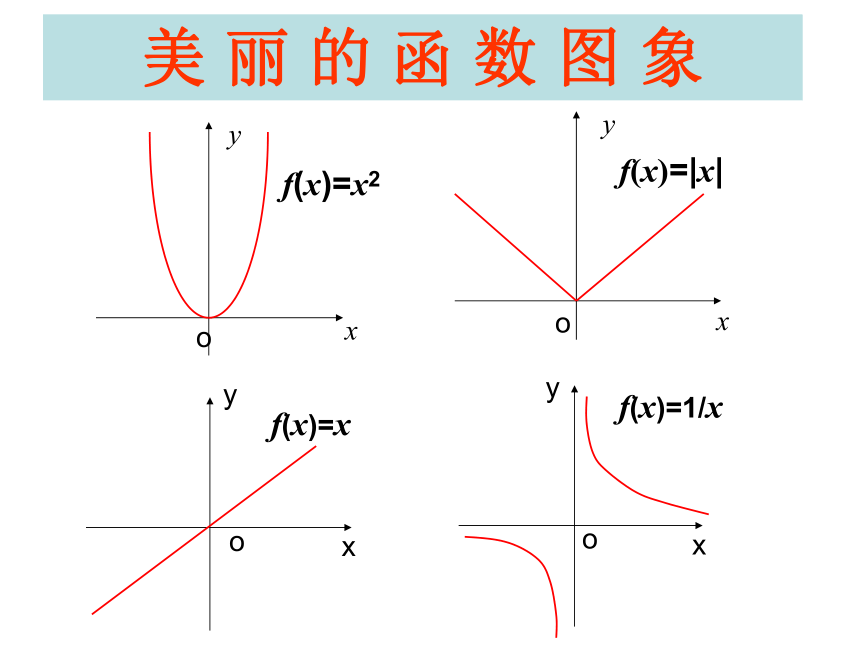
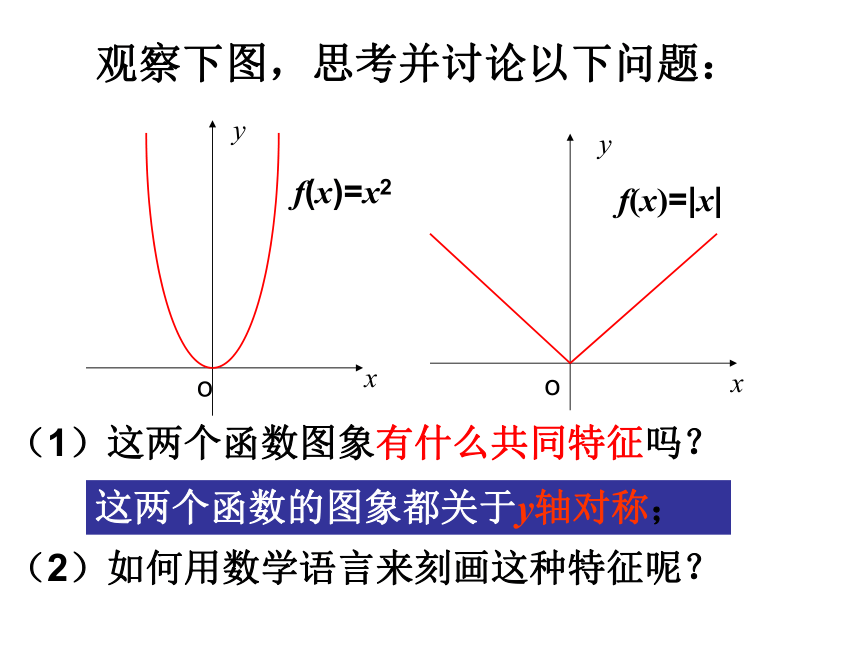
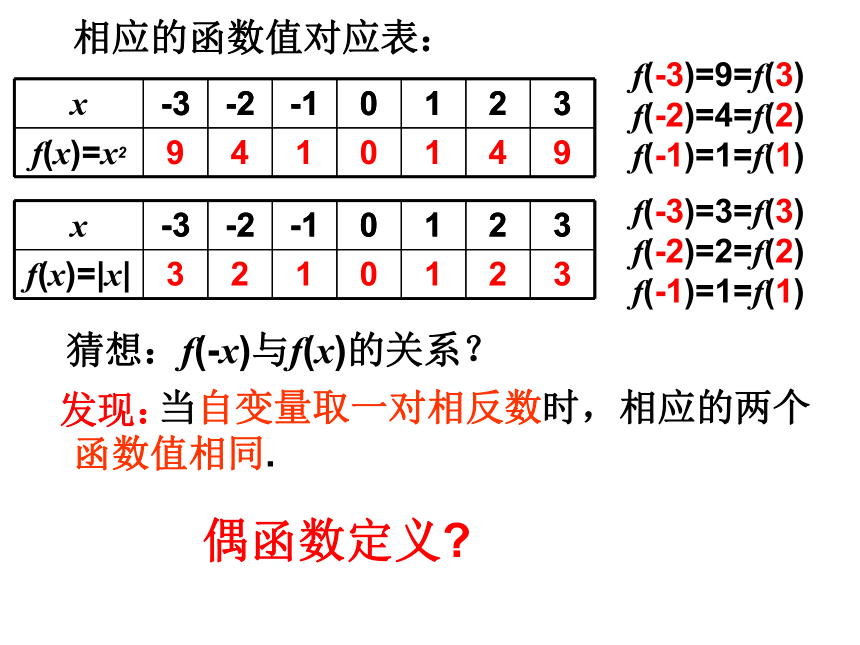
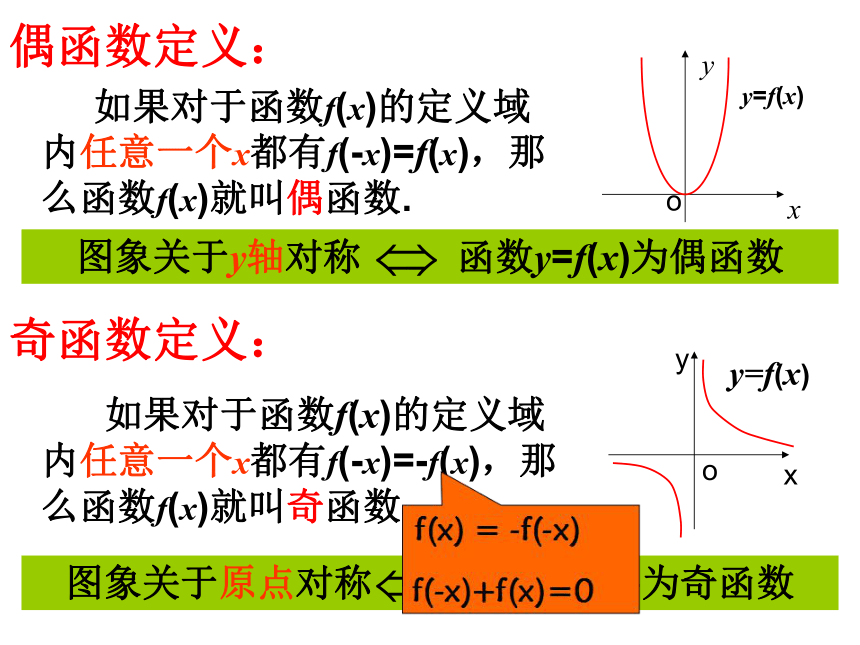
课件37张PPT。函数的奇偶性从生活中这些图片中你感受到了什么？1.请欣赏：这些几何图形中又体现了什么？1.继续欣赏：观察以下函数图象，从图象对称的角度把这些函数图象分类:函数的奇偶性美 丽 的 函 数 图 象观察下图，思考并讨论以下问题：（1）这两个函数图象有什么共同特征吗？（2）如何用数学语言来刻画这种特征呢？这两个函数的图象都关于y轴对称；相应的函数值对应表：发现： 当自变量取一对相反数时，相应的两个函数值相同.f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1)f(-3)=3=f(3) f(-2)=2=f(2) f(-1)=1=f(1)偶函数定义?猜想：f(-x)与f(x)的关系？奇函数定义： 如果对于函数f(x)的定义域内任意一个x都有f(-x)=-f(x)，那么函数f(x)就叫奇函数.偶函数定义： 如果对于函数f(x)的定义域内任意一个x都有f(-x)=f(x)，那么函数f(x)就叫偶函数.☆对奇函数、偶函数定义的说明:（1）由定义知，若x是定义域中的一个数值，则–x也必然在定义域
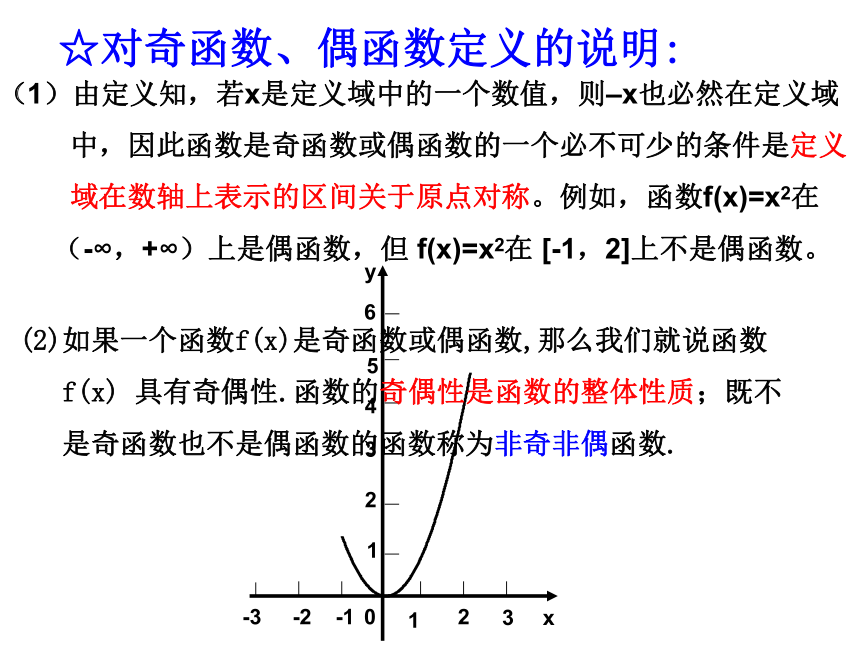
中，因此函数是奇函数或偶函数的一个必不可少的条件是定义
域在数轴上表示的区间关于原点对称。例如，函数f(x)=x2在
（-∞，+∞）上是偶函数，但 f(x)=x2在 [-1，2]上不是偶函数。(2)如果一个函数f(x)是奇函数或偶函数,那么我们就说函数
f(x) 具有奇偶性.函数的奇偶性是函数的整体性质；既不
是奇函数也不是偶函数的函数称为非奇非偶函数.例题选讲例1、判断下列函数的奇偶性:定义法奇函数奇函数偶函数非奇非偶函数判断函数奇偶性的步骤： (1)定义域是否关于原点对称？既奇又偶函数例1：判断下列函数的奇偶性：奇函数偶函数变式：已知f(x)是定义在R上的偶函数，且x≥0时，yxo1-1(1)求x<0时，f(x)的解析式.-33(2)求f(x)的单调区间与各区间上的单调性.题型 由奇偶性求函数解析式应用提高思考：函数f(x)的单调性与奇偶性有什么联系？变式：若f(x)是定义在R上的奇函数呢？ (1)若奇函数f(x)在[a，b]上是增函数, 那么该函
数在 [- b,- a]上是增函数还是减函数?
(2)若f(x)是偶函数又有怎样的情形呢? 奇函数单调性同,偶函数单调性反变式两个定义: 对于函数f(x)定义域内的任意一个x 1）用定义法判断函数奇偶性三个步骤:如果都有f(-x)=-f(x)，则f(x)为奇函数。
如果都有f(-x)= f(x)，则f(x)为偶函数。（1）先求出定义域，看定义域是否关于原点对称
（2）再判断f(-x)=-f(x)或f(-x)=f(x)是否成立。
（3）下结论课堂小结：判断函数奇偶性的两种方法：定义法与图像法。2）用图象法判断函数奇偶性：图象关于y轴对称的是偶函数，图象关于原点对称的是奇函数。函数的奇偶性（2）奇偶函数的性质：偶函数函数图象关于y轴对称奇函数函数图象关于原点成中心对称图象函数在对称区间上具有相同的单调性f(0)=0(即：若0在奇函数的定义域内，则此奇函数图象必过原点
如y=x)说明：奇偶函数图象的性质可用于：
a、简化函数图象的画法. b、判断函数的奇偶性练习.判断下列函数的奇偶性：课堂练习：例题选讲例2、已知f(x)为偶函数，g(x)为奇函数，将下图补充完整 .例2、已知函数y=f(x)是偶函数，它在y轴右边的图象如下图，画出在y轴左边的图象.解：画法略练习： P36 练习2例3（1）判断函数f(x)=x3+x 的奇偶性.因为对定义域内的每一个x，都有
f(-x)=(-x)3+（-x）=-(x3+x)=-f(x),解:对于函数f(x)= x3 +x,其定义域为（-∞，+∞）.所以，函数 f(x)=x3+x为奇函数。（2）如图，给出函数
f(x)=x3+x 图像的一部
分，你能根据f(x)的奇
偶性画出它在y轴左边
的图像吗？......用定义法判断或证明函数奇偶性的基本步骤：注意：若可以作出函数图象的，直接观察图象是否关于y轴对称或者关于原点对称。一求求定义域是否关于原点对称二找找关系f(x)与f(-x)三判断下结论奇或偶