2.1.1指数与指数幂的运算(一)(25张)
文档属性
| 名称 | 2.1.1指数与指数幂的运算(一)(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-09 00:00:00 | ||
图片预览








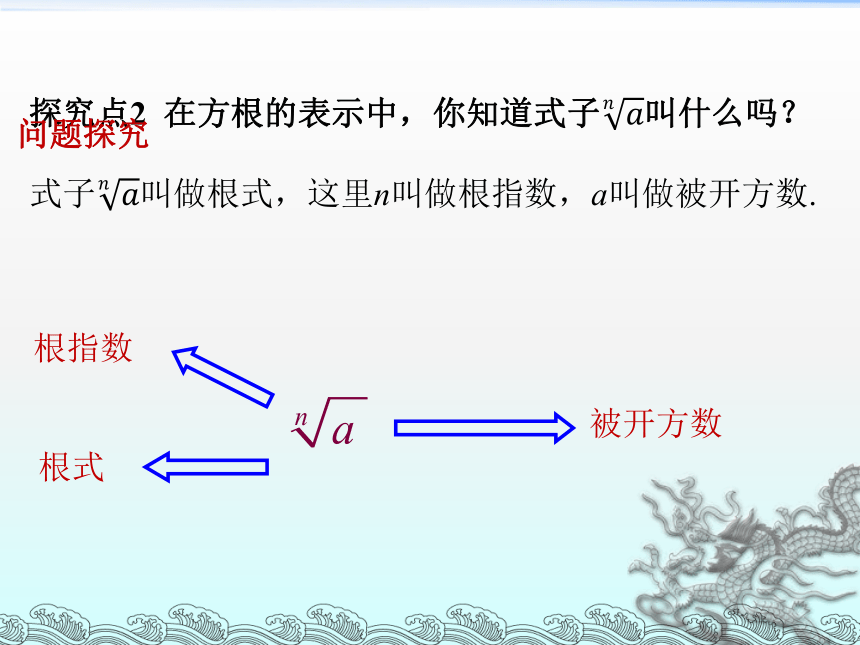
文档简介
课件25张PPT。2.1.1 指数与指数幂的运算(一)
第二章 §2.1 指数函数情境引入
关于根号的故事,最有价值和意义的当属它导致了第一次数学危机,并促使了逻辑学和几何学的发展.
公元前五世纪,古希腊有一个数学学派,名叫毕达哥拉斯学派,毕达哥拉斯学派提出的著名命题“万物皆数”是该学派的哲学基石.而“一切数均可表示成整数或整数之比”则是这一学派的数学信仰.学习目标:
1.理解n次方根、n次根式的概念.
2.正确运用根式运算性质化简、求值.
温 故 知 新 探究1:4次方根5次方根5次方根n次方根n次方根一、n次方根的定义:一般地,如果xn=a,那么x叫做a的n次方根,
(其中n>1,且n∈N*).探究2:二、n次方根的表示:1、当n为偶数时,正数a的n(偶)次方根有两个,互为相 反数正的记作 ,,负的记作
负数 无偶次方跟2、当n为奇数时,正数a的n奇次方根是一个正数,记
负数的n(奇)次方根是一个负数,记3、0的任何次方根都是0. 归 纳 总 结 用文字总结如下:??根指数 被开方数根式问题探究结论:探究点3 你能根据方根的意义确定下面式子的值吗?问题探究结论:an开奇次方根,则有结论:an开偶次方根,则有例2:求下列各式的值归纳总结:根式的运算性质?a |a| a -a 0 偶次 例1 化简:类型一 利用根式的性质化简或求值解答解答解 由题意知a-1≥0,即a≥1.
原式=a-1+|1-a|+1-a=a-1+a-1+1-a=a-1.小组讨论解答跟踪训练2 求下列各式的值:解答类型二 根式的意义解答∴a-1≥0,∴a≥1.当堂训练1.已知x5=6,则x等于√答案234512.m是实数,则下列式子中可能没有意义的是答案√234513.( )4运算的结果是
A.2 B.-2
C.±2 D.不确定答案√234514. 的值是
A.2 B.-2
C.±2 D.-8答案√234515.化简 (2x>1)的结果是
A.1-2x B.0
C.2x-1 D.(1-2x)2√答案234513.一个数到底有没有n次方根,我们一定先考虑被开方数到底是正数还是负数,还要分清n为奇数或偶数这两种情况.本课结束
第二章 §2.1 指数函数情境引入
关于根号的故事,最有价值和意义的当属它导致了第一次数学危机,并促使了逻辑学和几何学的发展.
公元前五世纪,古希腊有一个数学学派,名叫毕达哥拉斯学派,毕达哥拉斯学派提出的著名命题“万物皆数”是该学派的哲学基石.而“一切数均可表示成整数或整数之比”则是这一学派的数学信仰.学习目标:
1.理解n次方根、n次根式的概念.
2.正确运用根式运算性质化简、求值.
温 故 知 新 探究1:4次方根5次方根5次方根n次方根n次方根一、n次方根的定义:一般地,如果xn=a,那么x叫做a的n次方根,
(其中n>1,且n∈N*).探究2:二、n次方根的表示:1、当n为偶数时,正数a的n(偶)次方根有两个,互为相 反数正的记作 ,,负的记作
负数 无偶次方跟2、当n为奇数时,正数a的n奇次方根是一个正数,记
负数的n(奇)次方根是一个负数,记3、0的任何次方根都是0. 归 纳 总 结 用文字总结如下:??根指数 被开方数根式问题探究结论:探究点3 你能根据方根的意义确定下面式子的值吗?问题探究结论:an开奇次方根,则有结论:an开偶次方根,则有例2:求下列各式的值归纳总结:根式的运算性质?a |a| a -a 0 偶次 例1 化简:类型一 利用根式的性质化简或求值解答解答解 由题意知a-1≥0,即a≥1.
原式=a-1+|1-a|+1-a=a-1+a-1+1-a=a-1.小组讨论解答跟踪训练2 求下列各式的值:解答类型二 根式的意义解答∴a-1≥0,∴a≥1.当堂训练1.已知x5=6,则x等于√答案234512.m是实数,则下列式子中可能没有意义的是答案√234513.( )4运算的结果是
A.2 B.-2
C.±2 D.不确定答案√234514. 的值是
A.2 B.-2
C.±2 D.-8答案√234515.化简 (2x>1)的结果是
A.1-2x B.0
C.2x-1 D.(1-2x)2√答案234513.一个数到底有没有n次方根,我们一定先考虑被开方数到底是正数还是负数,还要分清n为奇数或偶数这两种情况.本课结束
