指数函数及其性质

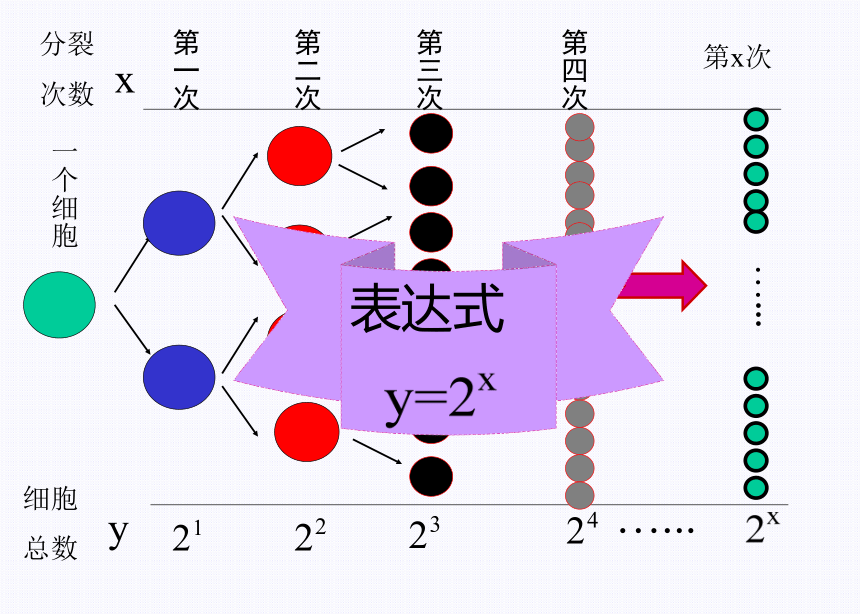
课件41张PPT。(必修1)第二章 基本初等函数(Ⅰ)2.1指数函数2.1.2 指数函数及其性质必修一 新课标人教A版某种细胞分裂时,第一次由1个分裂成2个，第2次由2个分裂成4个，如此下去，如果第x次分裂得到y个细胞，那么细胞个数y与分裂次数x的函数关系是什么？引例：1分裂
次数第一次第二次第三次第四次第x次…...x将一页白纸连续对折，（1）写出对折后的页（层）数y与对折次数x的关系式；（2）设这页纸的面积单位为1，则对折后每页纸的面积
s与对折次数x的关系又是 怎样的？解：对折次数 页数 每页面积 1 2 2 2×2=22 3 22 ×2=23… x 2x-1 ×2=2x x-1 2x-2 ×2=2x-1问题探究从两个实例中抽象出两个函数解析式这两个解析式有何共同特点?y与x之间是函数
关系吗？分析： 对于这两个关系式，每给自变量x的一个值，y都有唯一确定的值和它对应。
两个解析式都具有 的形式，其中自变量x是指数，底数a是一个大于0且不等于1的变量。
如果用字母a 来代替数1/2和2，那么以上两个函数都可以表示为：形如的 函数，其中自变量X是指数，底数a是一个大于0且不等于1的变量。
一、指数函数的概念注意 ：
（1）ax为一个整体，前面系数为1；
（2）a>0,且 a≠1 ;
（3）自变量x在幂指数的位置且为单个x； 概念剖析为何规定a?0，且a?1 ? 思考？
(3)若a=1时，函数值y=1，没有研究的必要. 概念剖析下列哪些是指数函数？想一想指数函数解析式的特点：动动手：
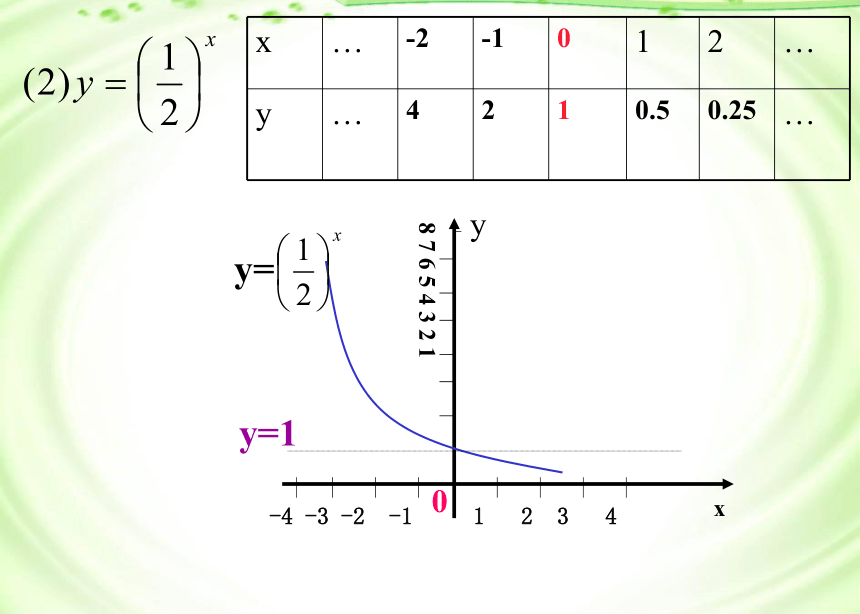
用描点法作出下列两组函数的图象，然后写出其一些性质：
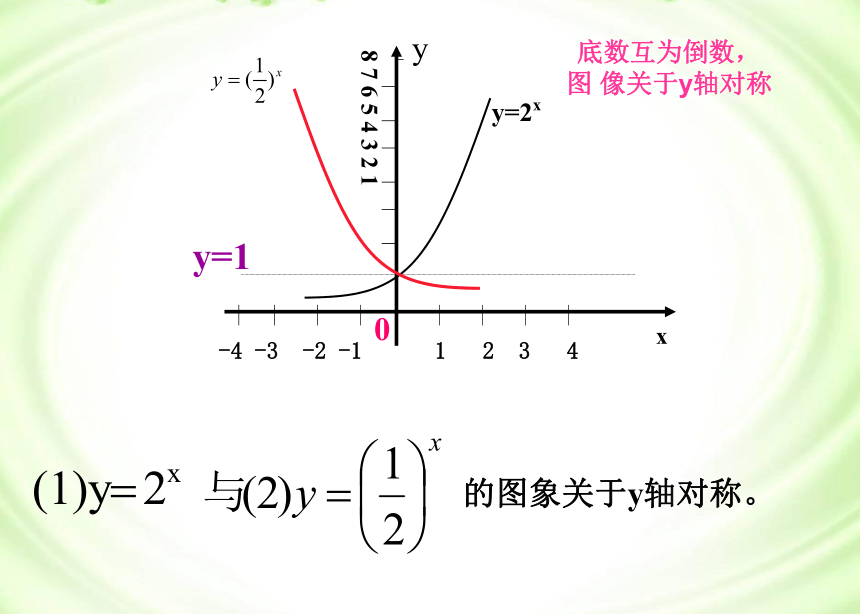
底数互为倒数，
图 像关于y轴对称二、图象和性质例1、用描点法作出下列两组函数的图象，然后写出其一些性质：
(1) y=2x 与 y=3x ; (a>1)

1、y=ax(a>0且a≠1)的代表图象及其一般性质分析(2) 与 y=(1/3)x . (0 的函数图像.试试看函 数 图 象 特 征 1函 数 图 象 特 征思考：若不用描点法，
这两个函数的图象又该
如何作出呢？关于y轴对称描点、连线a越大，曲线约往y轴靠近，且都过定点（0,1）a越来越大y1.如图是指数函数 ① y=ax ② y=bx
③ y=cx ④ y=dx 的图象，则 a,b,c,d 的大小关系（ ） .a b 1 c d
.b a 1 d c
.1 a b c d
.a b 1 d cBABCD①②③④巩固练习badc问题二：
　　图象的上升、下降与底数a有联系吗？问题三：
　　图象中有哪些特殊的点？答：四个图象都在第＿＿＿＿象限答：当底数＿＿时图象上升；当底数＿＿＿＿时图象下降．答：四个图象都经过点＿＿＿＿．Ⅰ、Ⅱ底数a由大变小时函数图像在第一象限内按＿＿＿＿ 时针方向旋转. 顺观察右边图象，回答下列问题： 图 象 性 质yx0y=1(0,1)y=ax
(a>1)yx(0,1)y=10y=ax
(010一和第二象限图像在x轴上方，和
x轴无限接近但是永
远不相交即 x = 0 时, y =a0=12.指数函数的图象和性质1.图象全在x轴上方，与x轴无限接近。1.定义域为R，值域为(0,+?).2.图象过定点（0，1）2.当x=0时，y=13.自左向右图象逐渐上升3.自左向右图象逐渐下降3.在R上是增函数3.在R上是减函数4.图象分布在左下和右上两个区域内4.图象分布在左上和右下两个区域内4.当x>0时,y>1;当x<0时,00时, 01.
左右无限上冲天，
永与横轴不沾边.
大 1 增，小 1 减，
图象恒过(0,1)点.口诀 2.若函数y=(a-1)x在R上为减函数，则a满足（ ）
0 < a < 1
a > 1
1< a < 2
a > 2 CBADC巩固练习解：例题分析练一练2.求下列函数的定义域1.函数是 指数函数，则 =________
5.函数 是减函数，求 的取值
范围.3｛x︱x≥2 ｝｛x︱x≠0｝(0,4)3x二、新 课例2、比较下列各组数的大小：解：①②、解：③、④、小结比较指数大小的方法：①、构造函数法：要点是利用函数的单调性，数的特征是同底不同指（包括可以化为同底的），若底数是参变量要注意分类讨论。②、搭桥比较法：用别的数如0或1做桥。数的特征是不同底不同指。指数函数单调性的应用比较两数的大小
②异底同指:构造函数法(多个),利用函数图象在y轴左右两侧的特点。比较指数幂大小的方法：①同底异指：构造函数法(一个), 利用函数的单调性,若底数是参变量要注意分类讨论。③异底异指:寻求中间量=a-x图象位置与底数关系a-x ⑴ 当底数a>1时，图象上升，且底数越大
　　时，图象向上越靠近于y轴。
⑵当底数0　　时，图象向右越靠近于x轴。结论2：课本第57页 例8列表： 由以上表格，可以方便地得到经过x年后，我国的人口数为：常用的指数增长模型：课堂小结指数函数y=ax(a>0且a≠1)的图象和性质(3)当a>1时，是增函数。

(3)自左向右看，a>1图象逐渐上升;(4)当a>1时，图象在第一象
限内的纵坐标都大于1;(2) y=a0=1 即x=0时y=1(2)这些图象都经过(0，1)点(1)x∈R, y=ax >0(1)这些图象都位于x轴上方函数性质图象特征当01 当0于1. (01．本节课学习了哪些知识?
3．如何记忆函数的性质?感悟收获,巩固拓展小结：数形结合的方法记忆2.记住两个基本图形4、指数函数概念； 5、指数比较大小的方法； ①、构造函数法：要点是利用函数的单调性，数的特征是同底不同指（包括可以化为同底的），若底数是参变量要注意分类讨论。②、搭桥比较法：用别的数如0或1做桥。数的特征是不同底不同指。 函数y = ax(a?0，且a ?1)叫做指数函数，其中x是自变量 .函数的定义域是R .课堂练习 P58 1~3 作业 P59 5,6,7感悟收获,巩固拓展课本P59 A组 5，6题课后作业再见！谢谢！点滴积累 丰富人生