12.2 三角形全等的判定同步课时作业(4)
文档属性
| 名称 | 12.2 三角形全等的判定同步课时作业(4) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-09 00:00:00 | ||
图片预览


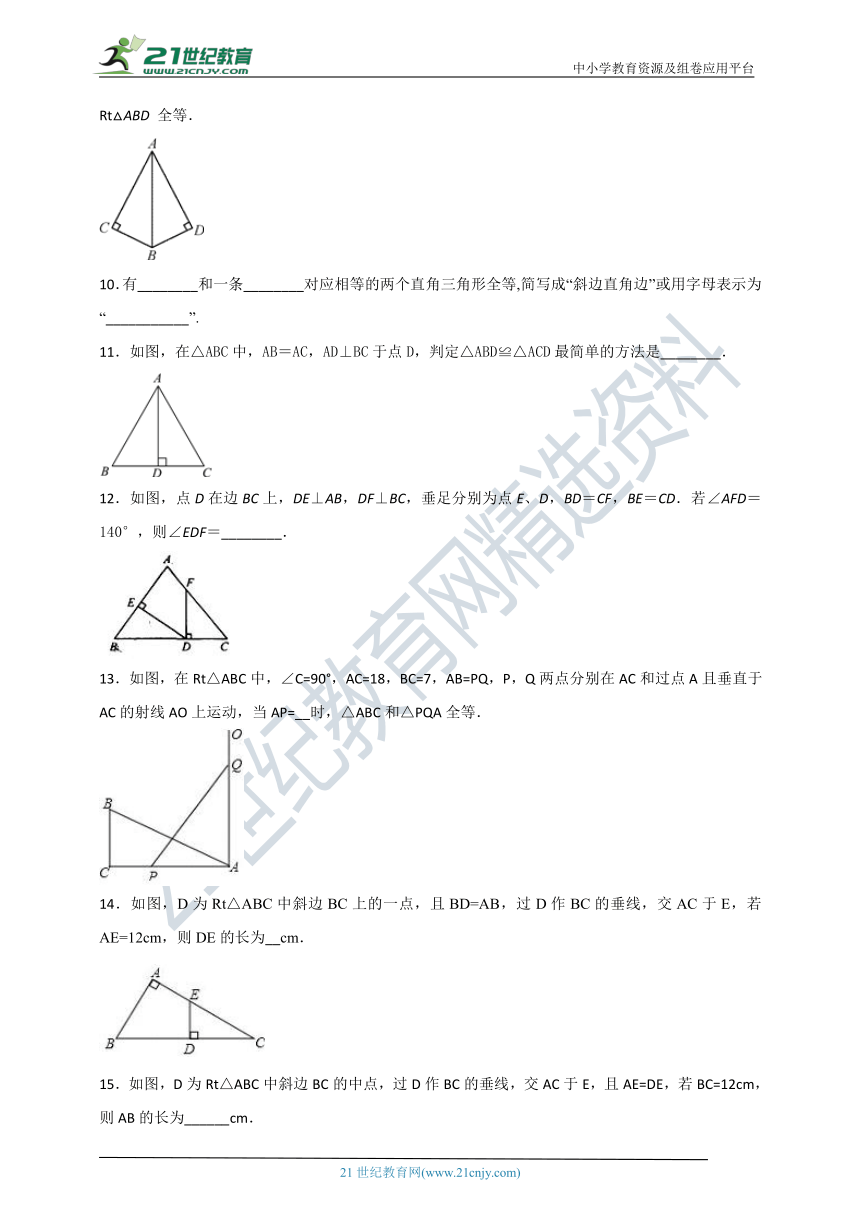
文档简介
12.2 三角形全等的判定同步课时作业(4)
姓名:___________班级:___________考号:___________
一、选择题
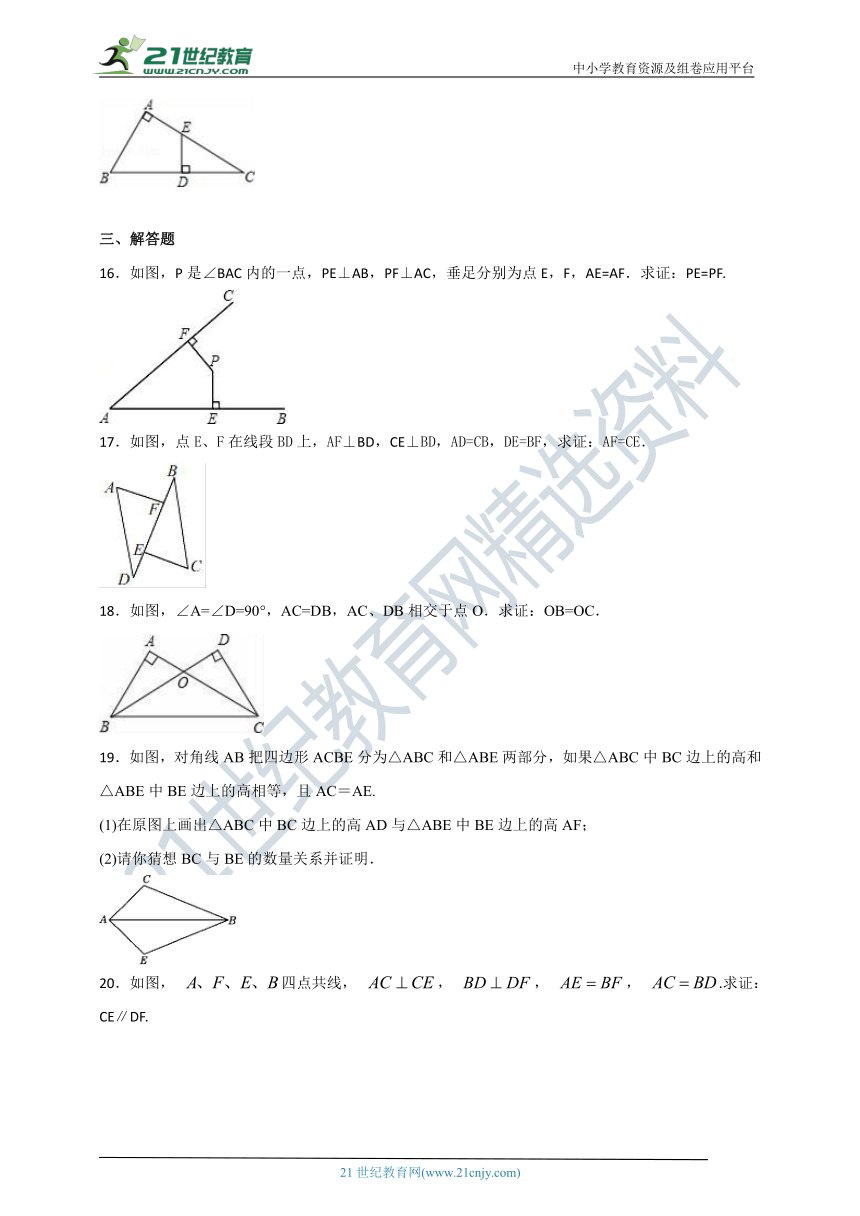
1.如图,点P是∠BAC内一点,且点P到AB,AC的距离相等,则△PEA≌△PFA的理由是( )
A. HL B. AAS C. SSS D. ASA
2.如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC,交AB于E,则下列结论一定正确的是( )
A. AE=BE B. DB=DE C. AE=BD D. ∠BCE=∠ACE
3.如图,在△ABC中,∠C=90°,DE⊥AB于点D,BC=BD.如果AC=3cm,那么AE+DE= ( )
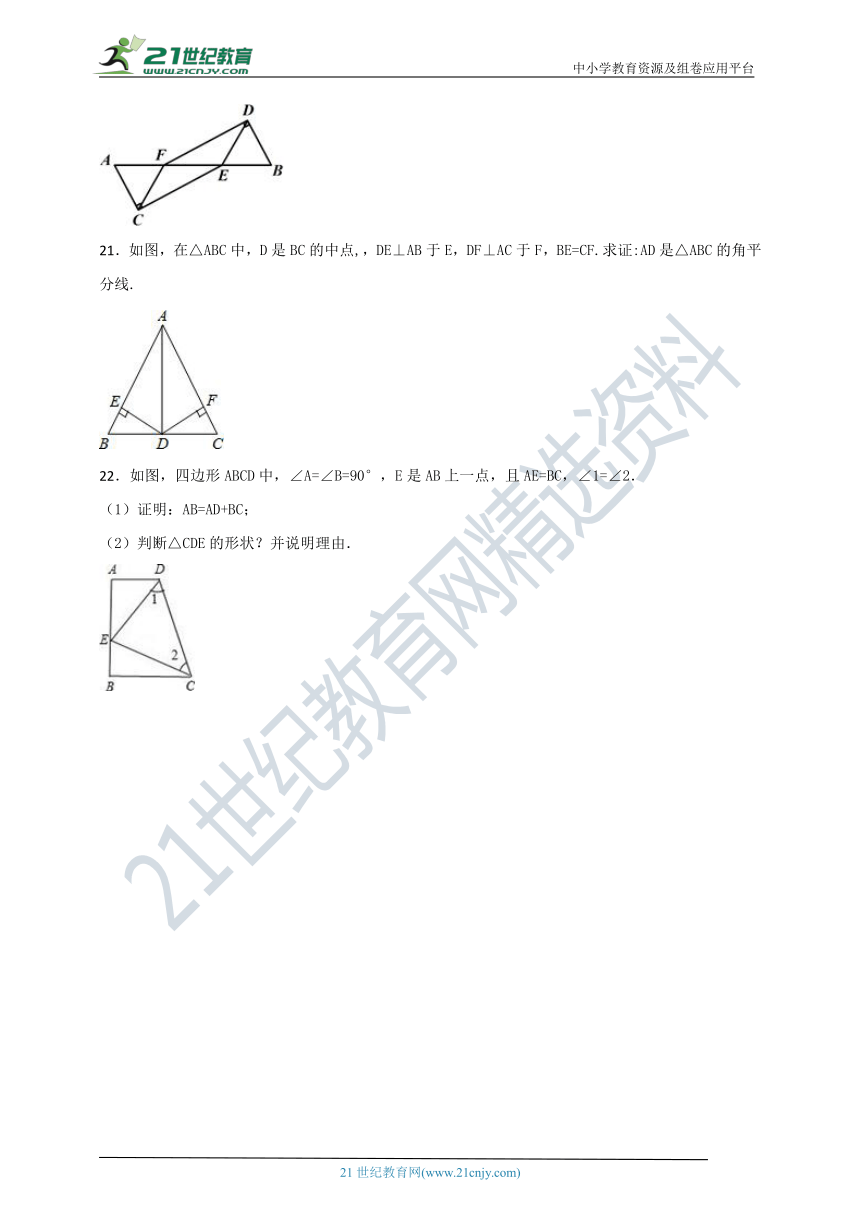
A. 2 cm B. 4 cm C. 3 cm D. 5 cm
4.如图6所示,在△ABC和△ABD中,∠C=∠D=90°,要利用“HL”判定△ABC≌△ABD成立,还需要添加的条件是( )
A. ∠BAC=∠BAD B. BC=BD或AC=AD C. ∠ABC=∠ABD D. AB为公共边
5.如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是( )
A. SAS B. ASA C. AAS D. HL
6.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
A. 40° B. 50° C. 60° D. 75°
7.已知,如图,B、C、E三点在同一条直线上,,,,则不正确的结论是( )
A. 与互为余角 B. C. D.
8.如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )
A. SAS B. SSS C. AAS D. HL
二、填空题
9.如图,∠C=∠D=90o,添加一个条件:______________ (写出一个条件即可),可使 Rt△ABC 与Rt△ABD 全等.
10.有________和一条________对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“___________”.
11.如图,在△ABC中,AB=AC,AD⊥BC于点D,判定△ABD≌△ACD最简单的方法是________.
12.如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E、D,BD=CF,BE=CD.若∠AFD=140°,则∠EDF=________.
13.如图,在Rt△ABC中,∠C=90°,AC=18,BC=7,AB=PQ,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=__时,△ABC和△PQA全等.
14.如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为__cm.
15.如图,D为Rt△ABC中斜边BC的中点,过D作BC的垂线,交AC于E,且AE=DE,若BC=12cm,则AB的长为______cm.
三、解答题
16.如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:PE=PF.
17.如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,求证:AF=CE.
18.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
19.如图,对角线AB把四边形ACBE分为△ABC和△ABE两部分,如果△ABC中BC边上的高和△ABE中BE边上的高相等,且AC=AE.
(1)在原图上画出△ABC中BC边上的高AD与△ABE中BE边上的高AF;
(2)请你猜想BC与BE的数量关系并证明.
20.如图, 四点共线, , , , .求证:CE∥DF.
21.如图,在△ABC中,D是BC的中点,,DE⊥AB于E,DF⊥AC于F,BE=CF.求证:AD是△ABC的角平分线.
22.如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
参考答案
1.A
【解析】试题分析:根据题意可得:PE=PF,AP=AP,∠AFP=∠AEP=90°,则我们可以根据HL定理得出三角形全等,故选A.
2.D
【解析】A中,∵DE⊥BC,∠A=90°,∴∠A=∠CDE=90°,
在Rt△CAE和Rt△CDE中,∵CA=CD,CE=CE,
∴Rt△CAE≌Rt△CDE(HL),
∴AE=DE,
∵在Rt△BED中,BE>DE,∴BE>AE,故A错误;
B中,根据已知不能得出BD=DE,故B错误;
C中,根据已知不能得出BD=DE,又由DE=AE,即不能推出BD=AE,故C错误;
D中,∵Rt△CAE≌Rt△CDE,∴∠BCE=∠ACE,故D正确.
故选D.
点睛:本题关键是证明直角三角形全等,直角三角形全等的判定定理有SAS,ASA,AAS,SSS,HL.
3.C
【解析】
【分析】
首先证明进而得到,再由即可得到答案.
【详解】
于,
,
在和中,
,
,
,
.
故选:.
【点睛】
此题主要考查了全等三角形的判定与性质,关键是掌握证明三角形全等的判定定理.
4.B
【解析】
【分析】
在两个直角三角形中,斜边和任意一条直角边分别对应相等,两直角三角形全等,即HL定理.
【详解】
需要添加的条件为BC=BD或AC=AD,理由为:
若添加的条件为BC=BD,
在Rt△ABC与Rt△ABD中,
∵?, ∴Rt△ABC≌Rt△ABD(HL),
若添加的条件为AC=AD,
在Rt△ABC与Rt△ABD中,
∵?,
?∴Rt△ABC≌Rt△ABD(HL),
故选B
【点睛】
本题主要考查全等三角形的判定定理,解决本题的关键是要熟练掌握全等三角形的判定定理.
5.D
【解析】∵在Rt△ABC与Rt△DEF中,,
∴Rt△ABC≌Rt△DEF(HL),
故选D.
6.B
【解析】
分析:本题要求∠2,先要证明Rt△ABC≌Rt△ADC(HL),则可求得∠2=∠ACB=90°-∠1的值.
详解:∵∠B=∠D=90°
在Rt△ABC和Rt△ADC中
,
∴Rt△ABC≌Rt△ADC(HL)
∴∠2=∠ACB=90°-∠1=50°.
故选:B.
点睛:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
7.D
【解析】
【分析】
先利用HL证明Rt△ABC≌Rt△CED(HL),根据全等三角形对应角相等可得∠A=∠2,∠1=∠D,继而可得∠A+∠D=90°,∠1+∠2=90°,由此对各选项进行判断即可.
【详解】
∵∠B=∠E=90°,
在Rt△ABC和Rt△CED中,
∴Rt△ABC≌Rt△CED(HL),故C正确,
∴∠A=∠2,∠1=∠D,
∵∠1+∠A=90°,
∴∠A+∠D=90°,∠1+∠2=90°,
∴∠A与∠D互为余角,故A、B正确;D 错误,
故选D.
【点睛】
本题考查了全等三角形的判定与性质,熟练掌握“HL”是解本题的关键.
8.D
【解析】试题解析:在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP是∠AOB的平分线.
故选D.
9.AC=AD 等(答案不唯一)
【解析】已知条件有:∠C=∠D=90°,AB=AB,
所以添加条件AC=AD可以根据HL判定Rt△ABC 与Rt△ABD 全等.
故答案为AC=AD.
点睛:掌握直角三角形全等的判定定理.
10.斜边,直角边,HL
【解析】
【分析】
根据全等直角三角形的判定定理填空.
【详解】
有斜边和一条直角边对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“HL”.
故答案为:(1). 斜边, (2). 直角边, (3). HL
【点睛】
本题考核知识点:全等直角三角形的判定. 解题关键点:熟记全等直角三角形的判定定理.
11.HL
【解析】
【分析】
求出∠ADB=∠ADC=90°,根据HL即可推出.
【详解】
HL,理由是:∵AD⊥BC, ∴∠ADB=∠ADC=90°, ∴在Rt△ADB和Rt△ADC中
∴Rt△ADB≌Rt△ADC(HL), 故答案为:HL.
【点睛】
本题考查了直角三角形全等的应用,注意:直角三角形全等的判定定理有SAS,ASA,AAS,SSS,HL.
12.50°
【解析】试题分析:根据∠AFD=140°可得:∠DFC=180°-140°=40°,根据BD=CF,BE=CD可以利用HL定理得出Rt△BED和Rt△CDF全等,则∠EDB=∠DFC=40°,则根据平角的性质可得:∠EDF=180°-90°-40°=50°.
13.7或18
【解析】当AP=7或18时,△ABC和△PQA全等,
理由是:∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
①当AP=7=BC时
在Rt△ACB和Rt△QAP中, ,
∴Rt△ACB≌Rt△QAP(HL),
②当AP=18=AC时,
在Rt△ACB和Rt△PAQ中,
,
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:7或18.
点睛:本题考查三角形全等的判定方法,判定两个三角形的全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能全等,根据已知结合图形及判定方法选择条件是正确解答本题的关键.
14.12
【解析】
连接BE,
∵D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,
∴∠A=∠BDE=90°,
∴在Rt△DBE和Rt△ABE中,
BD=AB(已知),BE=EB(公共边),
∴Rt△DBE≌Rt△ABE(HL),
∴AE=ED,
又∵AE=12cm,
∴ED=12cm.
故填12.
15.12.
【解析】根据已知条件,先证明Rt△DBE≌Rt△ABE,再根据全等三角形的性质(全等三角形的对应边相等)来求AB的长度.
解:连接BE.
∵D为Rt△ABC中斜边BC上的中点,且AE=DE,
∴∠A=∠BDE=90°, ∴在Rt△DBE和Rt△ABE中, BD=AB(已知),BE=EB(公共边), ∴Rt△DBE≌Rt△ABE(HL), ∴AB=BD, 又∵BC=12cm, ∴BD=6cm. 故填12.
16.见解析
【解析】试题分析:连接AP,证明Rt△APF≌Rt△APE,便可得PE=PF.
解:连接AP,
∵PE⊥AB,PF⊥AC,∴∠AEP=∠AFP=90°,
∵在Rt△AEP和Rt△AFP中,AP=AP,AE=AF,
∴Rt△AEP≌Rt△AFP(HL),
∴PE=PF.
17.证明见解析
【解析】
【分析】
首先证明BE=DF,然后依据HL可证明Rt△ADF≌Rt△CBE,从而可得到AF=CE.
【详解】
∵DE=BF,
∴DE+EF=BF+EF,即DF=BE,
在Rt△ADF和Rt△CBE中,,
∴Rt△ADF≌Rt△CBE(HL),
∴AF=CE.
【点睛】
本题考查了全等三角形的性质和判定,熟练掌握全等三角形的性质和判定定理是解题的关键.
18.证明见解析.
【解析】分析:因为∠A=∠D=90°,AC=BD,BC=BC,知Rt△BAC≌Rt△CDB(HL),所以∠ACB=∠DBC,故OB=OC.
【解答】证明:在Rt△ABC和Rt△DCB中
,
∴Rt△ABC≌Rt△DCB(HL),
∴∠OBC=∠OCB,
∴BO=CO.
点睛:此题主要考查了全等三角形的判定,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.
19.(1)见解析;(2)BC=BE.
【解析】
【分析】
(1)根据作三角形的高的方法,作出AD、AF;
(2)根据HL证明Rt△ACD≌Rt△AEF,从而得出CD=EF,再根据HL证明Rt△ABD≌Rt△ABF,从而得出BD=BF,再利用等式的性质得出:BD-CD=BF-EF,即BC=BE.
【详解】
解:(1)画出高AD,AF,如图所示.
(2)猜想:BC=BE.证明如下:
∵AD⊥BC,AF⊥BE,
∴△ACD,△AEF,△ABD,△ABF都是直角三角形.
在Rt△ACD和Rt△AEF中,
∴Rt△ACD≌Rt△AEF(HL).
∴CD=EF(全等三角形的对应边相等).
在Rt△ABD和Rt△ABF中,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF(全等三角形的对应边相等).
∴BD-CD=BF-EF(等式的性质),即BC=BE.
【点睛】
考查了全等三角形的判定和性质,解题关键是运用HL证明Rt△ACD≌Rt△AEF和Rt△ABD≌Rt△ABF得出CD=EF和BD=BF.
20.证明见解析.
【解析】试题分析:利用HL证明RtΔACE?RtΔBDF,根据全等三角形的性质即可得∠AEC=∠BFD,由内错角相等,两直线平行即可得CE∥DF.
试题解析:
∵AC⊥CE,BD⊥DF,
∴∠ACE=∠BDF=90°,
又∵AE=BF,AC=BD,
∴RtΔACE?RtΔBDF(HL),
∴∠AEC=∠BFD,
∴CE∥DF.
21.见解析
【解析】分析:由D为BC的中点,可得BD=DC,结合已知条件不难证明Rt△BED≌Rt△CFD;根据全等三角形的性质可得DE=DF,结合已知DE⊥AB,DF⊥AC即可证明结论.
详解:(1)∵DE⊥AB于E,DF⊥AC于F?
∴∠DEB=∠DFC=90°,
∵D是BC的中点,
∴BD=CD,
在Rt△BED和Rt△CFD中,?
BD=CD,BE=CF,
∴Rt△BED≌Rt△CFD(HL)?
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC.
点睛:本题考查了全等三角形的判定与性质,角平分线的判定,熟练掌握“HL”定理和角的内部到角两边距离相等的点在角的平分线上是解答本题的关键.
22.见解析
【解析】分析:(1)易证DE=CE,即可证明RT△ADE≌RT△BEC,可得AD=BE,即可解题; (2)由RT△ADE≌RT△BEC可得∠AED=∠BCE,即可求得∠DEC=90°,即可解题.
详解:(1)∵∠1=∠2,
∴DE=CE,
∵在RT△ADE和RT△BEC中,,
∴RT△ADE≌RT△BEC,(HL)
∴AD=BE,
∵AB=AE+BE,
∴AB=AD+BC;
(2)∵RT△ADE≌RT△BEC,
∴∠AED=∠BCE,
∵∠BCE+∠CEB=90°,
∴∠CEB+∠AED=90°,
∴∠DEC=90°,
∴△CDE为等腰直角三角形.
点睛:本题考查了等腰三角形的判定,垂直的定义,全等三角形的判定,全等三角形对应角、对应边相等的性质,本题中求证RT△ADE≌RT△BEC是解题的关键。
姓名:___________班级:___________考号:___________
一、选择题
1.如图,点P是∠BAC内一点,且点P到AB,AC的距离相等,则△PEA≌△PFA的理由是( )
A. HL B. AAS C. SSS D. ASA
2.如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC,交AB于E,则下列结论一定正确的是( )
A. AE=BE B. DB=DE C. AE=BD D. ∠BCE=∠ACE
3.如图,在△ABC中,∠C=90°,DE⊥AB于点D,BC=BD.如果AC=3cm,那么AE+DE= ( )
A. 2 cm B. 4 cm C. 3 cm D. 5 cm
4.如图6所示,在△ABC和△ABD中,∠C=∠D=90°,要利用“HL”判定△ABC≌△ABD成立,还需要添加的条件是( )
A. ∠BAC=∠BAD B. BC=BD或AC=AD C. ∠ABC=∠ABD D. AB为公共边
5.如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是( )
A. SAS B. ASA C. AAS D. HL
6.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
A. 40° B. 50° C. 60° D. 75°
7.已知,如图,B、C、E三点在同一条直线上,,,,则不正确的结论是( )
A. 与互为余角 B. C. D.
8.如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )
A. SAS B. SSS C. AAS D. HL
二、填空题
9.如图,∠C=∠D=90o,添加一个条件:______________ (写出一个条件即可),可使 Rt△ABC 与Rt△ABD 全等.
10.有________和一条________对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“___________”.
11.如图,在△ABC中,AB=AC,AD⊥BC于点D,判定△ABD≌△ACD最简单的方法是________.
12.如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E、D,BD=CF,BE=CD.若∠AFD=140°,则∠EDF=________.
13.如图,在Rt△ABC中,∠C=90°,AC=18,BC=7,AB=PQ,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=__时,△ABC和△PQA全等.
14.如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为__cm.
15.如图,D为Rt△ABC中斜边BC的中点,过D作BC的垂线,交AC于E,且AE=DE,若BC=12cm,则AB的长为______cm.
三、解答题
16.如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:PE=PF.
17.如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,求证:AF=CE.
18.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
19.如图,对角线AB把四边形ACBE分为△ABC和△ABE两部分,如果△ABC中BC边上的高和△ABE中BE边上的高相等,且AC=AE.
(1)在原图上画出△ABC中BC边上的高AD与△ABE中BE边上的高AF;
(2)请你猜想BC与BE的数量关系并证明.
20.如图, 四点共线, , , , .求证:CE∥DF.
21.如图,在△ABC中,D是BC的中点,,DE⊥AB于E,DF⊥AC于F,BE=CF.求证:AD是△ABC的角平分线.
22.如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
参考答案
1.A
【解析】试题分析:根据题意可得:PE=PF,AP=AP,∠AFP=∠AEP=90°,则我们可以根据HL定理得出三角形全等,故选A.
2.D
【解析】A中,∵DE⊥BC,∠A=90°,∴∠A=∠CDE=90°,
在Rt△CAE和Rt△CDE中,∵CA=CD,CE=CE,
∴Rt△CAE≌Rt△CDE(HL),
∴AE=DE,
∵在Rt△BED中,BE>DE,∴BE>AE,故A错误;
B中,根据已知不能得出BD=DE,故B错误;
C中,根据已知不能得出BD=DE,又由DE=AE,即不能推出BD=AE,故C错误;
D中,∵Rt△CAE≌Rt△CDE,∴∠BCE=∠ACE,故D正确.
故选D.
点睛:本题关键是证明直角三角形全等,直角三角形全等的判定定理有SAS,ASA,AAS,SSS,HL.
3.C
【解析】
【分析】
首先证明进而得到,再由即可得到答案.
【详解】
于,
,
在和中,
,
,
,
.
故选:.
【点睛】
此题主要考查了全等三角形的判定与性质,关键是掌握证明三角形全等的判定定理.
4.B
【解析】
【分析】
在两个直角三角形中,斜边和任意一条直角边分别对应相等,两直角三角形全等,即HL定理.
【详解】
需要添加的条件为BC=BD或AC=AD,理由为:
若添加的条件为BC=BD,
在Rt△ABC与Rt△ABD中,
∵?, ∴Rt△ABC≌Rt△ABD(HL),
若添加的条件为AC=AD,
在Rt△ABC与Rt△ABD中,
∵?,
?∴Rt△ABC≌Rt△ABD(HL),
故选B
【点睛】
本题主要考查全等三角形的判定定理,解决本题的关键是要熟练掌握全等三角形的判定定理.
5.D
【解析】∵在Rt△ABC与Rt△DEF中,,
∴Rt△ABC≌Rt△DEF(HL),
故选D.
6.B
【解析】
分析:本题要求∠2,先要证明Rt△ABC≌Rt△ADC(HL),则可求得∠2=∠ACB=90°-∠1的值.
详解:∵∠B=∠D=90°
在Rt△ABC和Rt△ADC中
,
∴Rt△ABC≌Rt△ADC(HL)
∴∠2=∠ACB=90°-∠1=50°.
故选:B.
点睛:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
7.D
【解析】
【分析】
先利用HL证明Rt△ABC≌Rt△CED(HL),根据全等三角形对应角相等可得∠A=∠2,∠1=∠D,继而可得∠A+∠D=90°,∠1+∠2=90°,由此对各选项进行判断即可.
【详解】
∵∠B=∠E=90°,
在Rt△ABC和Rt△CED中,
∴Rt△ABC≌Rt△CED(HL),故C正确,
∴∠A=∠2,∠1=∠D,
∵∠1+∠A=90°,
∴∠A+∠D=90°,∠1+∠2=90°,
∴∠A与∠D互为余角,故A、B正确;D 错误,
故选D.
【点睛】
本题考查了全等三角形的判定与性质,熟练掌握“HL”是解本题的关键.
8.D
【解析】试题解析:在Rt△OMP和Rt△ONP中,
,
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP=∠NOP,
∴OP是∠AOB的平分线.
故选D.
9.AC=AD 等(答案不唯一)
【解析】已知条件有:∠C=∠D=90°,AB=AB,
所以添加条件AC=AD可以根据HL判定Rt△ABC 与Rt△ABD 全等.
故答案为AC=AD.
点睛:掌握直角三角形全等的判定定理.
10.斜边,直角边,HL
【解析】
【分析】
根据全等直角三角形的判定定理填空.
【详解】
有斜边和一条直角边对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“HL”.
故答案为:(1). 斜边, (2). 直角边, (3). HL
【点睛】
本题考核知识点:全等直角三角形的判定. 解题关键点:熟记全等直角三角形的判定定理.
11.HL
【解析】
【分析】
求出∠ADB=∠ADC=90°,根据HL即可推出.
【详解】
HL,理由是:∵AD⊥BC, ∴∠ADB=∠ADC=90°, ∴在Rt△ADB和Rt△ADC中
∴Rt△ADB≌Rt△ADC(HL), 故答案为:HL.
【点睛】
本题考查了直角三角形全等的应用,注意:直角三角形全等的判定定理有SAS,ASA,AAS,SSS,HL.
12.50°
【解析】试题分析:根据∠AFD=140°可得:∠DFC=180°-140°=40°,根据BD=CF,BE=CD可以利用HL定理得出Rt△BED和Rt△CDF全等,则∠EDB=∠DFC=40°,则根据平角的性质可得:∠EDF=180°-90°-40°=50°.
13.7或18
【解析】当AP=7或18时,△ABC和△PQA全等,
理由是:∵∠C=90°,AO⊥AC,
∴∠C=∠QAP=90°,
①当AP=7=BC时
在Rt△ACB和Rt△QAP中, ,
∴Rt△ACB≌Rt△QAP(HL),
②当AP=18=AC时,
在Rt△ACB和Rt△PAQ中,
,
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:7或18.
点睛:本题考查三角形全等的判定方法,判定两个三角形的全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能全等,根据已知结合图形及判定方法选择条件是正确解答本题的关键.
14.12
【解析】
连接BE,
∵D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,
∴∠A=∠BDE=90°,
∴在Rt△DBE和Rt△ABE中,
BD=AB(已知),BE=EB(公共边),
∴Rt△DBE≌Rt△ABE(HL),
∴AE=ED,
又∵AE=12cm,
∴ED=12cm.
故填12.
15.12.
【解析】根据已知条件,先证明Rt△DBE≌Rt△ABE,再根据全等三角形的性质(全等三角形的对应边相等)来求AB的长度.
解:连接BE.
∵D为Rt△ABC中斜边BC上的中点,且AE=DE,
∴∠A=∠BDE=90°, ∴在Rt△DBE和Rt△ABE中, BD=AB(已知),BE=EB(公共边), ∴Rt△DBE≌Rt△ABE(HL), ∴AB=BD, 又∵BC=12cm, ∴BD=6cm. 故填12.
16.见解析
【解析】试题分析:连接AP,证明Rt△APF≌Rt△APE,便可得PE=PF.
解:连接AP,
∵PE⊥AB,PF⊥AC,∴∠AEP=∠AFP=90°,
∵在Rt△AEP和Rt△AFP中,AP=AP,AE=AF,
∴Rt△AEP≌Rt△AFP(HL),
∴PE=PF.
17.证明见解析
【解析】
【分析】
首先证明BE=DF,然后依据HL可证明Rt△ADF≌Rt△CBE,从而可得到AF=CE.
【详解】
∵DE=BF,
∴DE+EF=BF+EF,即DF=BE,
在Rt△ADF和Rt△CBE中,,
∴Rt△ADF≌Rt△CBE(HL),
∴AF=CE.
【点睛】
本题考查了全等三角形的性质和判定,熟练掌握全等三角形的性质和判定定理是解题的关键.
18.证明见解析.
【解析】分析:因为∠A=∠D=90°,AC=BD,BC=BC,知Rt△BAC≌Rt△CDB(HL),所以∠ACB=∠DBC,故OB=OC.
【解答】证明:在Rt△ABC和Rt△DCB中
,
∴Rt△ABC≌Rt△DCB(HL),
∴∠OBC=∠OCB,
∴BO=CO.
点睛:此题主要考查了全等三角形的判定,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.
19.(1)见解析;(2)BC=BE.
【解析】
【分析】
(1)根据作三角形的高的方法,作出AD、AF;
(2)根据HL证明Rt△ACD≌Rt△AEF,从而得出CD=EF,再根据HL证明Rt△ABD≌Rt△ABF,从而得出BD=BF,再利用等式的性质得出:BD-CD=BF-EF,即BC=BE.
【详解】
解:(1)画出高AD,AF,如图所示.
(2)猜想:BC=BE.证明如下:
∵AD⊥BC,AF⊥BE,
∴△ACD,△AEF,△ABD,△ABF都是直角三角形.
在Rt△ACD和Rt△AEF中,
∴Rt△ACD≌Rt△AEF(HL).
∴CD=EF(全等三角形的对应边相等).
在Rt△ABD和Rt△ABF中,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF(全等三角形的对应边相等).
∴BD-CD=BF-EF(等式的性质),即BC=BE.
【点睛】
考查了全等三角形的判定和性质,解题关键是运用HL证明Rt△ACD≌Rt△AEF和Rt△ABD≌Rt△ABF得出CD=EF和BD=BF.
20.证明见解析.
【解析】试题分析:利用HL证明RtΔACE?RtΔBDF,根据全等三角形的性质即可得∠AEC=∠BFD,由内错角相等,两直线平行即可得CE∥DF.
试题解析:
∵AC⊥CE,BD⊥DF,
∴∠ACE=∠BDF=90°,
又∵AE=BF,AC=BD,
∴RtΔACE?RtΔBDF(HL),
∴∠AEC=∠BFD,
∴CE∥DF.
21.见解析
【解析】分析:由D为BC的中点,可得BD=DC,结合已知条件不难证明Rt△BED≌Rt△CFD;根据全等三角形的性质可得DE=DF,结合已知DE⊥AB,DF⊥AC即可证明结论.
详解:(1)∵DE⊥AB于E,DF⊥AC于F?
∴∠DEB=∠DFC=90°,
∵D是BC的中点,
∴BD=CD,
在Rt△BED和Rt△CFD中,?
BD=CD,BE=CF,
∴Rt△BED≌Rt△CFD(HL)?
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC.
点睛:本题考查了全等三角形的判定与性质,角平分线的判定,熟练掌握“HL”定理和角的内部到角两边距离相等的点在角的平分线上是解答本题的关键.
22.见解析
【解析】分析:(1)易证DE=CE,即可证明RT△ADE≌RT△BEC,可得AD=BE,即可解题; (2)由RT△ADE≌RT△BEC可得∠AED=∠BCE,即可求得∠DEC=90°,即可解题.
详解:(1)∵∠1=∠2,
∴DE=CE,
∵在RT△ADE和RT△BEC中,,
∴RT△ADE≌RT△BEC,(HL)
∴AD=BE,
∵AB=AE+BE,
∴AB=AD+BC;
(2)∵RT△ADE≌RT△BEC,
∴∠AED=∠BCE,
∵∠BCE+∠CEB=90°,
∴∠CEB+∠AED=90°,
∴∠DEC=90°,
∴△CDE为等腰直角三角形.
点睛:本题考查了等腰三角形的判定,垂直的定义,全等三角形的判定,全等三角形对应角、对应边相等的性质,本题中求证RT△ADE≌RT△BEC是解题的关键。
