2018年秋新课堂高中数学人教A版选修1-1练习:专题强化训练3
文档属性
| 名称 | 2018年秋新课堂高中数学人教A版选修1-1练习:专题强化训练3 |

|
|
| 格式 | zip | ||
| 文件大小 | 97.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-10 00:00:00 | ||
图片预览


文档简介
专题强化训练(三)
(建议用时:45分钟)
[基础达标练]
1.一物体作直线运动,位移s(单位:m)与时间t(单位:s)之间的函数关系为s(t)=-2t2+8t,则这一物体在t=1 s时的加速度为 ( )
A.4 m/s2 B.-4 m/s2
C.6 m/s2 D.-6 m/s2
B [由导数的概念可求得速度v(单位:m/s)与时间t(单位:s)的函数关系为v(t)=-4t+8,它在t=1时的导数就是这一物体在t=1时的加速度a,所以a=v′(1),又v′(t)=-4,所以a=-4.]
2.函数f(x)=x3+ax2+bx+c,其中a,b,c为实数,当a2-3b<0时,f(x)在R上 ( )
A.是增函数 B.是减函数
C.是常函数 D.既不是增函数也不是减函数
A [f′(x)=3x2+2ax+b,方程3x2+2ax+b=0的判别式Δ=(2a)2-4×3b=4(a2-3b).因为a2-3b<0,所以Δ=4(a2-3b)<0,所以f′(x)在R上恒大于0,故f(x)在R上是增函数.]
3.函数f(x)=x2-ln x的极值点为( )
A.0,1,-1 B.
C.- D.,-
B [f(x)的定义域为(0,+∞),f′(x)=3x-=.
令f′(x)=0得x=或x=-(舍去),
当x>时,f′(x)>0,当0所以当x=时,f(x)取得极小值,从而f(x)的极小值点为x=,无极大值点.]
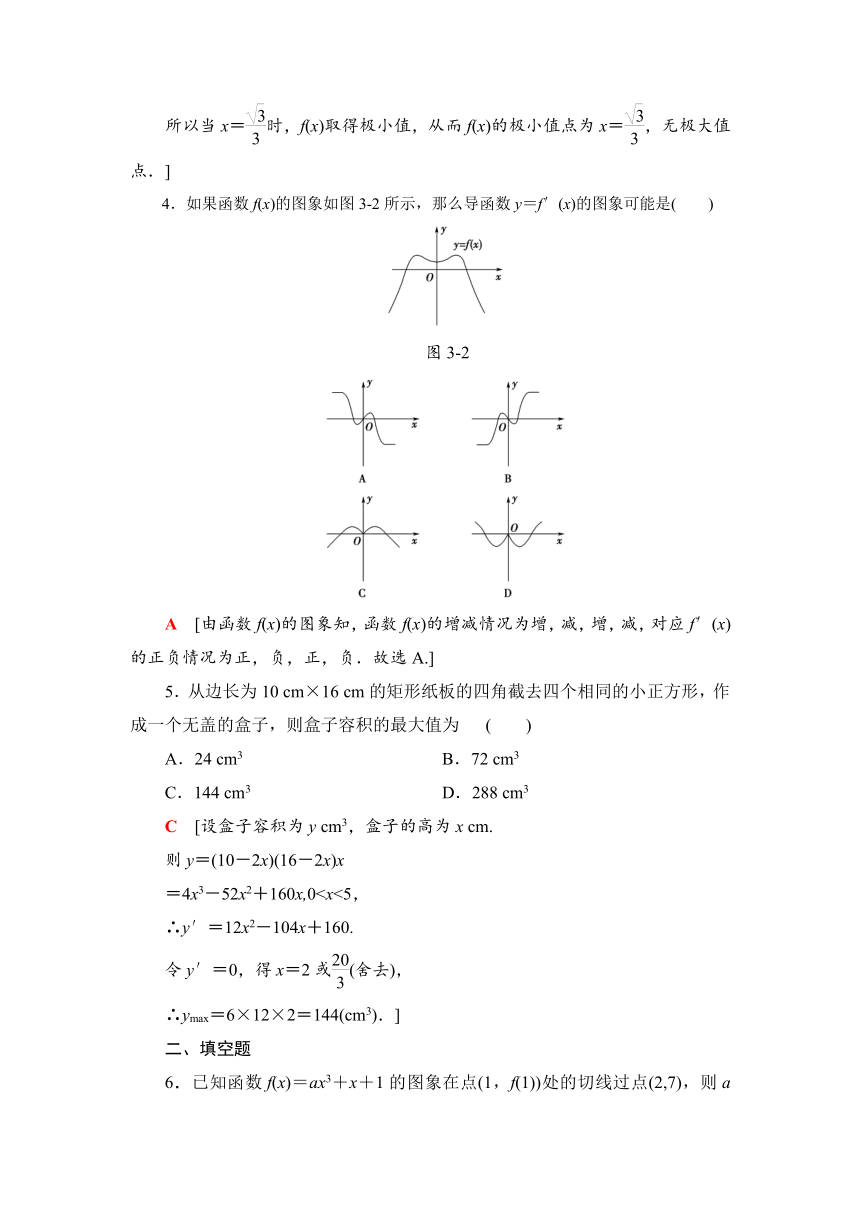
4.如果函数f(x)的图象如图3-2所示,那么导函数y=f′(x)的图象可能是( )
图3-2
A [由函数f(x)的图象知,函数f(x)的增减情况为增,减,增,减,对应f′(x)的正负情况为正,负,正,负.故选A.]
5.从边长为10 cm×16 cm的矩形纸板的四角截去四个相同的小正方形,作成一个无盖的盒子,则盒子容积的最大值为 ( )
A.24 cm3 B.72 cm3
C.144 cm3 D.288 cm3
C [设盒子容积为y cm3,盒子的高为x cm.
则y=(10-2x)(16-2x)x
=4x3-52x2+160x,0∴y′=12x2-104x+160.
令y′=0,得x=2或(舍去),
∴ymax=6×12×2=144(cm3).]
二、填空题
6.已知函数f(x)=ax3+x+1的图象在点(1,f(1))处的切线过点(2,7),则a=________.
1 [∵f′(x)=3ax2+1,
∴f′(1)=3a+1.
又f(1)=a+2,
∴切线方程为y-(a+2)=(3a+1)(x-1).
∵切线过点(2,7),∴7-(a+2)=3a+1,解得a=1.]
7.函数f(x)=(x≥2)的最大值为________.
2 [∵f(x)=,∴f′(x)==<0,∴函数f(x)在[2,+∞)上单调递减,故当x=2时,函数f(x)=取得最大值2.]
8.若函数f(x)=(mx-1)ex在(0,+∞)上单调递增,则实数m的取值范围是__________.
[1,+∞) [f′(x)=mex+(mx-1)ex=(mx+m-1)ex,
由题意知,f′(x)≥0在x∈[0,+∞)上恒成立.
也就是mx+m-1≥0在x∈[0,+∞)上恒成立,
当m≤0时显然不成立,
当m>0时,令g(x)=mx+m-1,
只需g(0)≥0,得m≥1.
即实数m的取值范围为[1,+∞).
三、解答题
9.已知函数g(x)=1-.
(1)求g(x)的单调区间;
(2)当[解] (1)因为g(x)=1-,
所以g′(x)=-=.
令g′(x)>0,得x>1;
令g′(x)<0,得0所以g(x)的单调递增区间是(1,+∞),单调递减区间是(0,1).
(2)证明:由(1)知g(x)=1-在(0,1)上单调递减,
所以当g(y),
即1->1-,
所以<,即<.
10.如图3-3,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r(r>0),计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,设CD=2x,梯形面积为S.
图3-3
(1)求面积S以x为自变量的函数关系式,并写出其定义域;
(2)求面积S的最大值.
[解] (1)依题意,设AB的中点为O,以O为原点建立平面直角坐标系xOy,如图所示,
设C的坐标为(x,y),则x,y满足方程+=1(y>0),
解得y=2(0所以S=(2x+2r)·2=2(x+r),其定义域为(0,r).
(2)由(1)可得S=.
记f(x)=4(x+r)2(r2-x2),0则f′(x)=8(x+r)2(r-2x).
令f′(x)=0,得x=.
当00;当所以f是f(x)的最大值.
因此,当x=时,S也取得最大值,最大值为=r2,
即等腰梯形的面积S的最大值为r2.
[能力提升练]
1.函数y=2x2-e|x|在[-2,2]的图象大致为( )
D [∵f(x)=2x2-e|x|,x∈[-2,2]是偶函数,又f(2)=8-e2∈(0,1),故排除A,B.设g(x)=2x2-ex,则g′(x)=4x-ex.又g′(0)<0,g′(2)>0,∴g(x)在(0,2)内至少存在一个极值点,∴f(x)=2x2-e|x|在(0,2)内至少存在一个极值点,排除C.故选D.]
2.已知函数f(x)=ax4-4ax3+b(a>0),x∈[1,4],f(x)的最大值为3,最小值为-6,则a+b=( )
A. B. C. D.
C [f′(x)=4ax3-12ax2.令f′(x)=0,得x=3或x=0(舍去).当1≤x<3时,f′(x)<0,当30,故x=3为极小值点,也是最小值点.∵f(3)=b-27a,f(1)=b-3a,f(4)=b,∴f(x)的最小值为f(3)=b-27a,最大值为f(4)=b,∴,解得,∴a+b=.]
3.函数y=xex在其极值点处的切线方程为__________.
y=- [由题知y′=ex+xex,令y′=0,解得x=-1,代入函数解析式可得极值点的坐标为,又极值点处的切线为平行于x轴的直线,故方程为y=-.]
4.若函数f(x)=2x2-ln x在定义域内的一个子区间(k-1,k+1)上不是单调函数,则实数k的取值范围是__________.
[由题意可知函数f(x)的定义域为(0,+∞),f′(x)=4x-=.由f′(x)>0,得函数f(x)的单调增区间为;由f′(x)<0,得函数f(x)的单调减区间为.由于函数f(x)在区间(k-1,k+1)上不是单调函数,所以k-1<5.已知函数f(x)=aln x(a>0).
(1)若曲线y=f(x)在点A(2,f(2))处的切线斜率为2,求实数a的值;
(2)当x>0时,求证:f(x)≥a;
(3)若在区间(1,e)上,>1恒成立,求实数a的取值范围.
[解] (1)∵f′(x)=,∴f′(2)==2,∴a=4.
(2)证明:令g(x)=f(x)-a,则g(x)=aln x-1+,
g′(x)=a.
令g′(x)>0,即a>0,解得x>1,
令g′(x)<0,即a<0,解得x<1,又x>0,∴0∴g(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
∴g(x)的最小值为g(1)=0,∴f(x)≥a.
(3)令h(x)=aln x+1-x,则h′(x)=-1,
令h′(x)>0,解得xa.
当a≥e时,h(x)在(1,e)上是增函数,∴h(x)>h(1)=0;
当1∴只需h(e)≥0,即a≥e-1;
当a≤1时,h(x)在(1,e)上单调递减,则只需h(e)≥0,
又h(e)=a+1-e<0,∴此时a不存在.
综上,实数a的取值范围为[e-1,+∞).
(建议用时:45分钟)
[基础达标练]
1.一物体作直线运动,位移s(单位:m)与时间t(单位:s)之间的函数关系为s(t)=-2t2+8t,则这一物体在t=1 s时的加速度为 ( )
A.4 m/s2 B.-4 m/s2
C.6 m/s2 D.-6 m/s2
B [由导数的概念可求得速度v(单位:m/s)与时间t(单位:s)的函数关系为v(t)=-4t+8,它在t=1时的导数就是这一物体在t=1时的加速度a,所以a=v′(1),又v′(t)=-4,所以a=-4.]
2.函数f(x)=x3+ax2+bx+c,其中a,b,c为实数,当a2-3b<0时,f(x)在R上 ( )
A.是增函数 B.是减函数
C.是常函数 D.既不是增函数也不是减函数
A [f′(x)=3x2+2ax+b,方程3x2+2ax+b=0的判别式Δ=(2a)2-4×3b=4(a2-3b).因为a2-3b<0,所以Δ=4(a2-3b)<0,所以f′(x)在R上恒大于0,故f(x)在R上是增函数.]
3.函数f(x)=x2-ln x的极值点为( )
A.0,1,-1 B.
C.- D.,-
B [f(x)的定义域为(0,+∞),f′(x)=3x-=.
令f′(x)=0得x=或x=-(舍去),
当x>时,f′(x)>0,当0
4.如果函数f(x)的图象如图3-2所示,那么导函数y=f′(x)的图象可能是( )
图3-2
A [由函数f(x)的图象知,函数f(x)的增减情况为增,减,增,减,对应f′(x)的正负情况为正,负,正,负.故选A.]
5.从边长为10 cm×16 cm的矩形纸板的四角截去四个相同的小正方形,作成一个无盖的盒子,则盒子容积的最大值为 ( )
A.24 cm3 B.72 cm3
C.144 cm3 D.288 cm3
C [设盒子容积为y cm3,盒子的高为x cm.
则y=(10-2x)(16-2x)x
=4x3-52x2+160x,0
令y′=0,得x=2或(舍去),
∴ymax=6×12×2=144(cm3).]
二、填空题
6.已知函数f(x)=ax3+x+1的图象在点(1,f(1))处的切线过点(2,7),则a=________.
1 [∵f′(x)=3ax2+1,
∴f′(1)=3a+1.
又f(1)=a+2,
∴切线方程为y-(a+2)=(3a+1)(x-1).
∵切线过点(2,7),∴7-(a+2)=3a+1,解得a=1.]
7.函数f(x)=(x≥2)的最大值为________.
2 [∵f(x)=,∴f′(x)==<0,∴函数f(x)在[2,+∞)上单调递减,故当x=2时,函数f(x)=取得最大值2.]
8.若函数f(x)=(mx-1)ex在(0,+∞)上单调递增,则实数m的取值范围是__________.
[1,+∞) [f′(x)=mex+(mx-1)ex=(mx+m-1)ex,
由题意知,f′(x)≥0在x∈[0,+∞)上恒成立.
也就是mx+m-1≥0在x∈[0,+∞)上恒成立,
当m≤0时显然不成立,
当m>0时,令g(x)=mx+m-1,
只需g(0)≥0,得m≥1.
即实数m的取值范围为[1,+∞).
三、解答题
9.已知函数g(x)=1-.
(1)求g(x)的单调区间;
(2)当
所以g′(x)=-=.
令g′(x)>0,得x>1;
令g′(x)<0,得0
(2)证明:由(1)知g(x)=1-在(0,1)上单调递减,
所以当
即1->1-,
所以<,即<.
10.如图3-3,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r(r>0),计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,设CD=2x,梯形面积为S.
图3-3
(1)求面积S以x为自变量的函数关系式,并写出其定义域;
(2)求面积S的最大值.
[解] (1)依题意,设AB的中点为O,以O为原点建立平面直角坐标系xOy,如图所示,
设C的坐标为(x,y),则x,y满足方程+=1(y>0),
解得y=2(0
(2)由(1)可得S=.
记f(x)=4(x+r)2(r2-x2),0
令f′(x)=0,得x=.
当0
因此,当x=时,S也取得最大值,最大值为=r2,
即等腰梯形的面积S的最大值为r2.
[能力提升练]
1.函数y=2x2-e|x|在[-2,2]的图象大致为( )
D [∵f(x)=2x2-e|x|,x∈[-2,2]是偶函数,又f(2)=8-e2∈(0,1),故排除A,B.设g(x)=2x2-ex,则g′(x)=4x-ex.又g′(0)<0,g′(2)>0,∴g(x)在(0,2)内至少存在一个极值点,∴f(x)=2x2-e|x|在(0,2)内至少存在一个极值点,排除C.故选D.]
2.已知函数f(x)=ax4-4ax3+b(a>0),x∈[1,4],f(x)的最大值为3,最小值为-6,则a+b=( )
A. B. C. D.
C [f′(x)=4ax3-12ax2.令f′(x)=0,得x=3或x=0(舍去).当1≤x<3时,f′(x)<0,当3
3.函数y=xex在其极值点处的切线方程为__________.
y=- [由题知y′=ex+xex,令y′=0,解得x=-1,代入函数解析式可得极值点的坐标为,又极值点处的切线为平行于x轴的直线,故方程为y=-.]
4.若函数f(x)=2x2-ln x在定义域内的一个子区间(k-1,k+1)上不是单调函数,则实数k的取值范围是__________.
[由题意可知函数f(x)的定义域为(0,+∞),f′(x)=4x-=.由f′(x)>0,得函数f(x)的单调增区间为;由f′(x)<0,得函数f(x)的单调减区间为.由于函数f(x)在区间(k-1,k+1)上不是单调函数,所以k-1<
(1)若曲线y=f(x)在点A(2,f(2))处的切线斜率为2,求实数a的值;
(2)当x>0时,求证:f(x)≥a;
(3)若在区间(1,e)上,>1恒成立,求实数a的取值范围.
[解] (1)∵f′(x)=,∴f′(2)==2,∴a=4.
(2)证明:令g(x)=f(x)-a,则g(x)=aln x-1+,
g′(x)=a.
令g′(x)>0,即a>0,解得x>1,
令g′(x)<0,即a<0,解得x<1,又x>0,∴0
∴g(x)的最小值为g(1)=0,∴f(x)≥a.
(3)令h(x)=aln x+1-x,则h′(x)=-1,
令h′(x)>0,解得x
当a≥e时,h(x)在(1,e)上是增函数,∴h(x)>h(1)=0;
当1
当a≤1时,h(x)在(1,e)上单调递减,则只需h(e)≥0,
又h(e)=a+1-e<0,∴此时a不存在.
综上,实数a的取值范围为[e-1,+∞).
