2.1空间点,线,面的位置关系
图片预览






文档简介
课件76张PPT。2.1.1 平面YOUR SITE HERE生活中有哪些给事物给我们以平面的形象?YOUR SITE HERE平面的形象YOUR SITE HERE平面的概念及其表示平静的海面平面的形象平整的纸张桌面、黑板面1.无限延展2.不计大小3.不计厚薄 (没有边界) (无所谓面积) (没有质量)概念 几何里所说的“平面”(plane)就是从这样的一些物体中抽象出来的.但是,几何里的平面是无限延展的.YOUR SITE HERE一、判断下列各题的说法正确与否:
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是 4 cm 2; ( )
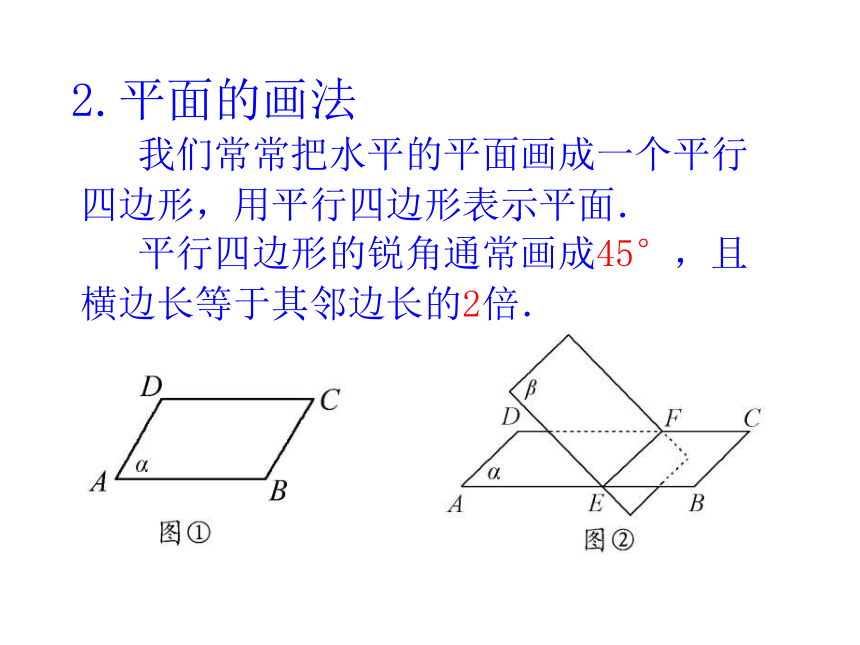
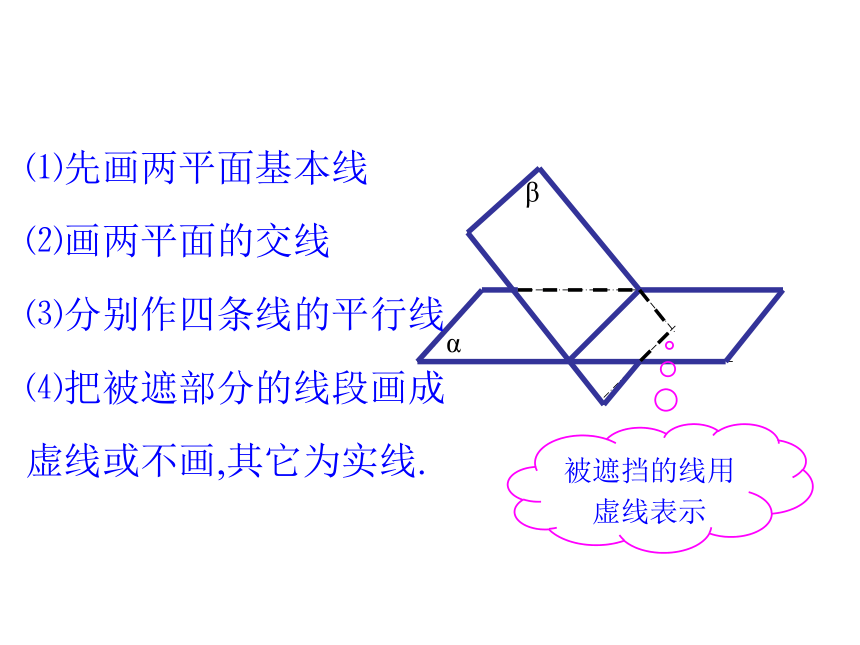
5、一个平面可以把空间分成两部分. ( ) 我们常常把水平的平面画成一个平行四边形,用平行四边形表示平面. 平行四边形的锐角通常画成45°,且横边长等于其邻边长的2倍.2.平面的画法⑴先画两平面基本线
⑵画两平面的交线
⑶分别作四条线的平行线
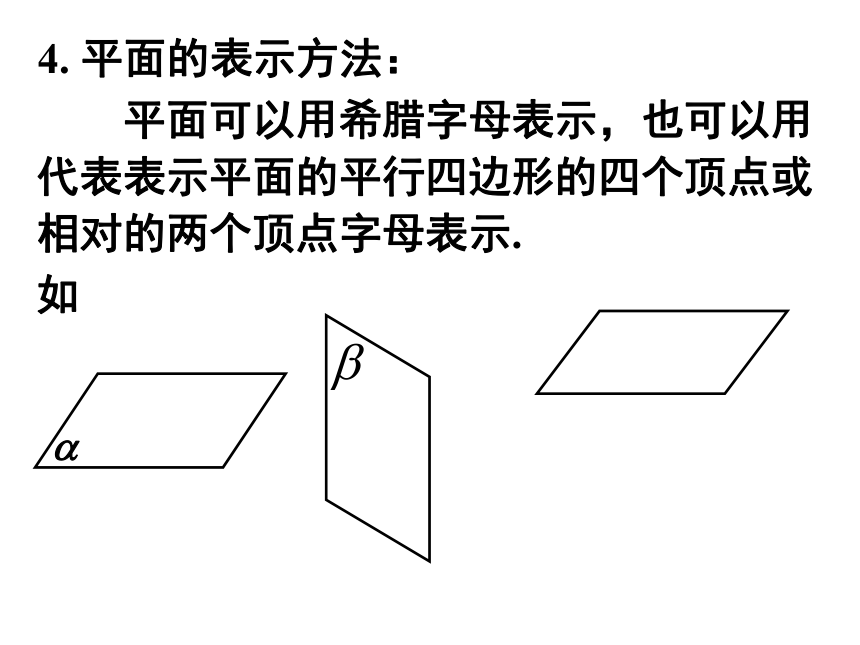
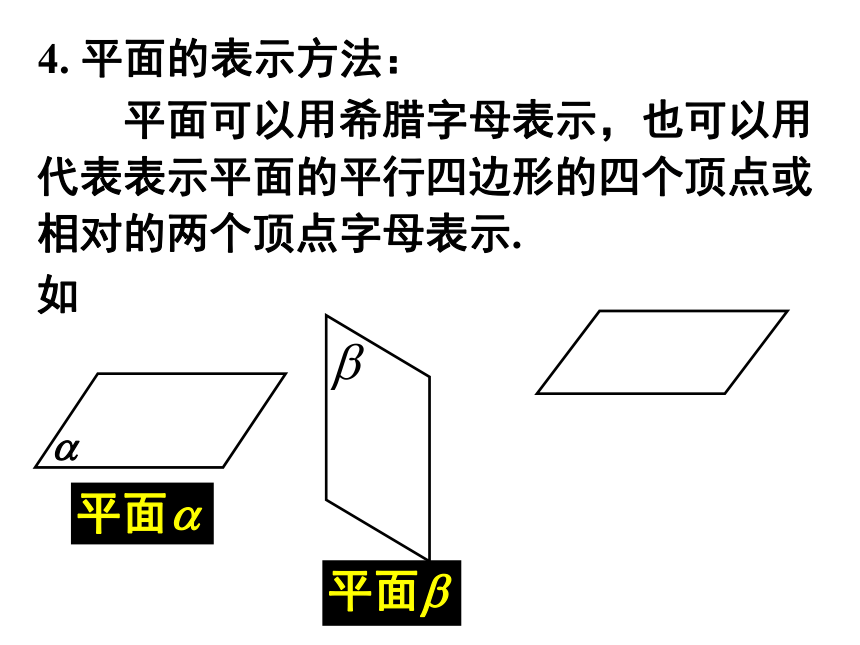
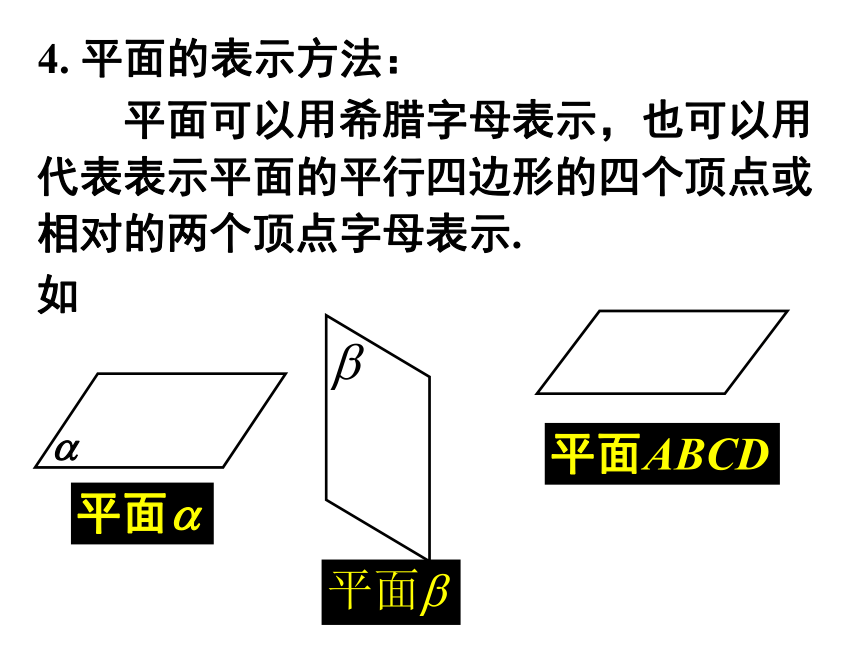
⑷把被遮部分的线段画成虚线或不画,其它为实线.αβ被遮挡的线用虚线表示 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法: 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法:如 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法:如 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法:如 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法:如 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法:如YOUR SITE HERE点A,线l,面α的基本关系1.点和直线的关系?2.点和平面的关系?3.直线和平面的关系?(1)点在直线上(2)点在直线外lAA(1)点在平面内(2)点在平面外AAlAl(1)直线在平面内l(2)直线在平面外l例2. 把下列语句用集合符号表示,并画
出直观图.
(1) 点A在平面?内,点B不在平面?内,
点A,B都在直线a上;
(2) 平面?与平面?相交于直线m,直线a
在平面?内且平行于直线m.例2. 把下列语句用集合符号表示,并画
出直观图.
(1) 点A在平面?内,点B不在平面?内,
点A,B都在直线a上;
(2) 平面?与平面?相交于直线m,直线a
在平面?内且平行于直线m.ABa? 把下列语句用集合符号表示,并画
出直观图.
(1) 点A在平面?内,点B不在平面?内,
点A,B都在直线a上;
(2) 平面?与平面?相交于直线m,直线a
在平面?内且平行于直线m.??maABa?YOUR SITE HERE 如果直线 l 与平面α有一个公点, 直线 l 是否在平面α内?有两个公共点呢?探究1:YOUR SITE HERE 公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.作用:判断直线是否在平面
内的依据.符
号
语
言:图形语言: 生活中经常看到用三角架支撑照相机.测量员用三角架支撑测量用的平板仪.YOUR SITE HERE过一点可以做几条直线?两点呢?过空间中一点可以做几个平面?两点呢?不共线的三点呢?探究2:YOUR SITE HERE作用:确定一个平面的主要依据. 公理2 过不在一条直线上的三点,有且只有一个平面.图形语言:存在性唯一性符号语言:公理2 过不在同一直线上的三点,有且只
有一个平面.推论1 一条直线和直线外一点唯一确定一
个平面.推论2 两条相交直线唯一确定一个平面.AClB公理2 过不在同一直线上的三点,有且只
有一个平面.推论1 一条直线和直线外一点唯一确定一
个平面.推论2 两条相交直线唯一确定一个平面.推论3 两条平行直线唯一确定一个平面.ACBlYOUR SITE HERE 把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?探究3:YOUR SITE HERE 公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.②判断点在直线上平面公理符号语言:图形语言:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.过不在一条直线上的三点,有且只有一个平面.文字语言图形语言符号语言探
究
1探
究
3探
究
2如果一条直线上的两点在一个平面内,那么这条直线在此平面内.(2) 经过同一点的三条直线确定一个平面.
(3) 若点A∈直线a,点A∈平面?,则a??.
(4) 平面?与平面?相交,它们只有有限个例4. 判断下列命题是否正确:( )(1) 经过三点确定一个平面. ( )( )( )公共点.例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.(1)(2)YOUR SITE HERE(1)两个平面的公共点的个数可能有 ( )(2)三个平面两两相交,则它们交线的条数 ( )A.0 B.1 C.2 D.0或无数A.最多4条最少3条 B.最多3条最少1条
C.最多3条最少2条 D.最多2条最少1条 (3)已知空间四点中,无三点共线,则可确定( )A.一个平面 B.四个平面
C.一个或四个平面 D.无法确定平面的个数DBC选择题YOUR SITE HERE错误小竞赛YOUR SITE HERE正确YOUR SITE HERE③由点A,O,C可以确定一个平面;错误YOUR SITE HERE正确正确探究1:
一个平面把空间分成几部分?
两个平面把空间分成几部分?
三个互不重合的平面把空间分成几部分?图(1) 图(2)典例赏析实例引入平面平面的画法和表示点和平面的位置关系平面的三个公理YOUR SITE HERE三条平面公理 公理3 公理2 公理1 Thank You!LOGO立体几何2.1.2空间中直线与直线
之间的位置关系判断下列命题对错:
1.如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。( )
2.将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。 ( )
3.四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。 ( )
4.一条直线和一个点可以确定一个平面。( )
5.如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。 ( )?????温故知新平面内两条直线的位置关系复习引入螺 母新课探究观察下列图形,说说空间中两条直线的位置关系探究一立交桥 不同在任何一个平面内的两条直线叫做异面直线。没有只有一个没有共面不共面共面1.异面直线的定义2.异面直线的画法说明: 画异面直线时 , 为了体现
它们不共面的特点。常借
助一个或两个平面来衬托.如图:(1)(3)(2)a与b是相交直线a与b是平行直线a与b是异面直线答:不一定:它们可能异面,可能相交,也可能平行。 分别在两个平面内的两条直线是否一定异面?思考3.异面直线的判定方法:①不同在任何一个平面内。②既不相交也不平行的直线。③连结平面内一点与平面外一点的直线和这个平面内不经过此点的直线是异面直线。 按平面基本性质分同在一个平面内相交直线平行直线 不同在任何一个平面内:异面直线 有一个公共点: 按公共点个数分相交直线无 公 共 点平行直线异面直线 空间中直线与直线之间的位置关系 下图长方体中平行相交异面② BD 和FH是 直线① EC 和BH是 直线③BH 和DC是 直线(2).与棱 A B 所在直线异面的棱共有 条?4分别是 :CG、HD、GF、HE(1)说出以下各对线段的位置关系?练习 在如图所示的正方体中,指出哪些棱
所在的直线与直线BA1是异面直线?ABCDA1B1D1C1 已知M、N分别是长方体的棱C1D1与CC1
上的点,那么MN与AB所在的直线相交吗?ABCDA1B1D1C1MN填空:
1、空间两条不重合的直线的位置关系有________、 ________、 ________三种。
2、没有公共点的两条直线可能是________直线,也有可能是
________直线。
3、和两条异面直线中的一条平行的直线与另一条的位置关系
有______________。
平行相交异面平行异面相交、异面我们知道,在同一平面内, 如果两条直线都和第三条直线平行,
那么这两条直线互相平行.在空间这一规律是否还成立呢?观察 : 将一张纸如图进行折叠 , 则各折痕及边 a, b, c, d, e, …
之间有何关系?a∥b ∥c ∥d ∥e ∥ …公理4:在空间平行于同一条直线的两条直线互相平行.———平行线的传递性公理4 平行于同一条直线的两条直线互相平行.注:
1.直线a,b,c 两两平行,可记为a // b // c .2.公理4所表述的性质,叫做空间平行线的传递性.3.证明空间两直线平行 的方法:
(1) 定义法:一要证两直线在同一平面内;二要证两直线没有公共点(反证法)
(2) 公理法平行公理 空间直线的平行关系:例2.已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC, CD,DA的中点,连结EF,FG,GH,HE,求证:EFGH是一个平行四边形。
?证明:连结BD
∵ EH是△ABD的中位线
∴EH ∥BD且EH =1/2 BD
同理,FG ∥BD且FG =1/2 BD
∴EH ∥FG且EH =FG
∴EFGH是一个平行四边形
如果再加上条件AC = BD,那么四边形EFGH是什么图形? 在平面内, 我们可以证明 “ 如果一个角的两边与另一个角的
两边分别平行,那么这两个角相等或互补 ”.空间中这一结
论是否仍然成立呢?定理(等角定理):空间中,如果两个角的两边分别对应平行,
那么这两个角相等或互补.观察 :如图所示,长方体ABCD-A1B1C1D1中, ∠ADC与∠A1D1C1 ,
∠ADC与∠A1B1C1两边分别对应平行,这两组角的大小
关系如何?异面直线所成的角 在平面内,两条直线相交成四
个角, 其中不大于90度的角称为它
们的夹角, 用以刻画两直线的错开
程度, 如图. 在空间,如图所示, 正方体ABCD-EFGH中, 异面直线AB与HF的错开程度可以怎样来刻画呢?问题提出复习回顾如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作 a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角.?任选若两条异面直线所成角为90°,则称它们互相垂直.异面直线a与b垂直也记作a⊥b.平移 两条异面直线所成的角注1:异面直线a、b所成角,只与a、b的相互位置有关, 而与点O位置无关.一般常把点O取在直线a或b上.注2:异面直线所成角的取值范围:如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直。因此,异面直线所成角的范围是(0, ]注3:特例:填空:
1、空间两条不重合的直线的位置关系有________、 ________、 ________三种。
2、没有公共点的两条直线可能是________直线,也有可能是
________直线。
3、和两条异面直线中的一条平行的直线与另一条的位置关系
有______________。
4 、过已知直线上一点可以作______条直线与已知直线垂直。
5 、过已知直线外一点可以作______条直线与已知直线垂直。平行相交异面平行异面无数无数相交、异面
1、分别在两个平面内的两条直线一定是异面直线。( )
2、空间两条不相交的直线一定是异面直线。 ( )
3、垂直于同一条直线的两条直线必平行。 ( )
4、若一条直线垂直于两条平行直线中的一条,则它一定与另一条直线垂直。 ( ) ????判断对错:例:ABCDB1A1C1D1所以B A1和 CC1所成的角为450例:在正方体AC1中,求异面直线A1B和B1C所成的角A1B和B1C所成的角为60°例:在正方体AC1中,求异面直线AC和BD1所成的角ABCDB1A1C1D1OM在空间四边形S-ABC中,SA⊥BC且 SA=BC, E, F分别为SC、AB 的中点,那么异面直线EF 与SA 所成的角等于( )CD(A)300 (B)450 (C)600 (D)900练习BCABDFEG 如图,在长方体中,已知AA1=AD=a,
AB= a,求AB1与BC1所成的角的余弦值.CBADA1B1C1D1aa探究:HGCADBEF如图是一个正方体的展开图,如果将它还原为正方体, 那么 AB,
CD , EE , GH这四条线段所在直线是异面直线的有 对?答:共有三对小结:
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是 4 cm 2; ( )
5、一个平面可以把空间分成两部分. ( ) 我们常常把水平的平面画成一个平行四边形,用平行四边形表示平面. 平行四边形的锐角通常画成45°,且横边长等于其邻边长的2倍.2.平面的画法⑴先画两平面基本线
⑵画两平面的交线
⑶分别作四条线的平行线
⑷把被遮部分的线段画成虚线或不画,其它为实线.αβ被遮挡的线用虚线表示 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法: 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法:如 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法:如 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法:如 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法:如 平面可以用希腊字母表示,也可以用
代表表示平面的平行四边形的四个顶点或
相对的两个顶点字母表示.4. 平面的表示方法:如YOUR SITE HERE点A,线l,面α的基本关系1.点和直线的关系?2.点和平面的关系?3.直线和平面的关系?(1)点在直线上(2)点在直线外lAA(1)点在平面内(2)点在平面外AAlAl(1)直线在平面内l(2)直线在平面外l例2. 把下列语句用集合符号表示,并画
出直观图.
(1) 点A在平面?内,点B不在平面?内,
点A,B都在直线a上;
(2) 平面?与平面?相交于直线m,直线a
在平面?内且平行于直线m.例2. 把下列语句用集合符号表示,并画
出直观图.
(1) 点A在平面?内,点B不在平面?内,
点A,B都在直线a上;
(2) 平面?与平面?相交于直线m,直线a
在平面?内且平行于直线m.ABa? 把下列语句用集合符号表示,并画
出直观图.
(1) 点A在平面?内,点B不在平面?内,
点A,B都在直线a上;
(2) 平面?与平面?相交于直线m,直线a
在平面?内且平行于直线m.??maABa?YOUR SITE HERE 如果直线 l 与平面α有一个公点, 直线 l 是否在平面α内?有两个公共点呢?探究1:YOUR SITE HERE 公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.作用:判断直线是否在平面
内的依据.符
号
语
言:图形语言: 生活中经常看到用三角架支撑照相机.测量员用三角架支撑测量用的平板仪.YOUR SITE HERE过一点可以做几条直线?两点呢?过空间中一点可以做几个平面?两点呢?不共线的三点呢?探究2:YOUR SITE HERE作用:确定一个平面的主要依据. 公理2 过不在一条直线上的三点,有且只有一个平面.图形语言:存在性唯一性符号语言:公理2 过不在同一直线上的三点,有且只
有一个平面.推论1 一条直线和直线外一点唯一确定一
个平面.推论2 两条相交直线唯一确定一个平面.AClB公理2 过不在同一直线上的三点,有且只
有一个平面.推论1 一条直线和直线外一点唯一确定一
个平面.推论2 两条相交直线唯一确定一个平面.推论3 两条平行直线唯一确定一个平面.ACBlYOUR SITE HERE 把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?探究3:YOUR SITE HERE 公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.②判断点在直线上平面公理符号语言:图形语言:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.过不在一条直线上的三点,有且只有一个平面.文字语言图形语言符号语言探
究
1探
究
3探
究
2如果一条直线上的两点在一个平面内,那么这条直线在此平面内.(2) 经过同一点的三条直线确定一个平面.
(3) 若点A∈直线a,点A∈平面?,则a??.
(4) 平面?与平面?相交,它们只有有限个例4. 判断下列命题是否正确:( )(1) 经过三点确定一个平面. ( )( )( )公共点.例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.(1)(2)YOUR SITE HERE(1)两个平面的公共点的个数可能有 ( )(2)三个平面两两相交,则它们交线的条数 ( )A.0 B.1 C.2 D.0或无数A.最多4条最少3条 B.最多3条最少1条
C.最多3条最少2条 D.最多2条最少1条 (3)已知空间四点中,无三点共线,则可确定( )A.一个平面 B.四个平面
C.一个或四个平面 D.无法确定平面的个数DBC选择题YOUR SITE HERE错误小竞赛YOUR SITE HERE正确YOUR SITE HERE③由点A,O,C可以确定一个平面;错误YOUR SITE HERE正确正确探究1:
一个平面把空间分成几部分?
两个平面把空间分成几部分?
三个互不重合的平面把空间分成几部分?图(1) 图(2)典例赏析实例引入平面平面的画法和表示点和平面的位置关系平面的三个公理YOUR SITE HERE三条平面公理 公理3 公理2 公理1 Thank You!LOGO立体几何2.1.2空间中直线与直线
之间的位置关系判断下列命题对错:
1.如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。( )
2.将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。 ( )
3.四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。 ( )
4.一条直线和一个点可以确定一个平面。( )
5.如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。 ( )?????温故知新平面内两条直线的位置关系复习引入螺 母新课探究观察下列图形,说说空间中两条直线的位置关系探究一立交桥 不同在任何一个平面内的两条直线叫做异面直线。没有只有一个没有共面不共面共面1.异面直线的定义2.异面直线的画法说明: 画异面直线时 , 为了体现
它们不共面的特点。常借
助一个或两个平面来衬托.如图:(1)(3)(2)a与b是相交直线a与b是平行直线a与b是异面直线答:不一定:它们可能异面,可能相交,也可能平行。 分别在两个平面内的两条直线是否一定异面?思考3.异面直线的判定方法:①不同在任何一个平面内。②既不相交也不平行的直线。③连结平面内一点与平面外一点的直线和这个平面内不经过此点的直线是异面直线。 按平面基本性质分同在一个平面内相交直线平行直线 不同在任何一个平面内:异面直线 有一个公共点: 按公共点个数分相交直线无 公 共 点平行直线异面直线 空间中直线与直线之间的位置关系 下图长方体中平行相交异面② BD 和FH是 直线① EC 和BH是 直线③BH 和DC是 直线(2).与棱 A B 所在直线异面的棱共有 条?4分别是 :CG、HD、GF、HE(1)说出以下各对线段的位置关系?练习 在如图所示的正方体中,指出哪些棱
所在的直线与直线BA1是异面直线?ABCDA1B1D1C1 已知M、N分别是长方体的棱C1D1与CC1
上的点,那么MN与AB所在的直线相交吗?ABCDA1B1D1C1MN填空:
1、空间两条不重合的直线的位置关系有________、 ________、 ________三种。
2、没有公共点的两条直线可能是________直线,也有可能是
________直线。
3、和两条异面直线中的一条平行的直线与另一条的位置关系
有______________。
平行相交异面平行异面相交、异面我们知道,在同一平面内, 如果两条直线都和第三条直线平行,
那么这两条直线互相平行.在空间这一规律是否还成立呢?观察 : 将一张纸如图进行折叠 , 则各折痕及边 a, b, c, d, e, …
之间有何关系?a∥b ∥c ∥d ∥e ∥ …公理4:在空间平行于同一条直线的两条直线互相平行.———平行线的传递性公理4 平行于同一条直线的两条直线互相平行.注:
1.直线a,b,c 两两平行,可记为a // b // c .2.公理4所表述的性质,叫做空间平行线的传递性.3.证明空间两直线平行 的方法:
(1) 定义法:一要证两直线在同一平面内;二要证两直线没有公共点(反证法)
(2) 公理法平行公理 空间直线的平行关系:例2.已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC, CD,DA的中点,连结EF,FG,GH,HE,求证:EFGH是一个平行四边形。
?证明:连结BD
∵ EH是△ABD的中位线
∴EH ∥BD且EH =1/2 BD
同理,FG ∥BD且FG =1/2 BD
∴EH ∥FG且EH =FG
∴EFGH是一个平行四边形
如果再加上条件AC = BD,那么四边形EFGH是什么图形? 在平面内, 我们可以证明 “ 如果一个角的两边与另一个角的
两边分别平行,那么这两个角相等或互补 ”.空间中这一结
论是否仍然成立呢?定理(等角定理):空间中,如果两个角的两边分别对应平行,
那么这两个角相等或互补.观察 :如图所示,长方体ABCD-A1B1C1D1中, ∠ADC与∠A1D1C1 ,
∠ADC与∠A1B1C1两边分别对应平行,这两组角的大小
关系如何?异面直线所成的角 在平面内,两条直线相交成四
个角, 其中不大于90度的角称为它
们的夹角, 用以刻画两直线的错开
程度, 如图. 在空间,如图所示, 正方体ABCD-EFGH中, 异面直线AB与HF的错开程度可以怎样来刻画呢?问题提出复习回顾如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作 a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角.?任选若两条异面直线所成角为90°,则称它们互相垂直.异面直线a与b垂直也记作a⊥b.平移 两条异面直线所成的角注1:异面直线a、b所成角,只与a、b的相互位置有关, 而与点O位置无关.一般常把点O取在直线a或b上.注2:异面直线所成角的取值范围:如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直。因此,异面直线所成角的范围是(0, ]注3:特例:填空:
1、空间两条不重合的直线的位置关系有________、 ________、 ________三种。
2、没有公共点的两条直线可能是________直线,也有可能是
________直线。
3、和两条异面直线中的一条平行的直线与另一条的位置关系
有______________。
4 、过已知直线上一点可以作______条直线与已知直线垂直。
5 、过已知直线外一点可以作______条直线与已知直线垂直。平行相交异面平行异面无数无数相交、异面
1、分别在两个平面内的两条直线一定是异面直线。( )
2、空间两条不相交的直线一定是异面直线。 ( )
3、垂直于同一条直线的两条直线必平行。 ( )
4、若一条直线垂直于两条平行直线中的一条,则它一定与另一条直线垂直。 ( ) ????判断对错:例:ABCDB1A1C1D1所以B A1和 CC1所成的角为450例:在正方体AC1中,求异面直线A1B和B1C所成的角A1B和B1C所成的角为60°例:在正方体AC1中,求异面直线AC和BD1所成的角ABCDB1A1C1D1OM在空间四边形S-ABC中,SA⊥BC且 SA=BC, E, F分别为SC、AB 的中点,那么异面直线EF 与SA 所成的角等于( )CD(A)300 (B)450 (C)600 (D)900练习BCABDFEG 如图,在长方体中,已知AA1=AD=a,
AB= a,求AB1与BC1所成的角的余弦值.CBADA1B1C1D1aa探究:HGCADBEF如图是一个正方体的展开图,如果将它还原为正方体, 那么 AB,
CD , EE , GH这四条线段所在直线是异面直线的有 对?答:共有三对小结:
