冀教版数学九年级上25.4《相似三角形的判定》试卷(含答案解析)
文档属性
| 名称 | 冀教版数学九年级上25.4《相似三角形的判定》试卷(含答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-13 00:00:00 | ||
图片预览


文档简介
相似三角形的判定
时间:100分钟 总分:100
题号 一 二 三 四 总分
得分
一、选择题(本大题共7小题,共28.0分)
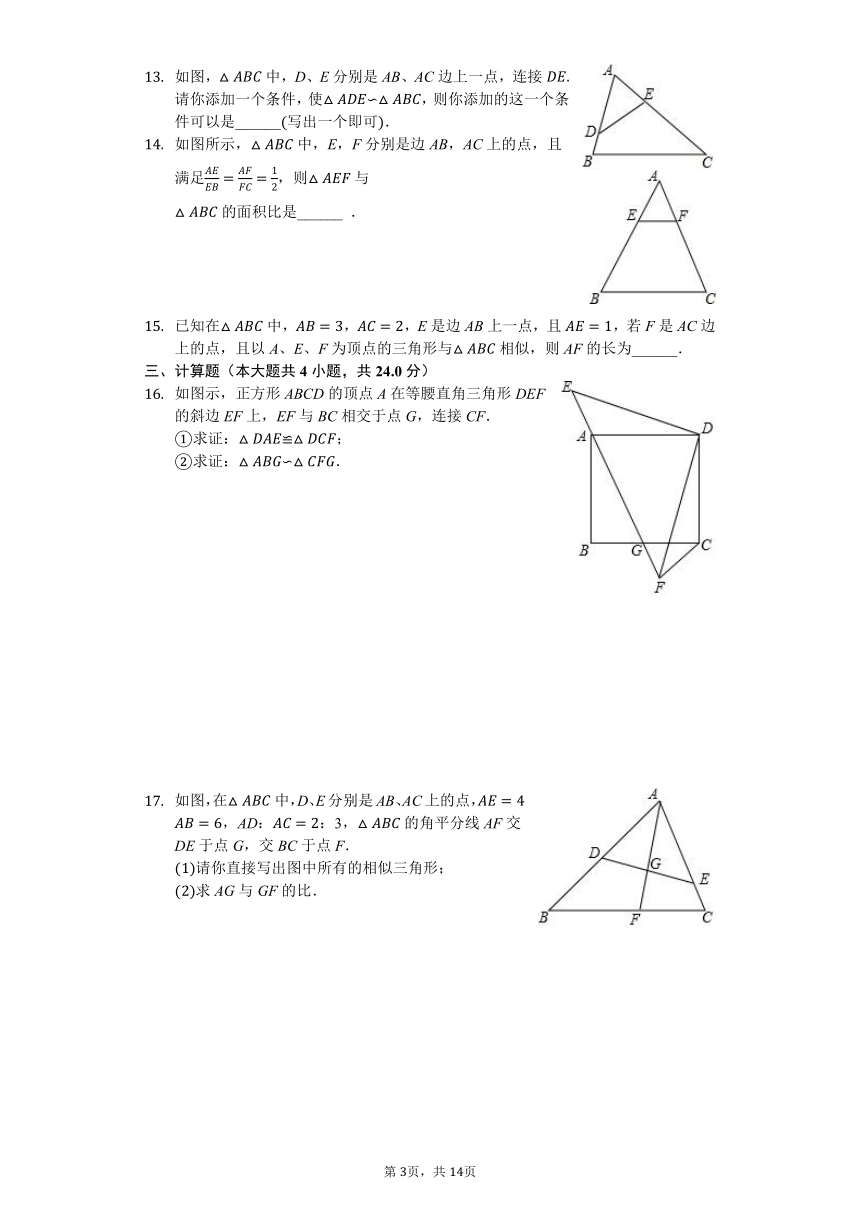
如图,在中,点P在边AB上,则在下列四个条件中::;;;,能满足与相似的条件是
A. B. C. D.
下列的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与相似的是
?
A. B. C. D.
如图所示,每个小正方形的边长均为1,则下列A、B、C、D四个图中的三角形阴影部分与相似的是
?
A. B. C. D.
如图,在中,点D,E分别在边AB,AC上,下列条件中不能判断∽的是
A.
B.
C.
D.
如图,在正方形ABCD中,点E,F分别在BC,CD上,且,将绕点A顺时针旋转,使点E落在点处,则下列判断不正确的是
A. 是等腰直角三角形 B. AF垂直平分
C. ∽ D. 是等腰三角形
如图,在中,,,点D在AC上,且,如果要在AB上找一点E,使与相似,则AE的长为
A. B. C. 3 D. 或
如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:,,,,,使与一定相似的有
A. B. C. D.
二、填空题(本大题共8小题,共32.0分)
如图,已知中,D为边AC上一点,P为边AB上一点,,,,当AP的长度为______ 时,和相似.
如图,在中,、E分别为边AB、AC上的点,,点F为BC边上一点,添加一个条件:______,可以使得与相似只需写出一个
在中,,,点D在边AB上,且,点E在边AC上,当______时,以A、D、E为顶点的三角形与相似.
如图,,,,,,点p在BD上移动,当 ______ 时,和相似.
如图,在中,点E,F分别在AB,AC上,若∽,则需要增加的一个条件是______写出一个即可
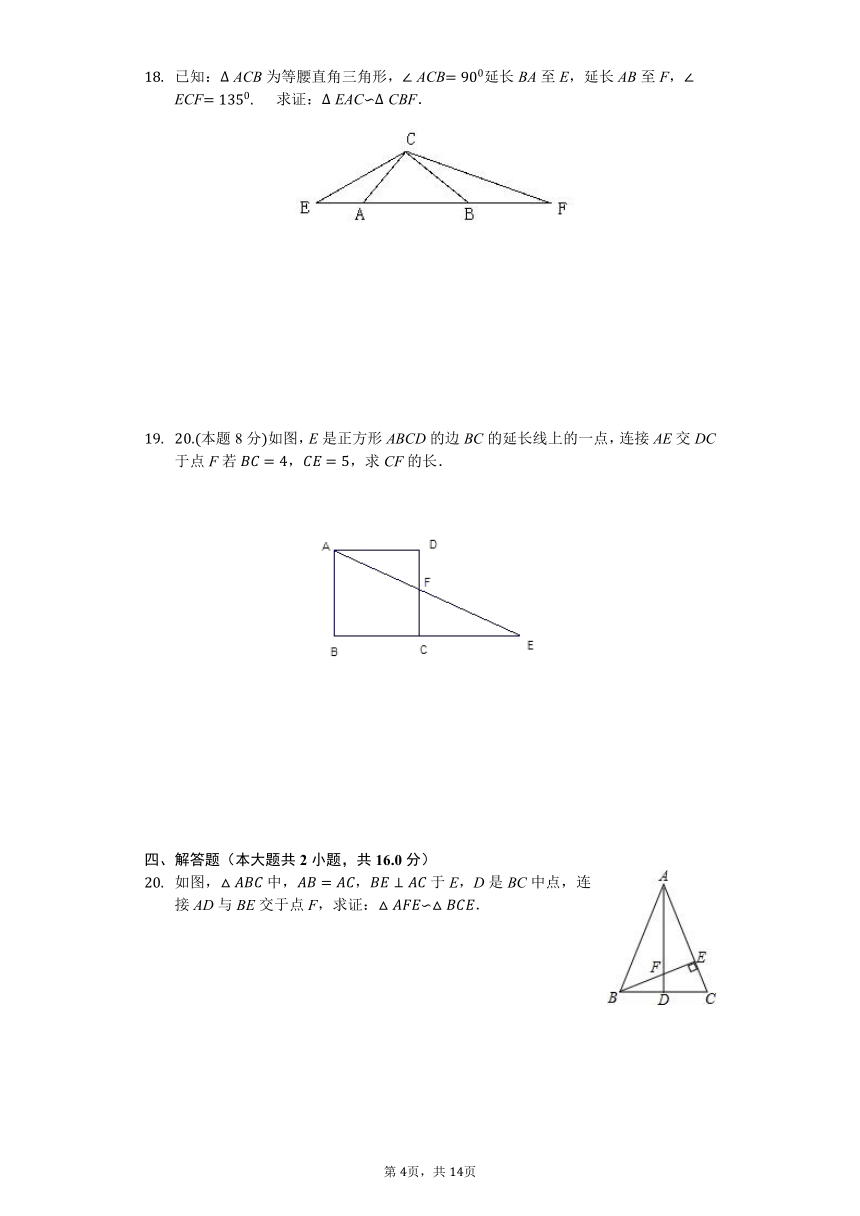
如图,中,D、E分别是AB、AC边上一点,连接请你添加一个条件,使∽,则你添加的这一个条件可以是______写出一个即可.
如图所示,中,E,F分别是边AB,AC上的点,且满足,则与
的面积比是______ .
已知在中,,,E是边AB上一点,且,若F是AC边上的点,且以A、E、F为顶点的三角形与相似,则AF的长为______.
三、计算题(本大题共4小题,共24.0分)
如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
求证:≌;??????
求证:∽.
如图,在中,D、E分别是AB、AC上的点,,,AD::3,的角平分线AF交DE于点G,交BC于点F.
请你直接写出图中所有的相似三角形;
求AG与GF的比.
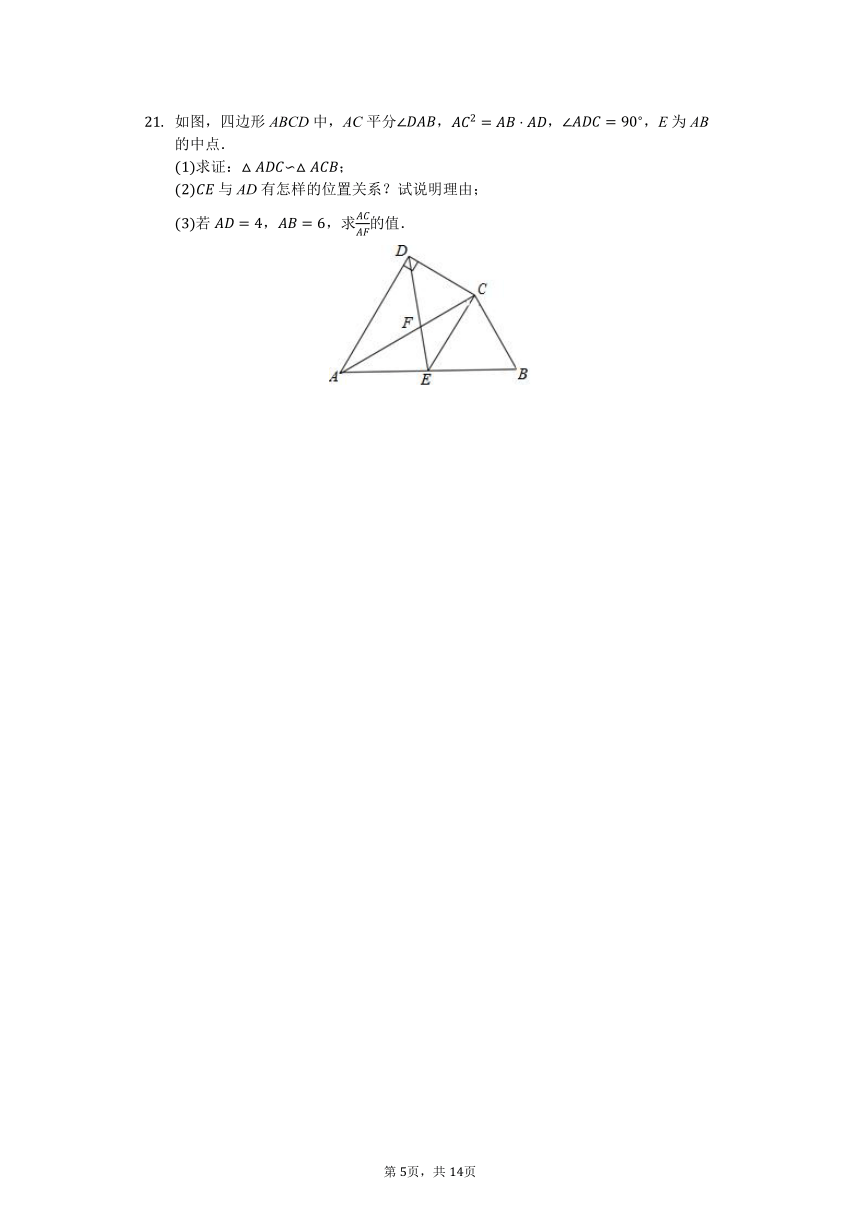
已知: ACB为等腰直角三角形, ACB延长BA至E,延长AB至F, ECF???? 求证: EAC∽ CBF.
本题8分如图,E是正方形ABCD的边BC的延长线上的一点,连接AE交DC于点F若,,求CF的长.
?
四、解答题(本大题共2小题,共16.0分)
如图,中,,于E,D是BC中点,连接AD与BE交于点F,求证:∽.
如图,四边形ABCD中,AC平分,,,E为AB的中点.
求证:∽;
与AD有怎样的位置关系?试说明理由;
若,,求的值.
答案和解析
【答案】
1. D 2. B 3. B 4. A 5. D 6. D 7. A
8. 4或9??
9. ,或??
10. 或??
11. 或12cm或2cm??
12. ??
13. ??
14. 1:9??
15. 或??
16. 证明:正方形ABCD,等腰直角三角形EDF,
,,,
,
,
在和中,
,
≌;
延长BA到M,交ED于点M,
≌,
,即,
,
,
,
,
,
∽.??
17. 解:∽,∽,∽;
,,
,
又,
∽,
,
为角平分线,
∽,
,
.??
18. 为等腰直角三角形,,
?,
,
,
,
,
又,
,
在和中,
,,
∽
??
19. 解:四边形ABCD是正方形,
,,
,
又,,
∽,
::CE,
,,
::5,
? ? ?
??
20. 证明:,D是BC中点,
,
,
,
,
,
,
,
,
∽.??
21. 解:平分,
,
又,
::AB,
∽;
,
理由:∽,
,
又为AB的中点,
,
,
,
,
;
,,,
,
,,
∽,
,
.??
【解析】
1. 解:当,,
所以∽;
当,,
所以∽;
当,
即AC::AC,
所以∽;
当,即PC::AB,
而,
所以不能判断和相似.
故选D.
根据有两组角对应相等的两个三角形相似可对进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对进行判断.
本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.
2. 解:根据勾股定理,,,
所以,夹直角的两边的比为,
观各选项,只有B选项三角形符合,与所给图形的三角形相似.
故选:B.
可利用正方形的边把对应的线段表示出来,利用三边对应成比例两个三角形相似,分别计算各边的长度即可解题.
此题考查了勾股定理在直角三角形中的运用,三角形对应边比值相等判定三角形相似的方法,本题中根据勾股定理计算三角形的三边长是解题的关键.
3. 解:小正方形的边长为1,
在中,,,,
A中,一边,一边,一边,三边与中的三边不能对应成比例,故两三角形不相似故A错误;
B中,一边,一边,一边,
有,即三边与中的三边对应成比例,故两三角形相似故B正确;
C中,一边,一边,一边,三边与中的三边不能对应成比例,故两三角形不相似故C错误;
D中,一边,一边,一边,三边与中的三边不能对应成比例,故两三角形不相似故D错误.
故选:B.
根据相似三角形的判定,易得出的三边的边长,故只需分别求出各选项中三角形的边长,分析两三角形对应边是否成比例即可.
本题考查了相似三角形的判定识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法.
4. 解:,
当或时,∽;
当即时,∽.
故选:A.
根据相似三角形的判定定理进行判定即可.
本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.
5. 解:将绕点A顺时针旋转,使点E落在点处,
,,
是等腰直角三角形,故A正确;
将绕点A顺时针旋转,使点E落在点处,
,
四边形ABCD是正方形,
,
,
,
,
,
,
垂直平分,故B正确;
,,
,
,
∽,故C正确;
,但不一定等于,
不一定是等腰三角形,故D错误;
故选D.
由旋转的性质得到,,于是得到是等腰直角三角形,故A正确;由旋转的性质得到,由正方形的性质得到,推出,于是得到AF垂直平分,故B正确;根据余角的性质得到,于是得到∽,故C正确;由于,但不一定等于,于是得到不一定是等腰三角形,故D错误.
本题考查了旋转的性质,正方形的性质,相似三角形的判定,等腰直角三角形的判定,线段垂直平分线的判定,正确的识别图形是解题的关键.
6. 解:是公共角,
当,即时,∽,
解得:;
当,即时,∽,
解得:,
的长为:或.
故选D.
由是公共角,分别从当,即时,∽与当,即时,∽,去分析求解即可求得答案.
此题考查了相似三角形的判定注意分类讨论思想的应用.
7. 解:,,
∽,正确;
,,
∽,正确;
,,
∽,正确;
由,或不能证明与相似.
故选:A.
由两角相等的两个三角形相似得出正确,由两边成比例且夹角相等的两个三角形相似得出正确;即可得出结果.
本题考查了相似三角形的判定定理:
两角对应相等的两个三角形相似;
两边对应成比例且夹角相等的两个三角形相似;
三边对应成比例的两个三角形相似;
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
8. 解:当∽时,
,
,
解得:,
当∽时,
,
,
解得:,
当AP的长度为4或9时,和相似.
故答案为:4或9.
分别根据当∽时,当∽时,求出AP的长即可.
此题主要考查了相似三角形的判定与性质,利用倒推法以及分类讨论得出是解题关键.
9. 解:,或.
理由:,,
∽,
当时,∽,
∽.
当时,,
∽.
故答案为,或.
结论:,或根据相似三角形的判定方法一一证明即可.
本题考查相似三角形的判定和性质平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
10. 解:当时,
,
∽,
此时;
当时,
,
∽,
此时;
故答案为:或.
若A,D,E为顶点的三角形与相似时,则或,分情况进行讨论后即可求出AE的长度.
本题考查了相似三角形的判定,熟练掌握相似三角形的判定方法,解题的关键是分两种情况进行讨论.
11. 解:由,,,
设,则,
若∽,
则,
即,
变形得:,即,
因式分解得:,
解得:,,
所以或12cm时,∽;
若∽,
则,
即,解得:,
,
综上,或12cm或时,∽.
故答案为:或12cm或2cm.
设出,由表示出PD的长,若∽,根据相似三角形的对银边成比例可得比例式,把各边的长代入即可列出关于x的方程,求出方程的解即可得到x的值,即为PB的长.
此题考查了相似三角形的判定与性质,相似三角形的性质有相似三角形的对应边成比例,对应角相等;相似三角形的判定方法有:1、两对对应角相等的两三角形相似;2、两对对应边成比例且夹角相等的两三角形相似;3、三边对应成比例的两三角形相似,本题属于条件开放型探究题,其解法:类似于分析法,假设结论成立,逐步探索其成立的条件.
12. 解:当时,∽.
故答案为.
利用平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似进行添加条件.
本题考查了相似三角形的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似.
13. 解:,
当时,∽.
故答案为.
利用有两组角对应相等的两个三角形相似添加条件.
本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.
14. 解:
,
,
又,
∽,
与的面积比:9,
故答案为:1:9.
由已知条件易证∽,根据相似三角形的性质即可求出与的面积比.
本题考查了相似三角形的判定和性质,熟悉相似三角形的性质:相似三角形的面积比是相似比的平方是解题关键.
15. 解:,
以A、E、F为顶点的三角形与相似,有∽和∽两种情况:
如图1:
当时,∽时,即,解得:;
如图2:
当时,∽时,即,解得:.
所以或.
故答案为或.
根据相似三角形的相似比求AF,注意分情况考虑.
本题考查了相似三角形的判定,熟练掌握相似三角形的判定定理,分情况讨论是解决本题的关键.
16. 由正方形ABCD与等腰直角三角形DEF,得到两对边相等,一对直角相等,利用SAS即可得证;
由第一问的全等三角形的对应角相等,根据等量代换得到,再由对顶角相等,利用两对角相等的三角形相似即可得证.
此题考查了全等三角形的判定与性质,以及相似三角形的判定与性质,熟练掌握各自的判定与性质是解本题的关键.
17. 可得到三组三角形相似;
先利用两组对应边的比相等且夹角对应相等的两个三角形相似证明∽,则,再利用有两组角对应相等的两个三角形相似证明∽,然后利用相似比和比例的性质求的值.
本题考查了相似三角形的判断:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.
18. 本试题主要是考查了平面几何中相似三角形的证明的求解。
利用已知中为等腰直角三角形,延长BA至E,延长AB至F,,结合相似三角形的判定定理得到结论。
19. 由于四边形ABCD是正方形,那么可知,,即,从而有,再结合,可证相似于,那么DF::CE,而,,易求CF.
20. 根据等腰三角形的性质,由,D是BC中点得到,易得,再证明,于是根据有两组角对应相等的两个三角形相似即可得到结论.
本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似也考查了等腰三角形的性质,证题的关键是挖掘题目的隐藏条件:对顶角相等.
21. 根据两组对应边的比相等且夹角对应相等的两个三角形相似进行求解;
根据,,即可得出,进而得到;
先根据,,判定∽,即可得出,进而得到.
本题主要考查了相似三角形的判定与性质的运用,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合.
第14页,共14页
第13页,共14页
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
