12.2.2三角形全等的判定第二课时 “边角边”(SAS)判定 课件 (共27张PPT)
文档属性
| 名称 | 12.2.2三角形全等的判定第二课时 “边角边”(SAS)判定 课件 (共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 777.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-14 10:00:54 | ||
图片预览




文档简介
课件27张PPT。第十二章 全等三角形12.2 三角形全等的判定
第二课时 “边角边”(SAS)判定 进一步熟练尺规作图画等角的方法,并能根据SAS定理画出定三角形。
掌握全等三角形的“边角边”(SAS)判定定理,并能运用其解决问题。
通过探究过程,知道有两边和其中一边的对角分别相等的两个三角形不一定全等这一事实。什么是判定三角形全等的“边边边”定理?
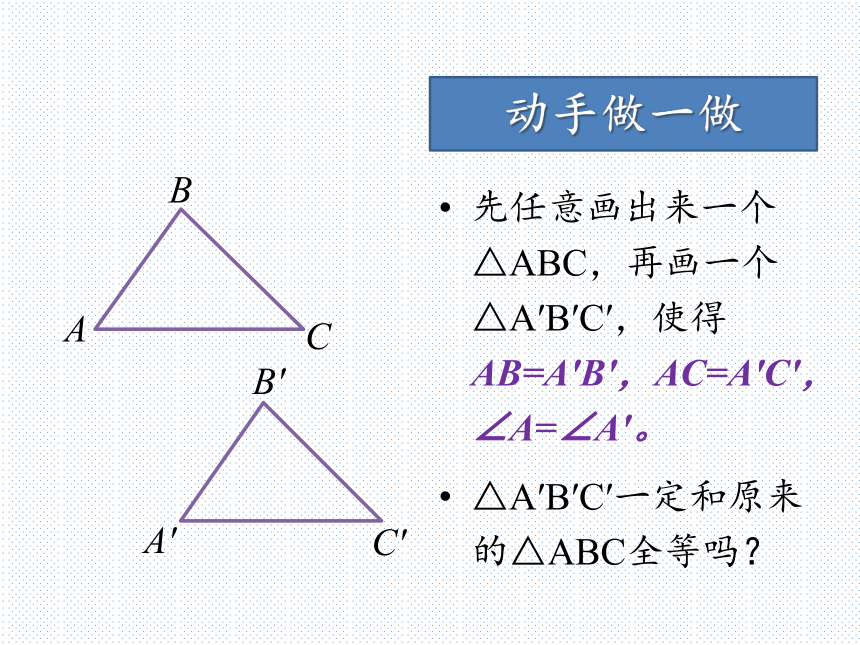
三条边都相等的三角形全等。动脑想一想动脑想一想如果只知道三角形的两条边分别相等,能不能判定两个三角形全等呢?如果再知道一个角相等,能不能判定两个三角形全等呢?动手做一做先任意画出来一个△ABC,再画一个△A′B′C′,使得AB=A′B′,AC=A′C′,∠A=∠A′。
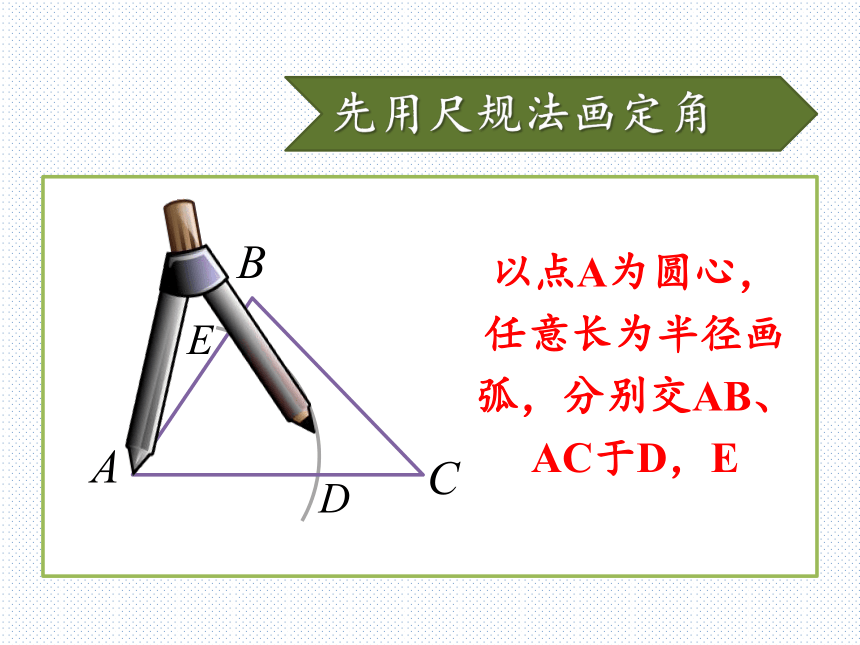
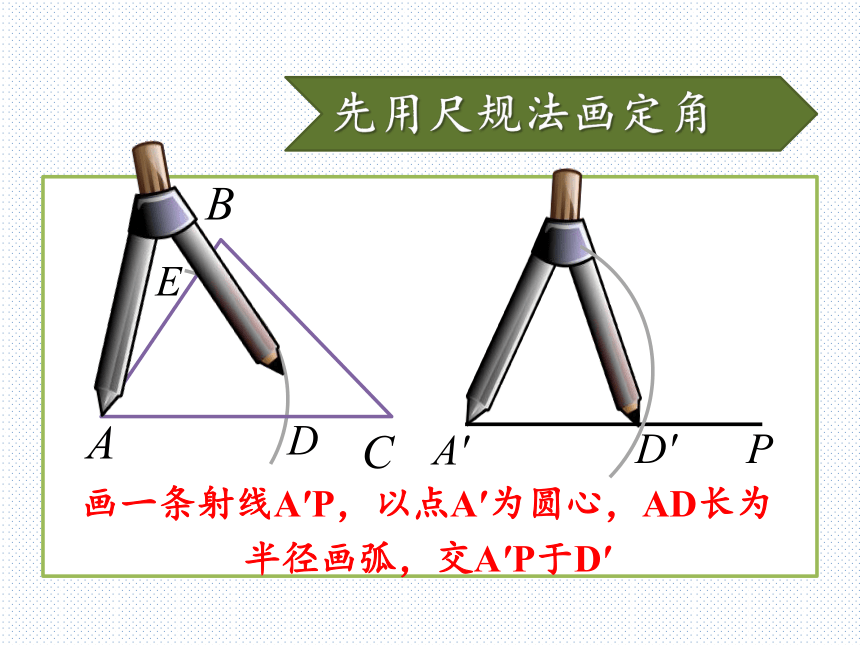
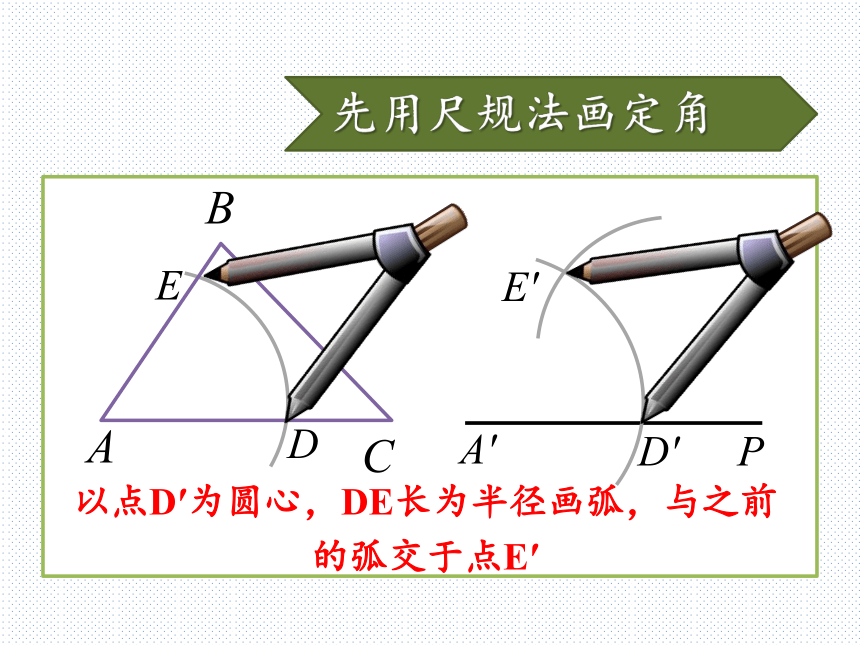
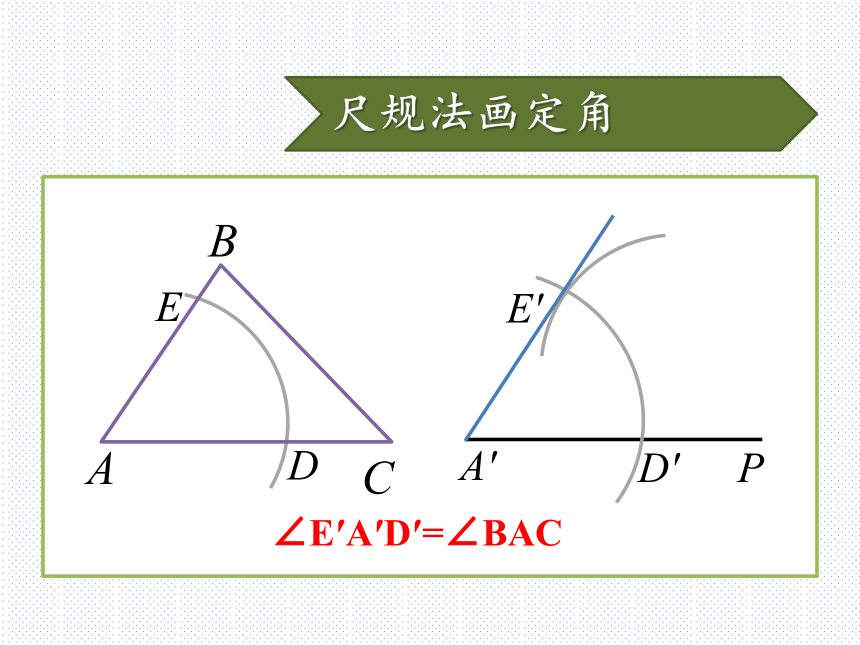
△A′B′C′一定和原来的△ABC全等吗?先用尺规法画定角以点A为圆心,任意长为半径画弧,分别交AB、AC于D,EED先用尺规法画定角D′ED画一条射线A′P,以点A′为圆心,AD长为半径画弧,交A′P于D′先用尺规法画定角A′PD′E′ED以点D′为圆心,DE长为半径画弧,与之前的弧交于点E′尺规法画定角∠E′A′D′=∠BACEDA′PD′E′接着画出三角形在射线A′P上截取AC=A′C′EDA′PD′E′C′接着画出三角形在射线A′E′上截取AB=A′B′EDA′PD′E′C′B′接着画出三角形连接△A′B′C′,大功告成!EDA′PD′E′C′B′“边边边”判定定理从刚才的尺规作图中,你能得到什么结论?
两边和它们的夹角分别相等的两个三角形全等。
(SAS,“边角边”)用这个定理,可以判定三角形全等!“边边边”判定定理∵在△ABC和△ DEF中
∴△ABC ≌△ DEF(SAS)动脑想一想如图,有一池塘,要测量池塘两端A,B的距离,可先在平地上取一点C,从C不经过池塘可直接到达点A和B。连接AC并延长到点D,使CD=CA。连接BC并延长到点E,使CE=CB。连接DE,那么测出DE的长度就是A,B的距离。为什么?动脑想一想在运用“边角边”定理判定三角形全等时,要注意:相等的角必须是相等的两边的夹角。
动脑想一想如果两个三角形的两边和其中一边的对角分别相等,能判定两个三角形全等吗?动手做一做把一长一短的两根木棍的一段固定在一起,摆出△ABC。固定住长木棍,转动段木棍,得到△ABD。
你发现了什么?不存在“边边角”定理!△ABC和△ABD满足AB=AB,AC=AD,∠B=∠B,但不全等。
有两边和其中一边的对角分别相等的两个三角形不一定全等!学完本节课你应该知道全等三角形“边角边”(SAS)判定数学语言
表示和证明定理:两边和它们的夹角分别相等的两个三角形全等不存在“边边角”定理!尺规作
定三角形动笔练一练如图,下列条件可以判定△ABD≌△CBD的是( )
AB=CB,∠ADB=∠CDB
AB=CB,∠A=∠C
AB=CB,∠ABD=∠CBD
AB=CD,∠ADB=∠CDBC动笔练一练如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,求证:∠A=∠D动笔练一练证明:
∵ BE=CF
∴ BE+EF=BF+EF,即BF=CE
在△ABF和△DCE中:
AB=DC
∠B=∠C
BF=CE
∴△ABF ≌△DCE(SAS)动笔练一练如图,已知AB=AC,AD=AE, 且∠BAC=∠DAE。试证明:△ABD≌△ACE。动笔练一练证明:
∵∠BAC=∠DAE,也即
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE
在△ABD与△ACE中:
AB=AC
∠BAD=∠CAE
AD=AE
∴△ABD ≌△ ACE(SSS)课后练一练请同学们独立完成配套课后练习题。下课!谢谢同学们!
第二课时 “边角边”(SAS)判定 进一步熟练尺规作图画等角的方法,并能根据SAS定理画出定三角形。
掌握全等三角形的“边角边”(SAS)判定定理,并能运用其解决问题。
通过探究过程,知道有两边和其中一边的对角分别相等的两个三角形不一定全等这一事实。什么是判定三角形全等的“边边边”定理?
三条边都相等的三角形全等。动脑想一想动脑想一想如果只知道三角形的两条边分别相等,能不能判定两个三角形全等呢?如果再知道一个角相等,能不能判定两个三角形全等呢?动手做一做先任意画出来一个△ABC,再画一个△A′B′C′,使得AB=A′B′,AC=A′C′,∠A=∠A′。
△A′B′C′一定和原来的△ABC全等吗?先用尺规法画定角以点A为圆心,任意长为半径画弧,分别交AB、AC于D,EED先用尺规法画定角D′ED画一条射线A′P,以点A′为圆心,AD长为半径画弧,交A′P于D′先用尺规法画定角A′PD′E′ED以点D′为圆心,DE长为半径画弧,与之前的弧交于点E′尺规法画定角∠E′A′D′=∠BACEDA′PD′E′接着画出三角形在射线A′P上截取AC=A′C′EDA′PD′E′C′接着画出三角形在射线A′E′上截取AB=A′B′EDA′PD′E′C′B′接着画出三角形连接△A′B′C′,大功告成!EDA′PD′E′C′B′“边边边”判定定理从刚才的尺规作图中,你能得到什么结论?
两边和它们的夹角分别相等的两个三角形全等。
(SAS,“边角边”)用这个定理,可以判定三角形全等!“边边边”判定定理∵在△ABC和△ DEF中
∴△ABC ≌△ DEF(SAS)动脑想一想如图,有一池塘,要测量池塘两端A,B的距离,可先在平地上取一点C,从C不经过池塘可直接到达点A和B。连接AC并延长到点D,使CD=CA。连接BC并延长到点E,使CE=CB。连接DE,那么测出DE的长度就是A,B的距离。为什么?动脑想一想在运用“边角边”定理判定三角形全等时,要注意:相等的角必须是相等的两边的夹角。
动脑想一想如果两个三角形的两边和其中一边的对角分别相等,能判定两个三角形全等吗?动手做一做把一长一短的两根木棍的一段固定在一起,摆出△ABC。固定住长木棍,转动段木棍,得到△ABD。
你发现了什么?不存在“边边角”定理!△ABC和△ABD满足AB=AB,AC=AD,∠B=∠B,但不全等。
有两边和其中一边的对角分别相等的两个三角形不一定全等!学完本节课你应该知道全等三角形“边角边”(SAS)判定数学语言
表示和证明定理:两边和它们的夹角分别相等的两个三角形全等不存在“边边角”定理!尺规作
定三角形动笔练一练如图,下列条件可以判定△ABD≌△CBD的是( )
AB=CB,∠ADB=∠CDB
AB=CB,∠A=∠C
AB=CB,∠ABD=∠CBD
AB=CD,∠ADB=∠CDBC动笔练一练如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,求证:∠A=∠D动笔练一练证明:
∵ BE=CF
∴ BE+EF=BF+EF,即BF=CE
在△ABF和△DCE中:
AB=DC
∠B=∠C
BF=CE
∴△ABF ≌△DCE(SAS)动笔练一练如图,已知AB=AC,AD=AE, 且∠BAC=∠DAE。试证明:△ABD≌△ACE。动笔练一练证明:
∵∠BAC=∠DAE,也即
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE
在△ABD与△ACE中:
AB=AC
∠BAD=∠CAE
AD=AE
∴△ABD ≌△ ACE(SSS)课后练一练请同学们独立完成配套课后练习题。下课!谢谢同学们!
