2.1 认识无理数课时作业

2.1 认识无理数课时作业
姓名：__________班级：__________考号：__________
一 、选择题
1.在﹣1.414，π，3.，3.1212212221…（两个1之间的2依次增加1个），0这些数中无理数的个数为（　　）
A．5 B．2 C．3 D．4
2.下列说法中，错误的个数是（ ）①实数可以分为有理数和无理数，也可以分为正实数和负实数；②不是分数；③无限小数必是无理数；④两个无理数之积是无理数A．1 B．2 C．3 D．4
3.在0，3.14159，，，，中，无理数的个数是（ ）A．1个 B．2个 C．3个 D．4个
4.下列四个实数中，是无理数的为（　　）
A． 0 B． ﹣3 C． D．
5.下列各数是无理数的是（　　）
A．0B．﹣1C． D．
6.如图，正方形网格中，每小格正方形边长为1，则网格上的三角形ABC中，边长为无理数的边数有（　　）
A．0条 B．1条 C．2条 D．3条
7.一个长方形的长与宽分别是6、3，它的对角线的长可能是（　　）
A．整数 B．分数 C．有理数 D．无理数
8.如图，数轴上点A，B分别对应1，2，过点B作PQ⊥AB，以点B为圆心，AB长为半径画弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，则点M对应的数是（　　）
A． B． C． D．
二 、填空题
9.在实数、、中，无理数是．
10.在实数π，，，，，0.2121121112…（每两个2之间依次多一个1）中，无理数共有?????个．
11.写出一个同时满足下列条件的无理数：①它在数轴上表示的点在原点的左边；?②它的绝对值小于2．答：????．
12.点A．B、C在格点图中的位置如图5所示，格点小正方形的边长为1，则点C到线段AB所在直线的距离是　 　．
13.如图，O为数轴原点，A，B两点分别对应﹣3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为　　　　　　．
14.如图，正方形网格每个小正方形的边长为1，则网格上△ABC的三条边中，边长是无理数的有　 　条．
15.已知Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，根据下列条件判断第三边是否是有理数，
（1）a=2，b=3，c　 　有理数；
（2）a=5，b=12，c　 　有理数．
三 、解答题
16.下列各数中哪些是有理数，哪些是无理数？
0.0213，，||，e=2.71828…，﹣3.1415926，，．
17.设面积为5π的圆的半径为y，请回答下列问题：
（1）y是有理数吗？请说明你的理由；
（2）估计y的值（结果精确到十分位），并用计算器验证你的估计．
18.在△ABC中，AB=AC，AD是底边上的高，如图，若AC=6cm，AD=5cm，求BD的值．（精确到0.01cm）
19.已知实数x，y满足关系式+|y2﹣1|=0．
（1）求x，y的值；
（2）判断是有理数还是无理数？并说明理由．
20.如图，已知△ABC中，∠B=90 o，AB=8cm，BC=6cm，P、Q分别为AB、BC边上的动点，点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始B→C方向运动，且速度为每秒2cm，它们同时出发；设出发的时间为t秒．
（1）出发2秒后，求PQ的长；
（2）从出发几秒钟后，△PQB能形成等腰三角形？
（3）在运动过程中，直线PQ能否把原三角形周长分成相等的两部分？若能够，请求出运动时间；若不能够，请说明理由．
21.在如图所示的正方形网格里，以格点为顶点按要求画图，并回答问题．
（1）画一个面积是9的正方形，它的边长是有理数还是无理数？为什么？
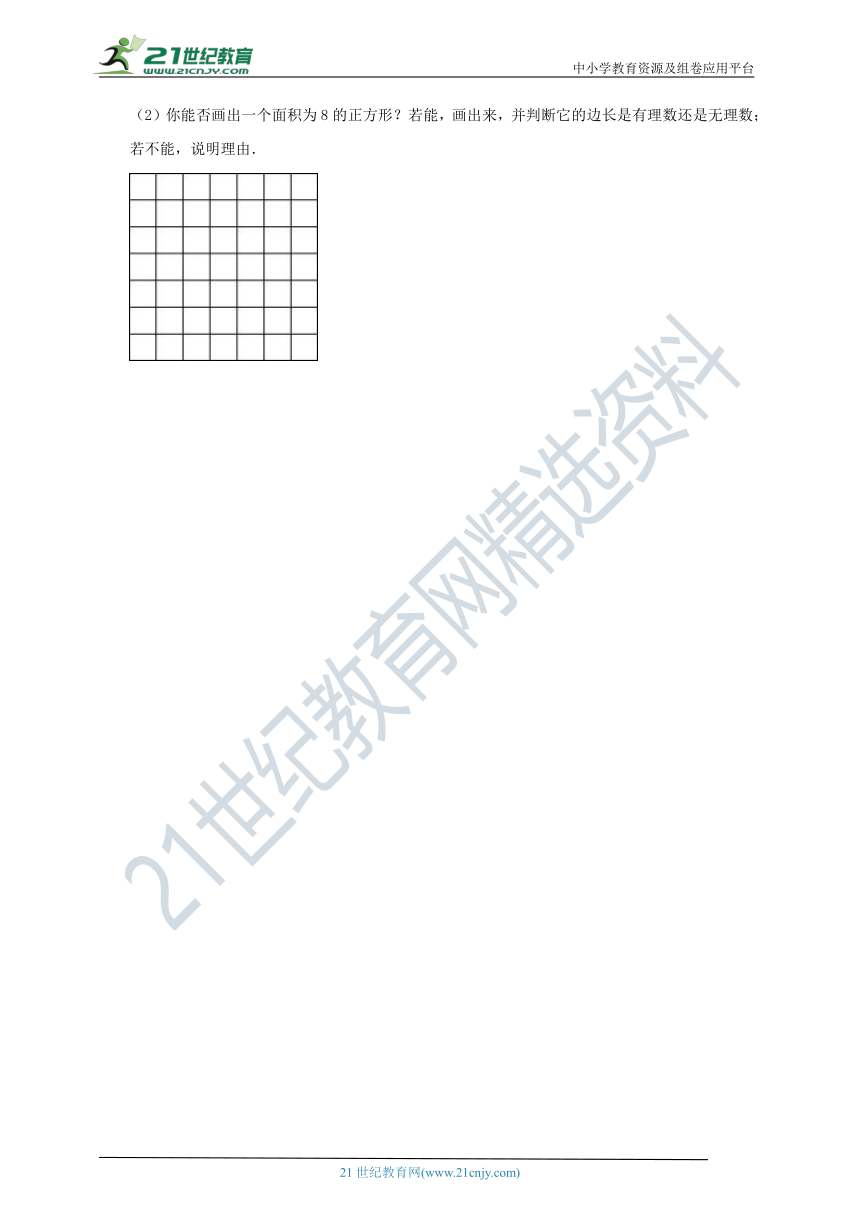
（2）你能否画出一个面积为8的正方形？若能，画出来，并判断它的边长是有理数还是无理数；若不能，说明理由．
答案解析
一 、选择题
1.【考点】无理数．
【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
解：π，3.1212212221…（两个1之间的2依次增加1个）是无理数，
故选：B．
【点评】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
2.【分析】①根据实数的分类即可判定；②根据分数的定义和无理数的定义即可判定；③根据无理数的定义即可判定；④根据无理数的定义即可判定．解：①据实数的分类：实数可以分为有理数和无理数，也可分为正实数、负实数和0，故说法所以①错误；②根据分数的定义中分数中的分子或分母经过约分后不能出现无理数，否则就不是分数，不是分数是无理数，故说法②正确；③根据无限不循环小数称为无理数，无限小数不一定是无理数，故说法③错误；两个无理数相乘不一定是无理数，如×等于2是有理数，故说法④错误．有三个选项错误．故选C．
3.【分析】根据无理数的定义（无理数是指无限不循环小数）判断即可．解：理数有，，共2个，故选B．
4.解：A．0是整数，是有理数，故A选项错误；
B、﹣3是整数，是有理数，故B选项错误；
C、=2是无理数，故C选项正确；
D、是无限循环小数，是有理数，故D选项错误．
故选：C．
点评： 此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
5.【考点】无理数．
【分析】根据无理数是无限不循环小数，可得答案．
【解答】解：0，﹣1，是有理数，是无理数，
故选：C．
【点评】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，，0.8080080008…（每两个8之间依次多1个0）等形式．
6.【考点】勾股定理．
【分析】根据图中所示，利用勾股定理求出每个边长，然后根据无理数的定义即可得出答案．
解：观察图形，应用勾股定理，得
AB=，
BC==，
AC==5，
∴AB和BC两个边长都是无理数．
故选：C．
【点评】此题考查了勾股定理的应用．注意格点三角形的三边的求解方法：借助于直角三角形，用勾股定理求解．
7.【考点】勾股定理．
【分析】长方形的长、宽和对角线，构成一个直角三角形，可用勾股定理，求得对角线的长，再进行选择即可．
解：∵ ==3，
∴对角线长是无理数．
故选D．
【点评】本题考查了长方形性质及勾股定理的应用，考查了利用勾股定理解直角三角形的能力以及实数的分类．
8.【考点】勾股定理；实数与数轴．
【分析】直接利用勾股定理得出OC的长，进而得出答案．
【解答】解：如图所示：连接OC，
由题意可得：OB=2，BC=1，
则AC==，
故点M对应的数是：．
故选：B．
二 、填空题
9.考点： 无理数．
分析： 根据无理数的三种形式求解．
解：=2，
无理数有：．
故答案为：．
点评： 本题考查了无理数的知识，解答本题的关键是掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数．
10.【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．解：无理数有：π，-1，-，0.2121121112…（每两个2之间依次多一个1），共有4个．故答案是：4．
11.【分析】根据条件所写的无理数是绝对值小于2的负无理数，答案不唯一．解：无理数有：-．故答案是：-．
12.【考点】勾股定理．
【分析】连接AC，BC，设点C到线段AB所在直线的距离是h，利用勾股定理求出AB的长，利用三角形的面积公式即可得出结论．
解：连接AC，BC，设点C到线段AB所在直线的距离是h，
∵S△ABC=3×3﹣×2×1﹣×2×1﹣×3×3﹣1=9﹣1﹣1﹣﹣1=，AB==，
∴×h=，
∴h=．
故答案为：．
13.【考点】勾股定理；实数与数轴；等腰三角形的性质．
【分析】先利用等腰三角形的性质得到OC⊥AB，则利用勾股定理可计算出OC=，然后利用画法可得到OM=OC=，于是可确定点M对应的数．
【解答】解：∵△ABC为等腰三角形，OA=OB=3，
∴OC⊥AB，
在Rt△OBC中，OC===，
∵以O为圆心，CO长为半径画弧交数轴于点M，
∴OM=OC=，
∴点M对应的数为．
故答案为．
14.【考点】无理数；勾股定理
【分析】根据图中所示，利用勾股定理求出每个边长，然后根据无理数的定义即可得出答案．
解：根据题意得：
AC==5，
AB==，
BC==，
所以边长为无理数的边数有2条．
故答案为：2．
【点评】此题考查了勾股定理的应用．要注意格点三角形的三边的求解方法：借助于直角三角形，用勾股定理求解．
15.【考点】无理数；勾股定理
【分析】（1）已知两直角边求斜边，利用勾股定理求得c，再根据有理数的定义即可求解；
（2）已知两直角边求斜边，利用勾股定理求得c，再根据有理数的定义即可求解．
解：∵Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，
∴（1）a=2，b=3，c==，c不是有理数；
（2）a=5，b=12，c==13，c是有理数．
故答案为：不是，是．
【点评】本题考查了利用勾股定理解直角三角形的运算能力．勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
三 、解答题
16.【考点】有理数；无理数
【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可得到答案．
解：0.0213是小数，=和||=是分数、﹣3.1415926是小数、是循环小数都是有理数，
、e=2.71828…是无限不循环小数、是无限不循环小数它们都是无理数．
【点评】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
17.【考点】近似数和有效数字；无理数；估算无理数的大小；解一元二次方程﹣直接开平方法
【分析】（1）先根据圆的面积公式列出方程，求出y的值，再根据有理数、无理数的定义进行判断；
（2）根据精确度的定义，将（1）中求出的y的值进行估计，并用计算器验证即可．
解：（1）y不是有理数．
理由如下：
由题意，得πy2=5π，
∴y2=5，
∵y＞0，
∴y=．
由于是无理数，所以y是无理数，即y不是有理数．
（2）∵2.12=4.41，2.22=4.84，2.32=5.29，
∴估计精确到十分位，约为2.2，
用计算器计算=2.23606…，
∴≈2.2（结果精确到十分位）．
【点评】本题主要考查了无理数的定义及估算无理数大小的方法．
无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．
估算无理数的大小要用逼近法，即用有理数逼近无理数，从而求出无理数的近似值．
18.【考点】勾股定理
【分析】先根据勾股定理求出CD的长，再由等腰三角形的性质即可得出结论．
解：∵AC=6cm，AD=5cm，AD⊥BC，
∴CD====≈3.32（cm）．
∵AB=AC，
∴BD=CD=3.32（cm）．
【点评】本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
19.【考点】非负数的性质：绝对值；非负数的性质：算术平方根；无理数
【分析】（1）根据非负数的和等于零，可得方程组，根据解方程组，可得答案；
（2）根据开平方，无理数是无限不循环小数，可得答案．
解：（1）由题意，得，
解得：；
（2）当x=2，y=1时，=，是无理数．
当x=2，y=﹣1时，==2，是有理数．
【点评】本题考查了非负数的性质，利用非负数的性质得出方程组是解题关键．
20.【考点】勾股定理
【分析】（1）我们求出BP、BQ的长，用勾股定理解决即可．（2）△PQB形成等腰三角形，即BP=BQ，我们可设时间为t，列出方程2t=8-1×t，解方程即得结果．（3）直线PQ把原三角形周长分成相等的两部分，根据勾股定理可知AC=10cm，即三角形的周长为24cm，则有BP+BQ=12，即2t+（8-1×t）=12，解方程即可
解：（1）出发2秒后，BP=6，BQ=4，PQ=；
（2）设时间为t，列方程得
2t=8-1×t，
解得t=；
（3）根据勾股定理可知AC=10cm，即三角形的周长为24cm，则有BP+BQ=12，
设时间为t，列方程得
2t+（8-1×t）=12，
解得t=4，
当t=4时，点Q运动的路程是4×2=8＞6，
所以不能够．
点评：本题重点考查了利用勾股定理解决问题的能力，综合性较强．
21.【考点】无理数；勾股定理
【分析】（1）画一个边长为=3的正方形，再根据有理数的定义判断即可；
（2）画一个边长为=2，即直角边为2的等腰直角三角形的斜边长为边长的正方形，再根据有理数的定义判断即可．
解：（1）如图1，画一个边长为=3的正方形，它的边长是有理数；
（2）画一个边长为=2的正方形，它的边长是无理数．
【点评】考查了格点正方形的画法．本题需仔细分析题意，结合图形，利用勾股定理和正方形的性质即可解决问题．