12.2.1三角形全等的判定 第一课时 “边边边”(SSS)判定(共31张PPT)
文档属性
| 名称 | 12.2.1三角形全等的判定 第一课时 “边边边”(SSS)判定(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 721.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-15 00:00:00 | ||
图片预览




文档简介
课件31张PPT。第十二章 全等三角形12.2 三角形全等的判定
第一课时 “边边边”(SSS)判定 了解判定两个三角形全等时,至少要知道三组条件这一原理。
掌握全等三角形的“边边边”(SSS)判定定理,并能运用其解决问题。
能用尺规作图根据已知三角形画出另一全等三角形,并能作一角等于已知角。什么是全等三角形?
能够完全重合的两个三角形叫做全等三角形。
全等三角形具有哪些性质?
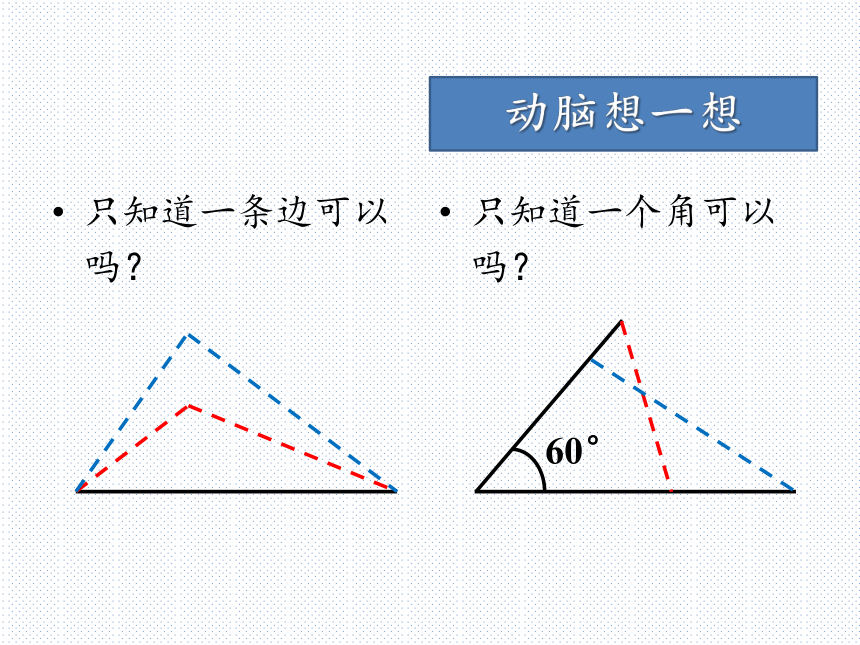
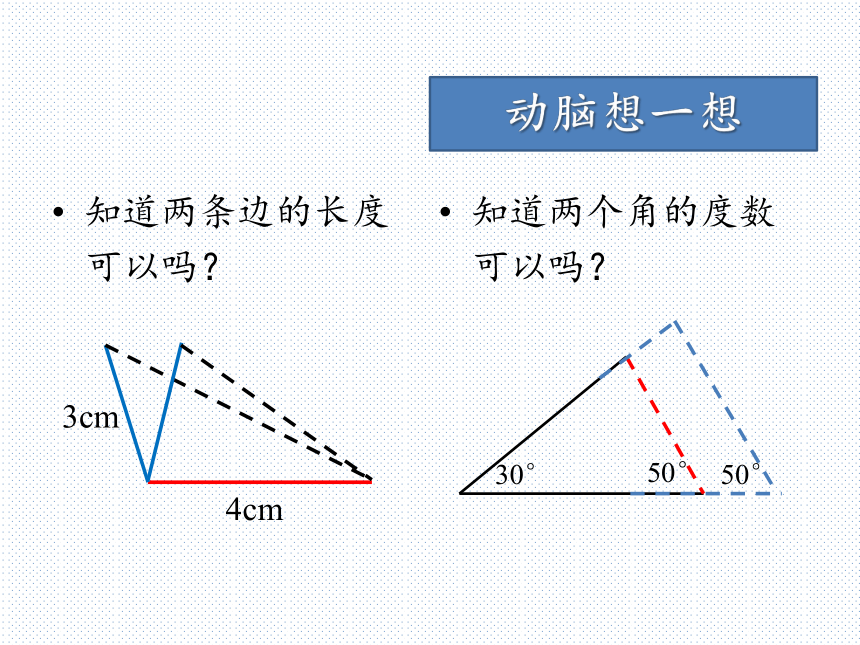
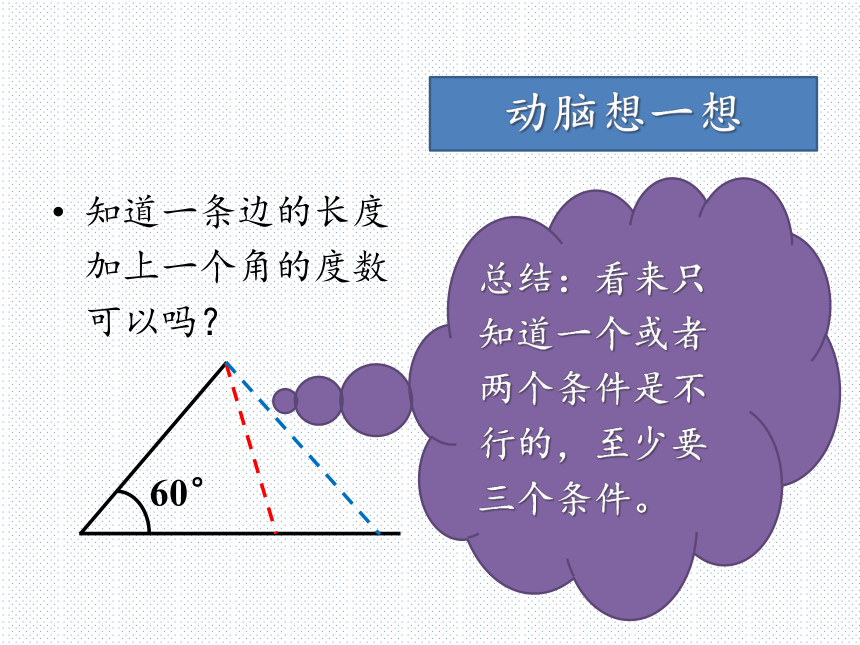
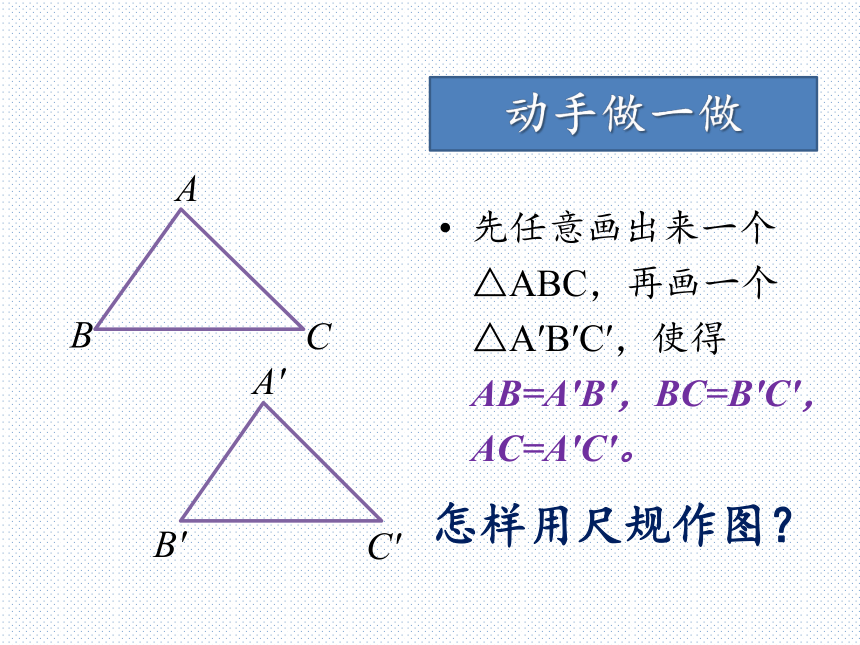
全等三角形的对应边相等,对应角也相等。动脑想一想动脑想一想实验室一块三角形玻璃仪器不小心被小明打碎了,老师让小明重去配一块一模一样的,小明该知道哪些条件才能配出来一模一样的玻璃仪器呢?只知道一个角可以吗?动脑想一想只知道一条边可以吗?知道两个角的度数可以吗?动脑想一想知道两条边的长度可以吗?总结:看来只知道一个或者两个条件是不行的,至少要三个条件。动脑想一想知道一条边的长度加上一个角的度数可以吗?动手做一做先任意画出来一个△ABC,再画一个△A′B′C′,使得AB=A′B′,BC=B′C′,AC=A′C′。
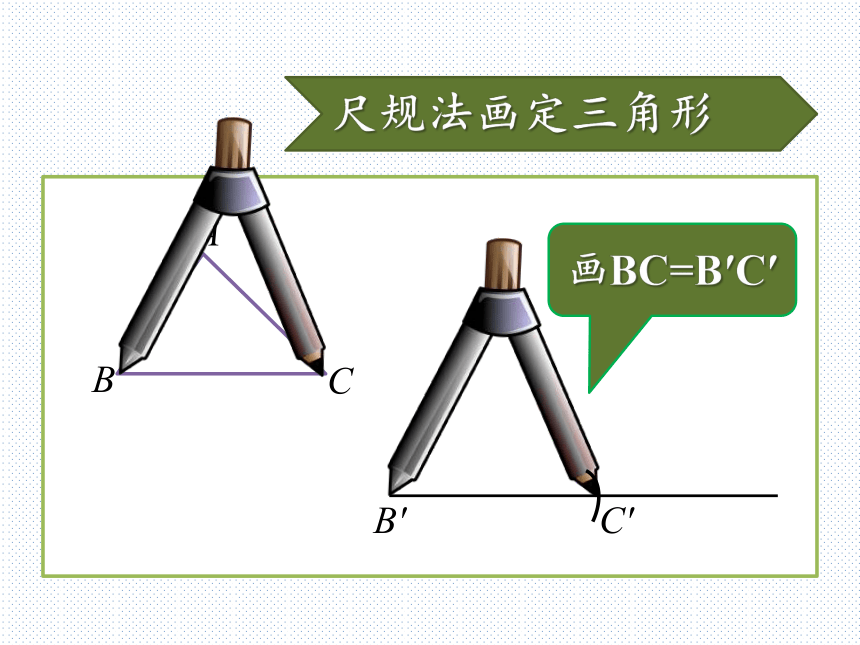
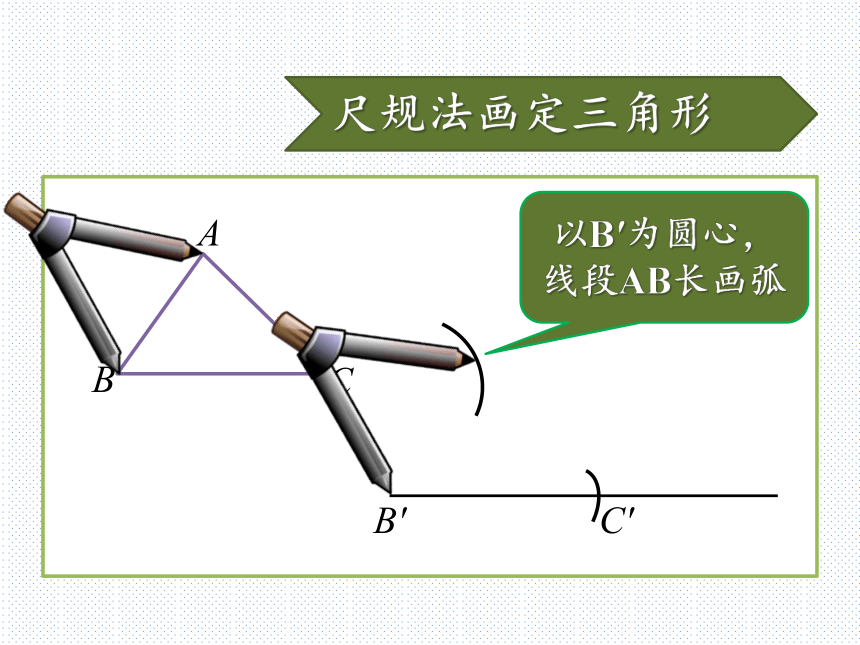
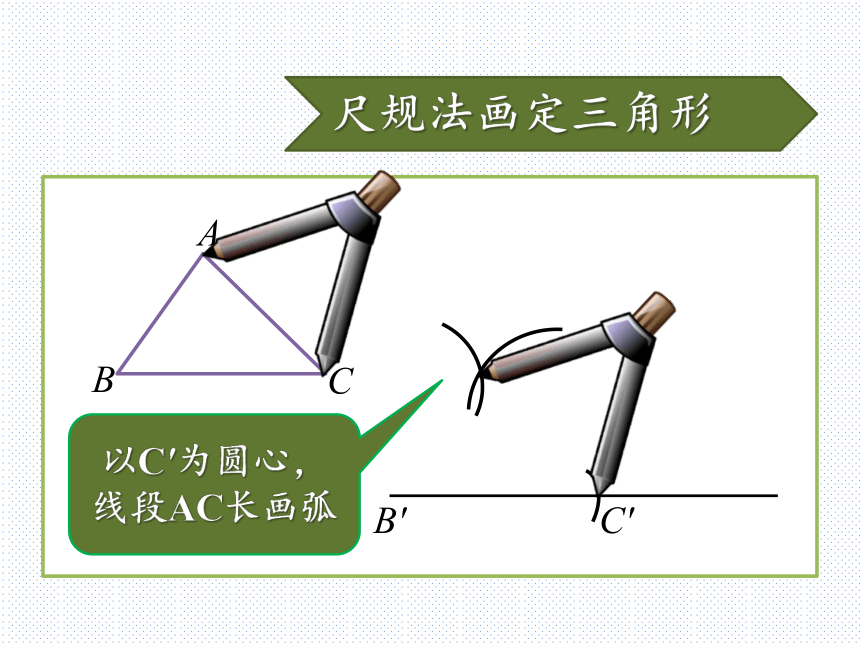
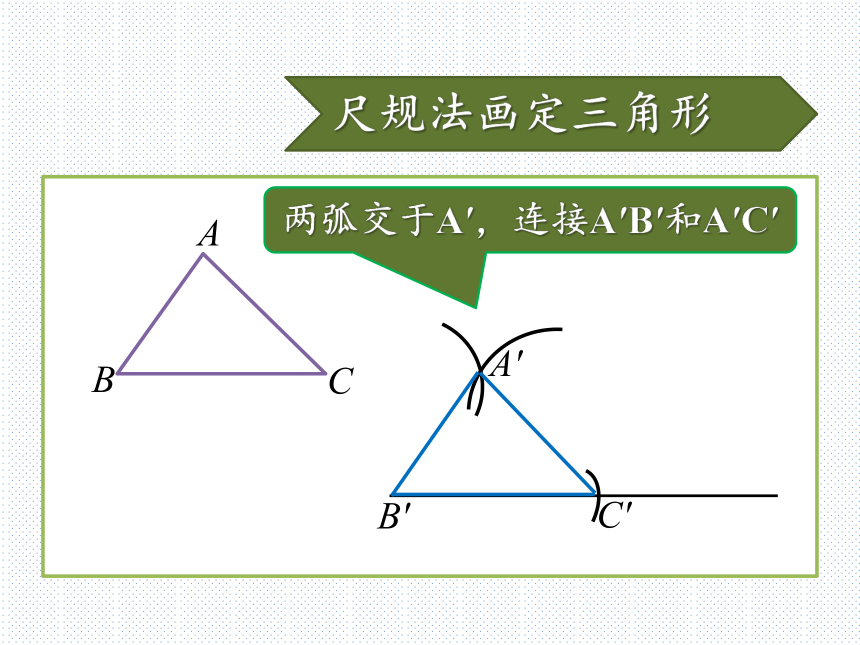
怎样用尺规作图?尺规法画定三角形B′C′画BC=B′C′尺规法画定三角形B′C′以B′为圆心,线段AB长画弧尺规法画定三角形B′C′以C′为圆心,线段AC长画弧尺规法画定三角形B′C′两弧交于A′,连接A′B′和A′C′A′“边边边”判定定理从刚才的尺规作图中,你能得到什么结论?
三边分别相等的两个三角形全等。(SSS,“边边边”)用这个定理,可以判定三角形全等!“边边边”判定定理∵在△ABC和△ DEF中
∴△ABC ≌△ DEF(SSS)“边边边”判定定理判断两个三角形全等的推理过程,叫做证明三角形全等。
证明三角形全等时,总共分三步:
首先指明全等的两个三角形(对应好顶点)
然后把三个条件写出,并用大括号括起来
最后下结论,后面给出判定定理的简称动脑想一想在如图的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架,求证△ABD≌△ACD。动脑想一想动手做一做已知:∠AOB
求作:∠A′O′B′,使得∠A′O′B′=∠AOB
怎样用尺规作一个角等于已知角?尺规法画定角以点O为圆心,任意长为半径画弧,分别交OA、OB于C,DDC尺规法画定角DCO′A′画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于C′C′尺规法画定角DCO′A′以点C′为圆心,CD长为半径画弧,与之前的弧交于点D′C′D′尺规法画定角DCO′A′C′D′B′∠A′O′B′=∠AOB想一想,为什么刚才就可以画出两个相等的角呢?动脑想一想显然:OC=O′C′,CD=C′D′
并且OC=OD,O′C′=O′D′
也即OD=O′D′,边边边全等学完本节课你应该知道全等三角形
“边边边”
判定数学语言表示和证明定理:三条边都相等的三角形全等尺规画定三角形尺规作图尺规画等角动笔练一练满足下列条件的两个三角形不一定全等的是( )
有一边相等的两个等边三角形
有一腰和底边对应相等的两个等腰三角形
周长相等的两个三角形
三条边都相等的三角形C动笔练一练已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB,求证:△ABC ≌△ FDE动笔练一练证明:
∵ DB是AB与DF的公共部分,且AD=BF
∴ AD+DB=BF+DB,即AB=DF
在△ABC和△FDE中:
AC=FE
BC=DE
AB=FD
∴△ABC ≌△ FDE(SSS)动笔练一练在四边形ABCD中,已知:AB=CD,AD=CB。试证明:∠A=∠C。动笔练一练证明:
在△ABC和△FDE中:
AB=CD(已知)
AD=CB(已知)
BD=DB(公共边)
∴△ABD ≌△ ACD(SSS)
∴∠A=∠C(全等三角形的对应角相等)课后练一练请同学们独立完成配套课后练习题。下课!谢谢同学们!
第一课时 “边边边”(SSS)判定 了解判定两个三角形全等时,至少要知道三组条件这一原理。
掌握全等三角形的“边边边”(SSS)判定定理,并能运用其解决问题。
能用尺规作图根据已知三角形画出另一全等三角形,并能作一角等于已知角。什么是全等三角形?
能够完全重合的两个三角形叫做全等三角形。
全等三角形具有哪些性质?
全等三角形的对应边相等,对应角也相等。动脑想一想动脑想一想实验室一块三角形玻璃仪器不小心被小明打碎了,老师让小明重去配一块一模一样的,小明该知道哪些条件才能配出来一模一样的玻璃仪器呢?只知道一个角可以吗?动脑想一想只知道一条边可以吗?知道两个角的度数可以吗?动脑想一想知道两条边的长度可以吗?总结:看来只知道一个或者两个条件是不行的,至少要三个条件。动脑想一想知道一条边的长度加上一个角的度数可以吗?动手做一做先任意画出来一个△ABC,再画一个△A′B′C′,使得AB=A′B′,BC=B′C′,AC=A′C′。
怎样用尺规作图?尺规法画定三角形B′C′画BC=B′C′尺规法画定三角形B′C′以B′为圆心,线段AB长画弧尺规法画定三角形B′C′以C′为圆心,线段AC长画弧尺规法画定三角形B′C′两弧交于A′,连接A′B′和A′C′A′“边边边”判定定理从刚才的尺规作图中,你能得到什么结论?
三边分别相等的两个三角形全等。(SSS,“边边边”)用这个定理,可以判定三角形全等!“边边边”判定定理∵在△ABC和△ DEF中
∴△ABC ≌△ DEF(SSS)“边边边”判定定理判断两个三角形全等的推理过程,叫做证明三角形全等。
证明三角形全等时,总共分三步:
首先指明全等的两个三角形(对应好顶点)
然后把三个条件写出,并用大括号括起来
最后下结论,后面给出判定定理的简称动脑想一想在如图的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架,求证△ABD≌△ACD。动脑想一想动手做一做已知:∠AOB
求作:∠A′O′B′,使得∠A′O′B′=∠AOB
怎样用尺规作一个角等于已知角?尺规法画定角以点O为圆心,任意长为半径画弧,分别交OA、OB于C,DDC尺规法画定角DCO′A′画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于C′C′尺规法画定角DCO′A′以点C′为圆心,CD长为半径画弧,与之前的弧交于点D′C′D′尺规法画定角DCO′A′C′D′B′∠A′O′B′=∠AOB想一想,为什么刚才就可以画出两个相等的角呢?动脑想一想显然:OC=O′C′,CD=C′D′
并且OC=OD,O′C′=O′D′
也即OD=O′D′,边边边全等学完本节课你应该知道全等三角形
“边边边”
判定数学语言表示和证明定理:三条边都相等的三角形全等尺规画定三角形尺规作图尺规画等角动笔练一练满足下列条件的两个三角形不一定全等的是( )
有一边相等的两个等边三角形
有一腰和底边对应相等的两个等腰三角形
周长相等的两个三角形
三条边都相等的三角形C动笔练一练已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB,求证:△ABC ≌△ FDE动笔练一练证明:
∵ DB是AB与DF的公共部分,且AD=BF
∴ AD+DB=BF+DB,即AB=DF
在△ABC和△FDE中:
AC=FE
BC=DE
AB=FD
∴△ABC ≌△ FDE(SSS)动笔练一练在四边形ABCD中,已知:AB=CD,AD=CB。试证明:∠A=∠C。动笔练一练证明:
在△ABC和△FDE中:
AB=CD(已知)
AD=CB(已知)
BD=DB(公共边)
∴△ABD ≌△ ACD(SSS)
∴∠A=∠C(全等三角形的对应角相等)课后练一练请同学们独立完成配套课后练习题。下课!谢谢同学们!
