《互斥事件》
图片预览







文档简介
【教学目标】理解互斥事件的概念,能从集
合角度理解事件关系,了解互斥事件的
概率加法公式,掌握利用概率的性质求
概率.
【教学重点】概率的加法公式及其应用.
【教学难点】事件的关系与运算.
1、古典概型:
(1)试验中所有可能出现的基本事件只有有限个;(有限性)
(2)每个基本事件出现的可能性相等.(等可能性)
这样两个特点的概率模型称为古典概率概型,简称古典概型.
2、古典概型计算任何事件的概率计算公式为:
3、求某个随机事件A包含的基本事件的个数和实验中基本事件的总数时常用的方法是列举法(画树状图和列表),注意做到不重不漏.
4、概率模型:
(1)抛掷骰子; (2)袋中无放回摸球;
(3)袋中有放回摸球
1. 鱼与熊掌不可兼得;
3. 考试中的单项选择题。
4. 掷骰子,向上的点数分别是
1、2、3、4、5、6.
不能同时发生!
2. 抽奖时,“中奖”和“不中奖” 。
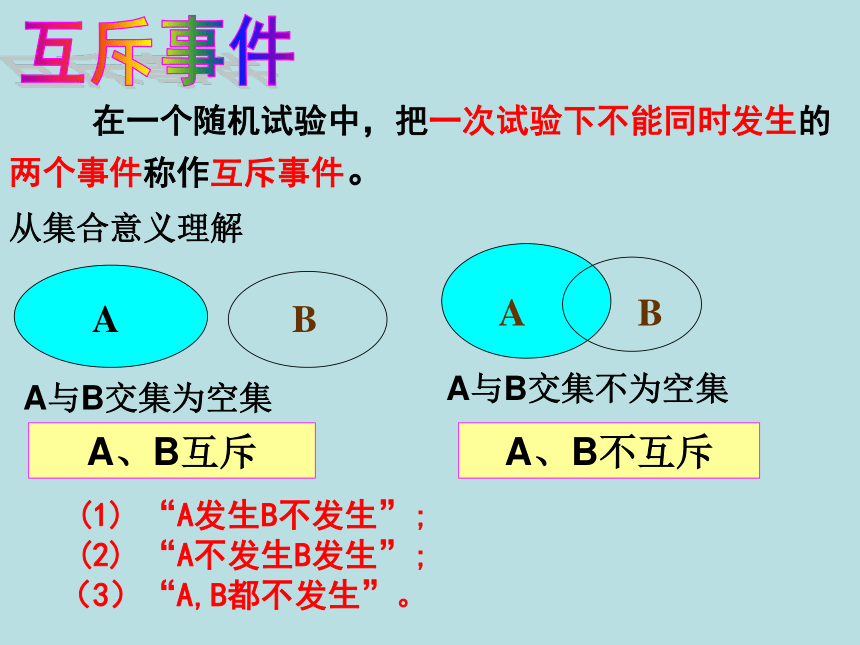
A、B互斥
A、B不互斥
从集合意义理解
在一个随机试验中,把一次试验下不能同时发生的两个事件称作互斥事件。
(1) “A发生B不发生”;
(2) “A不发生B发生”;
(3)“A,B都不发生”。
【如】
你还能举出一些生活
中的其他例子吗?
抛硬币,“正面朝上”和“反面朝上”
解 互斥事件: (1)(2)(3)
例1、在一个健身房里,用拉力器进行锻炼时,需要选取2个质量盘装在拉力器上.有2个装质量盘的箱子每个箱子中都装有4个不同的质量盘2.5 kg、5 kg、10 kg和20 kg,随机
地从2个箱子中各取1个质量盘,下面的事件A和事件B是否是互斥事件?
(1)事件A=“总质量为20 kg”,事件B=“总质量为30 kg”;
(2)事件A=“总质量为7.5 kg”,事件B=“总质量超过10 kg”;
(3)事件A=“总质量不超过10 kg”,
事件B=“总质量超过10 kg”;
(4)事件A=“总质量为20 kg”,事件B=“总质量超过10 kg” .
对于(4)中的事件A和事件B,随机地从2个箱子中各取1个质量盘,当总质量为20kg时,事件A与事件B同时发生,因此,事件A与事件B不是互斥事件.
给定事件A,B,规定A+B为一个事件,叫做A、B的和事件。事件A+B发生是指
(1) “A发生B不发生”;
(2) “A不发生B发生”;
(3) “A、B同时发生”.
在例1的(1)中,A表示事件“总质量为20kg”,B表示事件“总质量为30kg”我们把事件“总质量为20kg或30kg”记作A+B
事件A和事件B至少有一个发生.
【问题】例题中(2)(3)和(4)中的事件A和B,A+B各表示什么事件?
(2) A+B表示“总质量为7.5 kg或总质量超过10kg”;
(3)A+B表示“总质量不超过10 kg或总质量超过10
kg”, 即事件全体;
(4)A+B表示“总质量为20 kg或总质量超过10 kg”
即事件B .
(1)根据你的结果,你发现P(A+B)与P(A)+P(B)有什
么样的大小关系?
P(A+B)=P(A)+P(B)
1/16
1/8
3/16
3/16
1/8
3/4
7/8
7/8
1/4
3/4
1
1
互斥事件的概率求解
(1) (2) (3)
P(A)
P(B)
P(A)+P(B)
P(A+B)
在一个随机实验中,如果随机事件A和B是互斥事件,那么有
P(A+B)=P(A)+P(B).
(2)加法公式的前提条件是:事件A与B互斥.如果没有这一条件,加法公式将不能应用.
【说明】
(1)互斥事件的概率等于互斥事件分别发生的概率之和, 这就是概率的加法公式,也称互斥事件的概率的加法公式.
P(A1+A2+ ? ? ? +An)=P(A1)+P(A2)+ ? ? ? +P(An)
2、一般地,如果随机事件A1、A2、 ? ? ? 、An
中任意两个是互斥事件,那么有
1、事件A1、A2、…、An中至少有一个发生
表示事件A1+A2+ …+An发生.
彼此互斥事件
【解】(1)事件D即事件A+C,
因为事件A=“抽到的是一等品”和事件C=“抽到的
是三等品”是互斥事件,
由互斥事件的概率加法公式得:
P(D)=P(A+C)=P(A)+P(C)=0.7+0.05=0.75.
(2)事件E即事件B+C,因为事件B=“抽到的是二等品”和事件C=“抽到的是三等品”是互斥事件,由互斥事件的概率加法公式,
P(E)=P(B+C)=P(B)+P(C)=0.1+0.05=0.15.
【点评】容易看出,事件D+E表示“抽到的产品是一等品或二等品或三等品” .事件D和事件E不是互斥事件,因此不满足互斥事件的概率加法公式.
事实上,P(D+E)=P(A)+P(B)+P(C)=0.85,而
P(D)+P(E)=[P(A)+P(C)]+[P(B)+P(C)]=0.9,
“抽到的是三等品”的概率P(C)在P(D)和P(E)中各算了一次,因此,事件D+E的概率P(D+E)不等于P(D)+P(E).
例3、某地政府准备对当地的农村产业结构进行调整,为此政府进行了一次民意调查.100个人接受了调查,他们被要求在赞成调整、反对调整、对这次调整不发表看法中任选一项.调查结果如表所示:
随机选取一个被调查者,他对这次调整表示反对或不发表看法的概率是多少?
男 女 总计
赞成 18 9 27
反对 12 25 37
不发表看法 20 16 36
总计 50 50 100
【解】用A表示事件“对这次调整表示反对”,B表示
事件“对这次调整不发表看法”,则A和B是互斥
事件,并且A+B就表示事件“对这次调整表示反
对或不发表看法”,由互斥事件的概率加法公式,
因此,随机选取的一个被调查者对这次调整表示反对或不发表看法的概率是0.73.
例4、在例1中,随机地从2个箱子中各取1个质量盘,如果一个人不能拉动超过22kg的质量,那么他将不能拉开拉力器,则他不能拉开拉力器的概率是多少?
【解】总质量超过22kg,即质量为22.5kg,25kg, 30kg,40kg.
用A2表示事件“总质量为25kg”,
用A3表示事件“总质量为30kg”,
用A4表示事件“总质量为40kg”,
用A1表示事件“总质量为22.5kg”,
则A1+A2+A3+A4就表示事件“总质量超过22kg”.
P(A1+A2+A3+A4 ) = P(A1)+P(A2)+P(A3)+P(A4)
= + + +
2
16
2
16
2
16
1
16
?0.44.
因此,随机地从2个箱子中各取1个质量盘,此人不能拉开拉力器的概率约为0.44.
而A1,A2,A3,A4中任意两个是互斥事件,由互斥事件的概率加法公式,随机地从2个箱子中各取1个质量盘,总质量超过22kg的概率为:
1.互斥事件:不可能同时发生的两个事件叫做互斥事件。
若事件A与B互斥,则P(A+B)=P(A)+P(B).
若事件A1,A2,…,An彼此互斥,则
P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
求随机事件A的概率的常用方法
先将事件A转化成n个彼此互斥的事件A1,A2,…,An之和,再由P(A1+A2+…+An)= P(A1)+P(A2)+…+P(An).
互斥事件的判断
例1 从6件正品与3件次品中任取3件,观察正品件数与次品件数,判断下列每对事件是不是互斥事件;如果是,再判断它们是不是对立事件.
(1)“恰好有1件次品”和“恰好有2件次品;
(2)“至少有1件次品”和“全是次品”;
(3)“至少有2件次品”和“至多有1件次品.
问题分析:从6件正品与3件次品中任取3件,共有4种情况:
①3件全是正品; (3全正)
②2件正品1件次品; (2正1次)
③1件正品2件次品; (1正2次)
④全是次品. (3全次)
例1 从6件正品与3件次品中任取3件,观察正品件数与次品件数,判断下列每对事件是不是互斥事件;如果是,再判断它们是不是对立事件.
4种情况:
①3全正;②2正1次;③1正2次;④3全次。
(1)“恰好有1件次品”和“恰好有2件次品;
互斥
(2)“至少有1件次品”和“全是次品”;
不互斥
(3)“至少有2件次品”和“至多有1件次品.
互斥
【提炼升华】
判断是否为互斥事件的关键是看两个事件能否同时发生;两个事件为对立事件的前提是两事件互斥,且必有一个事件发生.具体应用时,可把试验结果写出来,看所求事件包含哪几个试验结果,从而判断所给两事件之间的关系.
合角度理解事件关系,了解互斥事件的
概率加法公式,掌握利用概率的性质求
概率.
【教学重点】概率的加法公式及其应用.
【教学难点】事件的关系与运算.
1、古典概型:
(1)试验中所有可能出现的基本事件只有有限个;(有限性)
(2)每个基本事件出现的可能性相等.(等可能性)
这样两个特点的概率模型称为古典概率概型,简称古典概型.
2、古典概型计算任何事件的概率计算公式为:
3、求某个随机事件A包含的基本事件的个数和实验中基本事件的总数时常用的方法是列举法(画树状图和列表),注意做到不重不漏.
4、概率模型:
(1)抛掷骰子; (2)袋中无放回摸球;
(3)袋中有放回摸球
1. 鱼与熊掌不可兼得;
3. 考试中的单项选择题。
4. 掷骰子,向上的点数分别是
1、2、3、4、5、6.
不能同时发生!
2. 抽奖时,“中奖”和“不中奖” 。
A、B互斥
A、B不互斥
从集合意义理解
在一个随机试验中,把一次试验下不能同时发生的两个事件称作互斥事件。
(1) “A发生B不发生”;
(2) “A不发生B发生”;
(3)“A,B都不发生”。
【如】
你还能举出一些生活
中的其他例子吗?
抛硬币,“正面朝上”和“反面朝上”
解 互斥事件: (1)(2)(3)
例1、在一个健身房里,用拉力器进行锻炼时,需要选取2个质量盘装在拉力器上.有2个装质量盘的箱子每个箱子中都装有4个不同的质量盘2.5 kg、5 kg、10 kg和20 kg,随机
地从2个箱子中各取1个质量盘,下面的事件A和事件B是否是互斥事件?
(1)事件A=“总质量为20 kg”,事件B=“总质量为30 kg”;
(2)事件A=“总质量为7.5 kg”,事件B=“总质量超过10 kg”;
(3)事件A=“总质量不超过10 kg”,
事件B=“总质量超过10 kg”;
(4)事件A=“总质量为20 kg”,事件B=“总质量超过10 kg” .
对于(4)中的事件A和事件B,随机地从2个箱子中各取1个质量盘,当总质量为20kg时,事件A与事件B同时发生,因此,事件A与事件B不是互斥事件.
给定事件A,B,规定A+B为一个事件,叫做A、B的和事件。事件A+B发生是指
(1) “A发生B不发生”;
(2) “A不发生B发生”;
(3) “A、B同时发生”.
在例1的(1)中,A表示事件“总质量为20kg”,B表示事件“总质量为30kg”我们把事件“总质量为20kg或30kg”记作A+B
事件A和事件B至少有一个发生.
【问题】例题中(2)(3)和(4)中的事件A和B,A+B各表示什么事件?
(2) A+B表示“总质量为7.5 kg或总质量超过10kg”;
(3)A+B表示“总质量不超过10 kg或总质量超过10
kg”, 即事件全体;
(4)A+B表示“总质量为20 kg或总质量超过10 kg”
即事件B .
(1)根据你的结果,你发现P(A+B)与P(A)+P(B)有什
么样的大小关系?
P(A+B)=P(A)+P(B)
1/16
1/8
3/16
3/16
1/8
3/4
7/8
7/8
1/4
3/4
1
1
互斥事件的概率求解
(1) (2) (3)
P(A)
P(B)
P(A)+P(B)
P(A+B)
在一个随机实验中,如果随机事件A和B是互斥事件,那么有
P(A+B)=P(A)+P(B).
(2)加法公式的前提条件是:事件A与B互斥.如果没有这一条件,加法公式将不能应用.
【说明】
(1)互斥事件的概率等于互斥事件分别发生的概率之和, 这就是概率的加法公式,也称互斥事件的概率的加法公式.
P(A1+A2+ ? ? ? +An)=P(A1)+P(A2)+ ? ? ? +P(An)
2、一般地,如果随机事件A1、A2、 ? ? ? 、An
中任意两个是互斥事件,那么有
1、事件A1、A2、…、An中至少有一个发生
表示事件A1+A2+ …+An发生.
彼此互斥事件
【解】(1)事件D即事件A+C,
因为事件A=“抽到的是一等品”和事件C=“抽到的
是三等品”是互斥事件,
由互斥事件的概率加法公式得:
P(D)=P(A+C)=P(A)+P(C)=0.7+0.05=0.75.
(2)事件E即事件B+C,因为事件B=“抽到的是二等品”和事件C=“抽到的是三等品”是互斥事件,由互斥事件的概率加法公式,
P(E)=P(B+C)=P(B)+P(C)=0.1+0.05=0.15.
【点评】容易看出,事件D+E表示“抽到的产品是一等品或二等品或三等品” .事件D和事件E不是互斥事件,因此不满足互斥事件的概率加法公式.
事实上,P(D+E)=P(A)+P(B)+P(C)=0.85,而
P(D)+P(E)=[P(A)+P(C)]+[P(B)+P(C)]=0.9,
“抽到的是三等品”的概率P(C)在P(D)和P(E)中各算了一次,因此,事件D+E的概率P(D+E)不等于P(D)+P(E).
例3、某地政府准备对当地的农村产业结构进行调整,为此政府进行了一次民意调查.100个人接受了调查,他们被要求在赞成调整、反对调整、对这次调整不发表看法中任选一项.调查结果如表所示:
随机选取一个被调查者,他对这次调整表示反对或不发表看法的概率是多少?
男 女 总计
赞成 18 9 27
反对 12 25 37
不发表看法 20 16 36
总计 50 50 100
【解】用A表示事件“对这次调整表示反对”,B表示
事件“对这次调整不发表看法”,则A和B是互斥
事件,并且A+B就表示事件“对这次调整表示反
对或不发表看法”,由互斥事件的概率加法公式,
因此,随机选取的一个被调查者对这次调整表示反对或不发表看法的概率是0.73.
例4、在例1中,随机地从2个箱子中各取1个质量盘,如果一个人不能拉动超过22kg的质量,那么他将不能拉开拉力器,则他不能拉开拉力器的概率是多少?
【解】总质量超过22kg,即质量为22.5kg,25kg, 30kg,40kg.
用A2表示事件“总质量为25kg”,
用A3表示事件“总质量为30kg”,
用A4表示事件“总质量为40kg”,
用A1表示事件“总质量为22.5kg”,
则A1+A2+A3+A4就表示事件“总质量超过22kg”.
P(A1+A2+A3+A4 ) = P(A1)+P(A2)+P(A3)+P(A4)
= + + +
2
16
2
16
2
16
1
16
?0.44.
因此,随机地从2个箱子中各取1个质量盘,此人不能拉开拉力器的概率约为0.44.
而A1,A2,A3,A4中任意两个是互斥事件,由互斥事件的概率加法公式,随机地从2个箱子中各取1个质量盘,总质量超过22kg的概率为:
1.互斥事件:不可能同时发生的两个事件叫做互斥事件。
若事件A与B互斥,则P(A+B)=P(A)+P(B).
若事件A1,A2,…,An彼此互斥,则
P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
求随机事件A的概率的常用方法
先将事件A转化成n个彼此互斥的事件A1,A2,…,An之和,再由P(A1+A2+…+An)= P(A1)+P(A2)+…+P(An).
互斥事件的判断
例1 从6件正品与3件次品中任取3件,观察正品件数与次品件数,判断下列每对事件是不是互斥事件;如果是,再判断它们是不是对立事件.
(1)“恰好有1件次品”和“恰好有2件次品;
(2)“至少有1件次品”和“全是次品”;
(3)“至少有2件次品”和“至多有1件次品.
问题分析:从6件正品与3件次品中任取3件,共有4种情况:
①3件全是正品; (3全正)
②2件正品1件次品; (2正1次)
③1件正品2件次品; (1正2次)
④全是次品. (3全次)
例1 从6件正品与3件次品中任取3件,观察正品件数与次品件数,判断下列每对事件是不是互斥事件;如果是,再判断它们是不是对立事件.
4种情况:
①3全正;②2正1次;③1正2次;④3全次。
(1)“恰好有1件次品”和“恰好有2件次品;
互斥
(2)“至少有1件次品”和“全是次品”;
不互斥
(3)“至少有2件次品”和“至多有1件次品.
互斥
【提炼升华】
判断是否为互斥事件的关键是看两个事件能否同时发生;两个事件为对立事件的前提是两事件互斥,且必有一个事件发生.具体应用时,可把试验结果写出来,看所求事件包含哪几个试验结果,从而判断所给两事件之间的关系.
