带电粒子在匀强磁场中的运动
文档属性
| 名称 | 带电粒子在匀强磁场中的运动 |  | |
| 格式 | rar | ||
| 文件大小 | 25.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2010-08-24 16:20:00 | ||
图片预览






文档简介
课件21张PPT。带电粒子在匀强磁场中的运动------有界磁场中的动态分析带电粒子在匀强磁场中的运动(2)V⊥B-------匀速圆周运动(1)V//B-------匀速直线运动课前导学
质疑讨论一、粒子速度方向不变,速度大小变化 粒子运动轨迹的圆心都在垂直于初速度的直线上,速度增加时,轨道半径随着增加,寻找运动轨迹的临界点质疑讨论 此时由于速度大小不变,则所有粒子运动的轨道半径相同,但不同粒子的圆心位置不同,其共同规律是:所有粒子的圆心都在以入射点为圆心,以轨道半径为半径的圆上,从而找出动圆的圆心轨迹,再确定运动轨迹的临界点。二、粒子速度大小不变,速度方向变化
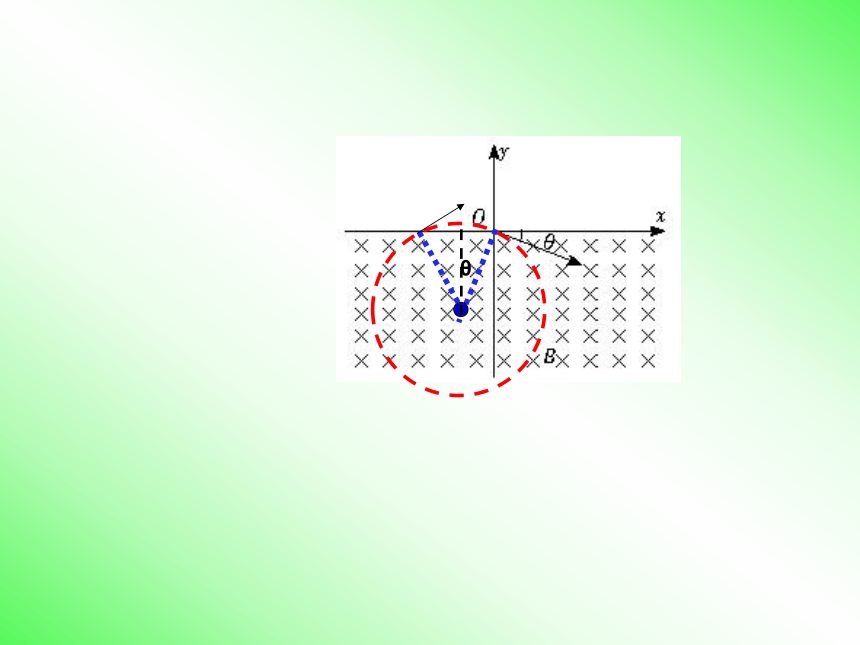
(1)圆心的确定:(2)半径的确定:(3)运动时间的确定:质疑讨论三、如何确定带电粒子圆周运动圆心、半径 和运动时间反馈矫正 问题1. 如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸里,磁感应强度为B.一带负电的粒子(质量为m、电荷量为q)以速度v0从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.求:
(1)该粒子射出磁场的位置;
(2)该粒子在磁场中运动的时间.(粒子所受重力不计)
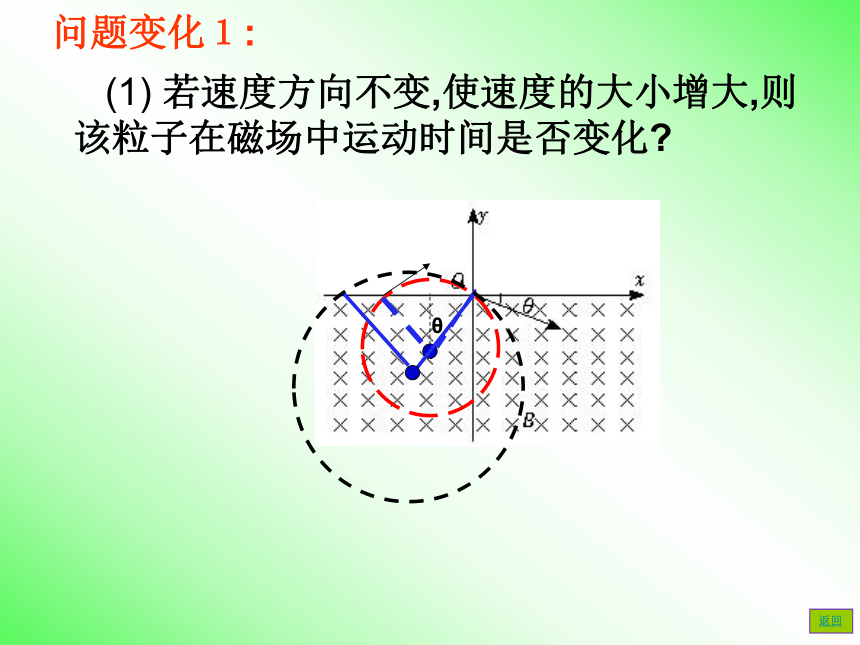
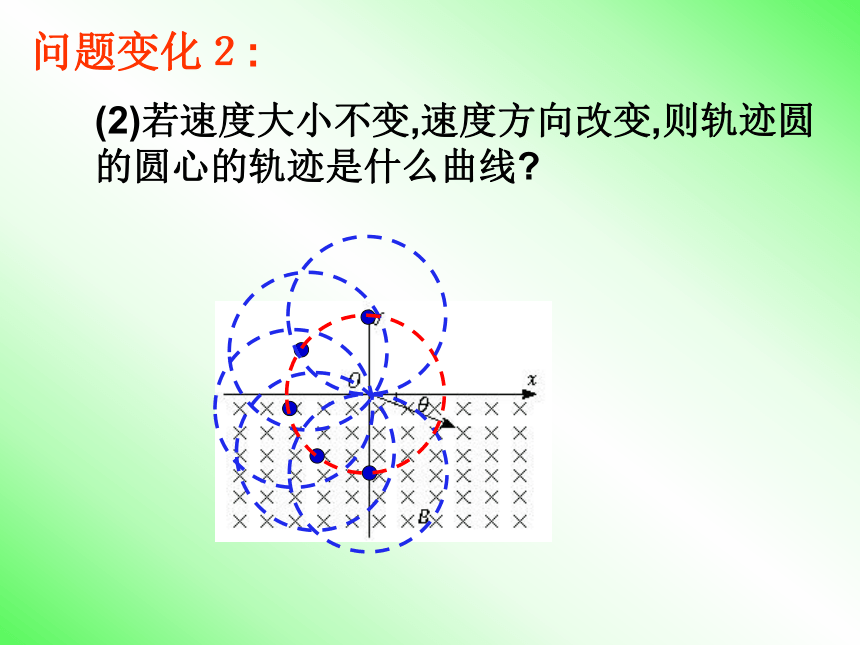
θ返回问题变化1: (1) 若速度方向不变,使速度的大小增大,则该粒子在磁场中运动时间是否变化?问题变化2:(2)若速度大小不变,速度方向改变,则轨迹圆的圆心的轨迹是什么曲线?问题变化3: 若磁场的下边界为y=L则为使粒子
能从磁场下边界射出,则v0 至少多大?问题2.
长为l 的水平极板间有如图所示的匀强磁场,磁感强度为B,板间距离也为l 。现有一质量为 m 、带电量为 +q 的粒子从左边板间中点处沿垂直于磁场的方向以速度 v0射入磁场,不计重力。要想使粒子不打在极板上,则粒子进入磁场时的速度 v0 应满足什么条件? ∴ v0 < q B l / 4 m
或 v0 > 5 q B l / 4 m解:若刚好从a 点射出,如图:R- l/2Rr=mv1/qB=l/4∴ v1=qBl /4m 若刚好从b 点射出,如图:要想使粒子不打在极板上, ∴ v2=5qBl /4mR2 = l 2 + ( R- l/2)2R= 5l /4= mv2/qB 返回O 问题3.在真空中半径为r=3cm的圆形区域内有一匀强磁场,B=0.2T ,方向如图示,一带正电的粒子以速度v=1.2×106m/s 的初速度从磁场边界上的直径ab一端的a点射入磁场,已知该粒子的荷质比q/m=108 C/kg,不计粒子重力,则粒子在磁场中运动的最长时间为 多少? 返回
分析:V以不同方向入射,以ab为弦的圆弧θ最大,时间最长. 圆周运动的半径∴ θ =30°T=2πR/v∴ t=T/6=5.2×10-8 sR=mv/qB
= 10-8 × 1.2×106÷0.2
= 0.06m返回巩固迁移 如图所示,宽度d = 8cm的匀强磁场区域(aa’,bb’足够长)磁感应强度B = 0.332T,方向垂直纸面向里,在边界aa’上放一α粒子源S,可沿纸面向各个方向均匀射出初速率相同的α粒子,已知α粒子的质量m = 6.64×10-27kg,电量q = 3.2×10-19C,射出时初速v0 = 3.2×106m/s。求:
(1)α粒子从b端出射时的最远点P与中心点O距离PO
(2)α粒子从b’端出射时的最远点Q与中心点 O的距离QOa′ab′bdSOO 1.已知带电粒子经过轨迹圆上两点及其速度确定圆心 方法:过两点作速度的垂线,两垂线交点即为圆心。 ABVVO 2.已知带电粒子经过轨迹圆上两点及一点的速度,
确定圆心 方法:过已知速度的点作速度的垂线和两点连线的中垂线,
两垂线交点即为圆心。 ABV谢谢同学们合作
质疑讨论一、粒子速度方向不变,速度大小变化 粒子运动轨迹的圆心都在垂直于初速度的直线上,速度增加时,轨道半径随着增加,寻找运动轨迹的临界点质疑讨论 此时由于速度大小不变,则所有粒子运动的轨道半径相同,但不同粒子的圆心位置不同,其共同规律是:所有粒子的圆心都在以入射点为圆心,以轨道半径为半径的圆上,从而找出动圆的圆心轨迹,再确定运动轨迹的临界点。二、粒子速度大小不变,速度方向变化
(1)圆心的确定:(2)半径的确定:(3)运动时间的确定:质疑讨论三、如何确定带电粒子圆周运动圆心、半径 和运动时间反馈矫正 问题1. 如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸里,磁感应强度为B.一带负电的粒子(质量为m、电荷量为q)以速度v0从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.求:
(1)该粒子射出磁场的位置;
(2)该粒子在磁场中运动的时间.(粒子所受重力不计)
θ返回问题变化1: (1) 若速度方向不变,使速度的大小增大,则该粒子在磁场中运动时间是否变化?问题变化2:(2)若速度大小不变,速度方向改变,则轨迹圆的圆心的轨迹是什么曲线?问题变化3: 若磁场的下边界为y=L则为使粒子
能从磁场下边界射出,则v0 至少多大?问题2.
长为l 的水平极板间有如图所示的匀强磁场,磁感强度为B,板间距离也为l 。现有一质量为 m 、带电量为 +q 的粒子从左边板间中点处沿垂直于磁场的方向以速度 v0射入磁场,不计重力。要想使粒子不打在极板上,则粒子进入磁场时的速度 v0 应满足什么条件? ∴ v0 < q B l / 4 m
或 v0 > 5 q B l / 4 m解:若刚好从a 点射出,如图:R- l/2Rr=mv1/qB=l/4∴ v1=qBl /4m 若刚好从b 点射出,如图:要想使粒子不打在极板上, ∴ v2=5qBl /4mR2 = l 2 + ( R- l/2)2R= 5l /4= mv2/qB 返回O 问题3.在真空中半径为r=3cm的圆形区域内有一匀强磁场,B=0.2T ,方向如图示,一带正电的粒子以速度v=1.2×106m/s 的初速度从磁场边界上的直径ab一端的a点射入磁场,已知该粒子的荷质比q/m=108 C/kg,不计粒子重力,则粒子在磁场中运动的最长时间为 多少? 返回
分析:V以不同方向入射,以ab为弦的圆弧θ最大,时间最长. 圆周运动的半径∴ θ =30°T=2πR/v∴ t=T/6=5.2×10-8 sR=mv/qB
= 10-8 × 1.2×106÷0.2
= 0.06m返回巩固迁移 如图所示,宽度d = 8cm的匀强磁场区域(aa’,bb’足够长)磁感应强度B = 0.332T,方向垂直纸面向里,在边界aa’上放一α粒子源S,可沿纸面向各个方向均匀射出初速率相同的α粒子,已知α粒子的质量m = 6.64×10-27kg,电量q = 3.2×10-19C,射出时初速v0 = 3.2×106m/s。求:
(1)α粒子从b端出射时的最远点P与中心点O距离PO
(2)α粒子从b’端出射时的最远点Q与中心点 O的距离QOa′ab′bdSOO 1.已知带电粒子经过轨迹圆上两点及其速度确定圆心 方法:过两点作速度的垂线,两垂线交点即为圆心。 ABVVO 2.已知带电粒子经过轨迹圆上两点及一点的速度,
确定圆心 方法:过已知速度的点作速度的垂线和两点连线的中垂线,
两垂线交点即为圆心。 ABV谢谢同学们合作
