数学五年级上苏教版2.6 简单组合图形的面积课件(共25张PPT)
文档属性
| 名称 | 数学五年级上苏教版2.6 简单组合图形的面积课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-16 07:05:43 | ||
图片预览



文档简介
(共25张PPT)
第2单元 多边形的面积
6 简单组合图形的面积
学习目标
2.能灵活应用不同方法计算同一个组合图形的面积,体会转化思想,感受解决问题的多样性,培养数学学习的兴趣。
1.巩固基本图形的面积计算,能根据基本图形的面积用“割补”的方法正确计算出组合图形的面积。
3. 在学习的过程中体会数学思维的价值。
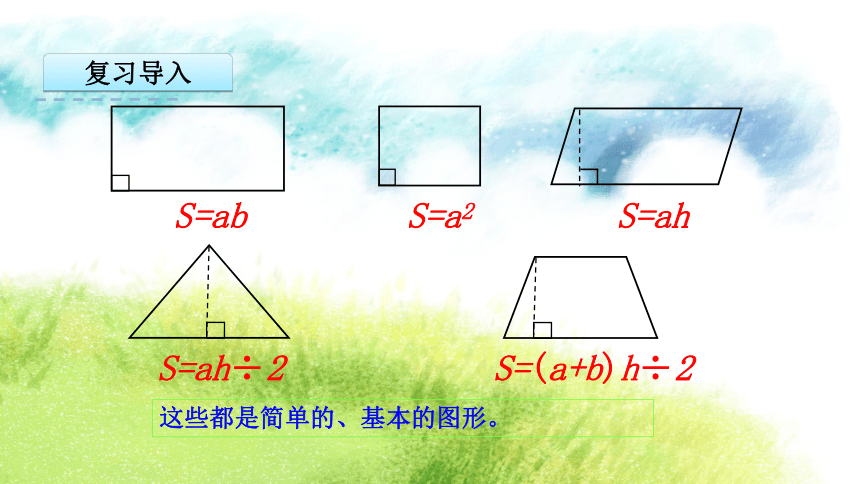
S=ab
S=a2
S=ah
S=ah÷2
S=(a+b)h÷2
这些都是简单的、基本的图形。
复习导入
像这样由几个基本图形拼成的图形,
我们就把它叫作组合图形。
复习导入
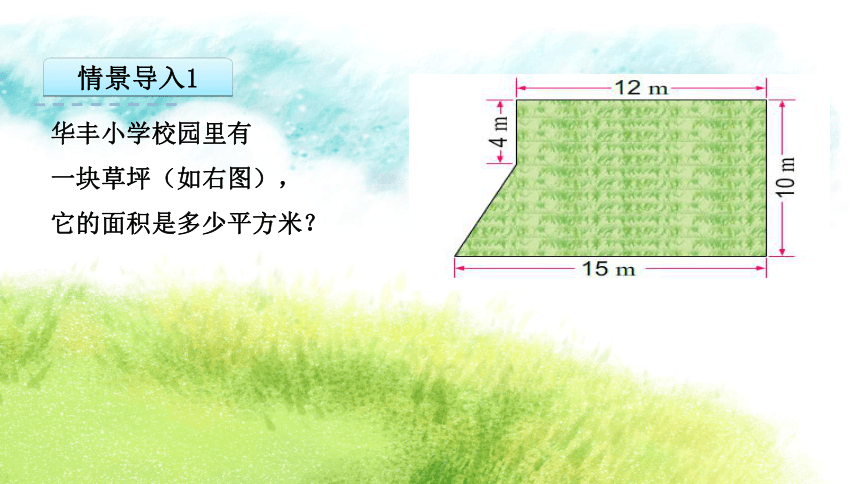
华丰小学校园里有
一块草坪(如右图),
它的面积是多少平方米?
情景导入1
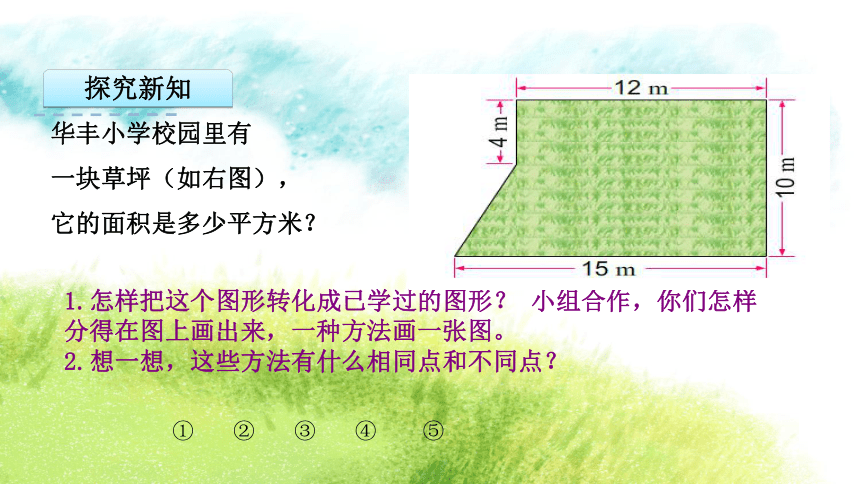
华丰小学校园里有
一块草坪(如右图),
它的面积是多少平方米?
1.怎样把这个图形转化成已学过的图形? 小组合作,你们怎样分得在图上画出来,一种方法画一张图。
2.想一想,这些方法有什么相同点和不同点?
探究新知
①
②
③
④
⑤
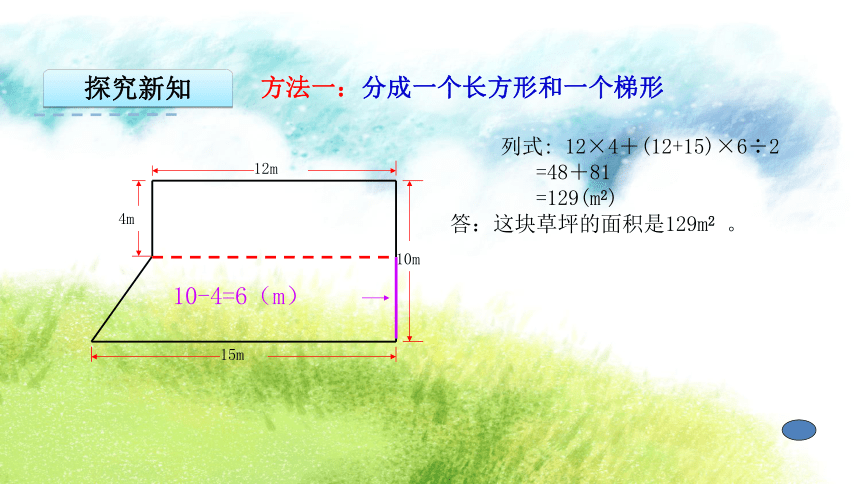
方法一:分成一个长方形和一个梯形
列式: 12×4+(12+15)×6÷2
=48+81
=129(m2)
答:这块草坪的面积是129m2 。
12m
10m
15m
4m
10-4=6(m)
探究新知
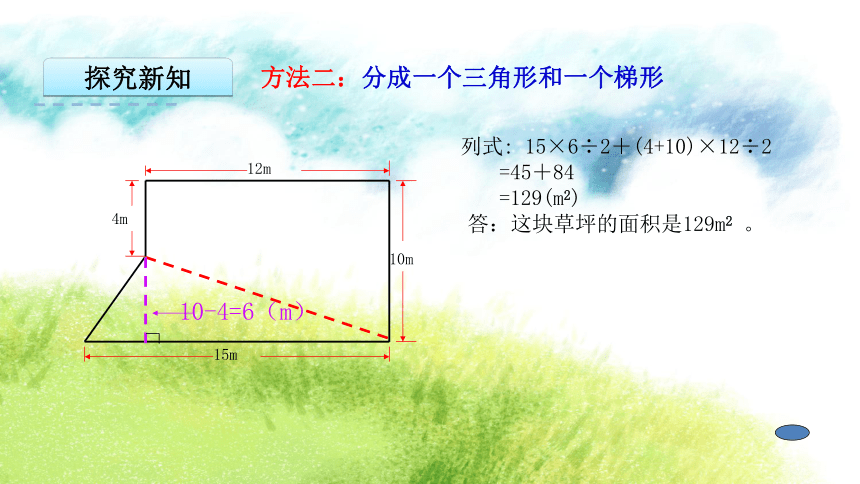
方法二:分成一个三角形和一个梯形
列式: 15×6÷2+(4+10)×12÷2
=45+84
=129(m2)
答:这块草坪的面积是129m2 。
12m
10m
15m
4m
10-4=6(m)
探究新知
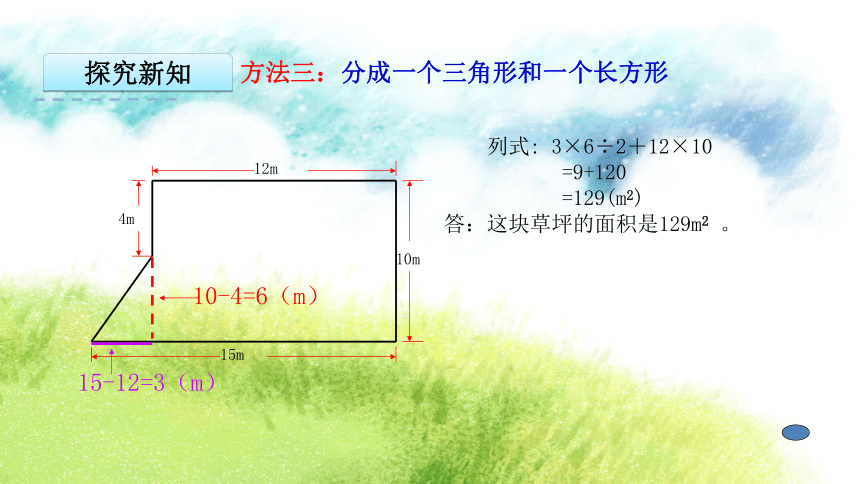
方法三:分成一个三角形和一个长方形
列式: 3×6÷2+12×10
=9+120
=129(m2)
答:这块草坪的面积是129m2 。
12m
10m
15m
4m
10-4=6(m)
15-12=3(m)
探究新知
方法四:添补成一个长方形
列式: 15×10- (4+10)×3÷2
=150-21
=129(m2)
答:这块草坪的面积是129m2。
12m
10m
15m
4m
15-12=3(m)
探究新知
图形内:分割法 求和
图形外:添补法 求差
如图:校园里有一个花圃你能计算出它
的面积是多少平方米吗 (可以尝试着不同的方法)
5m
6m
2m
2m
典题精讲
怎样把这个图形转化成已学过的图形?
6 m
2 m
5 m
4 m
6 m
2 m
5 m
4 m
6 m
2 m
5m
4 m
6 m
2 m
5 m
4 m
分割法
添补法
方法一:分割成两个长方形
方法二:分割成一个长方形
和一个正方形
方法三:分割成两个梯形
方法四:补上一个小正方形,使它成为一个大长方形
典题精讲
6 m
2 m
5 m
4 m
6 m
2 m
5 m
4 m
6×2 + 4×3
= 12 + 12
= 24(m2)
4×5+2×2
= 20 + 4
= 24(m2)
方法一:分割成两个长方形
方法二:分割成一个长方形和一个正方形
5-2=3(m)
6-4=2(m)
答:至少要24平方米的地板。
答:至少要24平方米的地板。
找出对应条件计算
典题精讲
6 m
2 m
5 m
4 m
6 m
2 m
5 m
4 m
(3+5)×4÷2 + (2+6)×2÷2
= 8×4÷2 + 8×2÷2
= 24(m2)
6×5 —2×3
= 30—6
= 24(m2)
方法三:分割成两个梯形
方法四:补上一个小长方形,使它成
为一个大长方形
3m
2m
2m
3m
答:至少要24平方米的地板。
答:至少要24平方米的地板。
找出对应条件计算
典题精讲
计算组合图形的面积主要可以采用“分割” 与“添补”的方法进行计算。
通过刚才的学习,你认为应怎样计算组合
图形的面积?
典题精讲
S长方形:10×8=80(cm2)
S梯形:(6+10)×2÷2=16(cm2)
S组合图形:80+16=96(cm2)
错误解答
易错提醒
S长方形:10×8=80(cm2)
S梯形:(6+10)×2÷2=16(cm2)
S组合图形:80+16=96(cm2)
错误解答
易错提醒
错解分析:组合图形的面积应该是长方形的面积减梯形的面积。
S长方形:10×8=80(cm2)
S梯形:(6+10)×2÷2=16(cm2)
S组合图形:80-16=64(cm2)
S长方形:10×8=80(cm2)
S梯形:(6+10)×2÷2=16(cm2)
S组合图形:80+16=96(cm2)
错误解答
正确解答
易错提醒
45°
阴影三角形的底和高都是2cm
三角形面积:2×2÷2=2(cm2)
S=ah÷2
学以致用
可以看成由
三角形和正
方形组成。
正方形面积:5×5=25(cm2)
三角形面积:8×5÷2=20(m2)
阴影面积:25+20=45(m2)
S=a
S=ah÷2
学以致用
求下图阴影部分的面积
4
三角形面积:4×4÷2=8(cm2)
学以致用
已知下图中平行四边形的面积是240平方厘米,求阴影部分的面积。
平行四边形的底即梯形的下底:
梯形面积:(10+16)×15÷2
=15×26÷2=195(cm2)
S=(a+b)×h÷2
学以致用
240÷15=16(cm)
可以看成由三角形+小正方形-下长三角形。
正方形面积:
5×5=25(cm )
三角形的面积:
8×8÷2=32(cm )
25+32=57(cm )
长三角形的面积:
13×5÷2=32.5(cm )
阴影面积:
57-32.5=24.5(cm )
学以致用
课堂小结
2.添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。
怎样求组合图形的面积?
1.分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。
第2单元 多边形的面积
6 简单组合图形的面积
学习目标
2.能灵活应用不同方法计算同一个组合图形的面积,体会转化思想,感受解决问题的多样性,培养数学学习的兴趣。
1.巩固基本图形的面积计算,能根据基本图形的面积用“割补”的方法正确计算出组合图形的面积。
3. 在学习的过程中体会数学思维的价值。
S=ab
S=a2
S=ah
S=ah÷2
S=(a+b)h÷2
这些都是简单的、基本的图形。
复习导入
像这样由几个基本图形拼成的图形,
我们就把它叫作组合图形。
复习导入
华丰小学校园里有
一块草坪(如右图),
它的面积是多少平方米?
情景导入1
华丰小学校园里有
一块草坪(如右图),
它的面积是多少平方米?
1.怎样把这个图形转化成已学过的图形? 小组合作,你们怎样分得在图上画出来,一种方法画一张图。
2.想一想,这些方法有什么相同点和不同点?
探究新知
①
②
③
④
⑤
方法一:分成一个长方形和一个梯形
列式: 12×4+(12+15)×6÷2
=48+81
=129(m2)
答:这块草坪的面积是129m2 。
12m
10m
15m
4m
10-4=6(m)
探究新知
方法二:分成一个三角形和一个梯形
列式: 15×6÷2+(4+10)×12÷2
=45+84
=129(m2)
答:这块草坪的面积是129m2 。
12m
10m
15m
4m
10-4=6(m)
探究新知
方法三:分成一个三角形和一个长方形
列式: 3×6÷2+12×10
=9+120
=129(m2)
答:这块草坪的面积是129m2 。
12m
10m
15m
4m
10-4=6(m)
15-12=3(m)
探究新知
方法四:添补成一个长方形
列式: 15×10- (4+10)×3÷2
=150-21
=129(m2)
答:这块草坪的面积是129m2。
12m
10m
15m
4m
15-12=3(m)
探究新知
图形内:分割法 求和
图形外:添补法 求差
如图:校园里有一个花圃你能计算出它
的面积是多少平方米吗 (可以尝试着不同的方法)
5m
6m
2m
2m
典题精讲
怎样把这个图形转化成已学过的图形?
6 m
2 m
5 m
4 m
6 m
2 m
5 m
4 m
6 m
2 m
5m
4 m
6 m
2 m
5 m
4 m
分割法
添补法
方法一:分割成两个长方形
方法二:分割成一个长方形
和一个正方形
方法三:分割成两个梯形
方法四:补上一个小正方形,使它成为一个大长方形
典题精讲
6 m
2 m
5 m
4 m
6 m
2 m
5 m
4 m
6×2 + 4×3
= 12 + 12
= 24(m2)
4×5+2×2
= 20 + 4
= 24(m2)
方法一:分割成两个长方形
方法二:分割成一个长方形和一个正方形
5-2=3(m)
6-4=2(m)
答:至少要24平方米的地板。
答:至少要24平方米的地板。
找出对应条件计算
典题精讲
6 m
2 m
5 m
4 m
6 m
2 m
5 m
4 m
(3+5)×4÷2 + (2+6)×2÷2
= 8×4÷2 + 8×2÷2
= 24(m2)
6×5 —2×3
= 30—6
= 24(m2)
方法三:分割成两个梯形
方法四:补上一个小长方形,使它成
为一个大长方形
3m
2m
2m
3m
答:至少要24平方米的地板。
答:至少要24平方米的地板。
找出对应条件计算
典题精讲
计算组合图形的面积主要可以采用“分割” 与“添补”的方法进行计算。
通过刚才的学习,你认为应怎样计算组合
图形的面积?
典题精讲
S长方形:10×8=80(cm2)
S梯形:(6+10)×2÷2=16(cm2)
S组合图形:80+16=96(cm2)
错误解答
易错提醒
S长方形:10×8=80(cm2)
S梯形:(6+10)×2÷2=16(cm2)
S组合图形:80+16=96(cm2)
错误解答
易错提醒
错解分析:组合图形的面积应该是长方形的面积减梯形的面积。
S长方形:10×8=80(cm2)
S梯形:(6+10)×2÷2=16(cm2)
S组合图形:80-16=64(cm2)
S长方形:10×8=80(cm2)
S梯形:(6+10)×2÷2=16(cm2)
S组合图形:80+16=96(cm2)
错误解答
正确解答
易错提醒
45°
阴影三角形的底和高都是2cm
三角形面积:2×2÷2=2(cm2)
S=ah÷2
学以致用
可以看成由
三角形和正
方形组成。
正方形面积:5×5=25(cm2)
三角形面积:8×5÷2=20(m2)
阴影面积:25+20=45(m2)
S=a
S=ah÷2
学以致用
求下图阴影部分的面积
4
三角形面积:4×4÷2=8(cm2)
学以致用
已知下图中平行四边形的面积是240平方厘米,求阴影部分的面积。
平行四边形的底即梯形的下底:
梯形面积:(10+16)×15÷2
=15×26÷2=195(cm2)
S=(a+b)×h÷2
学以致用
240÷15=16(cm)
可以看成由三角形+小正方形-下长三角形。
正方形面积:
5×5=25(cm )
三角形的面积:
8×8÷2=32(cm )
25+32=57(cm )
长三角形的面积:
13×5÷2=32.5(cm )
阴影面积:
57-32.5=24.5(cm )
学以致用
课堂小结
2.添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。
怎样求组合图形的面积?
1.分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。
