数学五年级上苏教版2.1 平行四边形的面积课件(共23张PPT)
文档属性
| 名称 | 数学五年级上苏教版2.1 平行四边形的面积课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-16 07:08:56 | ||
图片预览





文档简介
(共23张PPT)
第2单元 多边形的面积
1 平行四边形的面积
学习目标
2.通过操作和对图形的观察、比较,发展空间观念,初步知道转化的思考方法在研究平行四边形面积时的运用。
1.在理解的基础上,掌握平行四边形面积计算公式,能正确地计算平行四边形的面积。
3.培养分析、综合、抽象、概括和解决实际问题的能力。培养学习数学的兴趣、探究意识与合作的意识。
复习导入
同学们你们都学过哪些平面图形?
平行四边形特点:
①对边平行且相等
②对角相等
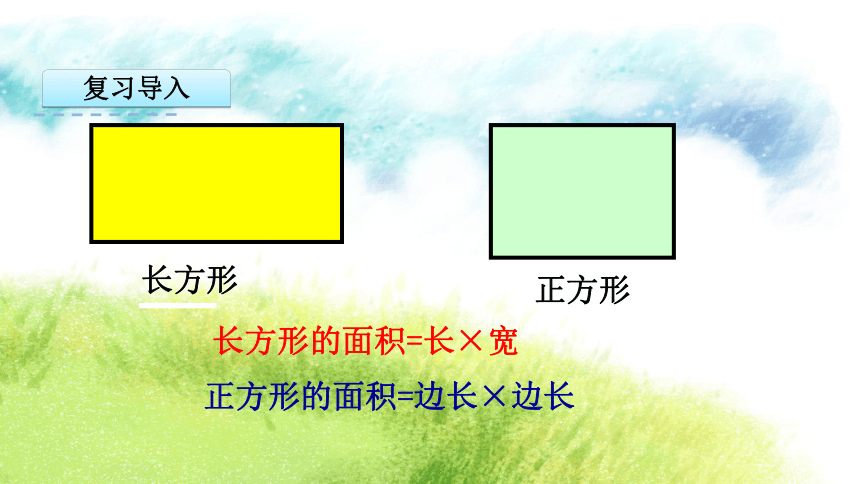
复习导入
长方形
正方形
长方形的面积=长×宽
正方形的面积=边长×边长
情景导入1
下面两个图形面积相等吗?
①
②
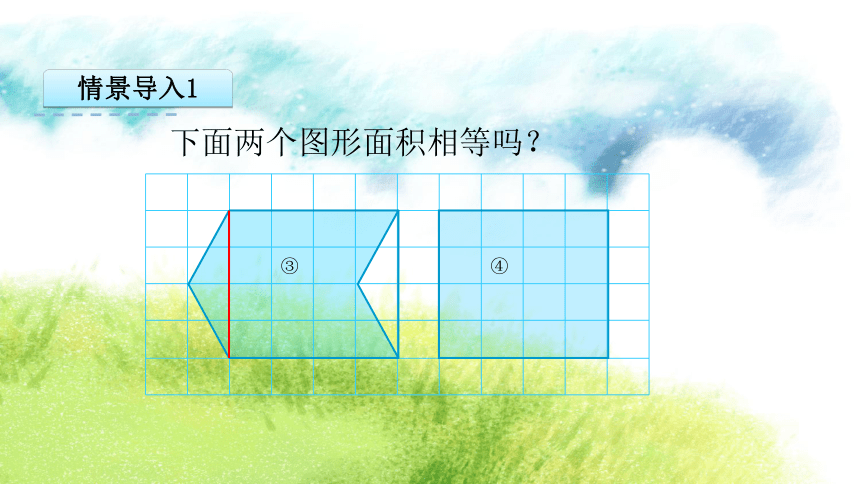
情景导入1
下面两个图形面积相等吗?
③
④
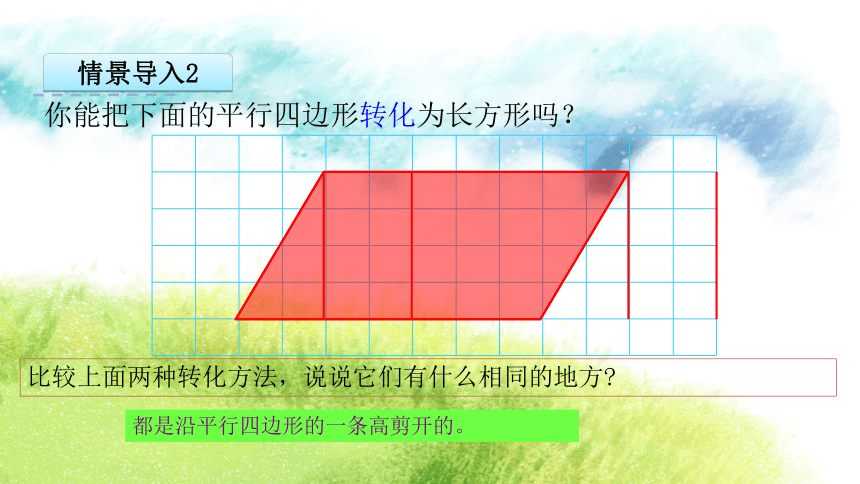
情景导入2
你能把下面的平行四边形转化为长方形吗?
比较上面两种转化方法,说说它们有什么相同的地方
都是沿平行四边形的一条高剪开的。
探究新知
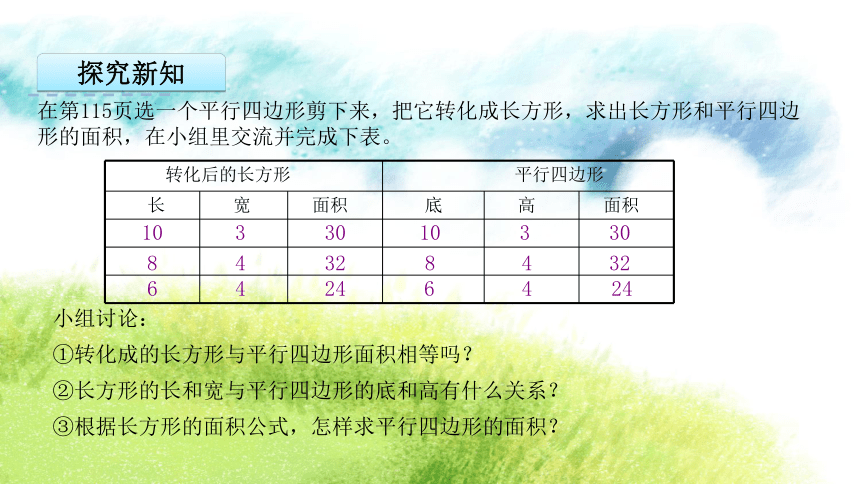
小组讨论:
①转化成的长方形与平行四边形面积相等吗?
②长方形的长和宽与平行四边形的底和高有什么关系?
③根据长方形的面积公式,怎样求平行四边形的面积?
在第115页选一个平行四边形剪下来,把它转化成长方形,求出长方形和平行四边形的面积,在小组里交流并完成下表。
转化后的长方形 平行四边形 长 宽 面积 底 高 面积
10
3
30
10
3
30
8
4
32
8
4
32
6
4
24
6
4
24
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
探究新知
探究新知
长方形的面积 = 长 × 宽
平行四边形的面积 =
高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
底
×
S = a × h
S =ah
平行四边形的面积 =
高
底
×
a
h
a
探究新知
典题精讲
12厘米
8厘米
26米
50米
12×8=96(平方厘米)
50×26=1300(平方米)
14分米
24 分米
1.算出下面每个平行四边形的面积。
24×14=336(平方分米)
平行四边形的面积 =底×高
2. 任何一个平行四边形都可以转化成一个( ),它的面积与原来的平行四 边形( )。这个长方形的长与平行四边形的( )相等,这个长方形的宽与平行四边形的( )相等。因为长方形的面积=( ),所以,平行四边形的面积=( )。
长方形
相等
底
高
长×宽
底×高
典题精讲
5cm
2cm
3.这三个平行四边形的面积相等吗?为什么?
等底等高的平行四边形,面积相等。
典题精讲
易错提醒
求下面平行四边形的面积。
30分米
20分米
25分米
25×20=500(平方分米)
30×25=750(平方分米)
错误解答
错误解答
易错提醒
30分米
20分米
25分米
25×20=500(平方分米)
30×25=750(平方分米)
错解分析:
30和25是平行四边形相邻的两条边。
25和20 不是对应的底和高。
易错提醒
求下面平行四边形的面积。
30分米
20分米
25分米
25×20=500(平方分米)
30×25=750(平方分米)
错误解答
错误解答
30×20=600(平方分米)
正确解答
观察面积和周长,你发现了什么?
1.把长方形框拉成平行四边形。
学以致用
把长方形拉成平行四边形,周长不变,面积变小。
长方形的长等于平行四边形的底;长方形的宽比平行四边形的高长。
辅助线把平行四边形平均分成2分,每份里涂色部分是小平行四边形的一半。
2 . 下图中大平行四边形的面积是 48 平方厘米。A 、B 是上下两边的中点。你能求出图中小平行四边形(涂色部分)的面积吗?
A
B
48÷2=24(平方厘米)
学以致用
3.已知一个平行四边形的底是2米,高是5分米,它的面积是( )。
A、10平方米 B、100平方分米 C、100分米
4.已知一个平行四边形的面积是30平方米,底是6米,高是( )。
A、180平方米 B、5平方米 C、5米
B
C
学以致用
学以致用
5.A、B、C中哪一个的面积是3×2=6平方厘米? ( )
2厘米
3厘米
A
3厘米
2厘米
B
2厘米
3厘米
C
C
学以致用
2 . 一个平行四边形广告牌,底6米,高2米。按每平方米50元计算,制作这个广告牌需要多少元?
提示:先求平行四边形的面积,再求广告牌的价钱。
6×2=12(平方米)
50×12=600(元)
课堂小结
2. 沿着平行四边形的任意一条高剪开,再平移;可以拼成一个长方形。这个长方形的长与平行四边形的底相等,这个长方形的宽与平行四边形的高相等。因为长方形的面积=长×宽,所以平行四边形的面积=底×高。
平行四边形的面积怎样计算?
怎样推导出平行四边形的面积公式的?
1.平行四边形的面积=底×高。
第2单元 多边形的面积
1 平行四边形的面积
学习目标
2.通过操作和对图形的观察、比较,发展空间观念,初步知道转化的思考方法在研究平行四边形面积时的运用。
1.在理解的基础上,掌握平行四边形面积计算公式,能正确地计算平行四边形的面积。
3.培养分析、综合、抽象、概括和解决实际问题的能力。培养学习数学的兴趣、探究意识与合作的意识。
复习导入
同学们你们都学过哪些平面图形?
平行四边形特点:
①对边平行且相等
②对角相等
复习导入
长方形
正方形
长方形的面积=长×宽
正方形的面积=边长×边长
情景导入1
下面两个图形面积相等吗?
①
②
情景导入1
下面两个图形面积相等吗?
③
④
情景导入2
你能把下面的平行四边形转化为长方形吗?
比较上面两种转化方法,说说它们有什么相同的地方
都是沿平行四边形的一条高剪开的。
探究新知
小组讨论:
①转化成的长方形与平行四边形面积相等吗?
②长方形的长和宽与平行四边形的底和高有什么关系?
③根据长方形的面积公式,怎样求平行四边形的面积?
在第115页选一个平行四边形剪下来,把它转化成长方形,求出长方形和平行四边形的面积,在小组里交流并完成下表。
转化后的长方形 平行四边形 长 宽 面积 底 高 面积
10
3
30
10
3
30
8
4
32
8
4
32
6
4
24
6
4
24
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
探究新知
探究新知
长方形的面积 = 长 × 宽
平行四边形的面积 =
高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
底
×
S = a × h
S =ah
平行四边形的面积 =
高
底
×
a
h
a
探究新知
典题精讲
12厘米
8厘米
26米
50米
12×8=96(平方厘米)
50×26=1300(平方米)
14分米
24 分米
1.算出下面每个平行四边形的面积。
24×14=336(平方分米)
平行四边形的面积 =底×高
2. 任何一个平行四边形都可以转化成一个( ),它的面积与原来的平行四 边形( )。这个长方形的长与平行四边形的( )相等,这个长方形的宽与平行四边形的( )相等。因为长方形的面积=( ),所以,平行四边形的面积=( )。
长方形
相等
底
高
长×宽
底×高
典题精讲
5cm
2cm
3.这三个平行四边形的面积相等吗?为什么?
等底等高的平行四边形,面积相等。
典题精讲
易错提醒
求下面平行四边形的面积。
30分米
20分米
25分米
25×20=500(平方分米)
30×25=750(平方分米)
错误解答
错误解答
易错提醒
30分米
20分米
25分米
25×20=500(平方分米)
30×25=750(平方分米)
错解分析:
30和25是平行四边形相邻的两条边。
25和20 不是对应的底和高。
易错提醒
求下面平行四边形的面积。
30分米
20分米
25分米
25×20=500(平方分米)
30×25=750(平方分米)
错误解答
错误解答
30×20=600(平方分米)
正确解答
观察面积和周长,你发现了什么?
1.把长方形框拉成平行四边形。
学以致用
把长方形拉成平行四边形,周长不变,面积变小。
长方形的长等于平行四边形的底;长方形的宽比平行四边形的高长。
辅助线把平行四边形平均分成2分,每份里涂色部分是小平行四边形的一半。
2 . 下图中大平行四边形的面积是 48 平方厘米。A 、B 是上下两边的中点。你能求出图中小平行四边形(涂色部分)的面积吗?
A
B
48÷2=24(平方厘米)
学以致用
3.已知一个平行四边形的底是2米,高是5分米,它的面积是( )。
A、10平方米 B、100平方分米 C、100分米
4.已知一个平行四边形的面积是30平方米,底是6米,高是( )。
A、180平方米 B、5平方米 C、5米
B
C
学以致用
学以致用
5.A、B、C中哪一个的面积是3×2=6平方厘米? ( )
2厘米
3厘米
A
3厘米
2厘米
B
2厘米
3厘米
C
C
学以致用
2 . 一个平行四边形广告牌,底6米,高2米。按每平方米50元计算,制作这个广告牌需要多少元?
提示:先求平行四边形的面积,再求广告牌的价钱。
6×2=12(平方米)
50×12=600(元)
课堂小结
2. 沿着平行四边形的任意一条高剪开,再平移;可以拼成一个长方形。这个长方形的长与平行四边形的底相等,这个长方形的宽与平行四边形的高相等。因为长方形的面积=长×宽,所以平行四边形的面积=底×高。
平行四边形的面积怎样计算?
怎样推导出平行四边形的面积公式的?
1.平行四边形的面积=底×高。
