人教版数学必修1:1.2.1函数的概念(1)
文档属性
| 名称 | 人教版数学必修1:1.2.1函数的概念(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-16 10:50:40 | ||
图片预览







文档简介
课件32张PPT。1.2.1
函数的概念(1) 清晨,太阳从东方冉冉升起;
随着二氧化碳的大量排放,地球正在逐渐变暖;
中国的国内生产总值在逐年增长. 想一想:
上述三个现象中,从数学的角度看,你认为有哪些共同特点?
函数 清晨,太阳从东方冉冉升起;
随着二氧化碳的大量排放,地球正在逐渐变暖;
中国的国内生产总值在逐年增长. 在这些变化着的现象中,都存在着两个变量,当一个变量变化时,另一个变量随之发生变化.
在初中数学中有没有学过类似的知识? 设在一个变化过程中有两个变量x与y, 如果对于x的每一个值, y都有惟一的值与它对应, 那么就说 y是 x的函数, x叫做自变量.
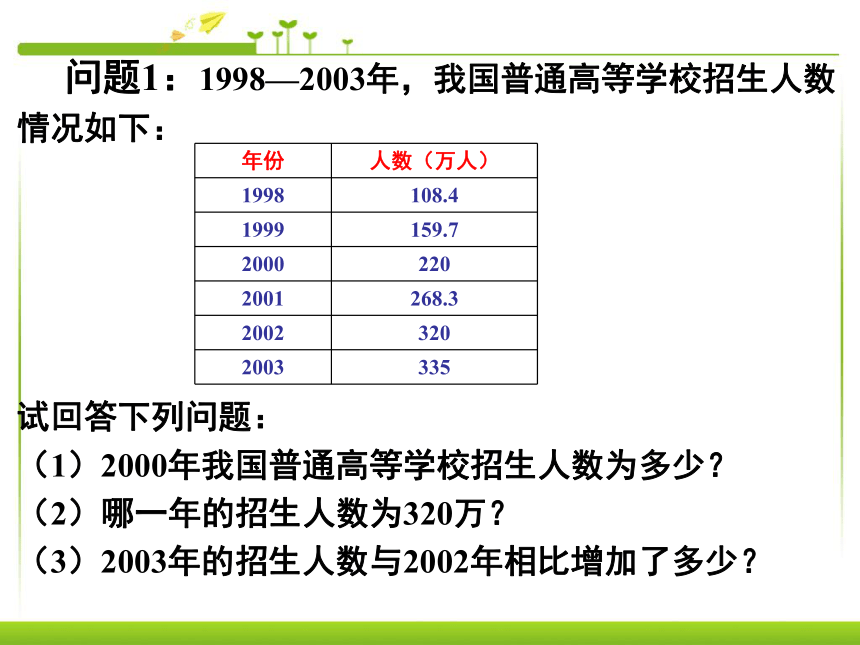
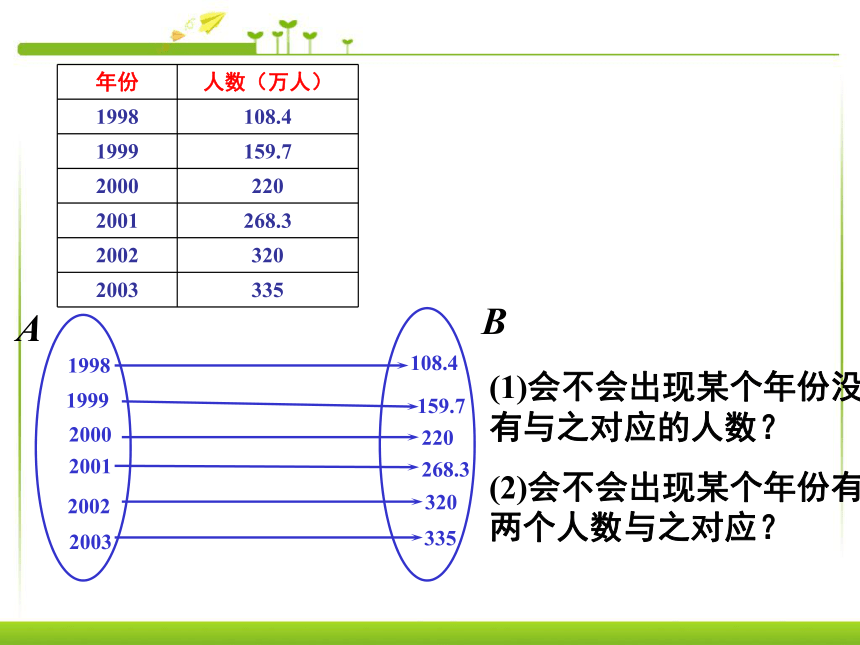
初中函数的概念请同学们举一些函数的例子. 问题1:1998—2003年,我国普通高等学校招生人数
情况如下:
试回答下列问题:
(1)2000年我国普通高等学校招生人数为多少?
(2)哪一年的招生人数为320万?
(3)2003年的招生人数与2002年相比增加了多少? 问题2:一物体在490米高的位置从静止开始下落,
下落的距离y(m)与下落时间x(s)之间近似地满足关
系式y=4.9x2.
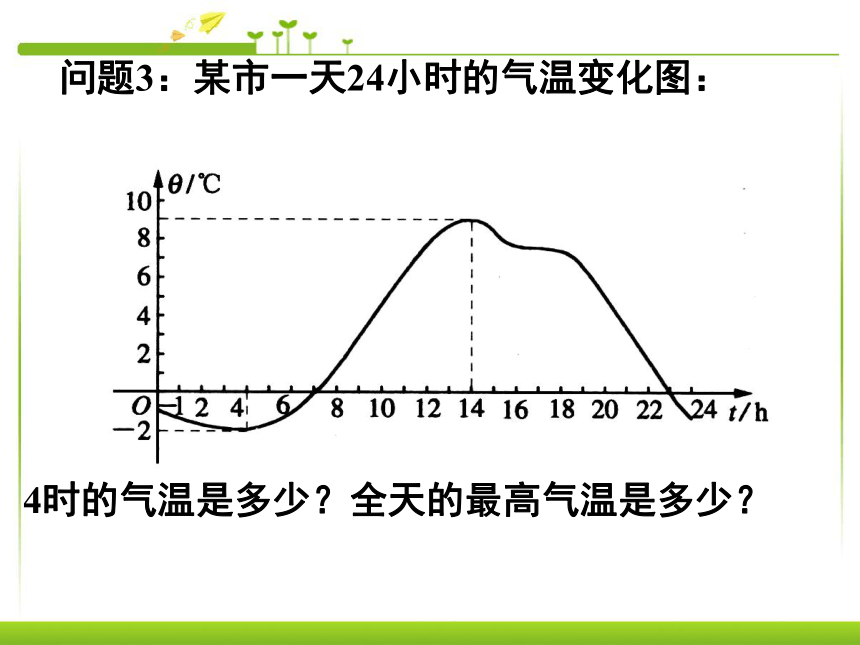
若一物体下落2s,你能求出下落的距离吗?问题3:某市一天24小时的气温变化图:4时的气温是多少?全天的最高气温是多少?
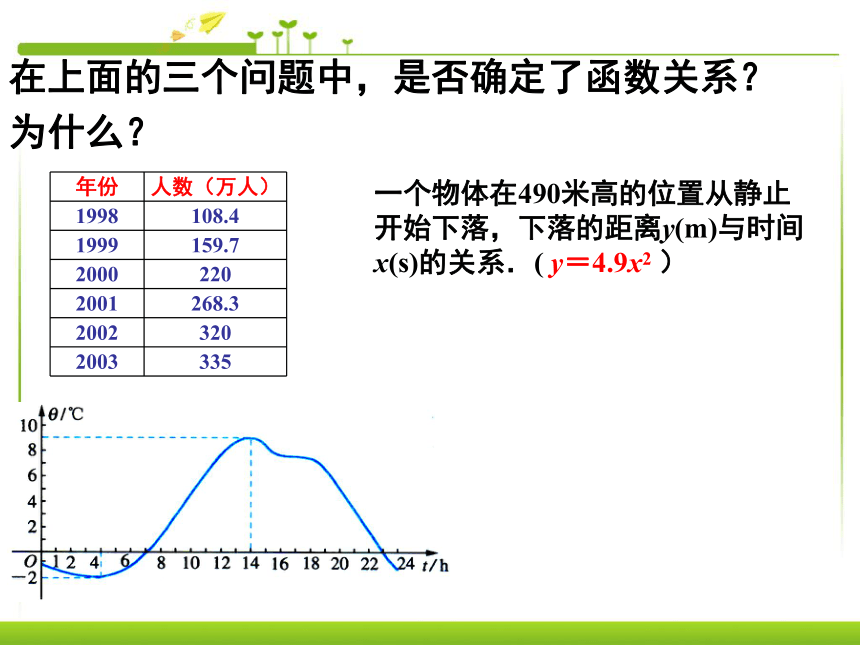
一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )在上面的三个问题中,是否确定了函数关系?
为什么? 在上述的每一个问题中都含有两个变
量,当一个变量的取值确定后,另一个变
量的值随之惟一确定,每一个问题确定了
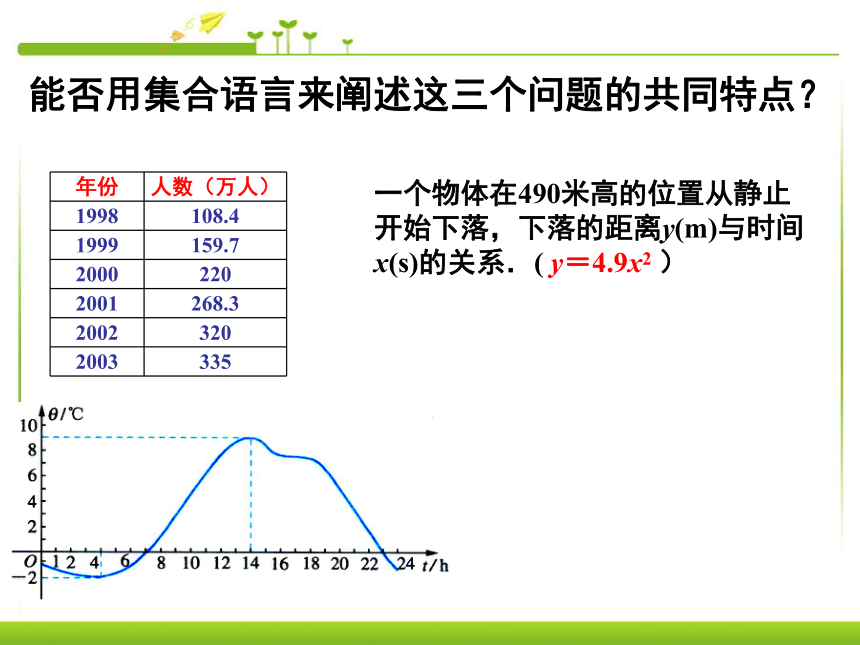
一个函数关系. 一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )能否用集合语言来阐述这三个问题的共同特点?199819992000200120022003108.4159.7220268.3320335(1)会不会出现某个年份没 有与之对应的人数?
(2)会不会出现某个年份有两个人数与之对应?AB{1998,1999 ,2000,2001,2002,2003}{108.4,159.7,220,268.3,320,335}非空数集A非空数集B一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )对于集合A中的每一个元素 x,在集合B中都有惟一的元素 y 和它对应,
记作: f:A→B{x|0≤x≤10}{y|0≤y≤490}{x|0≤x≤24}{t|-2≤t≤9} 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数
记作: y=f (x),x?A1. 定义 其中,x叫做自变量,x的取值范围A叫做函数的定义域;
与x值相对应的y的值叫做函数值,
函数值的集合{ f (x) | x ? A}叫做函数
的值域.设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,
记作: y=f (x),x?A
思考:一次函数,反比例函数、二次函数的定义域、值域各是什么?2.已学函数的定义域和值域定义域R,值域R.定义域{x|x≠0},值域{y|y≠0}.⑴ 一次函数f(x)=ax+b(a≠0)⑵2.已学函数的定义域和值域⑶二次函数f(x)=ax2+bx+c (a≠0)定义域:R, 例1.结合函数的定义,判断下列对应是不是从数
集A到数集B的函数.(1)(4)(3)(2)ABf1224368集合B和值域是什么关系?该函数的值域是什么? 定义域A;
值域{f(x)|x∈R};;
对应法则f.(2) f 表示对应法则,不同函数中f 的具
体含义不一样.函数符号y=f (x) 表示y是x的函数,
f (x)不是表示 f 与x的乘积;3. 函数的三要素:4.区间的概念:这里的实数a与b都叫做相应区间的端点.注意:用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点. 实数集R可以用区间表示为(-∞,+∞),“∞”读作“无穷大”,“-∞”读作“负无穷大”, “+∞”读作“正无穷大”.
满足x≥a,x>a,x≤b,x[a, +∞)、(a, +∞)、(-∞,b]、(-∞,b).例2.试用区间表示下列实集:
{x|5 ≤ x<6} (2) {x|x ≥9}
(3) {x|x ≤ -1} ∩{x| -5 ≤ x<2}
(4) {x|x < 9}∪{x| -9 < x<20}例3.判断下列对应是不是数集A到数集B的一个函数 (2) A=B=[0,+∞),x→y,y是x的算术平方根.(1) A={ 1,2,3,4,5},B={2,4,6,8},y=2x.(3) A=[0,+∞) ,B=R,x→y,y是x的平方根.(4) A=[0,4],B=[0,2],x→y, y= x.1 .下列说法中,不正确的是( )
A、函数值域中的第一个数都有定义域中的一个数与之对应
B、函数的定义域和值域一定是无限集合
C、定义域和对应关系确定后,函数值域也就确定
D、若函数的定义域只有一个元素,则值域也只有一个元素B练习:2.给出四个命题: ①函数就是定义域到值域的对应关系 ②若函数的定义域只含有一个元素,则值域也只有一个元素 ③因f(x)=5(x∈R),这个函数值不随x的变化范围而变化,所以f(0)=5也成立 ④定义域和对应关系确定后,函数值也就确定了 .
正确有( )
A、1个 B、2个 C、3个 D、4个D课后思考通过本节课的学习,你对函数有了什么样新的认识?课堂小结1.函数的概念;构成函数的三要素;
2.区间的表示方法.
随着二氧化碳的大量排放,地球正在逐渐变暖;
中国的国内生产总值在逐年增长. 想一想:
上述三个现象中,从数学的角度看,你认为有哪些共同特点?
函数 清晨,太阳从东方冉冉升起;
随着二氧化碳的大量排放,地球正在逐渐变暖;
中国的国内生产总值在逐年增长. 在这些变化着的现象中,都存在着两个变量,当一个变量变化时,另一个变量随之发生变化.
在初中数学中有没有学过类似的知识? 设在一个变化过程中有两个变量x与y, 如果对于x的每一个值, y都有惟一的值与它对应, 那么就说 y是 x的函数, x叫做自变量.
初中函数的概念请同学们举一些函数的例子. 问题1:1998—2003年,我国普通高等学校招生人数
情况如下:
试回答下列问题:
(1)2000年我国普通高等学校招生人数为多少?
(2)哪一年的招生人数为320万?
(3)2003年的招生人数与2002年相比增加了多少? 问题2:一物体在490米高的位置从静止开始下落,
下落的距离y(m)与下落时间x(s)之间近似地满足关
系式y=4.9x2.
若一物体下落2s,你能求出下落的距离吗?问题3:某市一天24小时的气温变化图:4时的气温是多少?全天的最高气温是多少?
一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )在上面的三个问题中,是否确定了函数关系?
为什么? 在上述的每一个问题中都含有两个变
量,当一个变量的取值确定后,另一个变
量的值随之惟一确定,每一个问题确定了
一个函数关系. 一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )能否用集合语言来阐述这三个问题的共同特点?199819992000200120022003108.4159.7220268.3320335(1)会不会出现某个年份没 有与之对应的人数?
(2)会不会出现某个年份有两个人数与之对应?AB{1998,1999 ,2000,2001,2002,2003}{108.4,159.7,220,268.3,320,335}非空数集A非空数集B一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )对于集合A中的每一个元素 x,在集合B中都有惟一的元素 y 和它对应,
记作: f:A→B{x|0≤x≤10}{y|0≤y≤490}{x|0≤x≤24}{t|-2≤t≤9} 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数
记作: y=f (x),x?A1. 定义 其中,x叫做自变量,x的取值范围A叫做函数的定义域;
与x值相对应的y的值叫做函数值,
函数值的集合{ f (x) | x ? A}叫做函数
的值域.设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,
记作: y=f (x),x?A
思考:一次函数,反比例函数、二次函数的定义域、值域各是什么?2.已学函数的定义域和值域定义域R,值域R.定义域{x|x≠0},值域{y|y≠0}.⑴ 一次函数f(x)=ax+b(a≠0)⑵2.已学函数的定义域和值域⑶二次函数f(x)=ax2+bx+c (a≠0)定义域:R, 例1.结合函数的定义,判断下列对应是不是从数
集A到数集B的函数.(1)(4)(3)(2)ABf1224368集合B和值域是什么关系?该函数的值域是什么? 定义域A;
值域{f(x)|x∈R};;
对应法则f.(2) f 表示对应法则,不同函数中f 的具
体含义不一样.函数符号y=f (x) 表示y是x的函数,
f (x)不是表示 f 与x的乘积;3. 函数的三要素:4.区间的概念:这里的实数a与b都叫做相应区间的端点.注意:用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点. 实数集R可以用区间表示为(-∞,+∞),“∞”读作“无穷大”,“-∞”读作“负无穷大”, “+∞”读作“正无穷大”.
满足x≥a,x>a,x≤b,x
{x|5 ≤ x<6} (2) {x|x ≥9}
(3) {x|x ≤ -1} ∩{x| -5 ≤ x<2}
(4) {x|x < 9}∪{x| -9 < x<20}例3.判断下列对应是不是数集A到数集B的一个函数 (2) A=B=[0,+∞),x→y,y是x的算术平方根.(1) A={ 1,2,3,4,5},B={2,4,6,8},y=2x.(3) A=[0,+∞) ,B=R,x→y,y是x的平方根.(4) A=[0,4],B=[0,2],x→y, y= x.1 .下列说法中,不正确的是( )
A、函数值域中的第一个数都有定义域中的一个数与之对应
B、函数的定义域和值域一定是无限集合
C、定义域和对应关系确定后,函数值域也就确定
D、若函数的定义域只有一个元素,则值域也只有一个元素B练习:2.给出四个命题: ①函数就是定义域到值域的对应关系 ②若函数的定义域只含有一个元素,则值域也只有一个元素 ③因f(x)=5(x∈R),这个函数值不随x的变化范围而变化,所以f(0)=5也成立 ④定义域和对应关系确定后,函数值也就确定了 .
正确有( )
A、1个 B、2个 C、3个 D、4个D课后思考通过本节课的学习,你对函数有了什么样新的认识?课堂小结1.函数的概念;构成函数的三要素;
2.区间的表示方法.
