人教版数学必修1:1.3.1单调性与最大(小)值
文档属性
| 名称 | 人教版数学必修1:1.3.1单调性与最大(小)值 |

|
|
| 格式 | zip | ||
| 文件大小 | 433.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-16 00:00:00 | ||
图片预览







文档简介
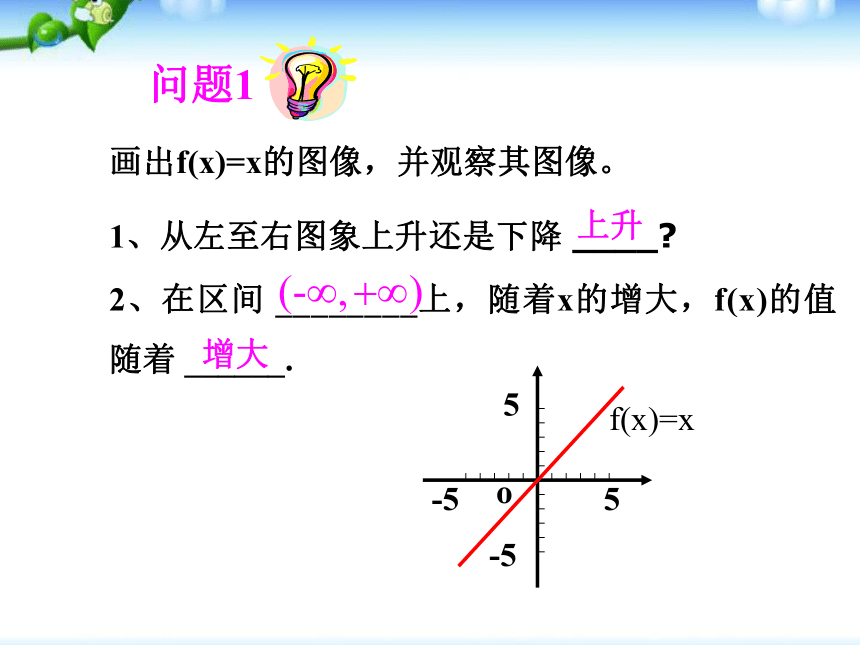
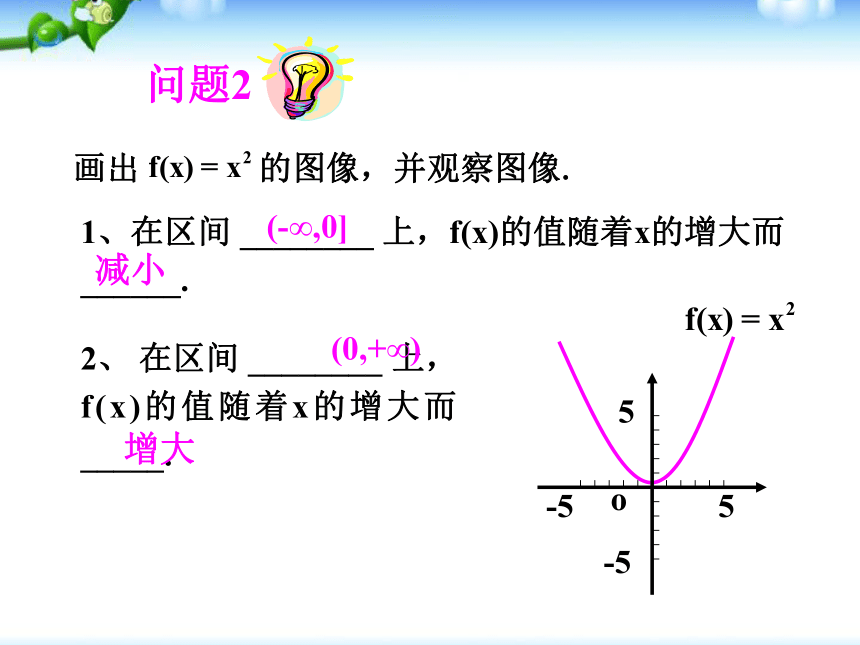
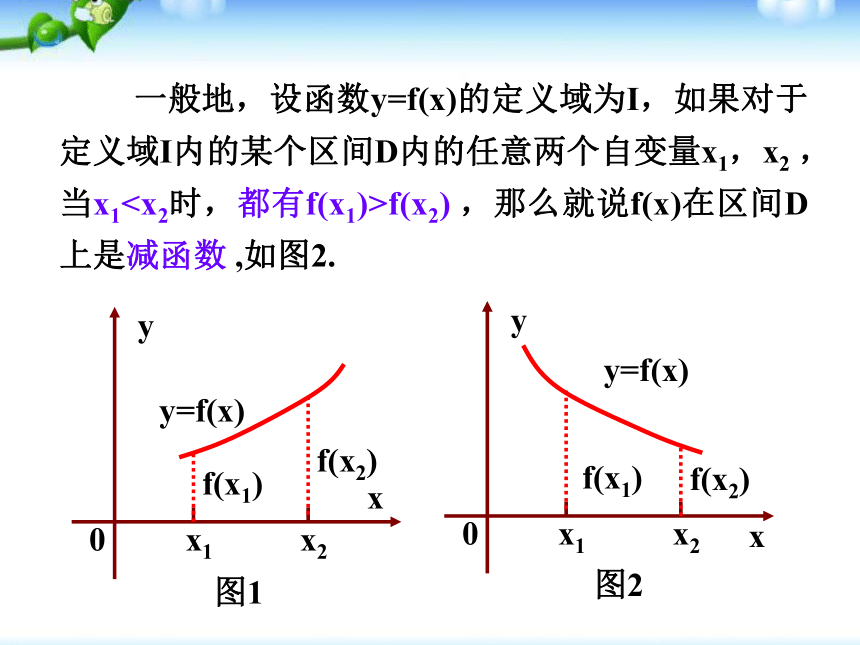
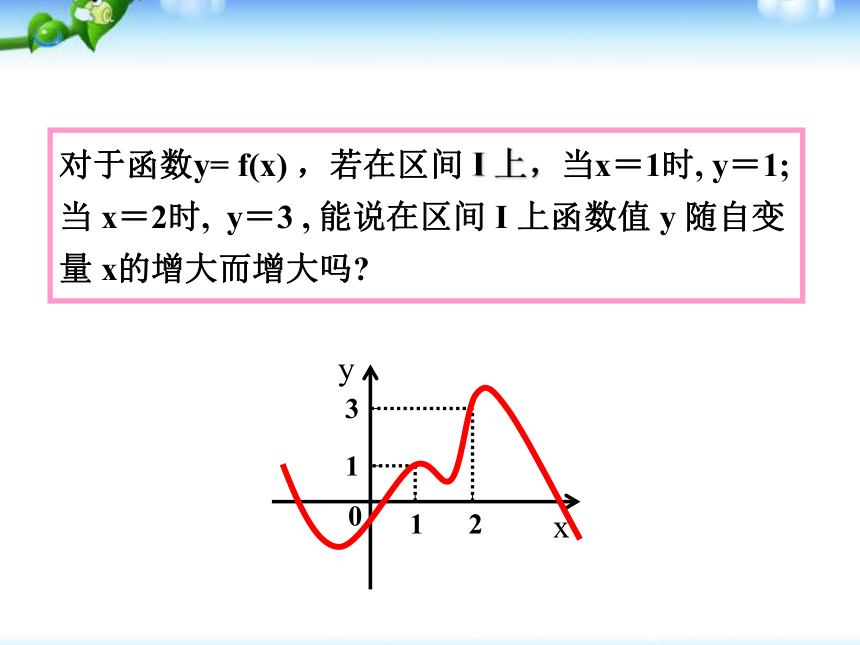
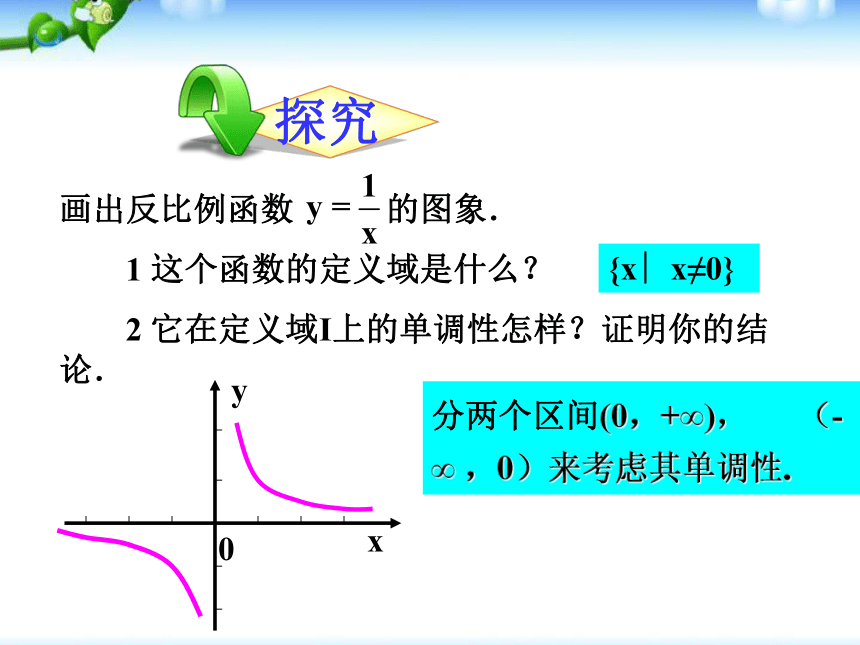
课件32张PPT。1.3.1 单调性与最大(小)值画出f(x)=x的图像,并观察其图像。2、在区间 ________上,随着x的增大,f(x)的值随着 ______. 1、从左至右图象上升还是下降 ____?上升增大1、在区间 ________ 上,f(x)的值随着x的增大而 ______.2、 在区间 ________ 上,f(x)的值随着x的增大而 _____. (-∞,0](0,+∞)减小增大函数单调性的概念: 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1f(x2) ,那么就说f(x)在区间D上是减函数 ,如图2. 1、函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质. 2 、必须是对于区间D内的任意两个自变量x1,x2;当x1f(x2) 分别是增函数和减函数.对于函数y= f(x) ,若在区间 I 上,当x=1时, y=1; 当 x=2时, y=3 , 能说在区间 I 上函数值 y 随自变量 x的增大而增大吗? 如果函数y=f(x)在某个区间上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.函数的单调性定义用定义证明函数单调性的步骤是:(1)取值(2)作差变形(3)定号(4)判断根据单调性的定义得结论思考{x∣x≠0}分两个区间(0,+∞), (- ∞ ,0)来考虑其单调性.(2)在区间(- ∞ ,0)上,同理可得到函数f(x)=1/x 在(- ∞ ,0)上是减函数。综上所述,函数f(x)=1/x 在定义域上是减函数.下列两个函数的图象: f(x)< M?(0)=12、存在0,使得?(0)=1.1是此函数的最大值知识要点M是函数y= f (x)的最大值(maximum value):是函数f(x)在定义域中既有最大值又有最小值.探究:函数单调性与函数的最值的关系(1)若函数y=f (x)在区间[m,n] (m(2)利用图象求函数的最值;
(3)利用函数单调性求函数的最值 .1.填表函数单调区间k >0k <0k >0k <0增函数减函数减函数增函数单调性函数单调区间单调性增函数增函数减函数减函数最大0.50.2-2
(3)利用函数单调性求函数的最值 .1.填表函数单调区间k >0k <0k >0k <0增函数减函数减函数增函数单调性函数单调区间单调性增函数增函数减函数减函数最大0.50.2-2
