数学五年级上苏教版7.2 解决问题的策略(2)课件(共31张PPT)
文档属性
| 名称 | 数学五年级上苏教版7.2 解决问题的策略(2)课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-16 16:15:35 | ||
图片预览









文档简介
课件31张PPT。第7单元 解决问题的策略2 解决问题
的策略(2)学习目标2.进一步培养思考数学问题的条理性、有序性,进一步体会解决数学问题方法的多样性和灵活性,发展思维能力。
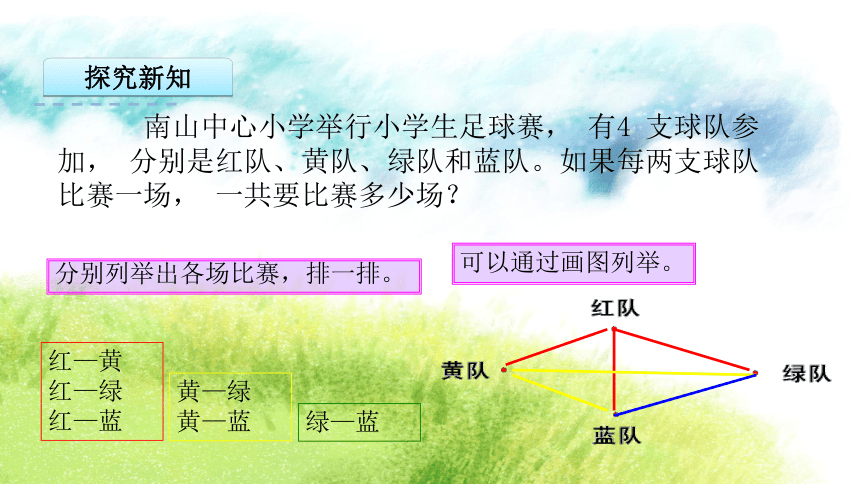
1.在解决问题的过程中体验并掌握列举的策略,会用这些策略解决一些稍复杂的实际问题。两个人玩,会有多少种不同的结果?复习导入 南山中心小学举行小学生足球赛, 有4 支球队参加, 分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场, 一共要比赛多少场?“每两支球队比赛一场”是什么意思?情景导入 南山中心小学举行小学生足球赛, 有4 支球队参加, 分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场, 一共要比赛多少场?两支球队之间只进行一场比赛。每支球队要分别与其他3支球队赛一场。探究新知 南山中心小学举行小学生足球赛, 有4 支球队参加, 分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场, 一共要比赛多少场?你打算怎样解决这个问题?先试一试,再与同学交流。探究新知 南山中心小学举行小学生足球赛, 有4 支球队参加, 分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场, 一共要比赛多少场?分别列举出各场比赛,排一排。红—黄
红—绿
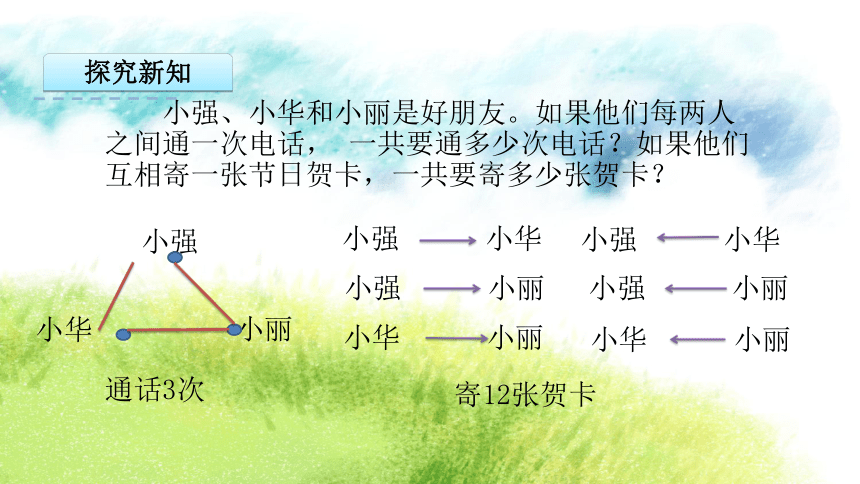
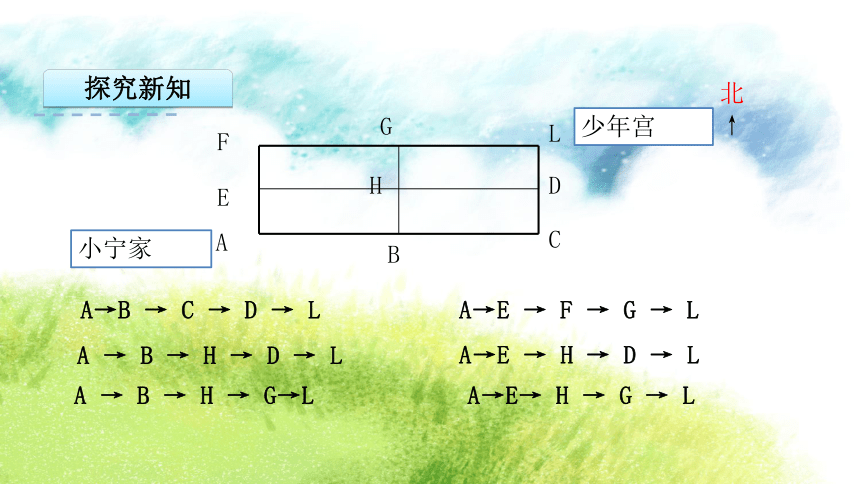
红—蓝 黄—绿黄—蓝可以通过画图列举。绿—蓝探究新知可以根据问题的特点,选择合适的列举方法。列举时,可以列表,也可以画图。列举出全部结果后,要进行检查。探究新知 小强、小华和小丽是好朋友。如果他们每两人之间通一次电话, 一共要通多少次电话?如果他们互相寄一张节日贺卡,一共要寄多少张贺卡?小强小华小丽通话3次寄12张贺卡探究新知 小宁从家到少年宫,如果只能向北走或向东走,一共有多少种不同的行走路线?探究新知ABCEDFGLHA→B → C → D → L
A → B → H → D → LA → B → H → G→LA→E → F → G → LA→E → H → D → LA→E→ H → G → L探究新知 某班有46名同学去划船,大船限坐6人,每条船租金20元,小船限坐4人,每条船租金10元,可以怎样租船?哪种方案最省钱?探究新知大船6人,20元;小船4人,10元01234567812109764310120120130130140140150150160探究新知有 A、 B、 C 三个网站, 分别是每两天、 三天、 四天更新一次。某月 1 日三个网站同时更新后, 到这个月15 日, 哪几天没有网站更新? 哪一天三个网站又同时更新? (先在下表里画一画, 再回答)
典题精讲有 A、 B、 C 三个网站, 分别是每两天、 三天、 四天更新一次。某月 1 日三个网站同时更新后, 到这个月15 日, 哪几天没有网站更新? 哪一天三个网站又同时更新? (先在下表里画一画, 再回答)
答:到这个月15日, 日没
有网站更新, 日三个网站又同时更新。
2日、6日、8日、12日、1413典题精讲两个自然数相乘,积是36的算式有多少个? 答:积是36的算式有9个。1×36=362×18=363×12=364 × 9=366 × 6=3636×1=3618×2=3612×3=369 ×4=36典题精讲数一数右图中一共有多少个正方形?有9个有4个有1个典题精讲 一张靶纸共三圈,投中内圈得10环,投中中圈得8环,投中外圈得6 环。小华投中1次,可能得多少环?投中2次呢?√√√√√√√√√√√√小华投中两次的情况:典题精讲 一张靶纸共三圈,投中内圈得10环,投中中圈得8环,投中外圈得6 环。小华投中三次,可能得到多少种不同的环数?
三次环数相同:?10+10+10=30?8+8+8=24?6+6+6=18两次环数相同:?10+10+8=28?10+10+6=26?8+8+10 =26 ? 8+8+6=22?6+6+10=22?6+6+8=20三次环数不同:?10+8+6=24答:可能得到30、24、18、28、26、22、20这七种不同的环数。典题精讲一枚二枚三枚四枚100
80100+100=20080+80=160
100+80=180100+100+80=280
100+80+80=260
100+100+80+80
=3602+3+2+1=8(种) 小芳有下面4枚邮票,用这些邮票能付多少种不同的邮资?像这种问题,先进行合理的分类,再分类
列举,能更好地做到不重复、不遗漏。学以致用只选一枚邮票选两枚邮票选三枚邮票选四枚邮票学以致用√√√√√√√√√√√√√√√√√√10018016028026036020080一共8种学以致用 王大叔要用22根1米长的木条一面靠墙,围成一个长方形花圃,怎样围面积最大?学以致用 王大叔要用22根1米长的木条一面靠墙,围成一个长方形花圃,怎样围面积最大?20181614121086421234567891020364856606056483620学以致用 两个小于1的一位小数相加,和是1.2。符合要求的算式一共有多少道?你能按顺序写出所有符合要求的算式吗?(加数相同的算式只算一种)0.6+0.6=1.20.3+0.9=1.20.4+0.8=1.20.5+0.7=1.2学以致用 一个平行四边形的面积是24平方米,它的底和高分别是多少? (底、高是整米数)一共有多少种不同的情况?(列表解决问题)答:一共有8种不同的情况。学以致用有1克、2克、4克的砝码各1个,选其中的一个或几个,能在天平上直接称出多少种不同质量的物体?学以致用 现有1克、3克、5克的砝码各一个(砝码放右盘),
在天平上最多能称出多少种不同的重量?
答;在天平上最多能称出7种不同的重量。学以致用 有红、绿、蓝、黄、白五种颜色的铅笔,每两色的铅笔为一组。最多可以配成几组不重复的?4+3+2+1=10(种)
答:最多可以配成10
组不重复的。学以致用一共能称出7种不同的质量。姐姐和弟弟一起把妈妈买来的8块巧克力吃完了。姐姐说:“两个人都吃了。”弟弟说:“我们每人吃的块数不同。”你知道他们俩一共有几种不同的吃法吗?学以致用课堂小结2.列举时要按照一定的顺序有条理地进行,做到不重复,不遗漏。1.当问题的答案有多种可能或要从多种可能中找出最合理的答案时,一般运用一一列举的策略来解决。
的策略(2)学习目标2.进一步培养思考数学问题的条理性、有序性,进一步体会解决数学问题方法的多样性和灵活性,发展思维能力。
1.在解决问题的过程中体验并掌握列举的策略,会用这些策略解决一些稍复杂的实际问题。两个人玩,会有多少种不同的结果?复习导入 南山中心小学举行小学生足球赛, 有4 支球队参加, 分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场, 一共要比赛多少场?“每两支球队比赛一场”是什么意思?情景导入 南山中心小学举行小学生足球赛, 有4 支球队参加, 分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场, 一共要比赛多少场?两支球队之间只进行一场比赛。每支球队要分别与其他3支球队赛一场。探究新知 南山中心小学举行小学生足球赛, 有4 支球队参加, 分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场, 一共要比赛多少场?你打算怎样解决这个问题?先试一试,再与同学交流。探究新知 南山中心小学举行小学生足球赛, 有4 支球队参加, 分别是红队、黄队、绿队和蓝队。如果每两支球队比赛一场, 一共要比赛多少场?分别列举出各场比赛,排一排。红—黄
红—绿
红—蓝 黄—绿黄—蓝可以通过画图列举。绿—蓝探究新知可以根据问题的特点,选择合适的列举方法。列举时,可以列表,也可以画图。列举出全部结果后,要进行检查。探究新知 小强、小华和小丽是好朋友。如果他们每两人之间通一次电话, 一共要通多少次电话?如果他们互相寄一张节日贺卡,一共要寄多少张贺卡?小强小华小丽通话3次寄12张贺卡探究新知 小宁从家到少年宫,如果只能向北走或向东走,一共有多少种不同的行走路线?探究新知ABCEDFGLHA→B → C → D → L
A → B → H → D → LA → B → H → G→LA→E → F → G → LA→E → H → D → LA→E→ H → G → L探究新知 某班有46名同学去划船,大船限坐6人,每条船租金20元,小船限坐4人,每条船租金10元,可以怎样租船?哪种方案最省钱?探究新知大船6人,20元;小船4人,10元01234567812109764310120120130130140140150150160探究新知有 A、 B、 C 三个网站, 分别是每两天、 三天、 四天更新一次。某月 1 日三个网站同时更新后, 到这个月15 日, 哪几天没有网站更新? 哪一天三个网站又同时更新? (先在下表里画一画, 再回答)
典题精讲有 A、 B、 C 三个网站, 分别是每两天、 三天、 四天更新一次。某月 1 日三个网站同时更新后, 到这个月15 日, 哪几天没有网站更新? 哪一天三个网站又同时更新? (先在下表里画一画, 再回答)
答:到这个月15日, 日没
有网站更新, 日三个网站又同时更新。
2日、6日、8日、12日、1413典题精讲两个自然数相乘,积是36的算式有多少个? 答:积是36的算式有9个。1×36=362×18=363×12=364 × 9=366 × 6=3636×1=3618×2=3612×3=369 ×4=36典题精讲数一数右图中一共有多少个正方形?有9个有4个有1个典题精讲 一张靶纸共三圈,投中内圈得10环,投中中圈得8环,投中外圈得6 环。小华投中1次,可能得多少环?投中2次呢?√√√√√√√√√√√√小华投中两次的情况:典题精讲 一张靶纸共三圈,投中内圈得10环,投中中圈得8环,投中外圈得6 环。小华投中三次,可能得到多少种不同的环数?
三次环数相同:?10+10+10=30?8+8+8=24?6+6+6=18两次环数相同:?10+10+8=28?10+10+6=26?8+8+10 =26 ? 8+8+6=22?6+6+10=22?6+6+8=20三次环数不同:?10+8+6=24答:可能得到30、24、18、28、26、22、20这七种不同的环数。典题精讲一枚二枚三枚四枚100
80100+100=20080+80=160
100+80=180100+100+80=280
100+80+80=260
100+100+80+80
=3602+3+2+1=8(种) 小芳有下面4枚邮票,用这些邮票能付多少种不同的邮资?像这种问题,先进行合理的分类,再分类
列举,能更好地做到不重复、不遗漏。学以致用只选一枚邮票选两枚邮票选三枚邮票选四枚邮票学以致用√√√√√√√√√√√√√√√√√√10018016028026036020080一共8种学以致用 王大叔要用22根1米长的木条一面靠墙,围成一个长方形花圃,怎样围面积最大?学以致用 王大叔要用22根1米长的木条一面靠墙,围成一个长方形花圃,怎样围面积最大?20181614121086421234567891020364856606056483620学以致用 两个小于1的一位小数相加,和是1.2。符合要求的算式一共有多少道?你能按顺序写出所有符合要求的算式吗?(加数相同的算式只算一种)0.6+0.6=1.20.3+0.9=1.20.4+0.8=1.20.5+0.7=1.2学以致用 一个平行四边形的面积是24平方米,它的底和高分别是多少? (底、高是整米数)一共有多少种不同的情况?(列表解决问题)答:一共有8种不同的情况。学以致用有1克、2克、4克的砝码各1个,选其中的一个或几个,能在天平上直接称出多少种不同质量的物体?学以致用 现有1克、3克、5克的砝码各一个(砝码放右盘),
在天平上最多能称出多少种不同的重量?
答;在天平上最多能称出7种不同的重量。学以致用 有红、绿、蓝、黄、白五种颜色的铅笔,每两色的铅笔为一组。最多可以配成几组不重复的?4+3+2+1=10(种)
答:最多可以配成10
组不重复的。学以致用一共能称出7种不同的质量。姐姐和弟弟一起把妈妈买来的8块巧克力吃完了。姐姐说:“两个人都吃了。”弟弟说:“我们每人吃的块数不同。”你知道他们俩一共有几种不同的吃法吗?学以致用课堂小结2.列举时要按照一定的顺序有条理地进行,做到不重复,不遗漏。1.当问题的答案有多种可能或要从多种可能中找出最合理的答案时,一般运用一一列举的策略来解决。
