1.2 图形的全等同步练习
图片预览

文档简介
1.2 图形的全等
新知识记:
1.全等图形
(1)定义:能够 的两个图形。
(2)特点: 和 都相同。
2.全等三角形
(1)定义:能够 的两个三角形。
(2)对应元素:
① 的顶点叫做对应顶点;
② 的边叫做对应边;
③ 的角叫做对应角。
(3)表示方法:
①表示:△ABC和△DEF全等,记作△ABC △DEF;
②注意:记两个三角形全等时,把表示对应顶点的字母写在 位置上。
(4)性质:
①全等三角形的对应边 ;
②全等三角形的对应角 。
知识点一 全等形、全等三角形的有关概念
【典例 1】如图,已知△ABE和△ACD全等,∠ADE = ∠AED,∠B = ∠C,指出全等三 A
角形中其他的对应边和对应角。
【规范解答】因为∠B = ∠C,∠ADE = ∠AED,所以∠B与∠C,
∠ADE与∠AED分别是△ABE和△ACD的对应角,
所以∠BAE与∠CAD是对应角;(全等三角形对应角的概念) B D E C
所以AB与AC,AE与AD,BE与CD分别是对应边。(全等三角形对应边的概念)
【变式训练】
如图,已知△ABD和△ACE全等,∠B = ∠C,BD与CE是对应边,指出全等 A
三角形中的对应边和对应角。
B D E C
知识点二 全等三角形的性质的应用
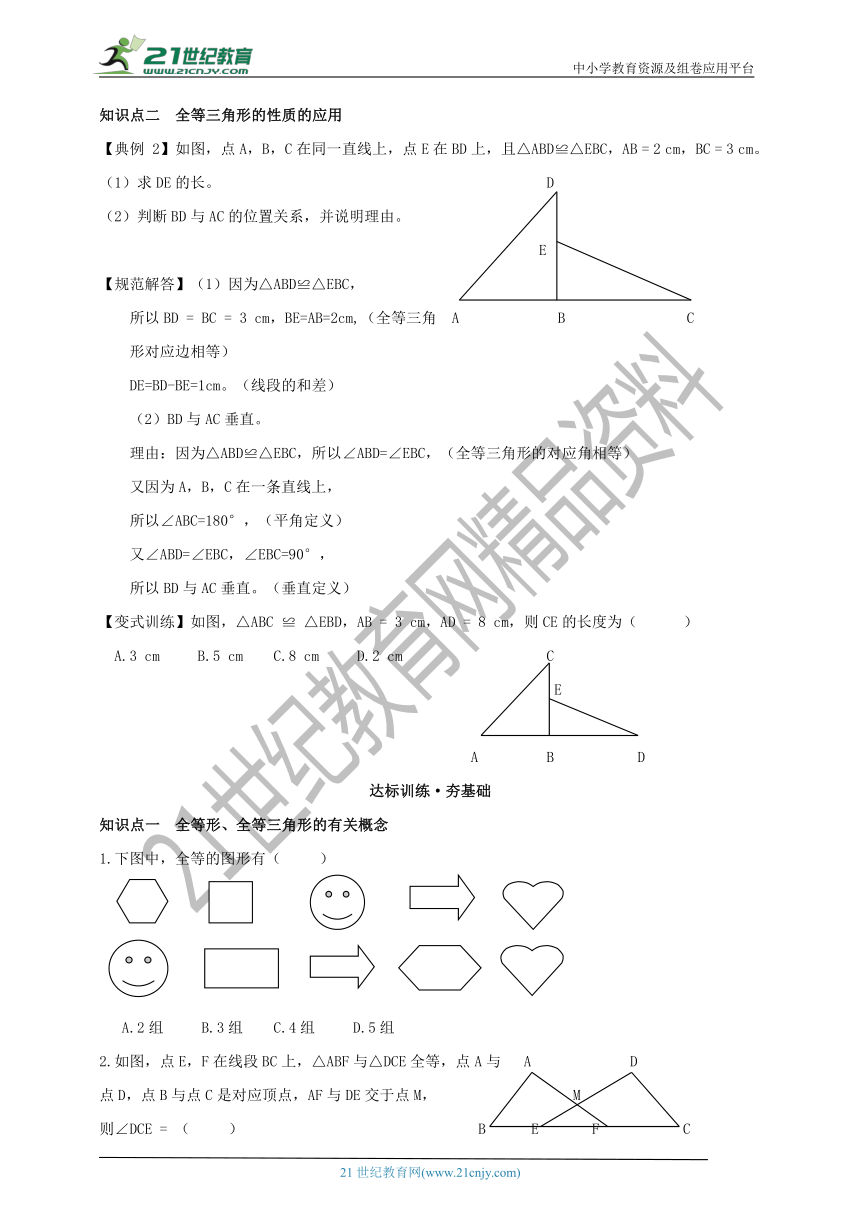
【典例 2】如图,点A,B,C在同一直线上,点E在BD上,且△ABD≌△EBC,AB = 2 cm,BC = 3 cm。
(1)求DE的长。 D
(2)判断BD与AC的位置关系,并说明理由。
E
【规范解答】(1)因为△ABD≌△EBC,
所以BD = BC = 3 cm,BE=AB=2cm,(全等三角 A B C
形对应边相等)
DE=BD-BE=1cm。(线段的和差)
(2)BD与AC垂直。
理由:因为△ABD≌△EBC,所以∠ABD=∠EBC,(全等三角形的对应角相等)
又因为A,B,C在一条直线上,
所以∠ABC=180°,(平角定义)
又∠ABD=∠EBC,∠EBC=90°,
所以BD与AC垂直。(垂直定义)
【变式训练】如图,△ABC ≌ △EBD,AB = 3 cm,AD = 8 cm,则CE的长度为( )
A.3 cm B.5 cm C.8 cm D.2 cm C
E
A B D
达标训练·夯基础
知识点一 全等形、全等三角形的有关概念
1.下图中,全等的图形有( )
A.2组 B.3组 C.4组 D.5组
2.如图,点E,F在线段BC上,△ABF与△DCE全等,点A与 A D
点D,点B与点C是对应顶点,AF与DE交于点M, M
则∠DCE = ( ) B E F C
A. ∠ B B. ∠ A C. ∠ EMF D. ∠ AFB B
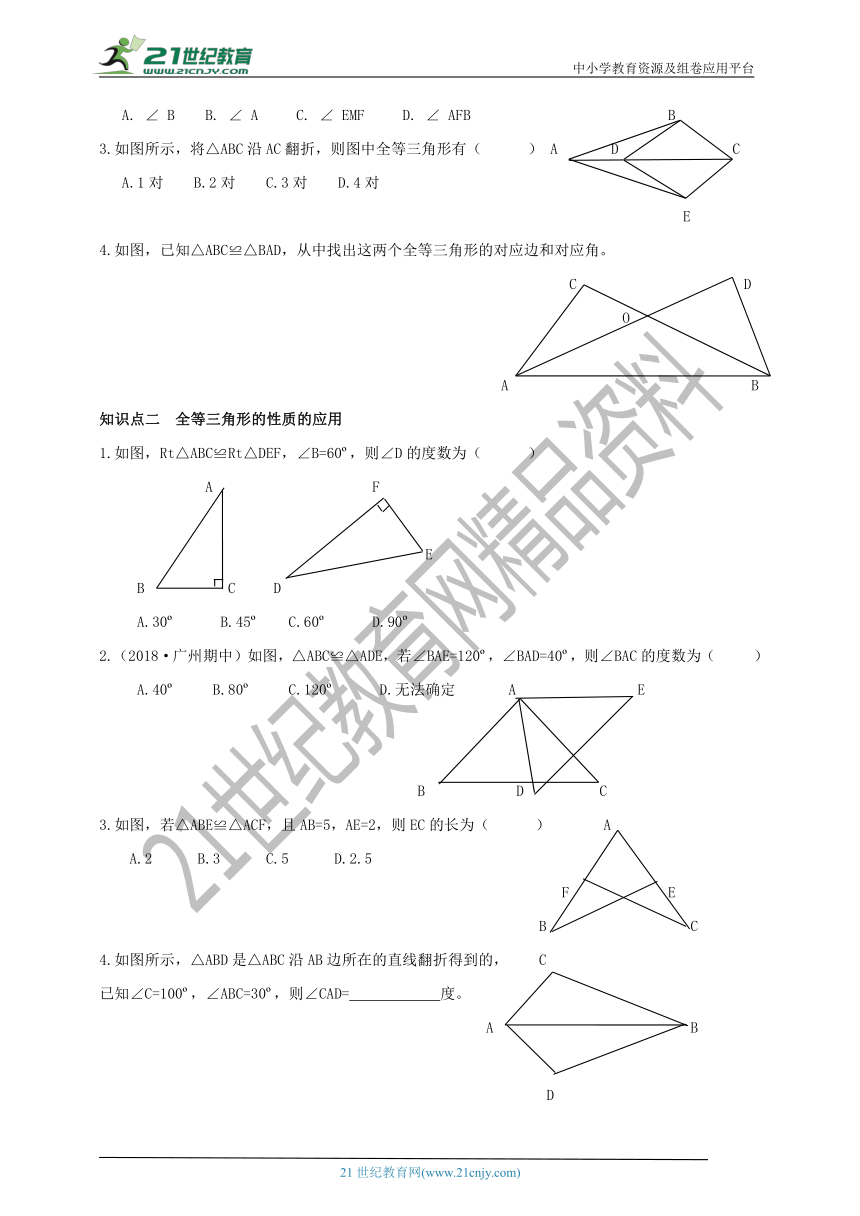
3.如图所示,将△ABC沿AC翻折,则图中全等三角形有( ) A D C
A.1对 B.2对 C.3对 D.4对
E
4.如图,已知△ABC≌△BAD,从中找出这两个全等三角形的对应边和对应角。
C D
O
A B
知识点二 全等三角形的性质的应用
1.如图,Rt△ABC≌Rt△DEF,∠B=60o,则∠D的度数为( )
A F
E
B C D
A.30o B.45o C.60o D.90o
2.(2018·广州期中)如图,△ABC≌△ADE,若∠BAE=120o,∠BAD=40o,则∠BAC的度数为( )
A.40o B.80o C.120o D.无法确定 A E
B D C
3.如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( ) A
A.2 B.3 C.5 D.2.5
F E
B C
4.如图所示,△ABD是△ABC沿AB边所在的直线翻折得到的, C
已知∠C=100o,∠ABC=30o,则∠CAD= 度。
A B
D
5.如图,已知△ABC≌△ADE。 A
(1)写出这两个三角形中相等的边和角。
(2)∠BAD与∠EAC相等吗?说明理由。 E
B D C
纠错: A D
如图,△ABC≌△DEF,则此图中相等的线段有( )
A.1对 B.2对 C.3对 D.4对
B E C F
解:选C 因为△ABC≌△DEF
所以AB=DE,AC=DF,BC=EF,那有3对线段的线段。
错因:
考题变式·提能力
(2016·成都中考)如图,△ABC≌△A’B’C’,其中∠A=36o,∠C’=24o,则∠B= 。
A A’
B B’
C C’
母题变式
如图,△ABC≌△A’B’C’,其中∠A=36o,∠B=120o,则∠C’= 。
A A’
B B’
C C’
参考答案及解析
新知识记:
(1)完全重合 (2)形状 大小
(1)完全重合 (2)①重合 ②重合 ③重合 (3)①≌ ②对应
①相等 ②相等
典例精析·拓新知
【典例 1】【变式训练】解:由题知△ABD≌△ACE,故BD与CE,AB与AC,AD与AE;对应角是∠B与∠C,∠ADB与∠ACE,∠BAD与∠CAE。
【典例 2】【变式训练】D
达标训练·夯基础
知识点一
1.B 2.A 3.C
4.解:由△ABC≌△BAD知:点A与点B、点B与点A、点C与点D,分别是对应点,因此AB与BA,AC与BD,BC与AD分别是对应边;∠ABC与∠BAD,∠BAC与∠ABD,∠C与∠D分别是对应角。
知识点二
1.A 2.B 3.B 4.100
5.解:(1)因为△ABC≌△ADE,所以BC=DE,AC=AE,AB=AD,∠BAC=∠DAE,∠B=∠D,∠C=∠E。
(2)∠1=∠2.理由:由(1)得∠BAC=∠DAE,即∠1+∠DAC=∠2+∠DAC,所以∠1=∠2.
纠错:本题只注意了全等三角形的对应边相等,遗漏了图形中隐含的相等线段BE=CF
考题变式·提能力
解:因为△ABC≌△A’B’C’,所以∠C=∠C’=24o,所以∠B=180o-∠A-∠C=180o-36o-24o=120o。
答案:120o
【母题变式】解:因为△ABC≌△A’B’C’,所以∠C’=∠C,所以∠C’=∠C=180o-∠A-∠B=
180o-36o-120o=24o,
答案:24o
新知识记:
1.全等图形
(1)定义:能够 的两个图形。
(2)特点: 和 都相同。
2.全等三角形
(1)定义:能够 的两个三角形。
(2)对应元素:
① 的顶点叫做对应顶点;
② 的边叫做对应边;
③ 的角叫做对应角。
(3)表示方法:
①表示:△ABC和△DEF全等,记作△ABC △DEF;
②注意:记两个三角形全等时,把表示对应顶点的字母写在 位置上。
(4)性质:
①全等三角形的对应边 ;
②全等三角形的对应角 。
知识点一 全等形、全等三角形的有关概念
【典例 1】如图,已知△ABE和△ACD全等,∠ADE = ∠AED,∠B = ∠C,指出全等三 A
角形中其他的对应边和对应角。
【规范解答】因为∠B = ∠C,∠ADE = ∠AED,所以∠B与∠C,
∠ADE与∠AED分别是△ABE和△ACD的对应角,
所以∠BAE与∠CAD是对应角;(全等三角形对应角的概念) B D E C
所以AB与AC,AE与AD,BE与CD分别是对应边。(全等三角形对应边的概念)
【变式训练】
如图,已知△ABD和△ACE全等,∠B = ∠C,BD与CE是对应边,指出全等 A
三角形中的对应边和对应角。
B D E C
知识点二 全等三角形的性质的应用
【典例 2】如图,点A,B,C在同一直线上,点E在BD上,且△ABD≌△EBC,AB = 2 cm,BC = 3 cm。
(1)求DE的长。 D
(2)判断BD与AC的位置关系,并说明理由。
E
【规范解答】(1)因为△ABD≌△EBC,
所以BD = BC = 3 cm,BE=AB=2cm,(全等三角 A B C
形对应边相等)
DE=BD-BE=1cm。(线段的和差)
(2)BD与AC垂直。
理由:因为△ABD≌△EBC,所以∠ABD=∠EBC,(全等三角形的对应角相等)
又因为A,B,C在一条直线上,
所以∠ABC=180°,(平角定义)
又∠ABD=∠EBC,∠EBC=90°,
所以BD与AC垂直。(垂直定义)
【变式训练】如图,△ABC ≌ △EBD,AB = 3 cm,AD = 8 cm,则CE的长度为( )
A.3 cm B.5 cm C.8 cm D.2 cm C
E
A B D
达标训练·夯基础
知识点一 全等形、全等三角形的有关概念
1.下图中,全等的图形有( )
A.2组 B.3组 C.4组 D.5组
2.如图,点E,F在线段BC上,△ABF与△DCE全等,点A与 A D
点D,点B与点C是对应顶点,AF与DE交于点M, M
则∠DCE = ( ) B E F C
A. ∠ B B. ∠ A C. ∠ EMF D. ∠ AFB B
3.如图所示,将△ABC沿AC翻折,则图中全等三角形有( ) A D C
A.1对 B.2对 C.3对 D.4对
E
4.如图,已知△ABC≌△BAD,从中找出这两个全等三角形的对应边和对应角。
C D
O
A B
知识点二 全等三角形的性质的应用
1.如图,Rt△ABC≌Rt△DEF,∠B=60o,则∠D的度数为( )
A F
E
B C D
A.30o B.45o C.60o D.90o
2.(2018·广州期中)如图,△ABC≌△ADE,若∠BAE=120o,∠BAD=40o,则∠BAC的度数为( )
A.40o B.80o C.120o D.无法确定 A E
B D C
3.如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( ) A
A.2 B.3 C.5 D.2.5
F E
B C
4.如图所示,△ABD是△ABC沿AB边所在的直线翻折得到的, C
已知∠C=100o,∠ABC=30o,则∠CAD= 度。
A B
D
5.如图,已知△ABC≌△ADE。 A
(1)写出这两个三角形中相等的边和角。
(2)∠BAD与∠EAC相等吗?说明理由。 E
B D C
纠错: A D
如图,△ABC≌△DEF,则此图中相等的线段有( )
A.1对 B.2对 C.3对 D.4对
B E C F
解:选C 因为△ABC≌△DEF
所以AB=DE,AC=DF,BC=EF,那有3对线段的线段。
错因:
考题变式·提能力
(2016·成都中考)如图,△ABC≌△A’B’C’,其中∠A=36o,∠C’=24o,则∠B= 。
A A’
B B’
C C’
母题变式
如图,△ABC≌△A’B’C’,其中∠A=36o,∠B=120o,则∠C’= 。
A A’
B B’
C C’
参考答案及解析
新知识记:
(1)完全重合 (2)形状 大小
(1)完全重合 (2)①重合 ②重合 ③重合 (3)①≌ ②对应
①相等 ②相等
典例精析·拓新知
【典例 1】【变式训练】解:由题知△ABD≌△ACE,故BD与CE,AB与AC,AD与AE;对应角是∠B与∠C,∠ADB与∠ACE,∠BAD与∠CAE。
【典例 2】【变式训练】D
达标训练·夯基础
知识点一
1.B 2.A 3.C
4.解:由△ABC≌△BAD知:点A与点B、点B与点A、点C与点D,分别是对应点,因此AB与BA,AC与BD,BC与AD分别是对应边;∠ABC与∠BAD,∠BAC与∠ABD,∠C与∠D分别是对应角。
知识点二
1.A 2.B 3.B 4.100
5.解:(1)因为△ABC≌△ADE,所以BC=DE,AC=AE,AB=AD,∠BAC=∠DAE,∠B=∠D,∠C=∠E。
(2)∠1=∠2.理由:由(1)得∠BAC=∠DAE,即∠1+∠DAC=∠2+∠DAC,所以∠1=∠2.
纠错:本题只注意了全等三角形的对应边相等,遗漏了图形中隐含的相等线段BE=CF
考题变式·提能力
解:因为△ABC≌△A’B’C’,所以∠C=∠C’=24o,所以∠B=180o-∠A-∠C=180o-36o-24o=120o。
答案:120o
【母题变式】解:因为△ABC≌△A’B’C’,所以∠C’=∠C,所以∠C’=∠C=180o-∠A-∠B=
180o-36o-120o=24o,
答案:24o
