1.2 矩形的性质与判定优化练习设计(含原题版解析版)
文档属性
| 名称 | 1.2 矩形的性质与判定优化练习设计(含原题版解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-16 00:00:00 | ||
图片预览


文档简介
【新北师大版九年级数学(上)同步练习】
§1.2《矩形的性质与判定》(原题版)
一.选择题:(每小题5分,共25分)
1. 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
A. 四边形ABCD由矩形变为平行四边形 B. BD的长度增大
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
2. 如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A. ∠ABC=90° B. AC=BD C. OA=OB D. OA=AD
3.如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
A. 30° B. 45° C. 60° D. 75°
4. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
A. (3,1) B. (3,) C. (3,) D. (3,2)
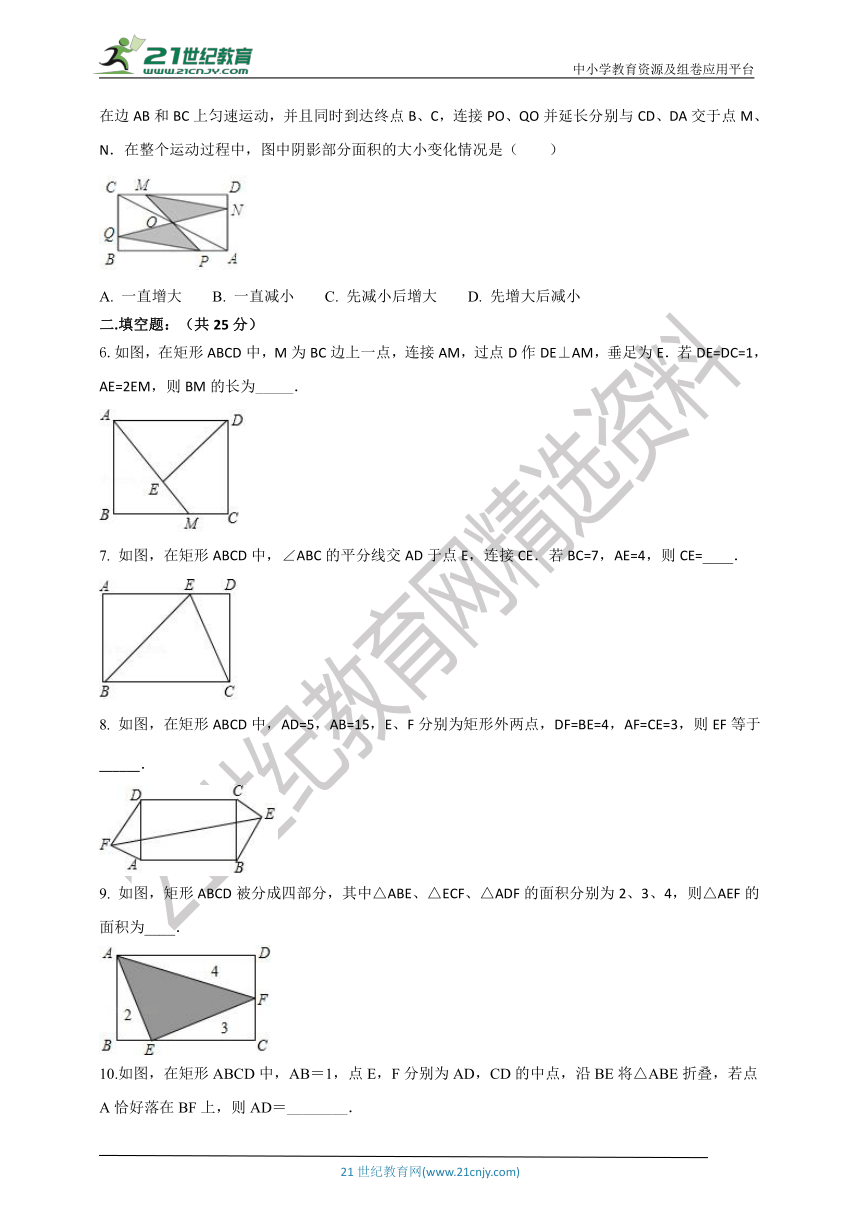
5.如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )
A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
二.填空题:(共25分)
6.如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为_____.
7. 如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=____.
8. 如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE=4,AF=CE=3,则EF等于______.
9. 如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为____.
10.如图,在矩形ABCD中,AB=1,点E,F分别为AD,CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=________.
三.解答题:(共50分)
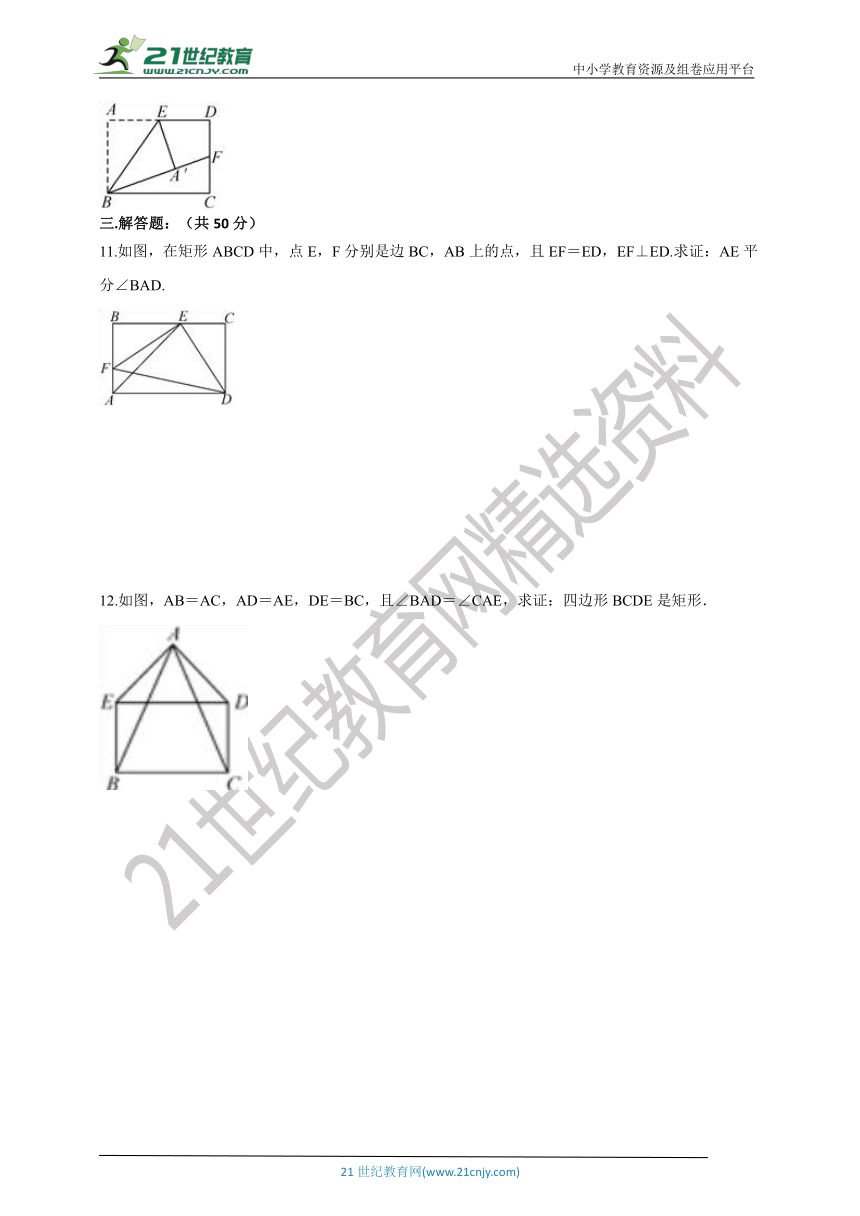
11.如图,在矩形ABCD中,点E,F分别是边BC,AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.
12.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE,求证:四边形BCDE是矩形.
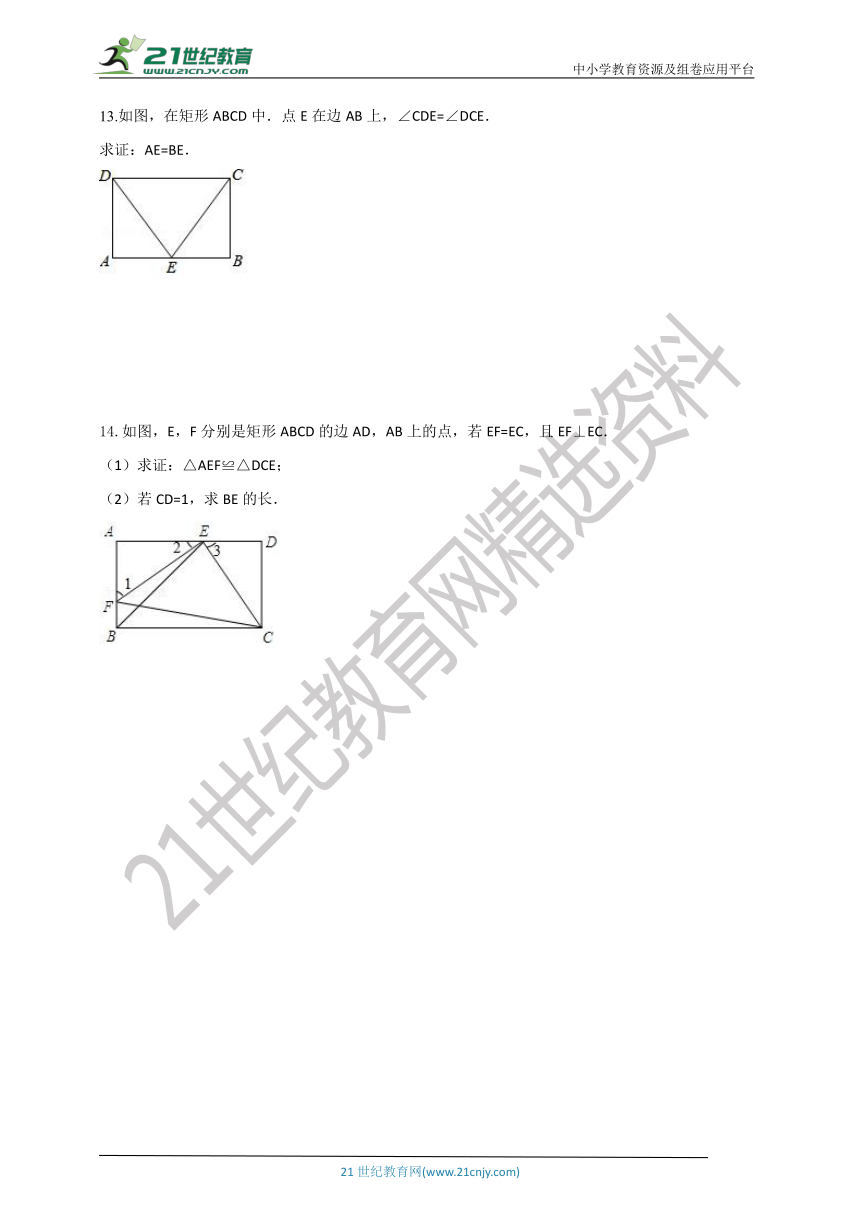
13.如图,在矩形ABCD中.点E在边AB上,∠CDE=∠DCE.
求证:AE=BE.
14.如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
15.如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.
(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形
1.2《矩形的性质与判定》(解析版)
一.选择题:(每小题5分,共25分)
1. 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
A. 四边形ABCD由矩形变为平行四边形
B. BD的长度增大
C. 四边形ABCD的面积不变
D. 四边形ABCD的周长不变
【答案】C
【解析】试题分析:由题意可知,当向右扭动框架时,BD可伸长,故BD的长度变大,四边形ABCD由矩形变为平行四边形 ,因为四条边的长度不变,所以四边形ABCD的周长不变.原来矩形ABCD的面积等于BC乘以AB,变化后平行四边形ABCD的面积等于底乘以高,即BC乘以BC边上的高,BC边上的高小于AB,所以四边形ABCD的面积变小了,故A,B,D说法正确,C说法错误.故正确的选项是C.
考点:1.四边形面积计算;2.四边形的不稳定性.
2. 如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A. ∠ABC=90° B. AC=BD C. OA=OB D. OA=AD
【答案】D
【解析】试题分析:本题考查了矩形的性质;熟练掌握矩形的性质是解决问题的关键.矩形的性质:四个角都是直角,对角线互相平分且相等;由矩形的性质容易得出结论.∵四边形ABCD是矩形,∴∠ABC=∠BCD=∠CDA=∠BAD=90°,AC=BD,OA=AC,OB=BD,∴OA=OB,∴A、B、C正确,D错误
3.如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
A. 30° B. 45° C. 60° D. 75°
【答案】C
【解析】如图所示:
由题意可得:∠1=∠2,AN=MN,∠MGA=90°,
则NG=AM,故AN=NG,
则∠2=∠4,
∵EF∥AB,
∴∠4=∠3,
∴∠1=∠2=∠3=×90°=30°,
∴∠DAG=60°.
故选:C.
4. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
A. (3,1) B. (3,) C. (3,) D. (3,2)
【答案】B
【解析】试题分析:如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,根据D为(,0),A(3,0)可得H为( ,0),可得直线CH的解析式为,把x=3代入即可求得y=,从而求得点E的坐标为(3,).
故选:B.
5.如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )
A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
【答案】C
【解析】连接OB,根据点O是为对角线AC的中点可得△ABO和△BOC的面积相等,又点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,然后把开始时、结束时、与中点时的△OPQ的面积与△ABC的面积相比即可进行判断.
解:如图所示,
连接OB,∵O是AC的中点, ∴S△ABO=S△BOC=S△ABC, 开始时,S△OBP=S△AOB=S△ABC, 点P到达AC的中点时,点Q到达BC的中点时,S△OPQ=S△ABC, 结束时,S△OPQ=S△BOC=S△ABC, 所以,图中阴影部分面积的大小变化情况是:先减小后增大. 故选C.
二.填空题:(共25分)
6.如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为_____.
【答案】
【解析】试题解析:∵四边形ABCD是矩形,
∴∠AMB=∠DAE,
∵DE=DC,
∴AB=DE,
∵DE⊥AM,
在△ABM和△DEA中,
∴AM=AD,
∵AE=2EM,
∴BC=AD=3EM,
连接DM,如图所示:
在和中,
∴EM=CM,
∴BC=3CM,
设EM=CM=x,则BM=2x,AM=BC=3x,
在中,由勾股定理得: 解得:x=,
∴BM=;
故答案为:.
7. 如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=____.
【答案】5
【解析】∵四边形ABCD是矩形,∴AD∥BC,AD=BC,AB=CD,∠D=90°.
∴∠AEB=∠CBE.
∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠ABE=∠AEB,∴AE=AB.
∴CD=AE=4,DE=AD-AE=BC-AE=7-4=3.
在Rt△CDE中,根据勾股定理得CE=.
故答案为5.
8. 如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE=4,AF=CE=3,则EF等于______.
【答案】
【解析】由题意得: 都是直角三角形.
,
9. 如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为____.
【答案】7
【解析】试题解析:设AB=a,BC=b,
∵△CEF,△ABE,△ADF的面积分别是2,3,4,
∴S△ABE=×a×BE=2,
∴BE=,
∴EC=BC-BE=b-,
∵S△CEF=×EC×FC=3,
∴FC=,
∴DF=CD-CF=a-,
∴S△ADF=×(a-)×b=4,
∴(ab)2-18ab+32=0,
解得:ab=16或ab=2(不合题意,舍去),
∴S△AEF=16-3-4-2=7
10.如图,在矩形ABCD中,AB=1,点E,F分别为AD,CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=________.
【答案】
【解析】试题分析:连接EF,则可证明△EA′F≌△EDF,从而根据BF=BA′+A′F,得出BF的长,在Rt△BCF中,利用勾股定理可求出BC,即得AD的长度.
解:连接EF,
∵点E、点F是AD、DC的中点,
∴AE=ED,CF=DF=CD=AB=,
由折叠的性质可得AE=A′E,
∴A′E=DE,
在Rt△EA′F和Rt△EDF中,
∵,
∴Rt△EA′F≌Rt△EDF(HL),
∴A′F=DF=,
∴BF=BA′+A′F=AB+DF=1+=,
在Rt△BCF中,BC==.
∴AD=BC=.
故答案为:.
三.解答题:(共50分)
11.如图,在矩形ABCD中,点E,F分别是边BC,AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.
【答案】证明见解析.
【解析】要证AE平分∠BAD,可转化为△ABE为等腰直角三角形,得AB=BE,又AB=CD,再将它们分别转化为两全等三角形的两对应边,根据全等三角形的判定,和矩形的性质,可确定ASA.即求证.
证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,AB=CD,
∴∠BEF+∠BFE=90°.
∵EF⊥ED,
∴∠BEF+∠CED=90°.
∴∠BFE=∠CED.
∴∠BEF=∠EDC.
又∵EF=ED,
∴△EBF≌△DCE.
∴BE=CD.
∴BE=AB.∴∠BAE=∠BEA=45°.
∴∠EAD=45°.
∴∠BAE=∠EAD.
∴AE平分∠BAD.
12.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE,求证:四边形BCDE是矩形.
【答案】证明见解析.
【解析】试题分析:求出∠BAE=∠CAD,证△BAE≌△CAD,推出∠BEA=∠CDA,BE=CD,得出平行四边形BCDE,根据平行线性质得出∠BED+∠CDE=180°,求出∠BED,根据矩形的判定求出即可.
试题解析:∵∠BAD=∠CAE,
∴∠BAD-∠BAC=∠CAE-∠BAC,
∴∠BAE=∠CAD,
∵在△BAE和△CAD中
∴△BAE≌△CAD(SAS),
∴∠BEA=∠CDA,BE=CD,
∵DE=CB,
∴四边形BCDE是平行四边形,
∵AE=AD,
∴∠AED=∠ADE,
∵∠BEA=∠CDA,
∴∠BED=∠CDE,
∵四边形BCDE是平行四边形,
∴BE∥CD,
∴∠CDE+∠BED=180°,
∴∠BED=∠CDE=90°,
∴四边形BCDE是矩形.
13.如图,在矩形ABCD中.点E在边AB上,∠CDE=∠DCE.
求证:AE=BE.
【答案】证明见解析
【解析】试题分析:
因为∠CDE=∠DCE,所以ED=EC,则可用HL证明Rt△DAE≌Rt△CBE,从而得AE=BE.
试题解析:
∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵∠CDE=∠DCE,
∴DE=CE,
在Rt△DAE和Rt△CBE中,,
∴Rt△DAE≌Rt△CBE(HL),
∴AE=BE.
14.如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
【答案】(1)证明见解析(2)
【解析】试题分析:(1)根据矩形的性质和已知条件可证明△AEF≌△DCE;
(2)由(1)可知AE=DC,在Rt△ABE中由勾股定理可求得BE的长
试题解析:(1)证明:在矩形ABCD中,∠A=∠D=90°,
∴∠1+∠2=90°,
∵EF⊥EC,
∴∠FEC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
在△AEF和△DCE中,
,
∴△AEF≌△DCE(AAS)
(2)解:由(1)知△AEF≌△DCE,
∴ AE=DC=1,
在矩形ABCD中,AB=CD=1,
在R△ABE中,AB2+AE2=BE2,即12+12=BE2,∴BE=.
15.如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.
(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)易证得△AEH≌△CGF,从而证得BE=DG,DH=BF.故有,△BEF≌△DGH,根据两组对边分别相等的四边形是平行四边形而得证.
(2)由题意知,平行四边形ABCD是菱形,连接AC,BD,则有AC⊥BD,由AB=AD,且AH=AE可证得HE∥BD,同理可得到HG∥AC,故HG⊥HE,又由(1)知四边形HGFE是平行四边形,故四边形HGFE是矩形.
试题解析:证明:(1)在平行四边形ABCD中,∠A=∠C,
又∵AE=CG,AH=CF,
∴△AEH≌△CGF.
∴EH=GF.
在平行四边形ABCD中,AB=CD,AD=BC,
∴AB-AE=CD-CG,AD-AH=BC-CF,
即BE=DG,DH=BF.
又∵在平行四边形ABCD中,∠B=∠D,
∴△BEF≌△DGH.
∴GH=EF.
∴四边形EFGH是平行四边形.
(2)在平行四边形ABCD中,AB∥CD,AB=CD.
设∠A=α,则∠D=180°-α.
∵AE=AH,∴∠AHE=∠AEH=.
∵AD=AB=CD,AH=AE=CG,
∴AD-AH=CD-CG,即DH=DG.
∴∠DHG=∠DGH=.
∴∠EHG=180°-∠DHG-∠AHE=90°.
又∵四边形EFGH是平行四边形,
∴四边形EFGH是矩形.
§1.2《矩形的性质与判定》(原题版)
一.选择题:(每小题5分,共25分)
1. 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
A. 四边形ABCD由矩形变为平行四边形 B. BD的长度增大
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
2. 如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A. ∠ABC=90° B. AC=BD C. OA=OB D. OA=AD
3.如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
A. 30° B. 45° C. 60° D. 75°
4. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
A. (3,1) B. (3,) C. (3,) D. (3,2)
5.如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )
A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
二.填空题:(共25分)
6.如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为_____.
7. 如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=____.
8. 如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE=4,AF=CE=3,则EF等于______.
9. 如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为____.
10.如图,在矩形ABCD中,AB=1,点E,F分别为AD,CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=________.
三.解答题:(共50分)
11.如图,在矩形ABCD中,点E,F分别是边BC,AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.
12.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE,求证:四边形BCDE是矩形.
13.如图,在矩形ABCD中.点E在边AB上,∠CDE=∠DCE.
求证:AE=BE.
14.如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
15.如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.
(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形
1.2《矩形的性质与判定》(解析版)
一.选择题:(每小题5分,共25分)
1. 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
A. 四边形ABCD由矩形变为平行四边形
B. BD的长度增大
C. 四边形ABCD的面积不变
D. 四边形ABCD的周长不变
【答案】C
【解析】试题分析:由题意可知,当向右扭动框架时,BD可伸长,故BD的长度变大,四边形ABCD由矩形变为平行四边形 ,因为四条边的长度不变,所以四边形ABCD的周长不变.原来矩形ABCD的面积等于BC乘以AB,变化后平行四边形ABCD的面积等于底乘以高,即BC乘以BC边上的高,BC边上的高小于AB,所以四边形ABCD的面积变小了,故A,B,D说法正确,C说法错误.故正确的选项是C.
考点:1.四边形面积计算;2.四边形的不稳定性.
2. 如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A. ∠ABC=90° B. AC=BD C. OA=OB D. OA=AD
【答案】D
【解析】试题分析:本题考查了矩形的性质;熟练掌握矩形的性质是解决问题的关键.矩形的性质:四个角都是直角,对角线互相平分且相等;由矩形的性质容易得出结论.∵四边形ABCD是矩形,∴∠ABC=∠BCD=∠CDA=∠BAD=90°,AC=BD,OA=AC,OB=BD,∴OA=OB,∴A、B、C正确,D错误
3.如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
A. 30° B. 45° C. 60° D. 75°
【答案】C
【解析】如图所示:
由题意可得:∠1=∠2,AN=MN,∠MGA=90°,
则NG=AM,故AN=NG,
则∠2=∠4,
∵EF∥AB,
∴∠4=∠3,
∴∠1=∠2=∠3=×90°=30°,
∴∠DAG=60°.
故选:C.
4. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
A. (3,1) B. (3,) C. (3,) D. (3,2)
【答案】B
【解析】试题分析:如图,作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,根据D为(,0),A(3,0)可得H为( ,0),可得直线CH的解析式为,把x=3代入即可求得y=,从而求得点E的坐标为(3,).
故选:B.
5.如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )
A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
【答案】C
【解析】连接OB,根据点O是为对角线AC的中点可得△ABO和△BOC的面积相等,又点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,然后把开始时、结束时、与中点时的△OPQ的面积与△ABC的面积相比即可进行判断.
解:如图所示,
连接OB,∵O是AC的中点, ∴S△ABO=S△BOC=S△ABC, 开始时,S△OBP=S△AOB=S△ABC, 点P到达AC的中点时,点Q到达BC的中点时,S△OPQ=S△ABC, 结束时,S△OPQ=S△BOC=S△ABC, 所以,图中阴影部分面积的大小变化情况是:先减小后增大. 故选C.
二.填空题:(共25分)
6.如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为_____.
【答案】
【解析】试题解析:∵四边形ABCD是矩形,
∴∠AMB=∠DAE,
∵DE=DC,
∴AB=DE,
∵DE⊥AM,
在△ABM和△DEA中,
∴AM=AD,
∵AE=2EM,
∴BC=AD=3EM,
连接DM,如图所示:
在和中,
∴EM=CM,
∴BC=3CM,
设EM=CM=x,则BM=2x,AM=BC=3x,
在中,由勾股定理得: 解得:x=,
∴BM=;
故答案为:.
7. 如图,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE.若BC=7,AE=4,则CE=____.
【答案】5
【解析】∵四边形ABCD是矩形,∴AD∥BC,AD=BC,AB=CD,∠D=90°.
∴∠AEB=∠CBE.
∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠ABE=∠AEB,∴AE=AB.
∴CD=AE=4,DE=AD-AE=BC-AE=7-4=3.
在Rt△CDE中,根据勾股定理得CE=.
故答案为5.
8. 如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE=4,AF=CE=3,则EF等于______.
【答案】
【解析】由题意得: 都是直角三角形.
,
9. 如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为____.
【答案】7
【解析】试题解析:设AB=a,BC=b,
∵△CEF,△ABE,△ADF的面积分别是2,3,4,
∴S△ABE=×a×BE=2,
∴BE=,
∴EC=BC-BE=b-,
∵S△CEF=×EC×FC=3,
∴FC=,
∴DF=CD-CF=a-,
∴S△ADF=×(a-)×b=4,
∴(ab)2-18ab+32=0,
解得:ab=16或ab=2(不合题意,舍去),
∴S△AEF=16-3-4-2=7
10.如图,在矩形ABCD中,AB=1,点E,F分别为AD,CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=________.
【答案】
【解析】试题分析:连接EF,则可证明△EA′F≌△EDF,从而根据BF=BA′+A′F,得出BF的长,在Rt△BCF中,利用勾股定理可求出BC,即得AD的长度.
解:连接EF,
∵点E、点F是AD、DC的中点,
∴AE=ED,CF=DF=CD=AB=,
由折叠的性质可得AE=A′E,
∴A′E=DE,
在Rt△EA′F和Rt△EDF中,
∵,
∴Rt△EA′F≌Rt△EDF(HL),
∴A′F=DF=,
∴BF=BA′+A′F=AB+DF=1+=,
在Rt△BCF中,BC==.
∴AD=BC=.
故答案为:.
三.解答题:(共50分)
11.如图,在矩形ABCD中,点E,F分别是边BC,AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.
【答案】证明见解析.
【解析】要证AE平分∠BAD,可转化为△ABE为等腰直角三角形,得AB=BE,又AB=CD,再将它们分别转化为两全等三角形的两对应边,根据全等三角形的判定,和矩形的性质,可确定ASA.即求证.
证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,AB=CD,
∴∠BEF+∠BFE=90°.
∵EF⊥ED,
∴∠BEF+∠CED=90°.
∴∠BFE=∠CED.
∴∠BEF=∠EDC.
又∵EF=ED,
∴△EBF≌△DCE.
∴BE=CD.
∴BE=AB.∴∠BAE=∠BEA=45°.
∴∠EAD=45°.
∴∠BAE=∠EAD.
∴AE平分∠BAD.
12.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE,求证:四边形BCDE是矩形.
【答案】证明见解析.
【解析】试题分析:求出∠BAE=∠CAD,证△BAE≌△CAD,推出∠BEA=∠CDA,BE=CD,得出平行四边形BCDE,根据平行线性质得出∠BED+∠CDE=180°,求出∠BED,根据矩形的判定求出即可.
试题解析:∵∠BAD=∠CAE,
∴∠BAD-∠BAC=∠CAE-∠BAC,
∴∠BAE=∠CAD,
∵在△BAE和△CAD中
∴△BAE≌△CAD(SAS),
∴∠BEA=∠CDA,BE=CD,
∵DE=CB,
∴四边形BCDE是平行四边形,
∵AE=AD,
∴∠AED=∠ADE,
∵∠BEA=∠CDA,
∴∠BED=∠CDE,
∵四边形BCDE是平行四边形,
∴BE∥CD,
∴∠CDE+∠BED=180°,
∴∠BED=∠CDE=90°,
∴四边形BCDE是矩形.
13.如图,在矩形ABCD中.点E在边AB上,∠CDE=∠DCE.
求证:AE=BE.
【答案】证明见解析
【解析】试题分析:
因为∠CDE=∠DCE,所以ED=EC,则可用HL证明Rt△DAE≌Rt△CBE,从而得AE=BE.
试题解析:
∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵∠CDE=∠DCE,
∴DE=CE,
在Rt△DAE和Rt△CBE中,,
∴Rt△DAE≌Rt△CBE(HL),
∴AE=BE.
14.如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
【答案】(1)证明见解析(2)
【解析】试题分析:(1)根据矩形的性质和已知条件可证明△AEF≌△DCE;
(2)由(1)可知AE=DC,在Rt△ABE中由勾股定理可求得BE的长
试题解析:(1)证明:在矩形ABCD中,∠A=∠D=90°,
∴∠1+∠2=90°,
∵EF⊥EC,
∴∠FEC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
在△AEF和△DCE中,
,
∴△AEF≌△DCE(AAS)
(2)解:由(1)知△AEF≌△DCE,
∴ AE=DC=1,
在矩形ABCD中,AB=CD=1,
在R△ABE中,AB2+AE2=BE2,即12+12=BE2,∴BE=.
15.如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.
(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)易证得△AEH≌△CGF,从而证得BE=DG,DH=BF.故有,△BEF≌△DGH,根据两组对边分别相等的四边形是平行四边形而得证.
(2)由题意知,平行四边形ABCD是菱形,连接AC,BD,则有AC⊥BD,由AB=AD,且AH=AE可证得HE∥BD,同理可得到HG∥AC,故HG⊥HE,又由(1)知四边形HGFE是平行四边形,故四边形HGFE是矩形.
试题解析:证明:(1)在平行四边形ABCD中,∠A=∠C,
又∵AE=CG,AH=CF,
∴△AEH≌△CGF.
∴EH=GF.
在平行四边形ABCD中,AB=CD,AD=BC,
∴AB-AE=CD-CG,AD-AH=BC-CF,
即BE=DG,DH=BF.
又∵在平行四边形ABCD中,∠B=∠D,
∴△BEF≌△DGH.
∴GH=EF.
∴四边形EFGH是平行四边形.
(2)在平行四边形ABCD中,AB∥CD,AB=CD.
设∠A=α,则∠D=180°-α.
∵AE=AH,∴∠AHE=∠AEH=.
∵AD=AB=CD,AH=AE=CG,
∴AD-AH=CD-CG,即DH=DG.
∴∠DHG=∠DGH=.
∴∠EHG=180°-∠DHG-∠AHE=90°.
又∵四边形EFGH是平行四边形,
∴四边形EFGH是矩形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
