1.3 探索三角形全等的条件同步练习(第3课时)
文档属性
| 名称 | 1.3 探索三角形全等的条件同步练习(第3课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 990.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-17 08:13:43 | ||
图片预览



文档简介
3 探索三角形全等的条件(第3课时)
新知识记:
1.判定三角形全等是方法(4)
两边及其 分别相等的两个三角形全等,(简写成“ ”或“ ”)。
2.应用格式
如图所示:
AB=DE
在△ABC与△DEF中 所以△ABC△ABC与△DEF△DEF(SAS)
AC=DF
3.全等三角形对应的中线、角平分线、高线、面积等都 。
典例精析·拓新知
知识点一 应用“SAS"证明三角形全等
【典例1】(2017·南充中考)如图,DE⊥AB,CF⊥AB,垂足分别是点E,F,DE=CF,AE=BF。试说明:AC∥BD
【规范解答】因为AE=BF 所以AE+EF=BF+EF,即AF=BE
………等量加等量和相等
因为DE⊥AB,CF⊥AB,所以∠AFC=∠BED=90°………垂直定义
在△AFC和△BED中:AF = BE,∠AFC=∠BED,CF=DE,
所以△AFC≌△BED.(SAS)
所以∠A=∠B…………全等三角形的对应角相等
所以AC∥BD.…………内错角相等,两直线平行
学霸提醒:
应用“SAS"判定两个三角形全等的“两点注意”
1.对应:“SAS”包含“边”“角”两种元素,一定要注意元素的“对应”关系。
2.顺序:在应用时一定要按边→角→边的顺序排列条件,绝不能出现边→边→角(或角→边一边)的错误,因为边边角(或角边边)不能保证两个三角形全等。
【变式训练】如图,DE⊥AB,CF⊥AB,垂足分别是 E,F,DE=CF,AE=BF.试说明:AC=BD。
知识点二 三角形全等判定方法的综合应用
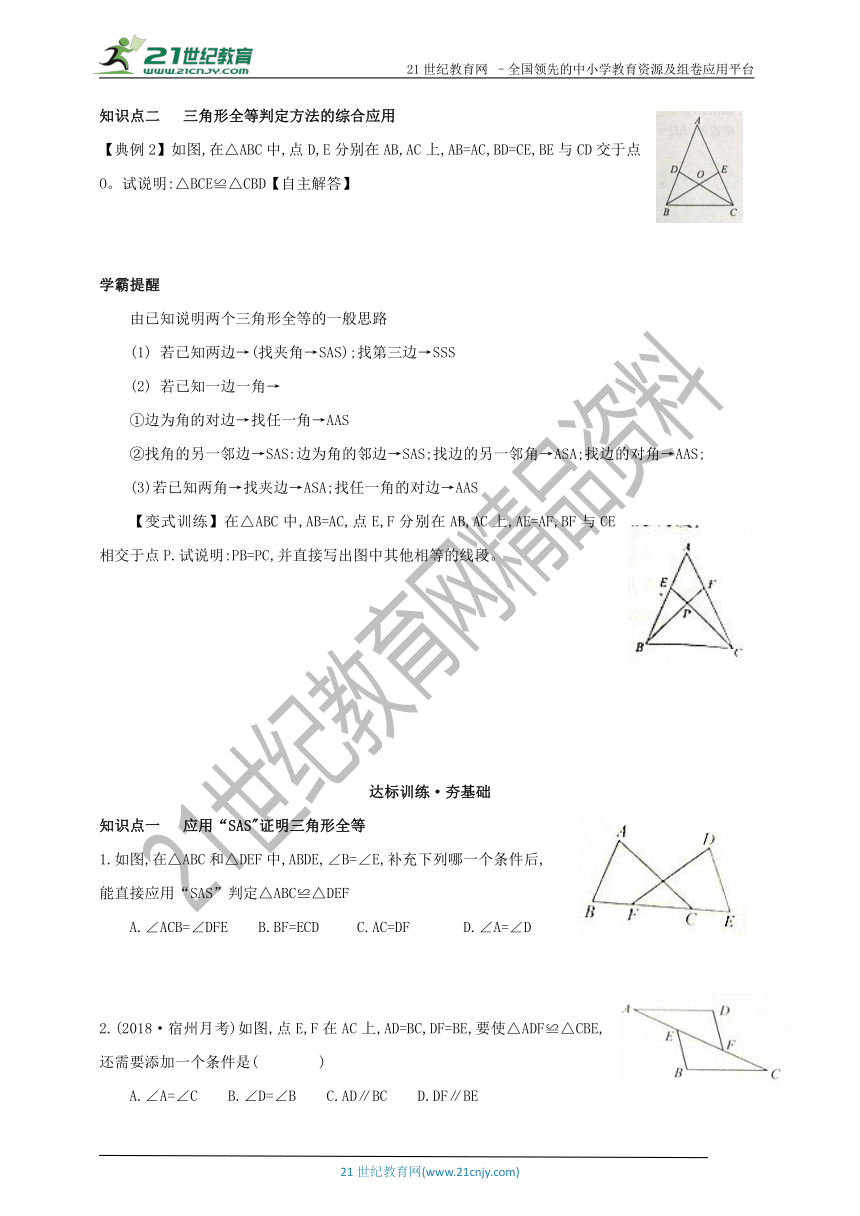
【典例2】如图,在△ABC中,点D,E分别在AB,AC上,AB=AC,BD=CE,BE与CD交于点O。试说明:△BCE≌△CBD【自主解答】
学霸提醒
由已知说明两个三角形全等的一般思路
若已知两边→(找夹角→SAS);找第三边→SSS
若已知一边一角→
①边为角的对边→找任一角→AAS
②找角的另一邻边→SAS:边为角的邻边→SAS;找边的另一邻角→ASA;找边的对角→AAS;
(3)若已知两角→找夹边→ASA;找任一角的对边→AAS
【变式训练】在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.试说明:PB=PC,并直接写出图中其他相等的线段。
达标训练·夯基础
知识点一 应用“SAS"证明三角形全等
1.如图,在△ABC和△DEF中,ABDE,∠B=∠E,补充下列哪一个条件后,
能直接应用“SAS”判定△ABC≌△DEF
A.∠ACB=∠DFE B.BF=ECD C.AC=DF D.∠A=∠D
2.(2018·宿州月考)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
A.∠A=∠C B.∠D=∠B C.AD∥BC D.DF∥BE
3.如图,AD和CB相交于点E,BE=DE,请添加一个条件,能利用“SAS”判定△ABE≌△CDE(只添加一个条件即可),你所添加的条件是 。
如图,AB是∠DAC的平分线,且AD=AC.试说明:BD=BC。
5.(2017·吉林中考)如图,点E,F在BC上,BE=FC,AB=DC,∠B=∠C.试说明:∠A=∠D。
知识点二 三角形全等判定方法的综合应用
1.(2018·德州乐陵期中)下列条件中不能判定△ABC≌△DEF的是( )
A.AB=DE, AC=DF, BC=EF B.AB=DE,∠A=∠D,BC=EF
C.AB=DE,∠B=∠DEF,BC=EF D.∠B=∠DEF,∠A=∠D,AB=DE
2.(2018·诸暨市期中)如图(1),已知△ABC的六个元素,则图(2)、图(3)、图(4)中的三角形和△ABC全等的有( )
A.图(2)和图(3)
B.图(3)和图(4)
C.只有图(3)
D.只有图(4)
(2018·常德模拟)如图,点P在∠AOB的平分线上,若使△AOP0≌△BOP,
则需添加的一个条件是 (只写一个即可,不添加辅助线)
4.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2
(1)试说明:BD=CE.
(2)试说明:∠M=∠N.
纠错园
如图,AC,BD相交于点E.∠D=∠C,AD=BC,
试说明:△ABD≌△BAC
解:在△ABD和△BAC中
因为AD=BC ∠D=∠C, AB=BA
所以△ABD≌△BAC(SAS)
【错因】
考题变式·提能力
(2017·郴州中考)已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB,AC的中点.
试说明:BE=CD
母题变式
【变式一】在△ABC中,AB=AC,点E,F分别在 AB,AC上,AE=AF,∠ABC=∠ACB,
BF与CE相交于点P。
试说明:△EBC≌△FCB。
【变式二】如图,点D,E分别是AB,AC上的点,且AB=AC,AD=AE.试说明:∠B=∠C。
【变式三】如图,AB=AC,点E,F分别是AB,AC的点.试说明:△AFB≌△AEC。
参考答案及解析
新知识记
1.夹角 边角边 SAS 2.∠A=∠D 3.相等
典例精析·拓新知
【典例1】【变式训练】
解:因为AE=BF,所以AE+EF=BF+EF,即AF=BE
因为DE⊥AB,CF⊥AB,所以∠AFC=∠BED=90o
在△AFC和△BED中 :AF=BE,∠AFC=∠BED,CF=DE,所以AFC≌△BED(SAS).所以AC=DE。
【典例2】【自主解答】因为AB=AC,BD=CE,所以AB-BD=AC-CE,即AD=AB=AC,∠BAE=∠CAD,AE=AD,
所以△ABE≌△ACD(SAS),所以DC=BE,在△DBC与△ECB中,DB=EC,DC=EB. BC=CB,
所以△BCE≌△CBD(SSS)
【变式训练】解:在△ABF和△ACE中:AB=AC,∠BAF=∠CAE,AF=AE, 所以△ABF≌△ACE(SAS)
所以∠ABF=∠ACE(全等三角形的对应角相等) BF=CE(全等三角形的对应边相等)
因为AB=AC,AE=AF,所以BE=CF,在△BEP和△CFP中: ∠BPE=∠CPF,∠PBE=∠PCF,BE =CF
所以△BEP≌△CFP(AAS),所以PB=PC,因为BF=CE所以PE=PF,所以图中相等的线段为PE=PF,BF=CE。
达标训练·夯基础
1.B 2.B 3. AE=CE
4.解:因为AB是∠DAC的平分线,所以∠DAB=∠BAC,在△DAB和△CAB中,AD=AC,∠DAB=∠CAB,AB=AB,所以△DAB≌△CAB(SAS),所以BD=BC
5.解:因为BE=FC,所以BE+EF=CF+EF;又因为AB=DC,∠B=∠C,所以△ABF≌△DCE(SAS),
所以∠A=∠D。
知识点二
1.B 2.D
3.OA=OB(或∠OAP=∠OBP或∠OPA=∠OPB.答案不唯一)
4.解:(1)在△ABD和△ACE中,AB=AC,∠1=∠2,AD=AE,所以△ABD≌△ACE(SAS)所以BD=CE。
(2)因为∠1=∠2,所以∠1+∠DAE=∠2+∠DAE即∠BAN=∠CAM
由(1)得△ABD≌△ACE,所以∠B=∠C,在△ACM和△ABN中:∠C=∠B,AC=AB,∠CAM=∠BAN,
所以△ACM≌△ABN(ASA)所以∠M=∠N
【纠错园】
根据条件不能直接利用SAS判定△ABD和△BAC全等,两边及其一边的对角分别相等的两个三角形不一定全等.
考题变式·提能力
解:因为∠ABC=∠ACB,所以AB=AC
又因为点D,E分别为边AB,AC中点所以AD=AE,AD=AF
在△ADC和△AEB中:AD=AE,∠A=∠A ,AC=AB,所以△ADC≌△AEB.所以BE=CD
【母题变式】
[变式一]解:因为AB=AC,AE=AF 所以AB-AE=AC-AF,即BE=CF
在△EBC和△FCB中:EB =CF ,∠EBC=∠FCB ,BC=BC,所以△EBC≌△FCB(SAS).
[变式二]解:在△ABE和△ACD中:AB=AC,∠A=∠A,AE=AD,所以△ABE≌△ACD,所以∠B=∠C
[变式三]解:因为点E,F分别是AB,AC的中点,所以AE=AB,AF=AC,因为AB=AC,所以AE=AF,
在△AFB和△AEC中AB=AC,∠A=∠A, AF=AE,所以△AFB≌△AEC。
新知识记:
1.判定三角形全等是方法(4)
两边及其 分别相等的两个三角形全等,(简写成“ ”或“ ”)。
2.应用格式
如图所示:
AB=DE
在△ABC与△DEF中 所以△ABC△ABC与△DEF△DEF(SAS)
AC=DF
3.全等三角形对应的中线、角平分线、高线、面积等都 。
典例精析·拓新知
知识点一 应用“SAS"证明三角形全等
【典例1】(2017·南充中考)如图,DE⊥AB,CF⊥AB,垂足分别是点E,F,DE=CF,AE=BF。试说明:AC∥BD
【规范解答】因为AE=BF 所以AE+EF=BF+EF,即AF=BE
………等量加等量和相等
因为DE⊥AB,CF⊥AB,所以∠AFC=∠BED=90°………垂直定义
在△AFC和△BED中:AF = BE,∠AFC=∠BED,CF=DE,
所以△AFC≌△BED.(SAS)
所以∠A=∠B…………全等三角形的对应角相等
所以AC∥BD.…………内错角相等,两直线平行
学霸提醒:
应用“SAS"判定两个三角形全等的“两点注意”
1.对应:“SAS”包含“边”“角”两种元素,一定要注意元素的“对应”关系。
2.顺序:在应用时一定要按边→角→边的顺序排列条件,绝不能出现边→边→角(或角→边一边)的错误,因为边边角(或角边边)不能保证两个三角形全等。
【变式训练】如图,DE⊥AB,CF⊥AB,垂足分别是 E,F,DE=CF,AE=BF.试说明:AC=BD。
知识点二 三角形全等判定方法的综合应用
【典例2】如图,在△ABC中,点D,E分别在AB,AC上,AB=AC,BD=CE,BE与CD交于点O。试说明:△BCE≌△CBD【自主解答】
学霸提醒
由已知说明两个三角形全等的一般思路
若已知两边→(找夹角→SAS);找第三边→SSS
若已知一边一角→
①边为角的对边→找任一角→AAS
②找角的另一邻边→SAS:边为角的邻边→SAS;找边的另一邻角→ASA;找边的对角→AAS;
(3)若已知两角→找夹边→ASA;找任一角的对边→AAS
【变式训练】在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.试说明:PB=PC,并直接写出图中其他相等的线段。
达标训练·夯基础
知识点一 应用“SAS"证明三角形全等
1.如图,在△ABC和△DEF中,ABDE,∠B=∠E,补充下列哪一个条件后,
能直接应用“SAS”判定△ABC≌△DEF
A.∠ACB=∠DFE B.BF=ECD C.AC=DF D.∠A=∠D
2.(2018·宿州月考)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
A.∠A=∠C B.∠D=∠B C.AD∥BC D.DF∥BE
3.如图,AD和CB相交于点E,BE=DE,请添加一个条件,能利用“SAS”判定△ABE≌△CDE(只添加一个条件即可),你所添加的条件是 。
如图,AB是∠DAC的平分线,且AD=AC.试说明:BD=BC。
5.(2017·吉林中考)如图,点E,F在BC上,BE=FC,AB=DC,∠B=∠C.试说明:∠A=∠D。
知识点二 三角形全等判定方法的综合应用
1.(2018·德州乐陵期中)下列条件中不能判定△ABC≌△DEF的是( )
A.AB=DE, AC=DF, BC=EF B.AB=DE,∠A=∠D,BC=EF
C.AB=DE,∠B=∠DEF,BC=EF D.∠B=∠DEF,∠A=∠D,AB=DE
2.(2018·诸暨市期中)如图(1),已知△ABC的六个元素,则图(2)、图(3)、图(4)中的三角形和△ABC全等的有( )
A.图(2)和图(3)
B.图(3)和图(4)
C.只有图(3)
D.只有图(4)
(2018·常德模拟)如图,点P在∠AOB的平分线上,若使△AOP0≌△BOP,
则需添加的一个条件是 (只写一个即可,不添加辅助线)
4.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2
(1)试说明:BD=CE.
(2)试说明:∠M=∠N.
纠错园
如图,AC,BD相交于点E.∠D=∠C,AD=BC,
试说明:△ABD≌△BAC
解:在△ABD和△BAC中
因为AD=BC ∠D=∠C, AB=BA
所以△ABD≌△BAC(SAS)
【错因】
考题变式·提能力
(2017·郴州中考)已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB,AC的中点.
试说明:BE=CD
母题变式
【变式一】在△ABC中,AB=AC,点E,F分别在 AB,AC上,AE=AF,∠ABC=∠ACB,
BF与CE相交于点P。
试说明:△EBC≌△FCB。
【变式二】如图,点D,E分别是AB,AC上的点,且AB=AC,AD=AE.试说明:∠B=∠C。
【变式三】如图,AB=AC,点E,F分别是AB,AC的点.试说明:△AFB≌△AEC。
参考答案及解析
新知识记
1.夹角 边角边 SAS 2.∠A=∠D 3.相等
典例精析·拓新知
【典例1】【变式训练】
解:因为AE=BF,所以AE+EF=BF+EF,即AF=BE
因为DE⊥AB,CF⊥AB,所以∠AFC=∠BED=90o
在△AFC和△BED中 :AF=BE,∠AFC=∠BED,CF=DE,所以AFC≌△BED(SAS).所以AC=DE。
【典例2】【自主解答】因为AB=AC,BD=CE,所以AB-BD=AC-CE,即AD=AB=AC,∠BAE=∠CAD,AE=AD,
所以△ABE≌△ACD(SAS),所以DC=BE,在△DBC与△ECB中,DB=EC,DC=EB. BC=CB,
所以△BCE≌△CBD(SSS)
【变式训练】解:在△ABF和△ACE中:AB=AC,∠BAF=∠CAE,AF=AE, 所以△ABF≌△ACE(SAS)
所以∠ABF=∠ACE(全等三角形的对应角相等) BF=CE(全等三角形的对应边相等)
因为AB=AC,AE=AF,所以BE=CF,在△BEP和△CFP中: ∠BPE=∠CPF,∠PBE=∠PCF,BE =CF
所以△BEP≌△CFP(AAS),所以PB=PC,因为BF=CE所以PE=PF,所以图中相等的线段为PE=PF,BF=CE。
达标训练·夯基础
1.B 2.B 3. AE=CE
4.解:因为AB是∠DAC的平分线,所以∠DAB=∠BAC,在△DAB和△CAB中,AD=AC,∠DAB=∠CAB,AB=AB,所以△DAB≌△CAB(SAS),所以BD=BC
5.解:因为BE=FC,所以BE+EF=CF+EF;又因为AB=DC,∠B=∠C,所以△ABF≌△DCE(SAS),
所以∠A=∠D。
知识点二
1.B 2.D
3.OA=OB(或∠OAP=∠OBP或∠OPA=∠OPB.答案不唯一)
4.解:(1)在△ABD和△ACE中,AB=AC,∠1=∠2,AD=AE,所以△ABD≌△ACE(SAS)所以BD=CE。
(2)因为∠1=∠2,所以∠1+∠DAE=∠2+∠DAE即∠BAN=∠CAM
由(1)得△ABD≌△ACE,所以∠B=∠C,在△ACM和△ABN中:∠C=∠B,AC=AB,∠CAM=∠BAN,
所以△ACM≌△ABN(ASA)所以∠M=∠N
【纠错园】
根据条件不能直接利用SAS判定△ABD和△BAC全等,两边及其一边的对角分别相等的两个三角形不一定全等.
考题变式·提能力
解:因为∠ABC=∠ACB,所以AB=AC
又因为点D,E分别为边AB,AC中点所以AD=AE,AD=AF
在△ADC和△AEB中:AD=AE,∠A=∠A ,AC=AB,所以△ADC≌△AEB.所以BE=CD
【母题变式】
[变式一]解:因为AB=AC,AE=AF 所以AB-AE=AC-AF,即BE=CF
在△EBC和△FCB中:EB =CF ,∠EBC=∠FCB ,BC=BC,所以△EBC≌△FCB(SAS).
[变式二]解:在△ABE和△ACD中:AB=AC,∠A=∠A,AE=AD,所以△ABE≌△ACD,所以∠B=∠C
[变式三]解:因为点E,F分别是AB,AC的中点,所以AE=AB,AF=AC,因为AB=AC,所以AE=AF,
在△AFB和△AEC中AB=AC,∠A=∠A, AF=AE,所以△AFB≌△AEC。
