2018高中物理专题3.5力的分解同步课件新人教版必修1:52张PPT
文档属性
| 名称 | 2018高中物理专题3.5力的分解同步课件新人教版必修1:52张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-09-17 09:08:42 | ||
图片预览




文档简介
课件52张PPT。第三章 相互作用学习目标1、理解分力及力的分解的概念
2、理解力的分解与力的合成互为逆运算,且都遵守力的平行四边形定则
3、掌握按力的作用效果进行分解的一般步骤,学会判断一个力产生的实际效果
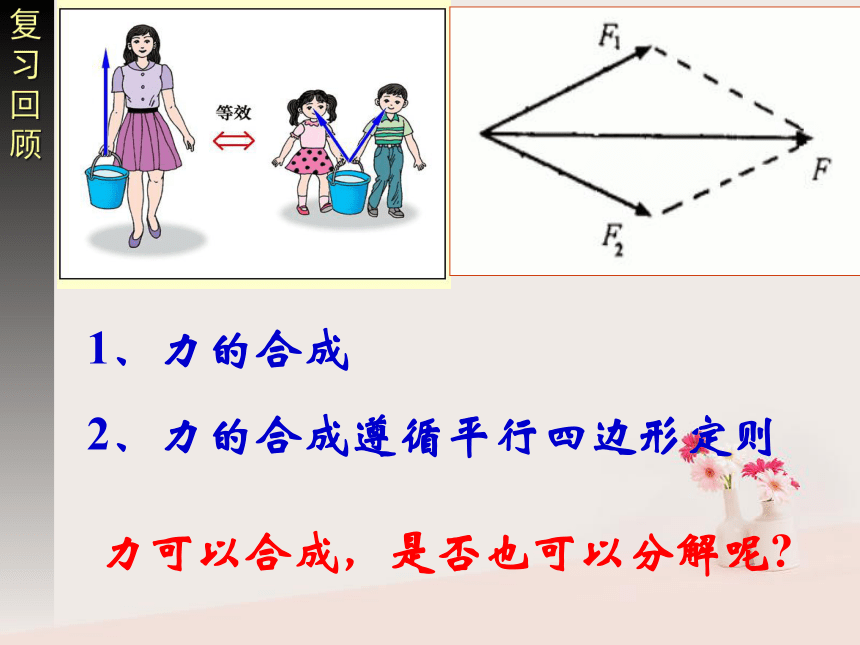
4、知道合力和(两等大)分力之间的大小关系 1、力的合成
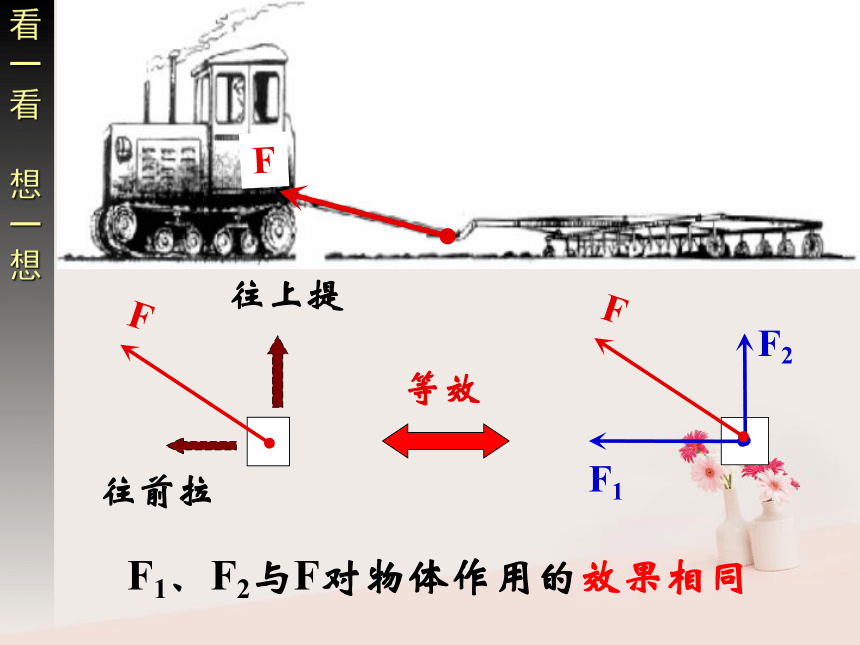
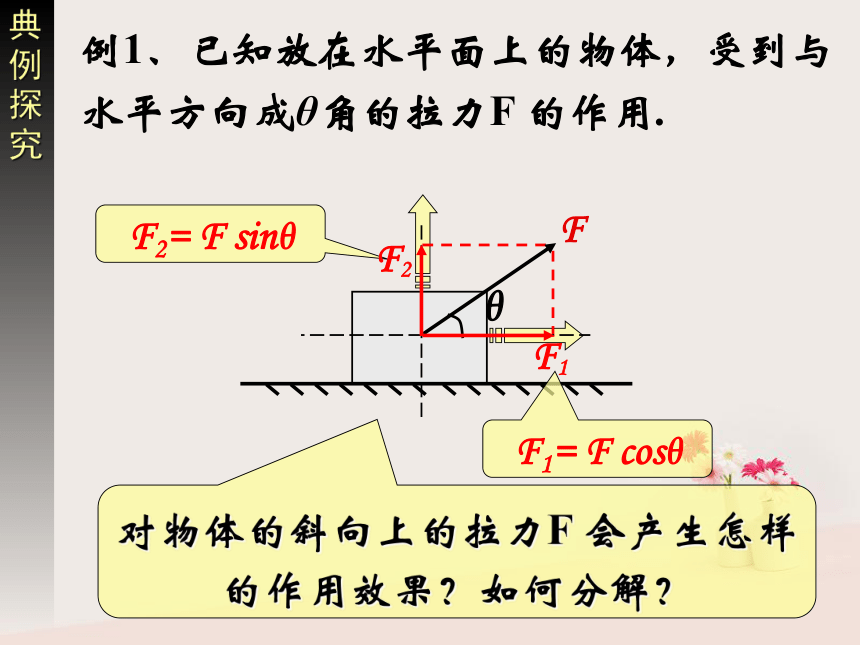
2、力的合成遵循平行四边形定则复习回顾力可以合成,是否也可以分解呢?看一看 想一想F1、F2与F对物体作用的效果相同1、力的分解:
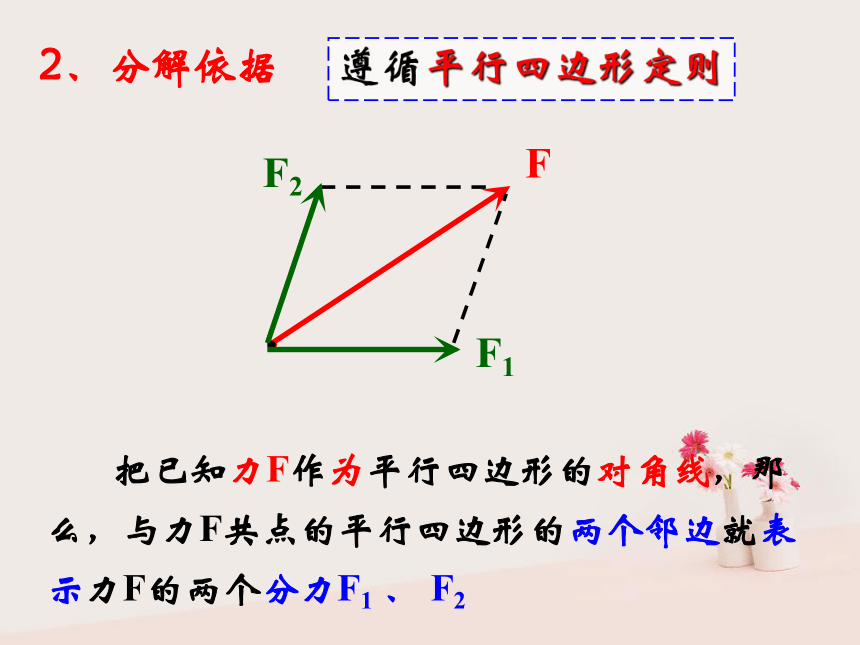
已知一个力求它的分力的过程.一、力的分解注意:①力的分解是力的合成的逆运算;
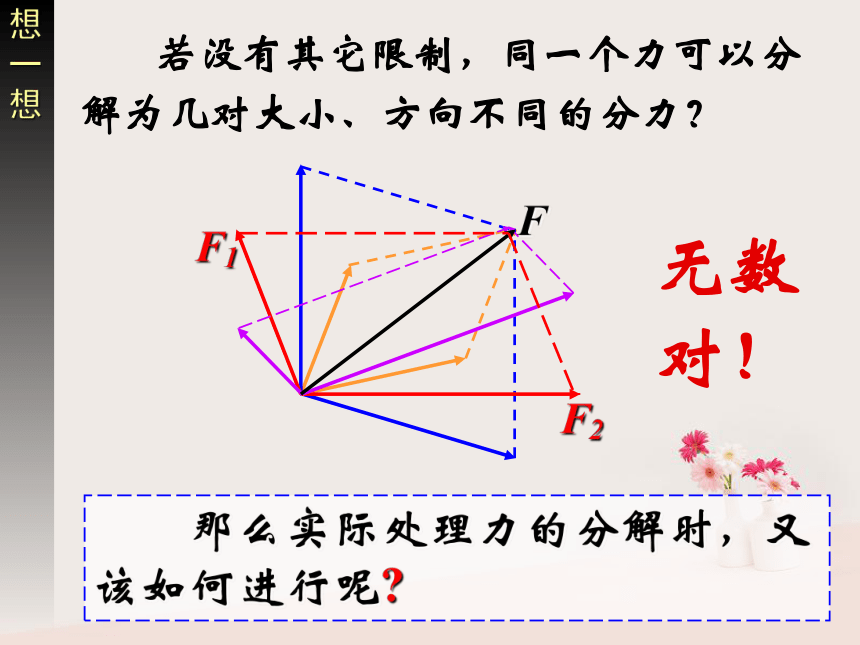
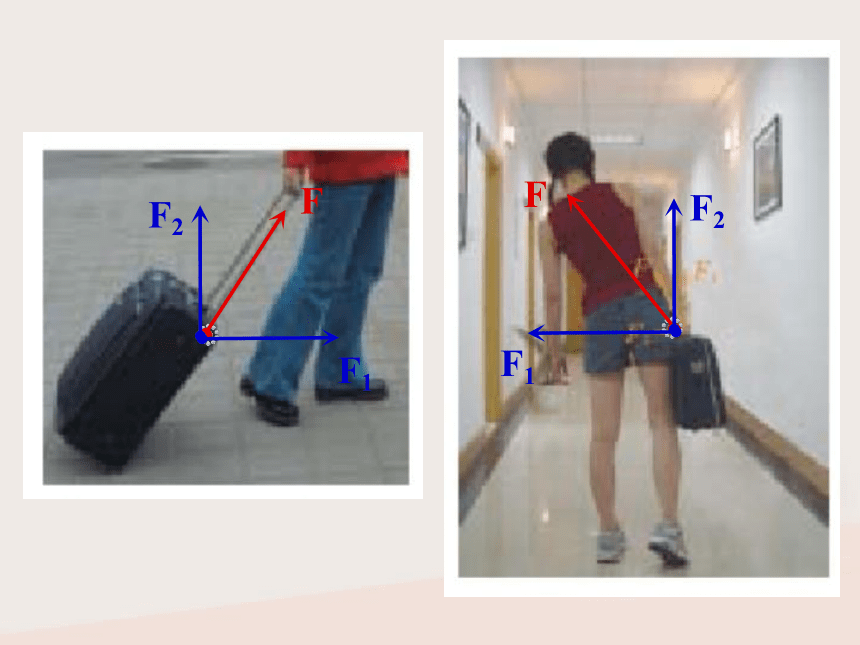
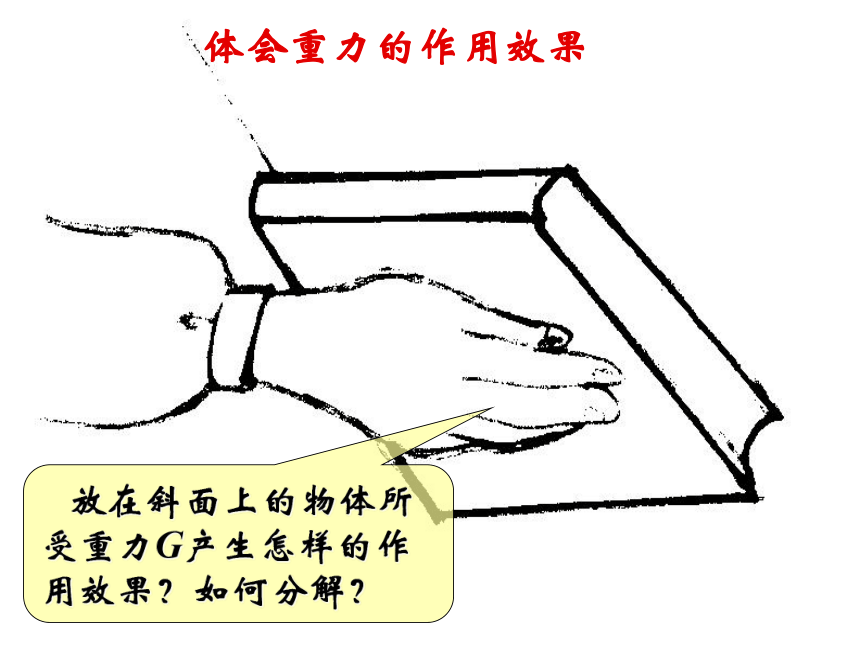
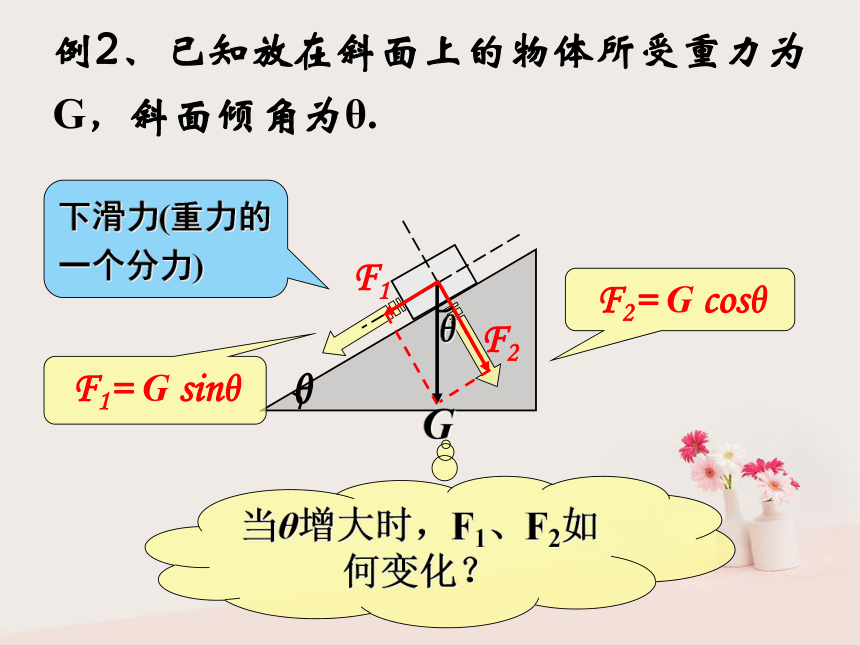
②几个分力与原来那个力是等效的,它们可以互相代替,并非同时并存!!!2、分解依据 把已知力F作为平行四边形的对角线,那么,与力F共点的平行四边形的两个邻边就表示力F的两个分力F1 、 F2遵循平行四边形定则想一想 若没有其它限制,同一个力可以分解为几对大小、方向不同的分力?无数对! 那么实际处理力的分解时,又该如何进行呢?F2= F sinθF1= F cosθ典例探究例1、已知放在水平面上的物体,受到与水平方向成θ角的拉力F 的作用.对物体的斜向上的拉力F 会产生怎样的作用效果?如何分解? 放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?例2、已知放在斜面上的物体所受重力为G,斜面倾角为θ.F1= G sinθ下滑力(重力的一个分力)F2= G cosθ当θ增大时,F1、F2如何变化?实例分析力分解的步骤4、据三角形知识求分力的大小和方向.3、用平行四边形定则定分力的大小;
(把力F作为对角线,画平行四边形得分力)1、分析力的作用效果;2、据力的作用效果定分力的方向;
(画两个分力的方向)例3、已知放在斜面上的物体所受重力为G,斜面倾角为θ.F2= G cosθF1= G sinθF1= G tanθF2= G/cosθ拉力F怎么分解?F1= F /tanθF2= F /sinθ动手感受一下F1= F /sinθF2= F /tanθ例4、可自由转动的轻杆AC 和BC ,BC 杆水平,在它们的连接处C点施加一个竖直向下的力F .F1= G cosθF2= G sinθ例5、用两根轻绳将物体悬挂起来。已知物体重力为G,轻绳AO与水平方向夹角为θ,AOB为直角. 合力一定,两等大分力随它们之间的夹角变化而如何变化?分力随夹角增大而增大交流与讨论 人字型支架,夹角较大时,用指力就可以很轻松的将铁丝拉断,为什么会这样?◇四两可以拨千斤体验分力的大小与合力的大小的关系.生活应用赵州桥是当今世界上跨径最大、建造最早的单孔敞肩型石拱桥,距今1400多年. 分析我们取石拱桥上面的石块A进行分析,就会发现拱桥上面物体的重力压在A上对A施加向下压力.由于A是楔形不能向下移动,只能挤压相邻的B、C. 已知合力和两个分力的方向(F1、F2不在同一直线上)
已知合力和两个分力的大小(F1+F2> F且F1≠F2)
已知合力和一个分力的大小与方向
F2F1一组解一组解两组解三、力的分解确定解情况3.当F sinθ2.当F1 < Fsinθ 时
4.当F1 ≥F 时
已知合力和一个分力的方向和另一个分力的大小1.当F1 = Fsinθ 时
一组解无解两组解一组解 把力沿两个互相垂直的方向进行分解的方法叫做力的正交分解法.Fx =F1x+F2x+F3x+…Fy =F1y+F2y+F3y+…F3x = F3
F3y = 0坐标的选取:原则上是任意的,但实际问题中,让尽可能多的力落在这个方向上,这样就可以尽可能少分解力.附:力的正交分解例1、质量为m的木块在推力F作用下,在水平地面上做匀速运动.已知木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力为下列各值的哪个( )
A.μmg
B.μ(mg+F sinθ)
C.μ(mg+F sinθ)
D.F cosθB、D例2、 如图,物体A的质量为m,斜面倾角α,A与斜面间的动摩擦因数为μ,斜面固定,现有一个水平力F作用在A上,当F多大时,物体A恰能沿斜面匀速向上运动?例3、如图所示,物体受到F1、F2和F3的作用, F2与F3的夹角为1350 ,F1与F3的夹角为1500,其中F3=10N,物体处于静止状态,则F1和F2的大小各为多少?xyoF1F2F3F1XF1yF2XF2y例4 、木箱重500 N,放在水平地面上,一个人用大小为200 N与水平方向成30°向上的力拉木箱,木箱沿地平面匀速运动,求木箱受到的摩擦力和地面所受的压力。二、矢量相加的法则【探求】人从A到B,再到C的过程中,总位移与两段位移的关系?另一分矢量分矢量合矢量把两个矢量首尾相接从而求出合矢量的方法叫做三角形定则三角形定则与平行四边形定则实质一样矢量:在物理学中,像力一样即有大小,又有方向的物理量叫做矢量.
矢量在相加时遵守平行四边形定则(或三角形定则).
如:力、速度、位移等.标量:在物理学中,只有大小、没有方向的物理量叫做标量.
标量在计算时遵循算术运算法则.
如:时间、质量、长度等. 如图,一个物体的速度v1 在一小段时间内发生了变化,变成了v2 。你能根据v1 、v2 ,按照三角形定则找出变化量Δv 吗?
说一说课堂小结一、力的分解遵守平行四边形定则1、定 解 条 件(1)已知两分力的方向(2)已知一个分力的大小和方向2、效果分解法(1) 据力的作用效果定分力的方向(2) 用平行四边形定则定分力的大小(3)据三角形知识求分力的大小和方向3、正交分解法:沿两互相垂直的方向分解课堂小结二、矢量(加、减)运算法则2、矢量:有大小,又有方向,相加时遵守平行四边形定则 (或三角形定则)1、法则:平行四边形定则 (或三角形定则) 将一个力F分解成两个分力F1、F2,而分力F1、F2都是矢量,有大小、方向;那么两个大小、方向如何去构造平行四边形呢?能有几种情形呢?
以代表的合力的有向线段为对角线,代表两分力的有向线段为邻边,如果可以构成平行四边形(三角形),说明合力可以分解成给定的力,即有解;如果不能构成平行四边形(三角形),说明该合力不能按成给定的分力分解,即无解想一想1.正交分解法
定义:把力按作用效果沿两个相互垂直的坐标轴分解的方法叫正交分解法. 可将力F分解成Fx和Fy,且它们的关系是: Fx=Fcosα Fy=Fsinα
※坐标轴选取的原则 在求解多个力的合力时,运用正交分解法比较简单,要尽量减少分解未知的力,即将可能多的力建立在坐标轴上,使求解问题简化.
※正交分解的实质 将矢量运算转化为代数运算.在求解力学综合题时经常用到的解题方法2.动态分析法 利用平行四边形定则或三角形定则将物体的受力情况作一个基础分析,利用题中给出的信息(某个角度的变化或某个力大小的变化)从图中观察其它力的变化的方法.
例:如图,挡板AB和竖直墙之间夹有小球,球的质量为m,则当挡板与竖直墙壁之间夹角ɑ缓缓增加时,AB板及墙对球的压力如何变化?练习1、如图,重G的光滑小球静止在固定斜面和竖直挡板之间。若挡板逆时针缓慢转到水平位置,在该过程中,斜面和挡板对小球的弹力的大小F1、F2变化情况是( )
A. F1增大
B. F2先减小后增大
C. F2增大
D. F2减少B解析:以球为研究对象,球所受重力mg产生的效果有两个:对挡板产生的压力FN2,其大小等于F2;对斜面产生的压力FN2,其大小等于F1.
根据重力产生的效果将重力分解,如图所示,当挡板与斜面夹角为β,由图示位置变化时,F1的大小改变,但方向不变(与竖直方向成α角),始终垂直斜面;F2的方向总是垂直于挡板AO,其大小、方向均变化,由图可知,当β=90°时,挡板AO所受压力大小F2最小,最小值为mgsin α.练习2:用两根轻绳将一水桶悬挂起来,已知轻绳BO与水平方向夹角为53 °,∠AOB为90 °.
两根轻绳能承受的最大拉力相同,当往水桶里不断加水时,哪根绳子会先断?
OA水平3.相似三角形法 利用题中所给出的图形当中的几何三角形与分析问题所得到的矢量三角形相似进行解题.
例:图中为一悬挂重物的三角形支架示意图,三角形三边长度之比为LAB:LAC:LBC=2:3:4,当支架顶端悬挂的重物为G时,BC杆和AC绳受到的力分别为多少? 练习1:如图,光滑圆柱体半径为R,在圆心O的正上方力顶点高h处有一定滑轮,通过定滑轮用细绳拉一质量为m的小球由A点(OA水平)沿圆柱缓慢运动到B点。求:
(1)此过程中,该球对圆柱体的压力.
(2)分析此过程中,绳对球的拉力F如何变化.练习2: 如图,支杆BC一端用铰链固定于B,另一端连接滑轮C,重物P上系一轻绳经C固定于墙上A点. 若杆BC、滑轮C及绳子的质量、摩擦均不计,将绳端A点沿墙稍向下移,再使之平衡时,绳的拉力和BC杆受到的压力如何变化?1.对一个已知力进行分解的几种常见的情况平行四边形定则三角形定则或提示:一般情况下,矢量可以平移*三角形定则实例(三)不同位置分解重力G一小球从一大球顶上滚下
2、理解力的分解与力的合成互为逆运算,且都遵守力的平行四边形定则
3、掌握按力的作用效果进行分解的一般步骤,学会判断一个力产生的实际效果
4、知道合力和(两等大)分力之间的大小关系 1、力的合成
2、力的合成遵循平行四边形定则复习回顾力可以合成,是否也可以分解呢?看一看 想一想F1、F2与F对物体作用的效果相同1、力的分解:
已知一个力求它的分力的过程.一、力的分解注意:①力的分解是力的合成的逆运算;
②几个分力与原来那个力是等效的,它们可以互相代替,并非同时并存!!!2、分解依据 把已知力F作为平行四边形的对角线,那么,与力F共点的平行四边形的两个邻边就表示力F的两个分力F1 、 F2遵循平行四边形定则想一想 若没有其它限制,同一个力可以分解为几对大小、方向不同的分力?无数对! 那么实际处理力的分解时,又该如何进行呢?F2= F sinθF1= F cosθ典例探究例1、已知放在水平面上的物体,受到与水平方向成θ角的拉力F 的作用.对物体的斜向上的拉力F 会产生怎样的作用效果?如何分解? 放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?例2、已知放在斜面上的物体所受重力为G,斜面倾角为θ.F1= G sinθ下滑力(重力的一个分力)F2= G cosθ当θ增大时,F1、F2如何变化?实例分析力分解的步骤4、据三角形知识求分力的大小和方向.3、用平行四边形定则定分力的大小;
(把力F作为对角线,画平行四边形得分力)1、分析力的作用效果;2、据力的作用效果定分力的方向;
(画两个分力的方向)例3、已知放在斜面上的物体所受重力为G,斜面倾角为θ.F2= G cosθF1= G sinθF1= G tanθF2= G/cosθ拉力F怎么分解?F1= F /tanθF2= F /sinθ动手感受一下F1= F /sinθF2= F /tanθ例4、可自由转动的轻杆AC 和BC ,BC 杆水平,在它们的连接处C点施加一个竖直向下的力F .F1= G cosθF2= G sinθ例5、用两根轻绳将物体悬挂起来。已知物体重力为G,轻绳AO与水平方向夹角为θ,AOB为直角. 合力一定,两等大分力随它们之间的夹角变化而如何变化?分力随夹角增大而增大交流与讨论 人字型支架,夹角较大时,用指力就可以很轻松的将铁丝拉断,为什么会这样?◇四两可以拨千斤体验分力的大小与合力的大小的关系.生活应用赵州桥是当今世界上跨径最大、建造最早的单孔敞肩型石拱桥,距今1400多年. 分析我们取石拱桥上面的石块A进行分析,就会发现拱桥上面物体的重力压在A上对A施加向下压力.由于A是楔形不能向下移动,只能挤压相邻的B、C. 已知合力和两个分力的方向(F1、F2不在同一直线上)
已知合力和两个分力的大小(F1+F2> F且F1≠F2)
已知合力和一个分力的大小与方向
F2F1一组解一组解两组解三、力的分解确定解情况3.当F sinθ
4.当F1 ≥F 时
已知合力和一个分力的方向和另一个分力的大小1.当F1 = Fsinθ 时
一组解无解两组解一组解 把力沿两个互相垂直的方向进行分解的方法叫做力的正交分解法.Fx =F1x+F2x+F3x+…Fy =F1y+F2y+F3y+…F3x = F3
F3y = 0坐标的选取:原则上是任意的,但实际问题中,让尽可能多的力落在这个方向上,这样就可以尽可能少分解力.附:力的正交分解例1、质量为m的木块在推力F作用下,在水平地面上做匀速运动.已知木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力为下列各值的哪个( )
A.μmg
B.μ(mg+F sinθ)
C.μ(mg+F sinθ)
D.F cosθB、D例2、 如图,物体A的质量为m,斜面倾角α,A与斜面间的动摩擦因数为μ,斜面固定,现有一个水平力F作用在A上,当F多大时,物体A恰能沿斜面匀速向上运动?例3、如图所示,物体受到F1、F2和F3的作用, F2与F3的夹角为1350 ,F1与F3的夹角为1500,其中F3=10N,物体处于静止状态,则F1和F2的大小各为多少?xyoF1F2F3F1XF1yF2XF2y例4 、木箱重500 N,放在水平地面上,一个人用大小为200 N与水平方向成30°向上的力拉木箱,木箱沿地平面匀速运动,求木箱受到的摩擦力和地面所受的压力。二、矢量相加的法则【探求】人从A到B,再到C的过程中,总位移与两段位移的关系?另一分矢量分矢量合矢量把两个矢量首尾相接从而求出合矢量的方法叫做三角形定则三角形定则与平行四边形定则实质一样矢量:在物理学中,像力一样即有大小,又有方向的物理量叫做矢量.
矢量在相加时遵守平行四边形定则(或三角形定则).
如:力、速度、位移等.标量:在物理学中,只有大小、没有方向的物理量叫做标量.
标量在计算时遵循算术运算法则.
如:时间、质量、长度等. 如图,一个物体的速度v1 在一小段时间内发生了变化,变成了v2 。你能根据v1 、v2 ,按照三角形定则找出变化量Δv 吗?
说一说课堂小结一、力的分解遵守平行四边形定则1、定 解 条 件(1)已知两分力的方向(2)已知一个分力的大小和方向2、效果分解法(1) 据力的作用效果定分力的方向(2) 用平行四边形定则定分力的大小(3)据三角形知识求分力的大小和方向3、正交分解法:沿两互相垂直的方向分解课堂小结二、矢量(加、减)运算法则2、矢量:有大小,又有方向,相加时遵守平行四边形定则 (或三角形定则)1、法则:平行四边形定则 (或三角形定则) 将一个力F分解成两个分力F1、F2,而分力F1、F2都是矢量,有大小、方向;那么两个大小、方向如何去构造平行四边形呢?能有几种情形呢?
以代表的合力的有向线段为对角线,代表两分力的有向线段为邻边,如果可以构成平行四边形(三角形),说明合力可以分解成给定的力,即有解;如果不能构成平行四边形(三角形),说明该合力不能按成给定的分力分解,即无解想一想1.正交分解法
定义:把力按作用效果沿两个相互垂直的坐标轴分解的方法叫正交分解法. 可将力F分解成Fx和Fy,且它们的关系是: Fx=Fcosα Fy=Fsinα
※坐标轴选取的原则 在求解多个力的合力时,运用正交分解法比较简单,要尽量减少分解未知的力,即将可能多的力建立在坐标轴上,使求解问题简化.
※正交分解的实质 将矢量运算转化为代数运算.在求解力学综合题时经常用到的解题方法2.动态分析法 利用平行四边形定则或三角形定则将物体的受力情况作一个基础分析,利用题中给出的信息(某个角度的变化或某个力大小的变化)从图中观察其它力的变化的方法.
例:如图,挡板AB和竖直墙之间夹有小球,球的质量为m,则当挡板与竖直墙壁之间夹角ɑ缓缓增加时,AB板及墙对球的压力如何变化?练习1、如图,重G的光滑小球静止在固定斜面和竖直挡板之间。若挡板逆时针缓慢转到水平位置,在该过程中,斜面和挡板对小球的弹力的大小F1、F2变化情况是( )
A. F1增大
B. F2先减小后增大
C. F2增大
D. F2减少B解析:以球为研究对象,球所受重力mg产生的效果有两个:对挡板产生的压力FN2,其大小等于F2;对斜面产生的压力FN2,其大小等于F1.
根据重力产生的效果将重力分解,如图所示,当挡板与斜面夹角为β,由图示位置变化时,F1的大小改变,但方向不变(与竖直方向成α角),始终垂直斜面;F2的方向总是垂直于挡板AO,其大小、方向均变化,由图可知,当β=90°时,挡板AO所受压力大小F2最小,最小值为mgsin α.练习2:用两根轻绳将一水桶悬挂起来,已知轻绳BO与水平方向夹角为53 °,∠AOB为90 °.
两根轻绳能承受的最大拉力相同,当往水桶里不断加水时,哪根绳子会先断?
OA水平3.相似三角形法 利用题中所给出的图形当中的几何三角形与分析问题所得到的矢量三角形相似进行解题.
例:图中为一悬挂重物的三角形支架示意图,三角形三边长度之比为LAB:LAC:LBC=2:3:4,当支架顶端悬挂的重物为G时,BC杆和AC绳受到的力分别为多少? 练习1:如图,光滑圆柱体半径为R,在圆心O的正上方力顶点高h处有一定滑轮,通过定滑轮用细绳拉一质量为m的小球由A点(OA水平)沿圆柱缓慢运动到B点。求:
(1)此过程中,该球对圆柱体的压力.
(2)分析此过程中,绳对球的拉力F如何变化.练习2: 如图,支杆BC一端用铰链固定于B,另一端连接滑轮C,重物P上系一轻绳经C固定于墙上A点. 若杆BC、滑轮C及绳子的质量、摩擦均不计,将绳端A点沿墙稍向下移,再使之平衡时,绳的拉力和BC杆受到的压力如何变化?1.对一个已知力进行分解的几种常见的情况平行四边形定则三角形定则或提示:一般情况下,矢量可以平移*三角形定则实例(三)不同位置分解重力G一小球从一大球顶上滚下
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
