【走进重高汇编】八上数学第十一章 多边形及其内角和测试卷(第3节)
文档属性
| 名称 | 【走进重高汇编】八上数学第十一章 多边形及其内角和测试卷(第3节) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-17 00:00:00 | ||
图片预览


文档简介
【走进重高汇编】八上数学第十一章 多边形及其内角和(第3节)
一.选择题(共10小题)
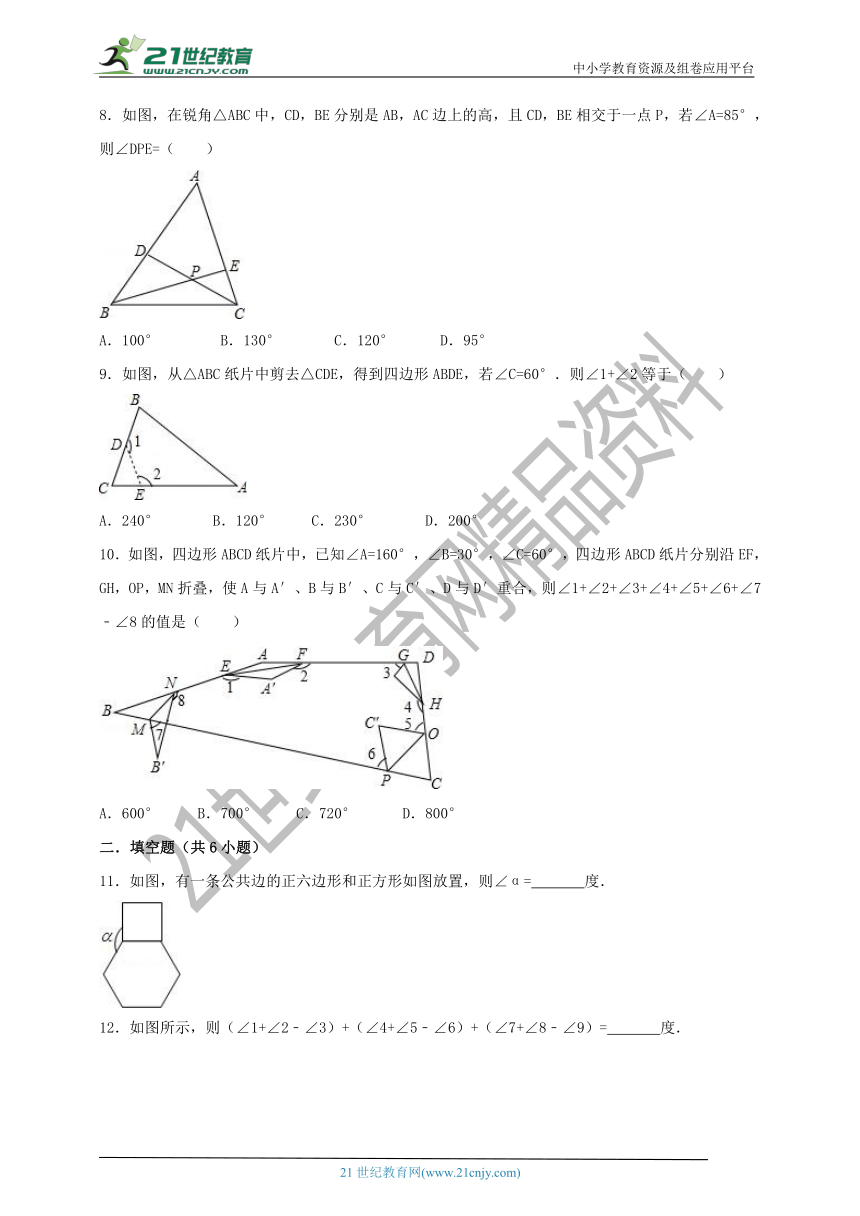
1.如果一个正多边形的一个内角是140°,那么这个正多边形的边数是( )
A.10 B.9 C.8 D.7
2.当多边形边数增加一条时,多边形的内、外角和的变化情况是( )
A.内角和、外角和都不变 B.内角和、外角和各增加180°
C.内角和不变,外角和增加180° D.内角和增加180°,外角和不变
3.一个多边形的内角都相等,它的每一个外角都等于45度,则该多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
4.如图1是四边形纸片ABCD,其中∠B=120°,∠D=50°.如果将其右下角向内折出△PCR,如图2所示,恰使CP∥AB,RC∥AD,则∠C的度数为( )
A.105° B.100° C.95° D.90°
5.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
6.如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
A.40° B.45° C.50° D.60°
7.如图,小明将几块六边形纸片分别减掉了一部分(虚线部分),得到了一个新多边形.若新多边形的内角和为540°,则对应的是下列哪个图形( )
A. B. C. D.
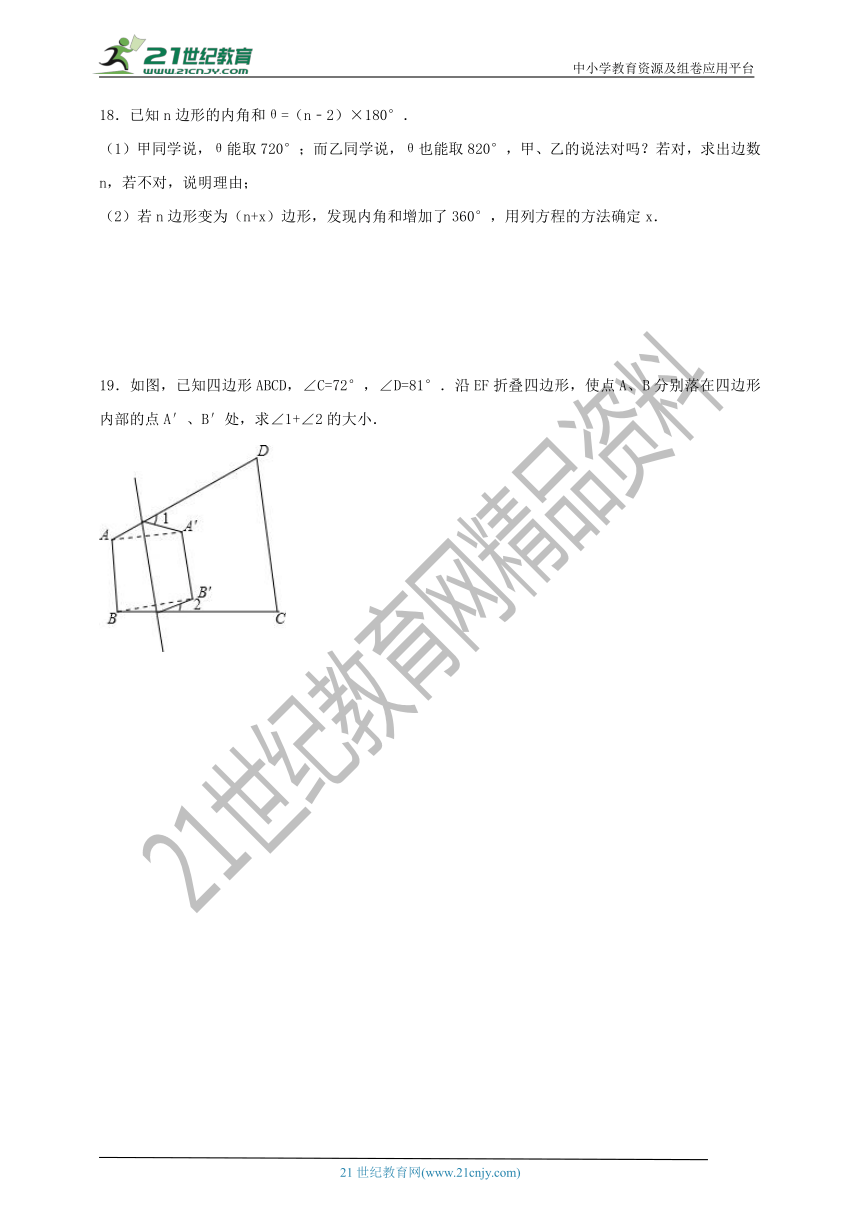
8.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=85°,则∠DPE=( )
A.100° B.130° C.120° D.95°
9.如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )
A.240° B.120° C.230° D.200°
10.如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )
A.600° B.700° C.720° D.800°
二.填空题(共6小题)
11.如图,有一条公共边的正六边形和正方形如图放置,则∠α= 度.
12.如图所示,则(∠1+∠2﹣∠3)+(∠4+∠5﹣∠6)+(∠7+∠8﹣∠9)= 度.
13.如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…这样他以3m/s的速度匀速的一直走下去,他第一次回到出发点A时,一共走了 s.
14.已知如图,∠3+∠5+∠7=200°,则∠1+∠2+∠4+∠6+∠8= .
15.如果一个多边形的所有内角从小到大排列起来,恰好依次增加相同的度数,设最小角的度数为100°,最大角的度数为140°,那么这个多边形是 边形.
16.在如图一、图二、图三中,分别是由1个、2个、n个正方形连接成的图形.在图1中,x=70°;在图二中,y=28°;通过(1)、(2)的计算,请写出图三中a+b+c+…+d与n的数量关系式 .
三.解答题(共7小题)
17.小明在计算一个多边形的内角和,求得的内角和为2220°,经过检查发现少加了一个内角,请问这个内角为多少度?这个多边形是几边形?
18.已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取720°;而乙同学说,θ也能取820°,甲、乙的说法对吗?若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
19.如图,已知四边形ABCD,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,求∠1+∠2的大小.
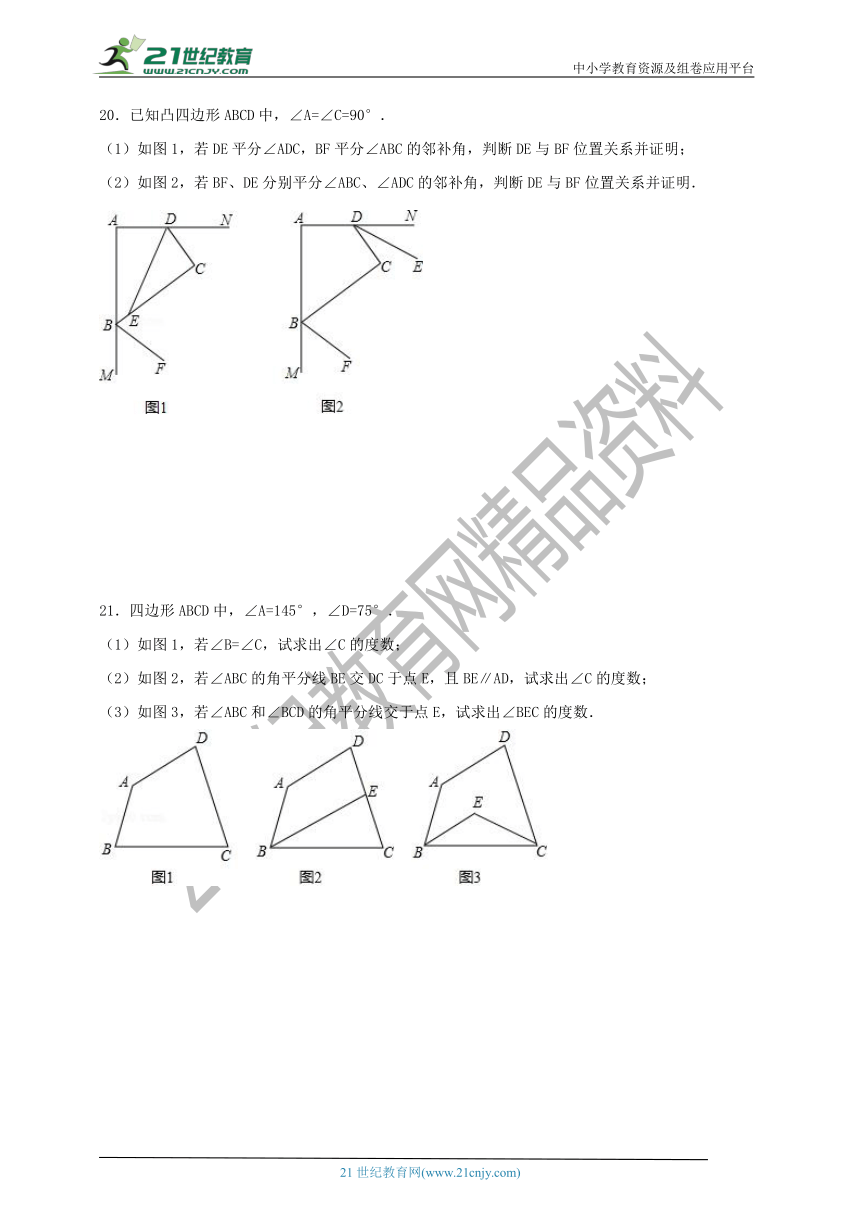
20.已知凸四边形ABCD中,∠A=∠C=90°.
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明;
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
21.四边形ABCD中,∠A=145°,∠D=75°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
22.如图,△ADE和△ABC中∠EAD=∠AED=∠BAC=∠BCA=45°,又有∠BAD=∠BCF.
(1)求∠ECF+DAC+∠ECA的度数;
(2)判断ED与FC的位置关系,并对你的结论加以证明.
23.已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=100°,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,则∠ABD+∠ACD= 度
(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由;
(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论 .(填“能”或“不能”)
【走进重高汇编】八上数学第十一章 多边形及其内角和(第3节)
参考答案与试题解析
一.选择题(共10小题)
1.如果一个正多边形的一个内角是140°,那么这个正多边形的边数是( )
A.10 B.9 C.8 D.7
【分析】根据多边形的内角和公式(n﹣2)?180°列式进行计算即可得解.
【解答】解:设这个正多边形的边数是n,
根据题意得,(n﹣2)?180°=140°?n,
解得n=9.故选:B.
2.当多边形边数增加一条时,多边形的内、外角和的变化情况是( )
A.内角和、外角和都不变 B.内角和、外角和各增加180°
C.内角和不变,外角和增加180° D.内角和增加180°,外角和不变
【分析】根据多边形的内角和定理以及外角和等于360°,计算后直接选择答案.
【解答】解:∵多边形内角和为(n﹣2)?180°,外角和为360°,
∴多边形边数增加一条,内角和增加180°,外角和不变.
故选:D.
3.一个多边形的内角都相等,它的每一个外角都等于45度,则该多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
【分析】先利用360°÷45°求出多边形的边数即可求解.
【解答】解:多边形的边数为:360°÷45°=8,
故选:C.
4.如图1是四边形纸片ABCD,其中∠B=120°,∠D=50°.如果将其右下角向内折出△PCR,如图2所示,恰使CP∥AB,RC∥AD,则∠C的度数为( )
A.105° B.100° C.95° D.90°
【分析】根据平行线的性质得∠BPC=180°﹣∠B=60°,∠DRC=130°,再利用三角形的内角和求出∠C的度数.
【解答】解:∵CP∥AB,RC∥AD
∴∠BPC=180°﹣∠B=60°,∠DRC=130°
∴∠C=180°﹣60°﹣25°=95°.
故选:C.
5.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
【分析】首先求得内角和为1080°的多边形的边数,即可确定原多边形的边数.
【解答】解:设内角和为1080°的多边形的边数是n,则(n﹣2)?180°=1080°,
解得:n=8.
则原多边形的边数为7或8或9.
故选:D.
6.如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
A.40° B.45° C.50° D.60°
【分析】在DO延长线上找一点M,根据多边形的外角和为360°可得出∠BOM=140°,再根据邻补角互补即可得出结论.
【解答】解:在DO延长线上找一点M,如图所示.
∵多边形的外角和为360°,
∴∠BOM=360°﹣220°=140°.
∵∠BOD+∠BOM=180°,
∴∠BOD=180°﹣∠BOM=180°﹣140°=40°.
故选:A.
【点评】本题考查了多边形的内角与外角以及邻补角,解题的关键是根据多边形的外角和为360°找出∠BOM=140°.
7.如图,小明将几块六边形纸片分别减掉了一部分(虚线部分),得到了一个新多边形.若新多边形的内角和为540°,则对应的是下列哪个图形( )
A. B. C. D.
【分析】根据新多边形的内角和为540°,n边形的内角和公式为(n﹣2)?180°,由此列方程求n.
【解答】解:设这个新多边形的边数是n,
则(n﹣2)?180°=540°,
解得:n=5,
故选:C.
【点评】本题考查了多边形外角与内角.此题比较简单,只要结合多边形的内角和公式来寻求等量关系,构建方程即可求解.
8.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=85°,则∠DPE=( )
A.100° B.130° C.120° D.95°
【分析】根据三角形的高的定义可得∠ADC=∠AEB=90°,再根据四边形内角和为360°可得∠DPE=360°﹣90°﹣90°﹣85°=95°.
【解答】解:∵CD,BE分别是AB,AC边上的高,
∴∠ADC=∠AEB=90°,
∵∠A=85°,
∴∠DPE=360°﹣90°﹣90°﹣85°=95°,
故选:D.
【点评】此题主要考查了多边形的内角,以及三角形的高,关键是掌握四边形内角和为360°.
9.如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )
A.240° B.120° C.230° D.200°
【分析】根据题意可得出∠B+∠A,再根据四边形的内角和定理可求出∠1+∠2.
【解答】解:∵∠C=60°,
∴∠B+∠A=120°,
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=240°,
故选:A.
【点评】本题考查了三角形的内角和定理,四边形的内角和定理,三角形的内角和等于180°,解决本题的关键是求出∠B+∠A.
10.如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )
A.600° B.700° C.720° D.800°
【分析】先根据四边形内角和等于360°得出∠D的度数,根据三角形内角和定理和折叠的性质可以分别得到∠1+∠2,∠3+∠4,∠5+∠6的度数,根据三角形外角的性质和折叠的性质可以得到∠7﹣∠8的度数,再相加即可求解.
【解答】解:∵四边形ABCD中,∠A=160°,∠B=30°,∠C=60°,
∴∠D=360°﹣160°﹣30°﹣60°=110°,
∴∠1+∠2=360°﹣(180°﹣160°)×2=320°,
∠3+∠4=360°﹣(180°﹣110°)×2=220°,
∠5+∠6=360°﹣(180°﹣60°)×2=120°,
∠7﹣∠8=﹣(∠B+∠B′)=﹣60°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8
=320°+220°+120°﹣60°
=600°.
故选:A.
【点评】考查了四边形内角和等于360°,三角形内角和定理,折叠的性质,以及三角形外角的性质的综合应用.
二.填空题(共6小题)
11.如图,有一条公共边的正六边形和正方形如图放置,则∠α= 150 度.
【分析】求出正六边形和正方形的内角的度数,这两个角的度数与∠α的和是360°,即可求得.
【解答】解:正六边形的内角是:(6﹣2)?180÷6=120°;
正方形的角是90度.
则∠α=360﹣120﹣90=150°.
故答案为:150°.
【点评】本题主要考查了正多边形的内角和定理,n边形的内角和是(n﹣2)?180°.
12.如图所示,则(∠1+∠2﹣∠3)+(∠4+∠5﹣∠6)+(∠7+∠8﹣∠9)= 180 度.
【分析】利用多边形的内角和公式即可求出答案.
【解答】解:∵∠1+∠2+(360°﹣∠3)+∠4+∠5+(360°﹣∠6)+∠7+∠8+(360°﹣∠9)=180°?(9﹣2)=1260度,
∴(∠1+∠2﹣∠3)+(∠4+∠5﹣∠6)+(∠7+∠8﹣∠9)=1260﹣360×3=180°.
【点评】主要考查了多边形的内角和定理.n边形的内角和为:180°(n﹣2).此类题型直接根据内角和公式计算可得.
13.如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…这样他以3m/s的速度匀速的一直走下去,他第一次回到出发点A时,一共走了 80 s.
【分析】由题意可知小亮所走的路线为正多边形,根据多边形的外角和定理即可求出答案.
【解答】解:∵小亮从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为n=360°÷15°=24,
则一共走了24×10=240(m),
一共走了240÷3=80(s).
故答案为:80.
【点评】本题主要考查了多边形的外角和定理.任何一个多边形的外角和都是360°,用外角和求正多边形的边数可直接让360°除以一个外角度数即可.
14.已知如图,∠3+∠5+∠7=200°,则∠1+∠2+∠4+∠6+∠8= 200° .
【分析】连结AB、BC、CD,形成一个五边形和三个三角形.由三个三角形内角和和为540°得出(∠3+∠9+∠10)+(∠5+∠11+∠12)+(∠7+∠13+∠14)=180°×3=540°,将∠3+∠5+∠7=200°代入,求出∠9+∠10+∠11+∠12+∠13+∠14=540°﹣200°=340°.由五边形ABCDE的内角和为540°,得出∠1+∠2+∠9+∠10+∠4+∠11+∠12+∠6+∠13+∠14+∠8=540°,将∠9+∠10+∠11+∠12+∠13+∠14=340°代入,即可得出∠1+∠2+∠4+∠6+∠8=540°﹣340°=200°.
【解答】解:如图,连结AB、BC、CD.
∵(∠3+∠9+∠10)+(∠5+∠11+∠12)+(∠7+∠13+∠14)=180°×3=540°,
∴(∠3+∠5+∠7)+(∠9+∠10+∠11+∠12+∠13+∠14)=540°,
∵∠3+∠5+∠7=200°,
∴∠9+∠10+∠11+∠12+∠13+∠14=540°﹣200°=340°.
∵五边形ABCDE的内角和为(5﹣2)×180°=540°,
∴540°=∠1+∠2+∠9+∠10+∠4+∠11+∠12+∠6+∠13+∠14+∠8
=(∠1+∠2+∠4+∠6+∠8)+(∠9+∠10+∠11+∠12+∠13+∠14)
=(∠1+∠2+∠4+∠6+∠8)+340°,
∴∠1+∠2+∠4+∠6+∠8=540°﹣340°=200°.
故答案为200°
【点评】本题考查了多边形内角和定理,难度适中.准确作出辅助线利用数形结合是解题的关键.
15.如果一个多边形的所有内角从小到大排列起来,恰好依次增加相同的度数,设最小角的度数为100°,最大角的度数为140°,那么这个多边形是 六 边形.
【分析】根据内角和公式,设该多边形为n边形,内角和公式为180°?(n﹣2),因为最小角为100°,最大角140°,又依次增加的度数相同,则它的度数应该为.
【解答】解:设该多边形的边数为n.
则为=180?(n﹣2),解得n=6.
故这个多边形为六边形.
【点评】本题思维灵活,也可利用方程解答,方程思想是解多边形有关问题常要用到的思想方法.本题难度不大.
16.在如图一、图二、图三中,分别是由1个、2个、n个正方形连接成的图形.在图1中,x=70°;在图二中,y=28°;通过(1)、(2)的计算,请写出图三中a+b+c+…+d与n的数量关系式 a+b+c+…+d=90°n .
【分析】连接各小正方形的对角线,然后根据正方形的对角线平分一组对角,多边形的内角和公式分别列式求出右边几个角的度数的和,从而找出变化规律即可得解.
【解答】解:如图,连接各小正方形的对角线,
图一中,61°+119°+20°+x+45°×2=360°,
所以,20°+x=360°﹣61°﹣119°﹣45°×2=90°,
图二中,61°+119°+31°+121°+45°×4+y=(5﹣2)?180°,
所以,31°+121°+y=540°﹣61°﹣119°﹣45°×4=180°,
…,
依此类推,a+b+c+…+d=(n+1+2﹣2)?180°﹣45°×2n﹣61°﹣119°=90°n.
故答案为:90°n.
【点评】本题考查了多边形的内角和公式,正方形的对角线平分一组对角的性质,作辅助线构造出多边形是解题的关键.
三.解答题(共7小题)
17.小明在计算一个多边形的内角和,求得的内角和为2220°,经过检查发现少加了一个内角,请问这个内角为多少度?这个多边形是几边形?
【分析】根据多边形的内角和公式(n﹣2)?180°,用2220除以180,商就是n﹣2,余数就是加上的那个外角的度数.进而可以算出这个多边形的边数.
【解答】解:2220÷180=12…60,
则边数n=15,
这个内角的度数是:180°﹣60°=120°.
故这个内角为120度,这个多边形是15边形.
【点评】本题考查多边形内角和公式的灵活运用;关键是找到相应度数的等量关系.
18.已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取720°;而乙同学说,θ也能取820°,甲、乙的说法对吗?若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
【分析】(1)根据多边形内角和公式,列出方程求得θ的值,判断是否为整数即可;
(2)根据题意,列出方程(n﹣2)×180°+360°=(n+x﹣2)×180°,求得x的值即可.
【解答】解:(1)甲对,乙不对.
理由:∵当θ取720°时,720°=(n﹣2)×180°,
解得θ=6;
当θ取820°时,820°=(n﹣2)×180°,
解得θ=;
∵n为整数,
∴θ不能取820°;
(2)依题意得,
(n﹣2)×180°+360°=(n+x﹣2)×180°,
解得x=2.
【点评】本题主要考查了多边形内角和公式,解决问题的关键是掌握多边形内角和公式,解题时注意与多边形外角和的区别.
19.如图,已知四边形ABCD,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,求∠1+∠2的大小.
【分析】根据四边形的内角和为180°,有∠1+∠2+∠FEA1+∠EFB1+∠D+∠C=360°,又,∠C=72°,∠D=81°,则∠FEA1+∠EFB1+∠1+∠2=207°;又∠AEF+∠BFE+∠FEA1+∠EFB1+∠1+∠2=360°,∠FEA1+∠EFB1=∠AEF+∠BFE,即可求出答案.
【解答】解:由题意得:∠1+∠2+∠FEA1+∠EFB1+∠D+∠C=360°,
又∠C=72°,∠D=81°,
则∠FEA1+∠EFB1+∠1+∠2=207°;
又∠AEF+∠BFE+∠FEA1+∠EFB1+∠1+∠2=360°,
又四边形A1B1FE是四边形ABEF翻转得到的,
∴∠FEA1+∠EFB1=∠AEF+∠BFE,
∴∠FEA1+∠EFB1=153°,
∴∠1+∠2=54°.
【点评】本题考查了翻转变换及多边形的内角和的知识,有一定难度,找准各个角的关系是关键.
20.已知凸四边形ABCD中,∠A=∠C=90°.
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明;
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
【分析】(1)DE⊥BF,延长DE交BF于G.易证∠ADC=∠CBM.可得∠CDE=∠EBF.即可得∠EGB=∠C=90゜,则可证得DE⊥BF;
(2)DE∥BF,连接BD,易证∠NDC+∠MBC=180゜,则可得∠EDC+∠CBF=90゜,继而可证得∠EDC+∠CDB+∠CBD+∠FBC=180゜,则可得DE∥BF.
【解答】解:(1)DE⊥BF,
延长DE交BF于点G
∵∠A+∠ABC+∠C+∠ADC=360°
又∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°
∵∠ABC+∠MBC=180°
∴∠ADC=∠MBC,
∵DE、BF分别平分∠ADC、∠MBC
∴∠EDC=∠ADC,∠EBG=∠MBC,
∴∠EDC=∠EBG,
∵∠EDC+∠DEC+∠C=180°
∠EBG+∠BEG+∠EGB=180°
又∵∠DEC=∠BEG∴∠EGB=∠C=90
∴DE⊥BF;
(2)DE∥BF,
连接BD,
∵DE、BF分别平分∠NDC、∠MBC
∴∠EDC=∠NDC,∠FBC=∠MBC,
∵∠ADC+∠NDC=180°
又∵∠ADC=∠MBC
∴∠MBC+∠NDC=180°
∴∠EDC+∠FBC=90°,
∵∠C=90°∴∠CDB+∠CBD=90°
∴∠EDC+∠CDB+∠FBC+∠CBD=180°
即∠EDB+∠FBD=180°,
∴DE∥BF.
【点评】此题考查了三角形内角和定理,平行线的性质以及三角形外角的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
21.四边形ABCD中,∠A=145°,∠D=75°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
【分析】(1)根据四边形的内角和即可得到结论;
(2)根据平行线的性质得到∠ABE=35°,∠BED=105°,由∠ABC的角平分线BE交DC于点E,得到∠CBE=∠ABE=35°,根据三角形的外角的性质即可得到结论;
(3)根据四边形的性质得到∠ABC+∠BCD=140°,根据三角形的内角和即可得到结论.
【解答】解:(1)∵∠A=145°,∠D=75°,
∴∠B=∠C=(360°﹣145°﹣75°)=70°;
(2)∵BE∥AD,∠A=145°,∠D=75°,
∴∠ABE=180°﹣∠A=35°,∠BED=180°﹣∠D=105°,
∵∠ABC的角平分线BE交DC于点E,
∴∠CBE=∠ABE=35°,
∴∠C=∠BED﹣∠EBC=70°;
(3)∵∠A=145°,∠D=75°,
∴∠ABC+∠BCD=360°﹣∠A﹣∠D=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=(∠ABC+∠DCB)=70°,
∴∠BEC=110°.
【点评】本题主要考查了三角形的内角和,多边形的内角和定理等知识点的理解和掌握,能求出∠ABC+∠DCB的度数是解此题的关键.
22.如图,△ADE和△ABC中∠EAD=∠AED=∠BAC=∠BCA=45°,又有∠BAD=∠BCF.
(1)求∠ECF+DAC+∠ECA的度数;
(2)判断ED与FC的位置关系,并对你的结论加以证明.
【分析】(1)由题意易得∠ECF+DAC+∠ECA=45°+∠BCF+45°﹣∠BCF=90°;
(2)由凹四边形ADEC得内角和是360°以及已知易得∠ADE=90°,可得∠ECA+∠CED+∠CAD=∠EDA=90°,又(1)的结论是∠ECF+DAC+∠ECA=90°,∴∠CED=∠ECF,因此由内错角相等即知DE∥CF.
【解答】解:(1)∵∠ECF=∠ECB+∠BCF,
∴∠ECF+∠DAC+∠ECA
=(∠ECB+∠BCF)+∠DAC+∠ECA (∠BCF=∠BAD)
=(∠ECB+∠ECA)+(∠DAC+∠BAD)
=∠BCA+∠BAC
=45°+45°
=90°
即∠ECF+DAC+∠ECA=90°;
(2)ED和FC平行,理由如下:
∵∠EAD=∠AED=45°,
∴∠EDA=90°,
∴在C,E,D,A四点组成的凹四边形里,
∠ECA+∠CED+∠CAD=∠EDA=90°
又∵(1)的结论是∠ECF+DAC+∠ECA=90°,
∴∠CED=∠ECF,
∴DE∥CF(内错角相等,两直线平行).
【点评】此题主要考查了角之间的和差关系、四边形的内角和、平行线的判定等知识点,有点难度,特别是凹四边形的应用不太常见.
23.已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=100°,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,则∠ABD+∠ACD= 240 度
(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由;
(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论 不能 .(填“能”或“不能”)
【分析】(1)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠CBD+∠ACB+∠BCD,利用三角形内角和定理得出∠ABC+∠ACB=180°﹣∠A=180°﹣40°=140°;根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=100°,∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°;
(2)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠ACB﹣(∠BCD+∠CBD)的度数.根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=100°;根据三角形内角和定理得,∠ABC+∠ACB=180°﹣∠A=140°,∴∠ABD+∠ACD=∠ABC+∠ACB﹣(∠BCD+∠CBD)=140°﹣100°=40°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
【解答】解:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°
∴∠ABC+∠ACB=180°﹣40°=140°
在△BCD中,∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°﹣∠D
在△DEF中,∠D+∠E+∠F=180°
∴∠E+∠F=180°﹣∠D
∴∠CBD+∠BCD=∠E+∠F=100°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°.
故答案为:240°;
(2)∠ABD+∠ACD=40°;
理由如下:
∵∠E+∠F=100°
∴∠D=180°﹣(∠E+∠F)=80°
∴∠ABD+∠ACD=180°﹣∠A﹣∠DBC﹣∠DCB
=180°﹣40°﹣(180°﹣80°)
=40°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
故答案为:不能.
【点评】考查三角形内角和定理,外角性质.熟练掌握这些性质是解题的关键.
一.选择题(共10小题)
1.如果一个正多边形的一个内角是140°,那么这个正多边形的边数是( )
A.10 B.9 C.8 D.7
2.当多边形边数增加一条时,多边形的内、外角和的变化情况是( )
A.内角和、外角和都不变 B.内角和、外角和各增加180°
C.内角和不变,外角和增加180° D.内角和增加180°,外角和不变
3.一个多边形的内角都相等,它的每一个外角都等于45度,则该多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
4.如图1是四边形纸片ABCD,其中∠B=120°,∠D=50°.如果将其右下角向内折出△PCR,如图2所示,恰使CP∥AB,RC∥AD,则∠C的度数为( )
A.105° B.100° C.95° D.90°
5.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
6.如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
A.40° B.45° C.50° D.60°
7.如图,小明将几块六边形纸片分别减掉了一部分(虚线部分),得到了一个新多边形.若新多边形的内角和为540°,则对应的是下列哪个图形( )
A. B. C. D.
8.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=85°,则∠DPE=( )
A.100° B.130° C.120° D.95°
9.如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )
A.240° B.120° C.230° D.200°
10.如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )
A.600° B.700° C.720° D.800°
二.填空题(共6小题)
11.如图,有一条公共边的正六边形和正方形如图放置,则∠α= 度.
12.如图所示,则(∠1+∠2﹣∠3)+(∠4+∠5﹣∠6)+(∠7+∠8﹣∠9)= 度.
13.如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…这样他以3m/s的速度匀速的一直走下去,他第一次回到出发点A时,一共走了 s.
14.已知如图,∠3+∠5+∠7=200°,则∠1+∠2+∠4+∠6+∠8= .
15.如果一个多边形的所有内角从小到大排列起来,恰好依次增加相同的度数,设最小角的度数为100°,最大角的度数为140°,那么这个多边形是 边形.
16.在如图一、图二、图三中,分别是由1个、2个、n个正方形连接成的图形.在图1中,x=70°;在图二中,y=28°;通过(1)、(2)的计算,请写出图三中a+b+c+…+d与n的数量关系式 .
三.解答题(共7小题)
17.小明在计算一个多边形的内角和,求得的内角和为2220°,经过检查发现少加了一个内角,请问这个内角为多少度?这个多边形是几边形?
18.已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取720°;而乙同学说,θ也能取820°,甲、乙的说法对吗?若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
19.如图,已知四边形ABCD,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,求∠1+∠2的大小.
20.已知凸四边形ABCD中,∠A=∠C=90°.
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明;
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
21.四边形ABCD中,∠A=145°,∠D=75°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
22.如图,△ADE和△ABC中∠EAD=∠AED=∠BAC=∠BCA=45°,又有∠BAD=∠BCF.
(1)求∠ECF+DAC+∠ECA的度数;
(2)判断ED与FC的位置关系,并对你的结论加以证明.
23.已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=100°,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,则∠ABD+∠ACD= 度
(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由;
(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论 .(填“能”或“不能”)
【走进重高汇编】八上数学第十一章 多边形及其内角和(第3节)
参考答案与试题解析
一.选择题(共10小题)
1.如果一个正多边形的一个内角是140°,那么这个正多边形的边数是( )
A.10 B.9 C.8 D.7
【分析】根据多边形的内角和公式(n﹣2)?180°列式进行计算即可得解.
【解答】解:设这个正多边形的边数是n,
根据题意得,(n﹣2)?180°=140°?n,
解得n=9.故选:B.
2.当多边形边数增加一条时,多边形的内、外角和的变化情况是( )
A.内角和、外角和都不变 B.内角和、外角和各增加180°
C.内角和不变,外角和增加180° D.内角和增加180°,外角和不变
【分析】根据多边形的内角和定理以及外角和等于360°,计算后直接选择答案.
【解答】解:∵多边形内角和为(n﹣2)?180°,外角和为360°,
∴多边形边数增加一条,内角和增加180°,外角和不变.
故选:D.
3.一个多边形的内角都相等,它的每一个外角都等于45度,则该多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
【分析】先利用360°÷45°求出多边形的边数即可求解.
【解答】解:多边形的边数为:360°÷45°=8,
故选:C.
4.如图1是四边形纸片ABCD,其中∠B=120°,∠D=50°.如果将其右下角向内折出△PCR,如图2所示,恰使CP∥AB,RC∥AD,则∠C的度数为( )
A.105° B.100° C.95° D.90°
【分析】根据平行线的性质得∠BPC=180°﹣∠B=60°,∠DRC=130°,再利用三角形的内角和求出∠C的度数.
【解答】解:∵CP∥AB,RC∥AD
∴∠BPC=180°﹣∠B=60°,∠DRC=130°
∴∠C=180°﹣60°﹣25°=95°.
故选:C.
5.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
【分析】首先求得内角和为1080°的多边形的边数,即可确定原多边形的边数.
【解答】解:设内角和为1080°的多边形的边数是n,则(n﹣2)?180°=1080°,
解得:n=8.
则原多边形的边数为7或8或9.
故选:D.
6.如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
A.40° B.45° C.50° D.60°
【分析】在DO延长线上找一点M,根据多边形的外角和为360°可得出∠BOM=140°,再根据邻补角互补即可得出结论.
【解答】解:在DO延长线上找一点M,如图所示.
∵多边形的外角和为360°,
∴∠BOM=360°﹣220°=140°.
∵∠BOD+∠BOM=180°,
∴∠BOD=180°﹣∠BOM=180°﹣140°=40°.
故选:A.
【点评】本题考查了多边形的内角与外角以及邻补角,解题的关键是根据多边形的外角和为360°找出∠BOM=140°.
7.如图,小明将几块六边形纸片分别减掉了一部分(虚线部分),得到了一个新多边形.若新多边形的内角和为540°,则对应的是下列哪个图形( )
A. B. C. D.
【分析】根据新多边形的内角和为540°,n边形的内角和公式为(n﹣2)?180°,由此列方程求n.
【解答】解:设这个新多边形的边数是n,
则(n﹣2)?180°=540°,
解得:n=5,
故选:C.
【点评】本题考查了多边形外角与内角.此题比较简单,只要结合多边形的内角和公式来寻求等量关系,构建方程即可求解.
8.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=85°,则∠DPE=( )
A.100° B.130° C.120° D.95°
【分析】根据三角形的高的定义可得∠ADC=∠AEB=90°,再根据四边形内角和为360°可得∠DPE=360°﹣90°﹣90°﹣85°=95°.
【解答】解:∵CD,BE分别是AB,AC边上的高,
∴∠ADC=∠AEB=90°,
∵∠A=85°,
∴∠DPE=360°﹣90°﹣90°﹣85°=95°,
故选:D.
【点评】此题主要考查了多边形的内角,以及三角形的高,关键是掌握四边形内角和为360°.
9.如图,从△ABC纸片中剪去△CDE,得到四边形ABDE,若∠C=60°.则∠1+∠2等于( )
A.240° B.120° C.230° D.200°
【分析】根据题意可得出∠B+∠A,再根据四边形的内角和定理可求出∠1+∠2.
【解答】解:∵∠C=60°,
∴∠B+∠A=120°,
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=240°,
故选:A.
【点评】本题考查了三角形的内角和定理,四边形的内角和定理,三角形的内角和等于180°,解决本题的关键是求出∠B+∠A.
10.如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )
A.600° B.700° C.720° D.800°
【分析】先根据四边形内角和等于360°得出∠D的度数,根据三角形内角和定理和折叠的性质可以分别得到∠1+∠2,∠3+∠4,∠5+∠6的度数,根据三角形外角的性质和折叠的性质可以得到∠7﹣∠8的度数,再相加即可求解.
【解答】解:∵四边形ABCD中,∠A=160°,∠B=30°,∠C=60°,
∴∠D=360°﹣160°﹣30°﹣60°=110°,
∴∠1+∠2=360°﹣(180°﹣160°)×2=320°,
∠3+∠4=360°﹣(180°﹣110°)×2=220°,
∠5+∠6=360°﹣(180°﹣60°)×2=120°,
∠7﹣∠8=﹣(∠B+∠B′)=﹣60°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8
=320°+220°+120°﹣60°
=600°.
故选:A.
【点评】考查了四边形内角和等于360°,三角形内角和定理,折叠的性质,以及三角形外角的性质的综合应用.
二.填空题(共6小题)
11.如图,有一条公共边的正六边形和正方形如图放置,则∠α= 150 度.
【分析】求出正六边形和正方形的内角的度数,这两个角的度数与∠α的和是360°,即可求得.
【解答】解:正六边形的内角是:(6﹣2)?180÷6=120°;
正方形的角是90度.
则∠α=360﹣120﹣90=150°.
故答案为:150°.
【点评】本题主要考查了正多边形的内角和定理,n边形的内角和是(n﹣2)?180°.
12.如图所示,则(∠1+∠2﹣∠3)+(∠4+∠5﹣∠6)+(∠7+∠8﹣∠9)= 180 度.
【分析】利用多边形的内角和公式即可求出答案.
【解答】解:∵∠1+∠2+(360°﹣∠3)+∠4+∠5+(360°﹣∠6)+∠7+∠8+(360°﹣∠9)=180°?(9﹣2)=1260度,
∴(∠1+∠2﹣∠3)+(∠4+∠5﹣∠6)+(∠7+∠8﹣∠9)=1260﹣360×3=180°.
【点评】主要考查了多边形的内角和定理.n边形的内角和为:180°(n﹣2).此类题型直接根据内角和公式计算可得.
13.如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…这样他以3m/s的速度匀速的一直走下去,他第一次回到出发点A时,一共走了 80 s.
【分析】由题意可知小亮所走的路线为正多边形,根据多边形的外角和定理即可求出答案.
【解答】解:∵小亮从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为n=360°÷15°=24,
则一共走了24×10=240(m),
一共走了240÷3=80(s).
故答案为:80.
【点评】本题主要考查了多边形的外角和定理.任何一个多边形的外角和都是360°,用外角和求正多边形的边数可直接让360°除以一个外角度数即可.
14.已知如图,∠3+∠5+∠7=200°,则∠1+∠2+∠4+∠6+∠8= 200° .
【分析】连结AB、BC、CD,形成一个五边形和三个三角形.由三个三角形内角和和为540°得出(∠3+∠9+∠10)+(∠5+∠11+∠12)+(∠7+∠13+∠14)=180°×3=540°,将∠3+∠5+∠7=200°代入,求出∠9+∠10+∠11+∠12+∠13+∠14=540°﹣200°=340°.由五边形ABCDE的内角和为540°,得出∠1+∠2+∠9+∠10+∠4+∠11+∠12+∠6+∠13+∠14+∠8=540°,将∠9+∠10+∠11+∠12+∠13+∠14=340°代入,即可得出∠1+∠2+∠4+∠6+∠8=540°﹣340°=200°.
【解答】解:如图,连结AB、BC、CD.
∵(∠3+∠9+∠10)+(∠5+∠11+∠12)+(∠7+∠13+∠14)=180°×3=540°,
∴(∠3+∠5+∠7)+(∠9+∠10+∠11+∠12+∠13+∠14)=540°,
∵∠3+∠5+∠7=200°,
∴∠9+∠10+∠11+∠12+∠13+∠14=540°﹣200°=340°.
∵五边形ABCDE的内角和为(5﹣2)×180°=540°,
∴540°=∠1+∠2+∠9+∠10+∠4+∠11+∠12+∠6+∠13+∠14+∠8
=(∠1+∠2+∠4+∠6+∠8)+(∠9+∠10+∠11+∠12+∠13+∠14)
=(∠1+∠2+∠4+∠6+∠8)+340°,
∴∠1+∠2+∠4+∠6+∠8=540°﹣340°=200°.
故答案为200°
【点评】本题考查了多边形内角和定理,难度适中.准确作出辅助线利用数形结合是解题的关键.
15.如果一个多边形的所有内角从小到大排列起来,恰好依次增加相同的度数,设最小角的度数为100°,最大角的度数为140°,那么这个多边形是 六 边形.
【分析】根据内角和公式,设该多边形为n边形,内角和公式为180°?(n﹣2),因为最小角为100°,最大角140°,又依次增加的度数相同,则它的度数应该为.
【解答】解:设该多边形的边数为n.
则为=180?(n﹣2),解得n=6.
故这个多边形为六边形.
【点评】本题思维灵活,也可利用方程解答,方程思想是解多边形有关问题常要用到的思想方法.本题难度不大.
16.在如图一、图二、图三中,分别是由1个、2个、n个正方形连接成的图形.在图1中,x=70°;在图二中,y=28°;通过(1)、(2)的计算,请写出图三中a+b+c+…+d与n的数量关系式 a+b+c+…+d=90°n .
【分析】连接各小正方形的对角线,然后根据正方形的对角线平分一组对角,多边形的内角和公式分别列式求出右边几个角的度数的和,从而找出变化规律即可得解.
【解答】解:如图,连接各小正方形的对角线,
图一中,61°+119°+20°+x+45°×2=360°,
所以,20°+x=360°﹣61°﹣119°﹣45°×2=90°,
图二中,61°+119°+31°+121°+45°×4+y=(5﹣2)?180°,
所以,31°+121°+y=540°﹣61°﹣119°﹣45°×4=180°,
…,
依此类推,a+b+c+…+d=(n+1+2﹣2)?180°﹣45°×2n﹣61°﹣119°=90°n.
故答案为:90°n.
【点评】本题考查了多边形的内角和公式,正方形的对角线平分一组对角的性质,作辅助线构造出多边形是解题的关键.
三.解答题(共7小题)
17.小明在计算一个多边形的内角和,求得的内角和为2220°,经过检查发现少加了一个内角,请问这个内角为多少度?这个多边形是几边形?
【分析】根据多边形的内角和公式(n﹣2)?180°,用2220除以180,商就是n﹣2,余数就是加上的那个外角的度数.进而可以算出这个多边形的边数.
【解答】解:2220÷180=12…60,
则边数n=15,
这个内角的度数是:180°﹣60°=120°.
故这个内角为120度,这个多边形是15边形.
【点评】本题考查多边形内角和公式的灵活运用;关键是找到相应度数的等量关系.
18.已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取720°;而乙同学说,θ也能取820°,甲、乙的说法对吗?若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
【分析】(1)根据多边形内角和公式,列出方程求得θ的值,判断是否为整数即可;
(2)根据题意,列出方程(n﹣2)×180°+360°=(n+x﹣2)×180°,求得x的值即可.
【解答】解:(1)甲对,乙不对.
理由:∵当θ取720°时,720°=(n﹣2)×180°,
解得θ=6;
当θ取820°时,820°=(n﹣2)×180°,
解得θ=;
∵n为整数,
∴θ不能取820°;
(2)依题意得,
(n﹣2)×180°+360°=(n+x﹣2)×180°,
解得x=2.
【点评】本题主要考查了多边形内角和公式,解决问题的关键是掌握多边形内角和公式,解题时注意与多边形外角和的区别.
19.如图,已知四边形ABCD,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,求∠1+∠2的大小.
【分析】根据四边形的内角和为180°,有∠1+∠2+∠FEA1+∠EFB1+∠D+∠C=360°,又,∠C=72°,∠D=81°,则∠FEA1+∠EFB1+∠1+∠2=207°;又∠AEF+∠BFE+∠FEA1+∠EFB1+∠1+∠2=360°,∠FEA1+∠EFB1=∠AEF+∠BFE,即可求出答案.
【解答】解:由题意得:∠1+∠2+∠FEA1+∠EFB1+∠D+∠C=360°,
又∠C=72°,∠D=81°,
则∠FEA1+∠EFB1+∠1+∠2=207°;
又∠AEF+∠BFE+∠FEA1+∠EFB1+∠1+∠2=360°,
又四边形A1B1FE是四边形ABEF翻转得到的,
∴∠FEA1+∠EFB1=∠AEF+∠BFE,
∴∠FEA1+∠EFB1=153°,
∴∠1+∠2=54°.
【点评】本题考查了翻转变换及多边形的内角和的知识,有一定难度,找准各个角的关系是关键.
20.已知凸四边形ABCD中,∠A=∠C=90°.
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明;
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
【分析】(1)DE⊥BF,延长DE交BF于G.易证∠ADC=∠CBM.可得∠CDE=∠EBF.即可得∠EGB=∠C=90゜,则可证得DE⊥BF;
(2)DE∥BF,连接BD,易证∠NDC+∠MBC=180゜,则可得∠EDC+∠CBF=90゜,继而可证得∠EDC+∠CDB+∠CBD+∠FBC=180゜,则可得DE∥BF.
【解答】解:(1)DE⊥BF,
延长DE交BF于点G
∵∠A+∠ABC+∠C+∠ADC=360°
又∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°
∵∠ABC+∠MBC=180°
∴∠ADC=∠MBC,
∵DE、BF分别平分∠ADC、∠MBC
∴∠EDC=∠ADC,∠EBG=∠MBC,
∴∠EDC=∠EBG,
∵∠EDC+∠DEC+∠C=180°
∠EBG+∠BEG+∠EGB=180°
又∵∠DEC=∠BEG∴∠EGB=∠C=90
∴DE⊥BF;
(2)DE∥BF,
连接BD,
∵DE、BF分别平分∠NDC、∠MBC
∴∠EDC=∠NDC,∠FBC=∠MBC,
∵∠ADC+∠NDC=180°
又∵∠ADC=∠MBC
∴∠MBC+∠NDC=180°
∴∠EDC+∠FBC=90°,
∵∠C=90°∴∠CDB+∠CBD=90°
∴∠EDC+∠CDB+∠FBC+∠CBD=180°
即∠EDB+∠FBD=180°,
∴DE∥BF.
【点评】此题考查了三角形内角和定理,平行线的性质以及三角形外角的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
21.四边形ABCD中,∠A=145°,∠D=75°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
【分析】(1)根据四边形的内角和即可得到结论;
(2)根据平行线的性质得到∠ABE=35°,∠BED=105°,由∠ABC的角平分线BE交DC于点E,得到∠CBE=∠ABE=35°,根据三角形的外角的性质即可得到结论;
(3)根据四边形的性质得到∠ABC+∠BCD=140°,根据三角形的内角和即可得到结论.
【解答】解:(1)∵∠A=145°,∠D=75°,
∴∠B=∠C=(360°﹣145°﹣75°)=70°;
(2)∵BE∥AD,∠A=145°,∠D=75°,
∴∠ABE=180°﹣∠A=35°,∠BED=180°﹣∠D=105°,
∵∠ABC的角平分线BE交DC于点E,
∴∠CBE=∠ABE=35°,
∴∠C=∠BED﹣∠EBC=70°;
(3)∵∠A=145°,∠D=75°,
∴∠ABC+∠BCD=360°﹣∠A﹣∠D=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=(∠ABC+∠DCB)=70°,
∴∠BEC=110°.
【点评】本题主要考查了三角形的内角和,多边形的内角和定理等知识点的理解和掌握,能求出∠ABC+∠DCB的度数是解此题的关键.
22.如图,△ADE和△ABC中∠EAD=∠AED=∠BAC=∠BCA=45°,又有∠BAD=∠BCF.
(1)求∠ECF+DAC+∠ECA的度数;
(2)判断ED与FC的位置关系,并对你的结论加以证明.
【分析】(1)由题意易得∠ECF+DAC+∠ECA=45°+∠BCF+45°﹣∠BCF=90°;
(2)由凹四边形ADEC得内角和是360°以及已知易得∠ADE=90°,可得∠ECA+∠CED+∠CAD=∠EDA=90°,又(1)的结论是∠ECF+DAC+∠ECA=90°,∴∠CED=∠ECF,因此由内错角相等即知DE∥CF.
【解答】解:(1)∵∠ECF=∠ECB+∠BCF,
∴∠ECF+∠DAC+∠ECA
=(∠ECB+∠BCF)+∠DAC+∠ECA (∠BCF=∠BAD)
=(∠ECB+∠ECA)+(∠DAC+∠BAD)
=∠BCA+∠BAC
=45°+45°
=90°
即∠ECF+DAC+∠ECA=90°;
(2)ED和FC平行,理由如下:
∵∠EAD=∠AED=45°,
∴∠EDA=90°,
∴在C,E,D,A四点组成的凹四边形里,
∠ECA+∠CED+∠CAD=∠EDA=90°
又∵(1)的结论是∠ECF+DAC+∠ECA=90°,
∴∠CED=∠ECF,
∴DE∥CF(内错角相等,两直线平行).
【点评】此题主要考查了角之间的和差关系、四边形的内角和、平行线的判定等知识点,有点难度,特别是凹四边形的应用不太常见.
23.已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=100°,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,则∠ABD+∠ACD= 240 度
(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由;
(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论 不能 .(填“能”或“不能”)
【分析】(1)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠CBD+∠ACB+∠BCD,利用三角形内角和定理得出∠ABC+∠ACB=180°﹣∠A=180°﹣40°=140°;根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=100°,∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°;
(2)要求∠ABD+∠ACD的度数,只要求出∠ABC+∠ACB﹣(∠BCD+∠CBD)的度数.根据三角形内角和定理,∠CBD+∠BCD=∠E+∠F=100°;根据三角形内角和定理得,∠ABC+∠ACB=180°﹣∠A=140°,∴∠ABD+∠ACD=∠ABC+∠ACB﹣(∠BCD+∠CBD)=140°﹣100°=40°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
【解答】解:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°
∴∠ABC+∠ACB=180°﹣40°=140°
在△BCD中,∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°﹣∠D
在△DEF中,∠D+∠E+∠F=180°
∴∠E+∠F=180°﹣∠D
∴∠CBD+∠BCD=∠E+∠F=100°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°.
故答案为:240°;
(2)∠ABD+∠ACD=40°;
理由如下:
∵∠E+∠F=100°
∴∠D=180°﹣(∠E+∠F)=80°
∴∠ABD+∠ACD=180°﹣∠A﹣∠DBC﹣∠DCB
=180°﹣40°﹣(180°﹣80°)
=40°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.则∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
故答案为:不能.
【点评】考查三角形内角和定理,外角性质.熟练掌握这些性质是解题的关键.
