(沪科版选修3-1)物理:5.5《探究洛伦兹力》测试(2)
文档属性
| 名称 | (沪科版选修3-1)物理:5.5《探究洛伦兹力》测试(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 58.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2010-08-31 00:00:00 | ||
图片预览


文档简介
5.5探究洛伦兹力 测试
1、一个电子以一定初速度进入一匀强场区(只有电场或只有磁场不计其他作用)并保持匀速率运动,下列说法正确的是( )
A.电子速率不变,说明不受场力作用
B.电子速率不变,不可能是进入电场
C.电子可能是进入电场,且在等势面上运动
D.电子一定是进入磁场,且做的圆周运动
2、如图—10所示,正交的电磁场区域中,有
两个质量相同、带同种电荷的带电粒子,电量分别为
qa、qb.它们沿水平方向以相同的速率相对着匀速直线
穿过电磁场区,则( )
A.它们带负电,且qa>qb. B.它们带负带电,qa <qb
C.它们带正电,且qa>qb. D.它们带正电,且qa <qb. . 图-10
3、如图—9所示,带正电的小球穿在绝缘粗糙直杆上,
杆倾角为θ,整个空间存在着竖直向上的匀强电场和垂直于杆斜向上的匀强磁场,小球沿杆向下运动,在a点时动能
为100J,到C点动能为零,而b点恰为a、c的中点,
在此运动过程中( )
A.小球经b点时动能为50J 图—9
B.小球电势能增加量可能大于其重力势能减少量
C.小球在ab段克服摩擦所做的功与在bc段克服摩擦所做的功相等
D.小球到C点后可能沿杆向上运动。
4、如图所示,竖直向下的匀强磁场穿过光滑的绝缘水平面,平面上一个钉子O固定一根细线,细线的另一端系一带电小球,小球在光滑水平面内绕O做匀速圆周运动.在某时刻细线断开,小球仍然在匀强磁场中做匀速圆周运动,下列说法一定错误的是( )
A.速率变小,半径变小,周期不变
B.速率不变,半径不变,周期不变
C.速率不变,半径变大,周期变大
D.速率不变,半径变小,周期变小
5、如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中( )
A.运动时间相同
B.运动轨道半径相同
C.重新回到x轴时速度大小和方向均相同
D.重新回到x轴时距O点的距离相同
6、 质量为0.1kg、带电量为2.5×10—8C的质点,置于水平的匀强磁场中,磁感强度的方向为南指向北,大小为0.65T.为保持此质量不下落,必须使它沿水平面运动,它的速度方向为_____________,大小为______________。
7、如图—20所示,水平放置的平行金属板A带正电,B带负电,A、B间距离为d.匀强磁场的磁感强度为B,方向垂直纸面向里.今有一带电粒子在A、B间竖直平面内做半径为R的匀速圆周运动.则带电粒子转动方向为_________时针方向,速率υ=_________.
图—20
8、电子自静止开始经M、N板间(两板间的电压为u)的电场加速后从A点垂直于磁场边界射入宽度为d的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求匀强磁场的磁感应强度.(已知电子的质量为m,电量为e)
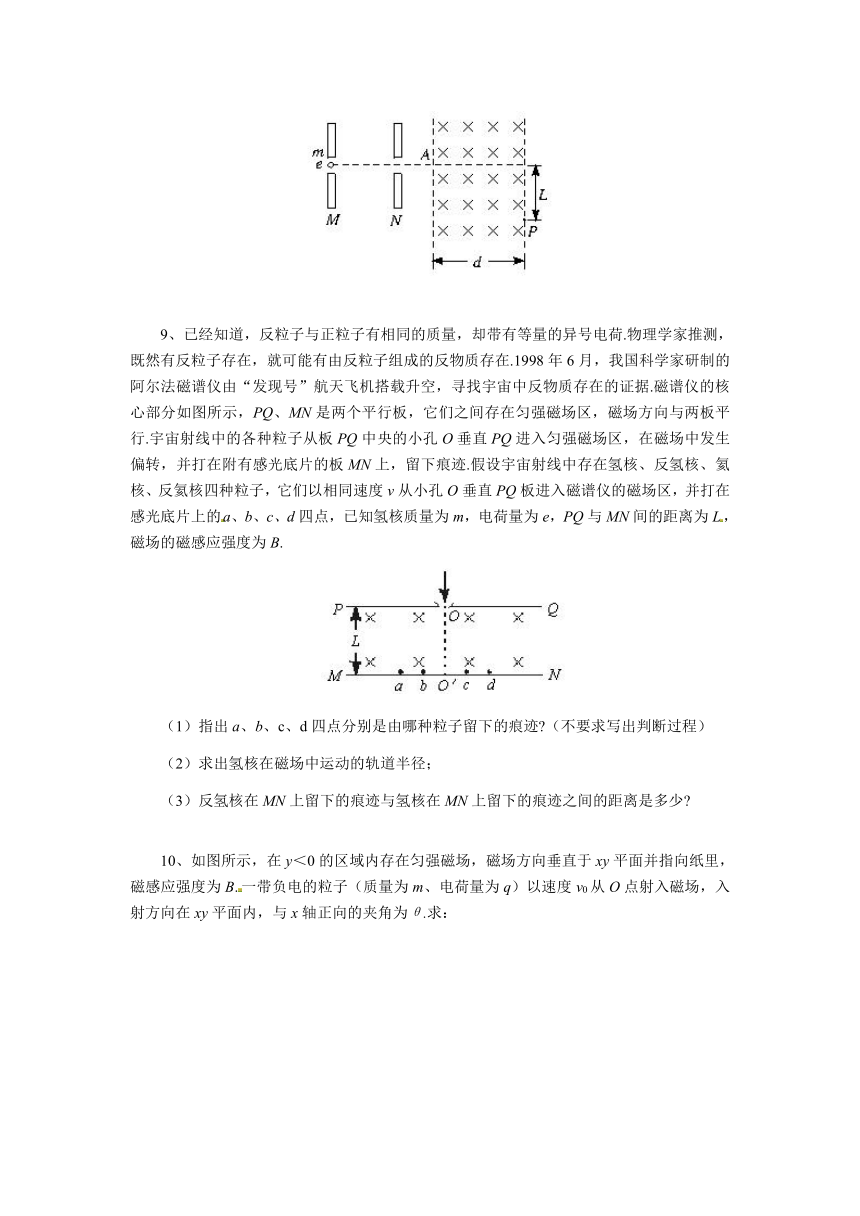
9、已经知道,反粒子与正粒子有相同的质量,却带有等量的异号电荷.物理学家推测,既然有反粒子存在,就可能有由反粒子组成的反物质存在.1998年6月,我国科学家研制的阿尔法磁谱仪由“发现号”航天飞机搭载升空,寻找宇宙中反物质存在的证据.磁谱仪的核心部分如图所示,PQ、MN是两个平行板,它们之间存在匀强磁场区,磁场方向与两板平行.宇宙射线中的各种粒子从板PQ中央的小孔O垂直PQ进入匀强磁场区,在磁场中发生偏转,并打在附有感光底片的板MN上,留下痕迹.假设宇宙射线中存在氢核、反氢核、氦核、反氦核四种粒子,它们以相同速度v从小孔O垂直PQ板进入磁谱仪的磁场区,并打在感光底片上的a、b、c、d四点,已知氢核质量为m,电荷量为e,PQ与MN间的距离为L,磁场的磁感应强度为B.
(1)指出a、b、c、d四点分别是由哪种粒子留下的痕迹 (不要求写出判断过程)
(2)求出氢核在磁场中运动的轨道半径;
(3)反氢核在MN上留下的痕迹与氢核在MN上留下的痕迹之间的距离是多少
10、如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸里,磁感应强度为B.一带负电的粒子(质量为m、电荷量为q)以速度v0从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.求:
(1)该粒子射出磁场的位置;
(2)该粒子在磁场中运动的时间.(粒子所受重力不计)
11、如图—23所示,套在足够长的固定绝
缘直棒上的小球,质量为10—4kg,带有4×10—4C
的正电,小球可沿棒滑动,动摩擦因数为0.2。把
此棒竖直地放在互相垂直且境外沿水平方向的匀
强电场和匀强磁场中,电场强度为10N/C,磁感
强度为0.5T.求小球由静止释放后下落过程中的最
大加速度和最大速度(g取10m/s2)
12、如图—24所示,在一坐标系内,x轴
上方有磁感强度为B的匀强磁场,下方有电场强
度为E的匀强电场。今有质量为m、电量为q的
带电粒子从y轴上某处静止释放后 恰能经过x
轴上的距原点O为l的P点,不计重力。
(1)粒子带的是什么电?
(2)释放点离原点O的距离应满足什么条件?
(3)从释放点到P点,粒子一共经历多长时间?
13.如图1-3-18所示, 磁感强度为B的均匀磁场中,固定放置一绝缘材料制成的边长为L的刚性等边三角形,其平面与磁场方向垂直,在DE边上的S点(DS=L/4)处带电粒子的放射源,发射粒子的方向皆在图中纸面内垂直DE边向下,发射粒子的电量皆为q(q>0),质量皆为m,但速度v有各种不同的数值,若这些粒子与框架的碰撞时均无能量损失,并要求每一次碰撞时速度方向垂直于被碰的边,试问
(1)带电粒子速度v取哪些值时可使S点发出的粒子最终又回到S点?
(2)这些粒子中,回到S点所用时间最短为多少?(重力不计,磁场范围足够大)
参 考 答 案
1、C 2、D 3、BD 4、A 5、BCD 6、(向右,6×104m/s) 7、(顺,BRg/E)
8、解析:电子在M、N间加速后获得的速度为v,由动能定理得:
mv2-0=eu
电子进入磁场后做匀速圆周运动,设其半径为r,则:
evB=m
电子在磁场中的轨迹如图,由几何得:
=
由以上三式得:B=
9、解:(1)a、b、c、d四点分别是反氢核、反氦核、氦核和氢核留下的痕迹.
(2)对氢核,在磁场中做匀速圆周运动,由牛顿第二定律得:
(3)由图中几何关系知:
所以反氢核与氢核留下的痕迹之间的距离
10、解:(1)带负电粒子射入磁场后,由于受到洛伦兹力的作用,粒子将沿图示的轨迹运动,从A点射出磁场,设O、A间的距离为L,射出时速度的大小仍为v,射出方向与x轴的夹角仍为θ,由洛伦兹力公式和牛顿定律可得:
qv0B=m 式中R为圆轨道半径,解得:
R= ①
圆轨道的圆心位于OA的中垂线上,由几何关系可得:
=Rsinθ ②
联解①②两式,得:L=
所以粒子离开磁场的位置坐标为(-,0)
(2)因为T==
所以粒子在磁场中运动的时间,t=
11、am=2m/s2,υm=5m/s
12、(1)负电
(2)d=qL2B2/(8Mek2) (K=1,2,3……)
(3)t=+ (K=1,2,3……)
13.(1)vn=(n=1,2,3…) (2) tmin =
F
E
D
S
图1-3-18
1、一个电子以一定初速度进入一匀强场区(只有电场或只有磁场不计其他作用)并保持匀速率运动,下列说法正确的是( )
A.电子速率不变,说明不受场力作用
B.电子速率不变,不可能是进入电场
C.电子可能是进入电场,且在等势面上运动
D.电子一定是进入磁场,且做的圆周运动
2、如图—10所示,正交的电磁场区域中,有
两个质量相同、带同种电荷的带电粒子,电量分别为
qa、qb.它们沿水平方向以相同的速率相对着匀速直线
穿过电磁场区,则( )
A.它们带负电,且qa>qb. B.它们带负带电,qa <qb
C.它们带正电,且qa>qb. D.它们带正电,且qa <qb. . 图-10
3、如图—9所示,带正电的小球穿在绝缘粗糙直杆上,
杆倾角为θ,整个空间存在着竖直向上的匀强电场和垂直于杆斜向上的匀强磁场,小球沿杆向下运动,在a点时动能
为100J,到C点动能为零,而b点恰为a、c的中点,
在此运动过程中( )
A.小球经b点时动能为50J 图—9
B.小球电势能增加量可能大于其重力势能减少量
C.小球在ab段克服摩擦所做的功与在bc段克服摩擦所做的功相等
D.小球到C点后可能沿杆向上运动。
4、如图所示,竖直向下的匀强磁场穿过光滑的绝缘水平面,平面上一个钉子O固定一根细线,细线的另一端系一带电小球,小球在光滑水平面内绕O做匀速圆周运动.在某时刻细线断开,小球仍然在匀强磁场中做匀速圆周运动,下列说法一定错误的是( )
A.速率变小,半径变小,周期不变
B.速率不变,半径不变,周期不变
C.速率不变,半径变大,周期变大
D.速率不变,半径变小,周期变小
5、如图所示,x轴上方有垂直纸面向里的匀强磁场.有两个质量相同,电荷量也相同的带正、负电的离子(不计重力),以相同速度从O点射入磁场中,射入方向与x轴均夹θ角.则正、负离子在磁场中( )
A.运动时间相同
B.运动轨道半径相同
C.重新回到x轴时速度大小和方向均相同
D.重新回到x轴时距O点的距离相同
6、 质量为0.1kg、带电量为2.5×10—8C的质点,置于水平的匀强磁场中,磁感强度的方向为南指向北,大小为0.65T.为保持此质量不下落,必须使它沿水平面运动,它的速度方向为_____________,大小为______________。
7、如图—20所示,水平放置的平行金属板A带正电,B带负电,A、B间距离为d.匀强磁场的磁感强度为B,方向垂直纸面向里.今有一带电粒子在A、B间竖直平面内做半径为R的匀速圆周运动.则带电粒子转动方向为_________时针方向,速率υ=_________.
图—20
8、电子自静止开始经M、N板间(两板间的电压为u)的电场加速后从A点垂直于磁场边界射入宽度为d的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求匀强磁场的磁感应强度.(已知电子的质量为m,电量为e)
9、已经知道,反粒子与正粒子有相同的质量,却带有等量的异号电荷.物理学家推测,既然有反粒子存在,就可能有由反粒子组成的反物质存在.1998年6月,我国科学家研制的阿尔法磁谱仪由“发现号”航天飞机搭载升空,寻找宇宙中反物质存在的证据.磁谱仪的核心部分如图所示,PQ、MN是两个平行板,它们之间存在匀强磁场区,磁场方向与两板平行.宇宙射线中的各种粒子从板PQ中央的小孔O垂直PQ进入匀强磁场区,在磁场中发生偏转,并打在附有感光底片的板MN上,留下痕迹.假设宇宙射线中存在氢核、反氢核、氦核、反氦核四种粒子,它们以相同速度v从小孔O垂直PQ板进入磁谱仪的磁场区,并打在感光底片上的a、b、c、d四点,已知氢核质量为m,电荷量为e,PQ与MN间的距离为L,磁场的磁感应强度为B.
(1)指出a、b、c、d四点分别是由哪种粒子留下的痕迹 (不要求写出判断过程)
(2)求出氢核在磁场中运动的轨道半径;
(3)反氢核在MN上留下的痕迹与氢核在MN上留下的痕迹之间的距离是多少
10、如图所示,在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸里,磁感应强度为B.一带负电的粒子(质量为m、电荷量为q)以速度v0从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.求:
(1)该粒子射出磁场的位置;
(2)该粒子在磁场中运动的时间.(粒子所受重力不计)
11、如图—23所示,套在足够长的固定绝
缘直棒上的小球,质量为10—4kg,带有4×10—4C
的正电,小球可沿棒滑动,动摩擦因数为0.2。把
此棒竖直地放在互相垂直且境外沿水平方向的匀
强电场和匀强磁场中,电场强度为10N/C,磁感
强度为0.5T.求小球由静止释放后下落过程中的最
大加速度和最大速度(g取10m/s2)
12、如图—24所示,在一坐标系内,x轴
上方有磁感强度为B的匀强磁场,下方有电场强
度为E的匀强电场。今有质量为m、电量为q的
带电粒子从y轴上某处静止释放后 恰能经过x
轴上的距原点O为l的P点,不计重力。
(1)粒子带的是什么电?
(2)释放点离原点O的距离应满足什么条件?
(3)从释放点到P点,粒子一共经历多长时间?
13.如图1-3-18所示, 磁感强度为B的均匀磁场中,固定放置一绝缘材料制成的边长为L的刚性等边三角形,其平面与磁场方向垂直,在DE边上的S点(DS=L/4)处带电粒子的放射源,发射粒子的方向皆在图中纸面内垂直DE边向下,发射粒子的电量皆为q(q>0),质量皆为m,但速度v有各种不同的数值,若这些粒子与框架的碰撞时均无能量损失,并要求每一次碰撞时速度方向垂直于被碰的边,试问
(1)带电粒子速度v取哪些值时可使S点发出的粒子最终又回到S点?
(2)这些粒子中,回到S点所用时间最短为多少?(重力不计,磁场范围足够大)
参 考 答 案
1、C 2、D 3、BD 4、A 5、BCD 6、(向右,6×104m/s) 7、(顺,BRg/E)
8、解析:电子在M、N间加速后获得的速度为v,由动能定理得:
mv2-0=eu
电子进入磁场后做匀速圆周运动,设其半径为r,则:
evB=m
电子在磁场中的轨迹如图,由几何得:
=
由以上三式得:B=
9、解:(1)a、b、c、d四点分别是反氢核、反氦核、氦核和氢核留下的痕迹.
(2)对氢核,在磁场中做匀速圆周运动,由牛顿第二定律得:
(3)由图中几何关系知:
所以反氢核与氢核留下的痕迹之间的距离
10、解:(1)带负电粒子射入磁场后,由于受到洛伦兹力的作用,粒子将沿图示的轨迹运动,从A点射出磁场,设O、A间的距离为L,射出时速度的大小仍为v,射出方向与x轴的夹角仍为θ,由洛伦兹力公式和牛顿定律可得:
qv0B=m 式中R为圆轨道半径,解得:
R= ①
圆轨道的圆心位于OA的中垂线上,由几何关系可得:
=Rsinθ ②
联解①②两式,得:L=
所以粒子离开磁场的位置坐标为(-,0)
(2)因为T==
所以粒子在磁场中运动的时间,t=
11、am=2m/s2,υm=5m/s
12、(1)负电
(2)d=qL2B2/(8Mek2) (K=1,2,3……)
(3)t=+ (K=1,2,3……)
13.(1)vn=(n=1,2,3…) (2) tmin =
F
E
D
S
图1-3-18
同课章节目录
- 第一章 电荷的相互作用
- 1.1静电现象与电荷守恒
- 1.2探究电荷相互作用规律
- 1.3静电与生活
- 第二章 电场与示波器
- 2.1探究电场的力的性质
- 2.2研究电场的能的性质( 一)
- 2.3研究电场的能的性质( 二)
- 2.4电容器 电容
- 2.5探究电子束在示波管中的运动
- 第三章 从电表电路到集成电路
- 3.1学会使用多用电表
- 3.2研究电流、电压和电阻
- 3.3探究电阻定律
- 3.4多表电表电路分析与设计
- 3.5逻辑电路与集成电路
- 第四章 探究闭合电路欧姆定律
- 4.1探究闭合电路欧姆定律
- 4.2测量电源的电动势和内阻
- 4.3典型案例分析
- 4.4电路中的能量转化与守恒
- 第五章 磁场与回旋加速器
- 5.1磁与人类文明
- 5.2怎样描述磁场
- 5.3探究电流周围的磁场
- 5.4探究安培力
- 5.5探究洛仑兹力
- 5.6洛仑兹力与现代科技
